Resistenze in serie e parallelo

Per lo schermo intero, “clic” su tasto destro e scegli.
Per avanzare con la presentazione, “frecce”.
Per chiudere, “esc”
Resistenze in serie e parallelo
di
Federico Barbarossa
Resistenze in serie
Nel circuito disegnato
sono inserite in serie le
resistenze R1 ed R2 .
Le resistenze sono in serie
quando:
1. disposte una di
seguito all'altra, sono
attraversate dalla stessa
corrente.
2. la tensione ai capi
della serie (AB) è uguale alla
somma delle tensioni sulle
singole resistenze:
∆V = ∆V1 + ∆V2 + .......
Resistenze in serie
ai capi (AB) della
serie delle due resistenze,
è quindi applicata una
certa tensione ∆V
La corrente che circola
nelle due resistenze è I.
Per la legge di Ohm la resistenza totale
(equivalente) è:
Resistenze in serie
Se a ∆V sostituiamo
∆V1 + ∆V2 otteniamo:
Possiamo quindi affermare che:
la resistenza equivalente di resistenze poste
in serie in un circuito, è uguale alla somma
delle resistenze stesse.
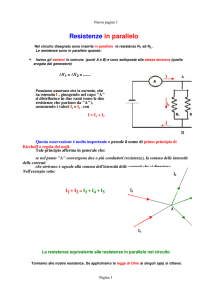
Resistenze in parallelo
Nel circuito
disegnato sono inserite in
parallelo le resistenze R1
ed R2 .
Resistenze in parallelo
le resistenze hanno gli
estremi in comune (punti
A e B)
e sono sottoposte alla stessa
tensione (quella erogata dal
generatore)
∆V1 = ∆V2
∆V1
∆V2
Resistenze in parallelo
Possiamo osservare che la
corrente, che ha intensità I
, giungendo nel capo "A" si
distribuisce in due rami (sono le
due resistenze che partono da
"A"), assumendo i valori I 1 e I 2 ,
con:
I = I 1 + I2
Resistenze in parallelo
Questa osservazione è molto
importante e prende il nome di
primo principio di Kirchhoff o
regola dei nodi.
Tale principio afferma in generale che:
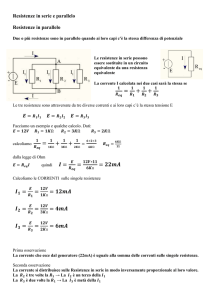
Resistenze in parallelo
Kirchhoff
Se nel punto "A" convergono due o
più conduttori (resistenze), la somma
delle intensità delle correnti che arrivano
è uguale alla somma dell'intensità delle
correnti che si dipartono.
Nell'esempio sotto:
I 1 + I2 = I3 + I4 + I 5
La Resistenze equivalente alle resistenze in
parallelo nel circuito
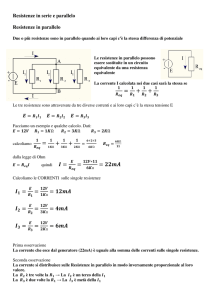
Torniamo alle nostre resistenze.
Se applichiamo la legge di Ohm ai
singoli rami si ottiene:
∆V = I1 · R1
∆V = I2 · R2
ricaviamo I1 e I2
se
raccogliamo ∆V …….
I1 + I2 = I
allora
…..e dividiamo tutto per ∆V
cioè
da cui, per un qualsiasi numero n di resistenze in parallelo,
resistenze in parallelo nel circuito
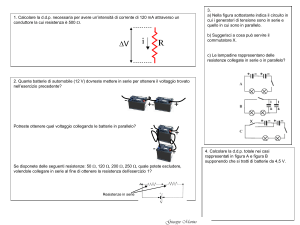
Svolgiamo questo esercizio:
R1 = 50 
R2 = 100 
in parallelo
Quanto vale la resistenza equivalente?
applichiamo
3
1
Se
=
R 100 
Allora
Resistenza equivalente
100
R
 33.3
3