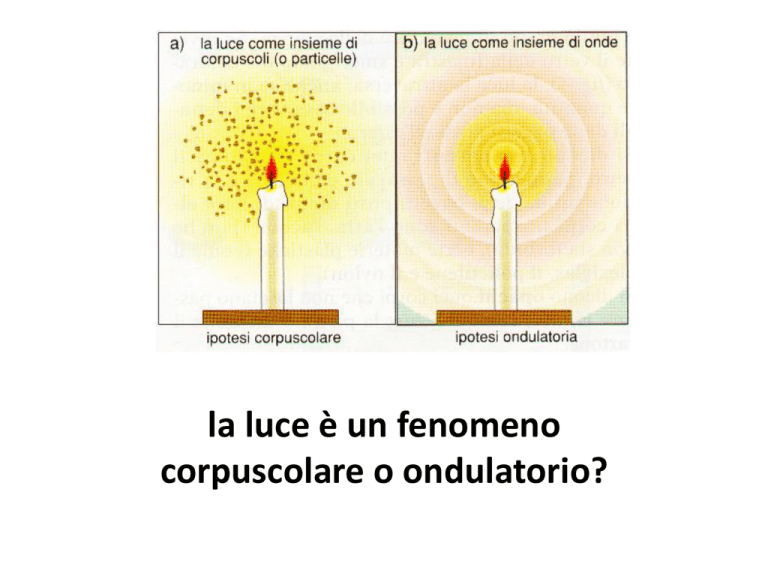
la luce è un fenomeno
corpuscolare o ondulatorio?
Nei primi dell ‘800, Young allestisce un’esperienza che sembra mettere fine
alla questione. (esperienza della doppia fenditura)
I fori, per diffrazione, si comportano come sorgenti della stessa luce.
I segnali luminosi uscenti subiscono interferenza, in fase e in opposizione di fase,
che porterà sullo schermo l’alternanza di bande chiare e scure,
Se la luce fosse fatta da particelle la loro interferenza non comporterebbe questo
risultato sullo schermo (bensì zone più chiare o più scure, ma in modo casuale)
Interferenza distruttiva
Interferenza Costruttiva
Un’onda marina è un’oscillazione di “forma” della massa
d’acqua.
Un’onda sonora è una variazione “volumetrica” della
massa del mezzo (compressione ed espansione).
Maxwell, nell’800, basandosi sulle le leggi fisiche fino ad allora scoperte, relativamente
all’elettricità e al magnetismo, dimostrò matematicamente che la luce è una
perturbazione (oscillazione) periodica di campo elettromagnetico che si propaga nello
spazio. Hertz costruì il primo circuito a corrente «oscillante» producendo onde radio.
Come onda, quindi, la luce ha:
Una lunghezza d’onda λ (spazio tra un’onda e la successiva)
Un Periodo T (tempo impiegato per percorrere λ)
Una frequenza d’onda ν (numero di onde passanti per un punto in un
secondo). ν=1/T
Una velocità C (circa 300,000 km/sec)
Le tre grandezze sono legate dalla
formula: C= λ ν
(Dalla formula del moto rettilineo
unoforme v=s/t, se consideriamo V=C,
s=λ e t=T C= λ/T, ma 1/T=ν
sostituendo C= λ ν)
Quanta energia c’è nella luce?
In che modo interagisce con la materia?
La materia interagisce con la luce: continuamente assorbe ed emette segnali luminosi. Già da
tempo era noto che lunghezze d’onda (colori) emesse ed assorbite erano collegati con la
temperatura dei corpi. Tuttavia i corpi reali non sono in grado di assorbire o emettere tutte le
lunghezze d’onde. Per lo studio «matematico» di questi fenomeni occorreva un corpo ideale…
Il Corpo nero
Corpo capace di assorbire ed emettere luce di
qualsiasi lunghezza d’onda (o frequenza).
Con una certa approssimazione tutti i materiali solidi,
liquidi e gassosi con alta densità si comportano da «corpi
neri». Una stella, essendo sostanzialmente allo stato
gassoso molto denso, si comporta come corpo nero
(emette radiazioni di tutte le lunghezze d’onda)
Dispositivo di Kirchhoff Emulatore di
corpo nero utilizzato per studiare in
laboratorio l’interazione Luce-Materia
Un corpo nero
Un faretto
Una stella
… una lampadina
La luce emesse da una qualsiasi sorgente possiede una determinata luminosità, o
«potenza luminosa», L. Essa è definita come la quantità di energia emessa nel tempo
dalla sorgente (E/t). La sua unità di misura è il watt (J/sec).
Uno strumento di rilevazione, però, non riesce a «raccogliere» tutta la luce emessa da una
sorgente più o meno puntiforme o sferica (come quella di una stella) che tende, invece, a
disperdersi in tutte le direzioni dello spazio.
Per tale motivo si definisce un’altra
grandezza, cioè «l’Intensità luminosa» I
che è la luminosità (o potenza luminosa)
per unità di superficie, (I=L/S=W/m2) ed
è quella che effettivamente uno
strumento può «rilevare» e,
eventualmente, misurare.
fotometro
Considerando la formula (I=L/S), l’intensità luminosa dipende direttamente dalla potenza
luminosa ed inversamente dalla superficie.
Ma di quale superficie di tratta?
Se la luce si diffonde in tutte le direzioni dello spazio,
l’energia emessa (quindi la potenza) si distribuisce su
tutta la superficie di una sfera.
Non solo: più la luce si allontana dalla sorgente, più
è la superficie sferica di distribuzione, quindi minore la
potenza per unità di superficie.
Dato che la superficie di una sfera è S=4πr2 la formula completa è
I=L/4πr2
Da questa formula si evince che l’intensità luminosa diminuisce con il quadrato della
distanza (per es. se la distanza si raddoppia, l’intensità diminuisce di 4 volte, se si
triplica di 9 volte ecc.).
Riflessione: confrontando «visivamente» le stelle, notiamo tra loro una differenza di
luminosità (rilevabile anche con un fotometro), ma non possiamo affermare che la più
luminosa sia effettivamente la più grande, in quanto potrebbe «apparirci» più luminosa solo
perché più «vicina».
Se, però, oltre a misurare l’intensità I, con opportuni metodi riusciamo a conoscere le
distanze r delle varie stelle osservate, potremo risalire alle loro potenze luminose L: in tal
modo il confronto ci fornirà informazioni reali sulle relative dimensioni.
I Legge del corpo nero
Le sperimentazioni condotte con il dispositivo di Kirchhoff (corpo nero) sulle
intensità luminose emesse dalla materia portò ad una prima legge
Legge di Stefan-Boltzman
La potenza irradiata per unità di superficie (I) da un corpo nero è
direttamente proporzionale alla quarta potenza della sua
temperatura assoluta (T)
I=σT4
I = energia irradiata al secondo per ogni cm2 di superficie
σ = costante di Stefan-Boltzman
Oltre a misurarne l’energia e la potenza, di un segnale luminoso è possibile
analizzarne le componenti «cromatiche» attraverso lo spettrofotometro.
Sorgente
Luminosa
(Solido, liquido,
gas denso)
Spettrofotometro
(Luce prodotta da corpo nero)
Sorgente
Luminosa
(Gas rarefatto)
Spettrofotometro
(Solido, liquido,
gas denso)
(Gas rarefatto,
freddo)
(Luce prodotta da un gas rarefatto)
(Luce prodotta da un corpo nero e
assorbita da un gas rarefatto)
Spettrofotometro
Portato all’equilibrio termico, un corpo nero emette luce in tutte le lunghezze
d’onda (spettro continuo), ma con intensità distribuita in modo gaussiano ed il
picco più alto (il colore predominante) dipendente inversamente dalla
temperatura. Per esempio a 5.000 K il corpo nero si «percepisce» sul giallo; a
20/3000K sul bianco-blu ecc.
II legge del corpo nero
Un corpo nero portato all’equilibrio termico, emette radiazioni elettromagnetiche in tutte
le lunghezze d’onda ma con potenza differente e distribuite in modo gaussiano.
I valori di intensità per ogni lunghezza d’onda, rappresentati su un diagramma cartesiano
portano a grafici di distribuzione come quelli in figura.
Come si nota, il grafico «a campana» cambia in base alla temperatura del corpo nero: a
temperature maggiori diventa più «alto» e più «stretto».
Wien, considerando la λ di picco
(quella più intensa) in funzione della
temperatura, ottenne una legge
empirica (legge di Wien)
T x λmax=b
(b=costante di Wien)
La lunghezza d’onda con maggior intensità (colore predominante) tende a «mascherare»
ai nostri occhi le altre componenti cromatiche. Per tal motivo, alla variazione di
temperatura d’incandescenza, vediamo cambiare il colore della luce emessa.
Quelle di Stefan-Boltzman e di Wien erano, e sono, solo leggi «empiriche», ovviamente
occorreva «spiegarle» con leggi fisico-matematiche.
La luce e i fenomeni luminosi in genere erano state ben descritte e spiegate dalle
leggi dell’elettromagnetismo di Maxwell, ma nel caso del comportamento del
corpo nero, queste stesse leggi non erano in grado di fornire spiegazioni
convincenti.
In particolare, l’applicazione delle funzioni matematiche di Maxwell non portavano a
risultati tali da giustificare i grafici di Wien.
Maxwell
I motivi dell’insuccesso della teoria di Maxwell erano essenzialmente due. Si era convinti che:
1) L’energia contenuta in un segnale luminoso fosse correlata solo all’intensità
2) L’energia luminosa potesse assumere qualsiasi valore (valori continui)
PLANCK
Planck, nel tentativo di «far quadrare i conti» fu portato a ipotizzare:
1) Che l’energia contenuta in un segnale luminoso dipendesse anche dalla frequenza
d’onda (dal colore)
2) Che l’energia totale contenuta in un segnale luminoso di una determinata frequenza
non potesse avere qualsiasi valore, ma doveva essere multiplo di un «pacchetto
minimo» (valore discreto) che è specifico per ogni frequenza.
I suoi calcoli matematici portarono ad una formula elegante E=hν.
La formula rappresenta il pacchetto minimo di energia (quantum) contenuto in un segnale
luminoso di frequenza ν, dove h=costante di Planck (detta anche quanto d’azione)
In altre parole, per avere l’emissione di un segnale luminoso di un certo colore (frequenza
d’onda ν ) è necessaria una quantità minima e definita di energia (quantum) che è
funzione della frequenza stessa E=hν
L’energia totale contenuta in un segnale monocromatico è sempre un multiplo intero n del
quantum specifico Etot=nhν
Einstein e Compton
Grazie allo studio dell’effetto fotoelettrico e dell’effetto Compton, i due fisici
rilevarono che un segnale luminoso può «urtare» particelle, come gli elettroni,
«cedendo a quest’ultimi» energia cinetica quantizzata (multipli del quantum hν
ipotizzato da Planck). Il fenomeno viene spiegato paragonando un segnale
luminoso ad «treno» di particelle (fotoni) dotate di quantità di moto (mv).
Sono le prove «certe» che la luce ha natura dualistica:
1.Ha proprietà ondulatorie, descritte dalla teoria classica di Maxwell
2.Ha proprietà particellari, descritte dalla teoria quantistica
Bohr
Un segnale luminoso emesso o assorbito da corpo nero (solido, liquido, gas
denso) presenta uno spettro continuo. Differenti sono gli spettri di un gas
rarefatto: sia quello di emissione che quello di assorbimento evidenziano la
presenza di righe.
Emissione
Corpo nero
Emissione
Gas
rarefatti
Righe di assorbimento da parte
dell’atmosfera esterna, rarefatta, del
sole. (Sole=corpo nero)
Bohr spiegò i risultati degli spettri proponendo il modello atomico quantistico
che, tra l’altro, permetteva di superare quello planetario di Rutherford (che
aveva incontrato non poche difficoltà per la teoria di Maxwell)
Assorbimento di energia quantizzata:
calore o elettricità o luce con
determinata frequenza.
Ritorno allo stato fondamentale con
emissione di un segnale luminoso
con determinata frequenza.
La serie di frequenze (righe di colore) emesse o assorbite è specifica di ogni specie
atomica in quanto collegate con i livelli di energia degli elettroni (configurazione
elettronica): l’analisi spettrale porta a identificare il gas specifico.
Stella Corpo nero
Rilevamento Intensità luminosa
•
•
Ipparco Magnitudo apparente (lineare)
Pogson Magnitudo apparente (logaritmica) e Magnitudo
Assoluta
Applicazione Leggi corpo nero
•
•
WienTemperatura superficiale di una stella
Stefan-Boltzman potenza irradiata di una stella
Applicazione Teoria quantistica
•
Bohr (Spettri) Composizione chimica superficiale di una
stella
Classificazioni di Harvard classi spettrali