Nessun titolo diapositiva

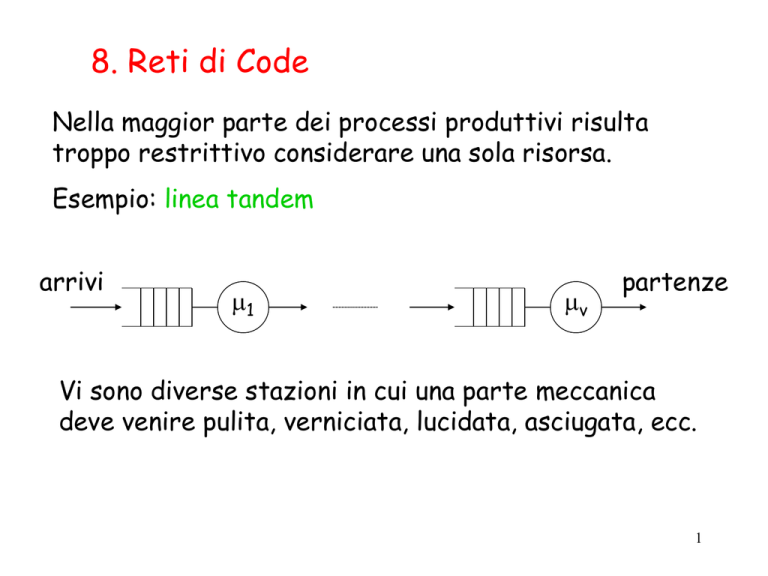
8. Reti di Code
Nella maggior parte dei processi produttivi risulta
troppo restrittivo considerare una sola risorsa.
Esempio: linea tandem
arrivi
1
v
partenze
Vi sono diverse stazioni in cui una parte meccanica
deve venire pulita, verniciata, lucidata, asciugata, ecc.
1
Esempio: linea con riciclo
arrivi
dall’esterno
1
2
partenze
riciclo
Vi sono due macchine in cascata. La prima esegue una
certa operazione e la seconda verifica che tale
operazione sia stata eseguita correttamente. Nel caso
in cui vi sia qualche imperfezione nella lavorazione,
questa deve essere eseguita nuovamente.
2
Le reti di code vengono distinte in
reti di code aperte
Vi sono arrivi dall’esterno e
vi sono parti che vengono
instradate al di fuori del
sistema.
reti di code chiuse
Il sistema è isolato: non
vi sono né arrivi
dall’esterno né parti che
vengono instradate al di
fuori del sistema.
3
Esempio: rete di code aperta
1
2
3
Esempio: rete di code chiusa
1
2
4
Come visto in precedenza la teoria delle code
consente di calcolare in modo sistematico le
grandezze caratteristiche a regime delle risorse
ergodiche nel caso in cui sia i tempi di inter-arrivo
che i tempi di servizio sono esponenziali.
Tali risultati non sono in genere applicabili alle reti
di code in cui gli arrivi in alcune risorse sono
strettamente legati alle uscite delle altre risorse e
non godono quindi necessariamente della proprietà
di markovianeità.
5
Esiste tuttavia un importante teorema relativo
alle code M/M/m che consente di utilizzare
nello studio delle reti di code M/M/m i risultati
visti in precedenza.
Teorema di Burke: In una risorsa M/M/m
ergodica e a regime, il processo di uscita è un
processo poissoniano caratterizzato dallo
stesso parametro del processo di ingresso.




6
Esempio: linea tandem a due stati con risorse M/M/1

1
2

La risorsa 2 vede in ingresso degli arrivi poissoniani
che sono l’uscita dalla risorsa 1.
Ogni singola risorsa può venire studiata
separatamente.
Numero medio di utenti nelle singole risorse a regime
ρ1
x1 
(1  ρ1 )
ρ2
x2 
(1  ρ2 )
7
Numero medio di utenti nella rete a regime
ρ1
ρ2
x  x1  x2 

(1  ρ1 ) (1  ρ2 )
Tempo medio di attraversamento della rete a regime
1
1
  1  2 

μ 1 (1  ρ1 ) μ 2 (1  ρ2 )
8
Reti di Code Markoviane Aperte
Sono costituite da v risorse M/M/m.
La i-esima risorsa ha tasso di servizio i e tasso di
ingresso complessivo i .
Il processo degli arrivi dall’esterno è poissoniano per
ciascuna risorsa. Indichiamo con iin quello relativo
alla i-esima risorsa.
All’uscita dalla i-esima risorsa il cliente viene
instradato alla risorsa j-esima con probabilità rij
oppure viene instradato all’esterno con probabilità ri0.
Chiaramente per ogni i, risulta
v
 rij  1
j 0
9
Esempio: rete aperta composta da tre risorse M/M/1
1
1in
v=3,
1
0.5
0.5
0.5
2
2in
1in = 2in = 7,
Valgono inoltre le
seguenti relazioni:
2
0.5
3
0.5
3
0.5
3in
3in = 14
λ 1  λ 1in  0.5 λ 3

in
λ

λ
 2
2  0.5 λ 1
λ 3  λ 3in  0.5 λ 2

10
In generale, data una rete aperta markoviana con
v risorse, possiamo scrivere v equazioni del tipo
λ i λ
in
i
v
  rji  λ j
j1
Equazioni di
traffico della rete.
Le probabilità rij vengono dette probabilità di
instradamento o di routing.
11
Introducendo i vettori riga
λ  λ 1  λ v
e definendo

in
λ in  λ 1
r11  r1v 

R
r
rvv 
 v1
 λv
in

Matrice di
routing
le equazioni di traffico possono essere riscritte in
forma matriciale come
λ  λ in  λ  R
12
da cui risulta che
λ λ in  (I  R) -1
Per quanto riguarda l’ergodicità di una rete aperta
vale il seguente
Teorema: Una rete aperta è ergodica se e solo se è
ergodica ogni singola risorsa.
Si dimostra che se una rete è ergodica la matrice
(I-R) è non singolare (condizione necessaria per
l’ergodicità della rete).
13
Essendo tale condizione solo necessaria, può aversi
che det(I-R)  0 senza che la rete sia ergodica.
Esempio

1
R  0
0 0
1
1 - 1
I - R  0
1 

2

det(I  R)  0
Tale sistema non è però ergodico per ogni valore di ,
1 e 2. Ad esempio non lo è se  > 1 oppure  > 2 .
14
Definiamo stato di una rete di code con v risorse, un
vettore riga x con v componenti, la cui i-esima
componente x(i) rappresenta il numero di utenti nella
i-esima risorsa.
x  x(1)  x(v)
La probabilità di stato di una rete di code è definita
come
Π(x1 , , xv )  Pr(x(1)  x1 , , x(v)  xv )
15
Teorema di Jackson: In una rete aperta di code
M/M/m, ergodica e a regime
1. la probabilità che vi siano xi utenti nella i-esima
risorsa può ricavarsi come se la risorsa fosse
isolata e avesse tasso di arrivo i, dove  i è
soluzione di
λ λ in  (I  R) -1
Πi si calcola
con le formule viste per le code isolate.
2. la probabilità che la rete sia nello stato
x  x1  xv 
è
Π(x1 , , xv )  Π1 (x1 )  Πv (xv )
16
Le risorse sono pertanto stocasticamente
indipendenti.
Si dice anche che le reti di code M/M/m aperte ed
ergodiche godono della forma prodotto.
Se una rete è ergodica
vale ancora la Legge di Little
17
Legge di Little in grande
Sia in il tasso medio degli arrivi a regime nella rete e
iin il tasso medio degli arrivi a regime nella i-esima
risorsa
v
in
in
λ  λi
i1
Sia x il numero medio di utenti a regime nella rete e xi
il numero medio di utenti a regime nella i-esima risorsa
v
x   xi
i1
x  λ in 
dove  indica il tempo medio di attraversamento
dell’intera rete di code.
18
Esempio: rete aperta composta da tre risorse M/M/1
1
1
1in
0.5
0.5
0.5
2
2
2in
1in = 2in = 7,
 0 0.5 0 
R 0
0 0.5
0 
0.5 0
0.5
3
0.5
3
0.5
3in
3in = 14
8/7 4/7 2/7 
(I - R)  2/7 8/7 4/7 
4/7 2/7 8/7 
-1
λ  18 16 22
19
Siano
1 = 20,
2 = 32,
allora 1 = 9/10,
3 = 33
2 = 1/2,
3 = 2/3.
Inoltre
Π(x1 , x2 , x3 )  Π1 (x1 )  Π2 (x2 )  Πv (xv )
e poiché vale la forma prodotto
x1
x2
Π(x1 , x2, x3 )  (1  ρ1 )ρ1  (1  ρ2 )ρ2  (1  ρ3 )ρ3
x3
20
ρ3
ρ1
ρ2
x  x1  x2  x3 


 12
(1  ρ1 ) (1  ρ2 ) (1  ρ3 )
1in = 1in + 2in + 3in = 7 + 7 + 14 = 28
 
x
12

λ in 28
Tempo medio di
attraversamento dell’intera
rete.
21
Reti di Code Markoviane Chiuse
Non vi sono arrivi dall’esterno, pertanto iin = 0, per
ogni i = 1, … , v.
Non vi sono partenze verso l’esterno, ossia ri0 = 0, per
ogni i = 1, … , v.
Il numero di clienti all’interno del sistema rimane
costante.
Lo spazio di stato di una rete chiusa con v risorse e n
utenti è finito e si denota con N v,n.
22
Esempio: v=2, n=3.
N v,n = { (3,0), (2,1), (1,2), (0,3) }
(v  n  1)!
v

n

1


card(N v,n)   n  

 n! (v  1)!
4!
card(N 2,3) 
4
3! 1!
23
Studiando le reti di code aperte Markoviane abbiamo
visto che, se queste sono ergodiche, possono essere
studiate esaminando le singole risorse singolarmente
poiché in virtù del teorema di Jackson le singole
risorse sono stocasticamente indipendenti.
Nelle reti chiuse invece questo non è più vero e le
risorse non sono più indipendenti. Infatti:
v
 xi  n
i1
ossia il numero di utenti nella
rete è costante.
24
Una possibilità per studiare una rete di code
Markoviane chiuse consiste nell’associare ad essa
una particolare catena di Markov a tempo continuo.
Sia
x  [ x1  xk  xj  xv ]
il generico stato della rete.
Costruiamo un grafo con tanti vertici quanti sono gli
stati della rete.
[ x1  xk  1  xj  1  xv ]
k rkj
[ x1  xk  xj  xv ]
25
La frequenza con cui un utente passa dalla k-esima alla
j-esima risorsa è pari a
k rkj
dove
• rkj rappresenta la probabilità che un utente che
esce dalla k-esima risorsa vada alla j-esima,
• k rappresenta il tasso delle partenze dalla
k-esima risorsa quando in essa vi sono xk utenti.
26
Esempio
1-p
1
v=2, n=3
2
card(N
2,3)
p
4
La rete può trovarsi in 4
diversi stati.
La prima risorsa ha un solo servente, la seconda
ne ha 2 (m1=1, m2=2).
27
x1
Catena di Markov
associata alla rete di
code chiusa
1
3,0
p 2
1
x4
2,1
x2
1
2 p 2
0,3
1,2
2 p 2
x3
Poiché il grafo associato a tale CMTC ammette
un’unica componente ergodica possiamo concludere
che la rete è ergodica.
Nello studio di questa rete possiamo quindi applicare i
risultati visti per le CMTC.
28
Sia 1 = 10, 2 = 6, p = 0.5
0 
 10 10 0
 13 0 10 
Q 3
6 10 - 16
 0
0
6 6
 0
Πl Q  0
 Π  1
 i l,i
27
Πl  
517
90
517
150
517
250 
517 
Distribuzione limite
29
Alternativamente possiamo basarci sulle equazioni di
traffico della rete:
v
λ i   rji  λ j
j1
che in forma matriciale possono essere scritte come
λ  λ R
dove R è la matrice di
routing che gode della
seguente proprietà
La matrice R associata ad una rete di code
chiusa ha sempre un autovalore = 1.
30
Teorema: Una rete di code markoviane chiusa è
ergodica se e solo se:
• l’autovalore = 1 di R è semplice.
Questo teorema è molto importante perché ci
permette di stabilire se una rete è ergodica
semplicemente calcolando gli autovalori della
matrice R che ha dimensioni pari al numero di
risorse.
Se invece associamo alla rete una CMTC e
applichiamo il criterio degli autovalori dobbiamo
determinare gli autovalori di Q che ha dimensioni
pari al numero di stati.
31
Esempio
1-p
1
1 
R  0
 p 1 - p
R -λ I  -pλ

2
p
1 
1 - p -λ 
det(R -λ I)  (λ - 1)(λ  p)
λ 1,2 
1
p
sempre ergodica
32
Vediamo ora come calcolare le probabilità di stato a
regime utilizzando le equazioni di traffico della rete.
Diamo prima le seguenti definizioni preliminari.
• Sia λ~ soluzione di λ  λ  R
λ~i
ρi 
μi
i  1, , v
coefficiente di traffico della i-esima risorsa
• i(xi) è una funzione che dipende dal numero di
serventi della i-esima risorsa
33
 Se la i-esima risorsa è a servente singolo
β i (xi )  ρixi
 Se la i-esima risorsa ha mi serventi
 ρixi
 x!

β i (xi )   i xi
 ρi
mi! mixi mi
se xi  mi
se xi  mi
34
Teorema di Gordon e Newell: In una rete di code
markoviane chiusa ed ergodica, la distribuzione di
probabilità di stato a regime è
1 v
Π(x1 , x2 , , xv )   Πβ i (xi )
C i1
dove C è una costante di normalizzazione
che si determina imponendo che

[x1 ,x2 ,,xv ]Nv,n
Π(x1 , x2 , , xv )  1
35
Osservazioni
1) La probabilità di stato a regime è anche nel caso
delle reti chiuse nella forma prodotto.
Tuttavia in questo caso le variabili di stato aleatorie
xi non sono indipendenti e quindi non è possibile
scrivere la probabilità come prodotto delle v
probabilità marginali.
2) La determinazione della costante di
normalizzazione C richiede l’enumerazione di tutti i
possibili stati della rete e risulta pertanto non
agevole poiché la cardinalità dello spazio di stato
risulta molto elevata anche per piccoli valori di n e v.
36
Esempio
1-p
1
2
p
Sia n=3, 1 = 10, 2 = 6, p = 0.5.
1  0
1 
R  0
 p 1 - p 0.5 0.5
1
ρ1 
10
1
λ~  2
 
1
ρ2 
3
37
β 1 (x1 )  ρ1
x1
 ρ2 x2
 x2
β 2 (x2 )   ρ2
2x2 1
se x2  2
se x2  2
β 1 (0)  1 β 1 (1)  1/10 β 1 (2)  1/100 β 1 (3)  1/1000
β 2 (0)  1 β 2 (1)  1/3 β 3 (2)  1/18 β 2 (3)  1/108
β1 (3) β2 (0)
1
β1 (2) β2 (1)
1
Π(3,0) 

Π(2,1) 

C
1000C
C
300C
β1 (1) β2 (2)
1
β1 (0) β2 (3)
1
Π(1,2) 

Π(0,3) 

C
180C
C
108C
38
Π(3,0)  Π(2,1)  Π(1,2)  Π(0,3)  1
156
C
8147
 Π(3,0)  27

517


 Π(2,1)  90
517



150
 Π(1,2)  517


Π(0,3)  250

517
Tale distribuzione
coincide con quella
trovata associando
una CMTC alla rete.
39