teoria errori

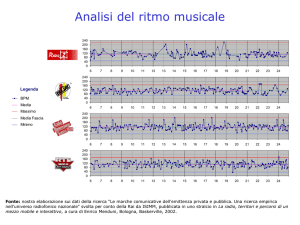
Teoria degli errori
Distribuzione empirica degli errori
N misure di una grandezza 1-dim X a valori reali
(N molto grande)
n
X
Istogramma delle misure
(nell’i-esimo intervallino ni misure,
n
i
N )
x
N
1
N
s X2 
sX
x
media empirica
(vicino al centro dell’istogramma)
i
N
1
N
2
(
x

x
)
 i
varianza empirica
scarto quadratico medio empirico
(indice della dispersione)
Modello probabilistico di previsione
X variabile aleatoria
fX
f
I
X
densità di probabilità
( x)dx  probX  I 

f
X
( x)dx  1

(notazione:
)
Media empirica e valore atteso
(stesso legame fra varianza empirica e varianza)
Gaussiana
= valore atteso
= scarto quadratico medio
Correlazioni
N misure di una coppia di grandezze
 i( j )  xi( j )  x ( j ) , i  1,, N , j  1,2
medie empiriche
grande in val.ass. se  i(1) ,  i( 2 )
hanno prevalentemente
segni concordi, oppure
segni discordi
coefficiente di correlazione
empirico
Variabile aleatoria 2-dim
densità di probabilità congiunta
( def.:
In notazione matriciale
definita positiva
)
indipendenti:

Gaussiana congiunta:
= valore atteso
C diagonale
C = matrice di covarianza


indipendenti
Propagazione degli errori

Esempio:
N misure con

APPENDICE
Propagazione dell’errore: esempio elementare