Energia Potenziale Elettrica e Potenziale elettrico
La forza di Coulomb, mattone di tutta l’elettrostatica, è una forza conservativa. E’
quindi possibile definire per essa una funzione Energia Potenziale.
• L’energia potenziale è la funzione U(x,y,z), definita in ogni punto P(x,y,z) dello
spazio, che dà il lavoro necessario per portare una carica q0 da un punto
di riferimento precedentemente determinato al punto P, cambiato di segno.
• Come per ogni forza conservativa il calcolo del lavoro non dipende dalla
traiettoria che viene percorsa.
• Le proprietà dell’energia potenziale elettrica saranno le medesime di quella
gravitazionale già trovata in meccanica
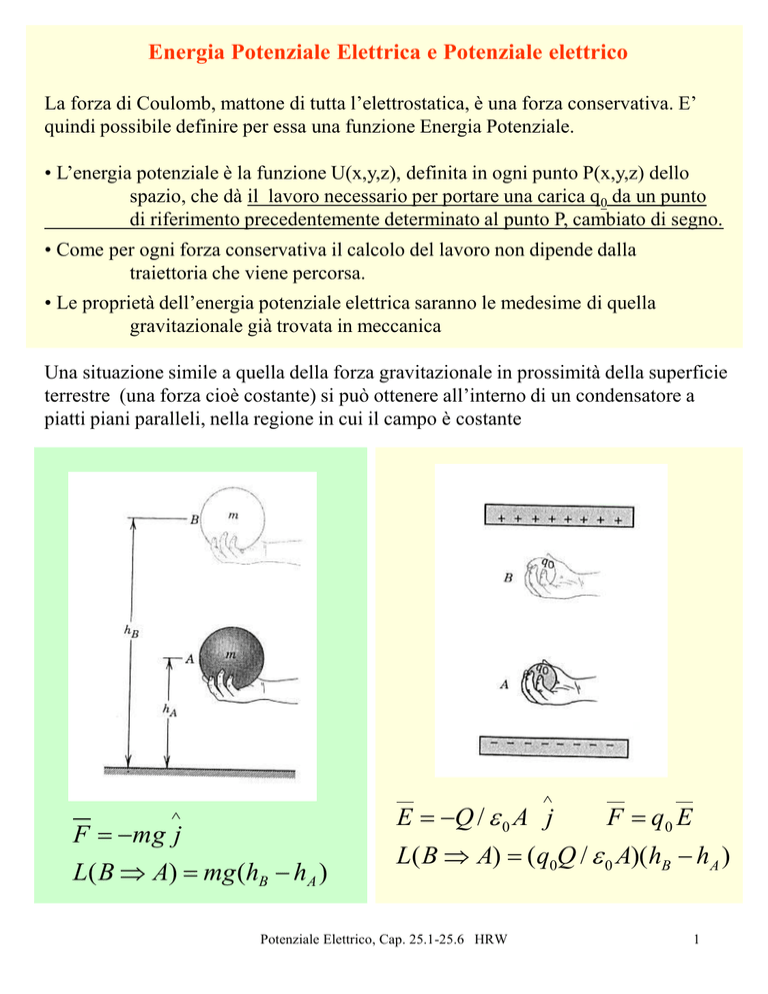
Una situazione simile a quella della forza gravitazionale in prossimità della superficie
terrestre (una forza cioè costante) si può ottenere all’interno di un condensatore a
piatti piani paralleli, nella regione in cui il campo è costante
E Q / 0 A j
F mg j
L( B A) mg (hB hA )
F q0 E
L( B A) (q0Q / 0 A)( hB hA )
Potenziale Elettrico, Cap. 25.1-25.6 HRW
1
Energia potenziale per una carica puntiforme
L’energia potenziale posseduta da una carica puntiforme q0 nel punto A (xA,yA,zA)
immersa in un campo elettrico generato dalla carica puntiforme Q è dato dal lavoro
necessario portare la carica da A ad un punto di riferimento P
U ( A) F ds
l
l
1 Qq0
r ds
40 r 2
Poiché il lavoro non dipende dalla traiettoria posso
scegliere una traiettoria ‘facile’ per andare da A a P
Q
A(xA,yA,zA)
q0
1) Mi muovo su un arco di circonferenza di
centro in Q da A al punto B
Poiché lo spostamento è ortogonale
alla forza (radiale) il lavoro è nullo
2) Mi muovo in direzione radiale da B a P
U ( A)
B
q0
P(xrif,yrif,zrif)
1 Qq 0
dr
2
4
r
0
A P
1 1
1 Qq0
1
1
1
1
1
U ( A)
dr
Qq
dr
Qq
Qq
0
0
0
2
2
r
4
r
4
r
4
4
B
0
0
0
0
rB rP
A P
B P
1 1
1 1
1
1
U ( A)
Qq0
Qq0
40
rA rP 40
rA rrif
P
Se considero il punto di riferimento all’infinito. Il potenziale di una carica puntiforme
q0 posta nel punto A all’interno del campo elettrico generato dalla carica Q distante da
q0 rA è dato da:
U ( A)
1 Qq0
40 rA
Potenziale Elettrico, Cap. 25.1-25.6 HRW
2
Potenziale
Si definisce potenziale del punto A, V(A) il rapporto dell’energia potenziale con il
valore della carica sonda q0.
V ( A)
V J Volt
C
U ( A)
F ds
E ds
q0
q0
a rif
rif A
E lo stesso approccio con cui si è passati dalla forza al campo elettrico si elimina
cioè la carica prova e si crea una funzione che dipende solo dalla sorgente del
campo.
Nel caso in cui Q è una sorgente puntiforme allora
V ( A) V (Q, rA )
1 Q
40 rA
Il potenziale è associato unicamente alla distribuzione di carica che genera il
campo elettrico. Il potenziale di una carica puntiforme costituisce il mattone con
cui, con un processo di integrazione, si costruisce il potenziale di una qualsiasi
distribuzione di cariche
r
P(x0,y0,z0)
V ( x0 , y0 , z0 )
( x, y, z ) dV
1
4
vol
0
r
( x, y, z ) Densità di carica in x, y, z
Potenziale Elettrico, Cap. 25.1-25.6 HRW
3
Come è possibile passare dal campo elettrico al potenziale (con un processo di
integrazione nello spazio) è anche possibile ritornare indietro, passare cioè dal
potenziale al campo elettrico. Il procedimento matematico è quello, ovviamente, di
derivazione.
Tuttavia:
Il potenziale è uno scalare il campo elettrico è un vettore.
Il passaggio da campo elettrico a potenziale è stato fatto mediante un prodotto
scalare. Dal potenziale dobbiamo recuperare tutte e tre le componenti di E.
L’operatore matematico in grado di fare questo procedimento inverso è il gradiente
indicato come o come Grad.
V
V
V
x
r
r
V
1 V
1 V
E V
y
r
r
V V
V
1
z
r sin z
Le componenti del campo elettrico si ottengono a partire dal potenziale come la
derivata parziale del potenziale rispetto alla variabile stessa cambiata di segno.
In dipendenza dal sistema di coordinate usato la derivata parziale può avere o meno
un coefficiente moltiplicativo.
In generale per descrivere un sistema di cariche più che la forza o il campo
elettrico si usa il potenziale. Infatti:
• Il potenziale è uno scalare (ho cioè una sola componete, invece che tre)
• Mediante il gradiente è facile passare dal potenziale al campo
• Il potenziale mi permette il calcolo del lavoro, che in generale è
l’osservabile che serve nei problemi pratici
Potenziale Elettrico, Cap. 25.1-25.6 HRW
4
Potenziale di una carica puntiforme
E’data una carica puntiforme Q posta
nell’origine del sistema di coordinate
sferiche. Il potenziale generato da
questa carica nel punto A posto ad una
distanza radiale rA è dato da:
V ( A) V (Q, rA )
1 Q
40 rA
L’andamento del potenziale V in
funzione della distanza radiale è di tipo
iperbolico.
Passando dalla posizione A alla posizione B (avvicinandosi quindi a Q carica
sorgente del campo) una carica qualsiasi q0 passa da una regione a potenziale più
basso ad una regione a potenziale più alto. Il lavoro che dovrà essere compiuto è pari
a:
L q0 V ( B) V ( A) q0 V (Q, rA ) V (Q, rB )
L q0
Q 1 1
40 rA rB
E’ cioè positivo per una carica positiva e negativo per una carica negativa
Una carica positiva, se lasciata libera di muoversi, accelererà da una regione di
potenziale maggiore verso una regione a potenziale minore
• rotola giù dalla curva
Una carica negativa, se lasciata libera di muoversi, accelererà da una regione di
potenziale minore verso una regione a potenziale maggiore
Ovviamente non cambia assolutamente nulla per un campo elettrico generato da una
carica -Q basta solo invertire i segni
Potenziale Elettrico, Cap. 25.1-25.6 HRW
5
Superfici Equipotenziali
Una superficie equipotenziale è una superficie dello spazio 3D su cui il
potenziale elettrico è lo stesso in ogni punto.
Nel caso di un campo elettrico generato
da una carica puntiforme le superfici
equipotenziali sono delle sfere.
1 Q
costante
40 r
r costante
V (Q, r )
In caso di distribuzione
di cariche più
complesse le superfici
equipotenziali possono
assumere forme piu
complicate
Nota:
Non si deve compiere lavoro per muovere una carica su una superficie equipotenziale
L’intensità del campo elettrico generato da una qualsiasi distribuzione di cariche è
sempre perpendicolare alle superfici equipotenziali ed è orientata nel verso del
potenziale crescente
Potenziale Elettrico, Cap. 25.1-25.6 HRW
6
Obiettivi generali degli esercizi (aula/tutor.):
Saper calcolare il potenziale dovuto ad una carica e
comprendere e saper utilizzare il principio di sovrapposizione;
Saper calcolare il lavoro nota la ddp e saper applicare
la conservazione dell’energia per l’elettrostatica.
Nota:
Anche questi argomenti trattati esclusivamente in Aula sono
argomento di esame
Potenziale Elettrico, Cap. 25.1-25.6 HRW
7












