Congruenza di triangoli
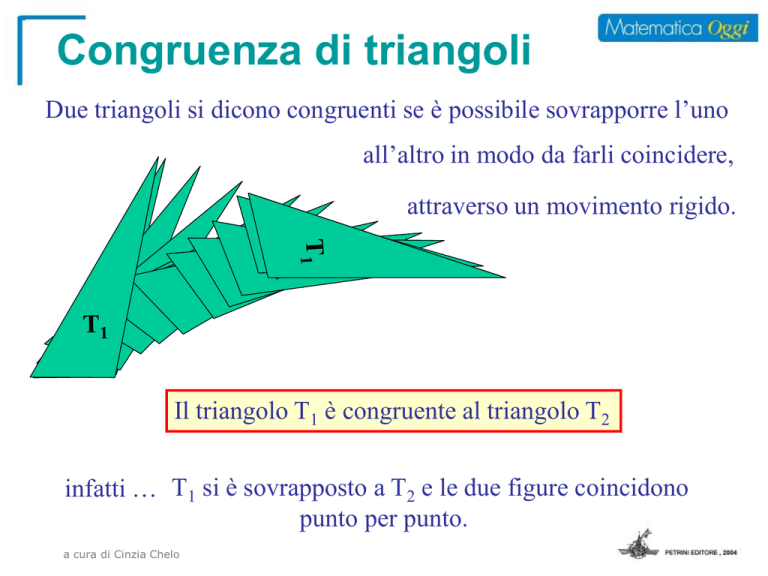
Due triangoli si dicono congruenti se è possibile sovrapporre l’uno
all’altro in modo da farli coincidere,
attraverso un movimento rigido.
T2
T11
T
Il triangolo T1 è congruente al triangolo T2
infatti … T1 si è sovrapposto a T2 e le due figure coincidono
punto per punto.
a cura di Cinzia Chelo
In particolare risultano verificate
le seguenti congruenze:
C’
C
A’
B
A
B’
A =A’
B =B’
C =C’
AB = A’B’
BC = B’C’
AC = A’C’
Due triangoli congruenti hanno i tre angoli e i tre lati congruenti
Viceversa …
Se due triangoli hanno i tre lati e i tre angoli rispettivamente
congruenti allora sono congruenti.
Per verificare la congruenza tra due triangoli ABC e A’B’C’,
non è però necessario verificare tutte e sei le condizioni.
Esistono infatti:
I CRITERI DI CONGRUENZA
Sono delle scorciatoie per stabilire se due triangoli sono congruenti,
Per appurare la congruenza tra due triangoli ABC e A’B’C’,
non è necessario verificare tutte e sei le condizioni:
A = A’
B = B’
C = C’
AB = A’B’
BC = B’C’
AC = A’C’
E’ sufficiente verificarne solo tre, ma
ATTENZIONE!
non tre qualsiasi …
… SOLO QUELLE ESPRESSE NEI TRE CRITERI
I tre criteri di congruenza dei triangoli
• Primo criterio: Due triangoli sono congruenti se hanno
rispettivamente congruenti due lati e l’angolo compreso
• Secondo criterio: Due triangoli sono congruenti se
hanno rispettivamente congruenti un lato e i due angoli
ad esso adiacenti.
• Terzo criterio: Due triangoli sono congruenti se
hanno rispettivamente congruenti i tre lati.
Considerazioni sul primo criterio:
Primo criterio di congruenza:
Due triangoli sono congruenti se hanno rispettivamente congruenti
due lati e l’angolo compreso.
Perché proprio l’angolo compreso?
Se l’angolo congruente non è quello compreso…
i due triangoli non sono ugualmente congruenti?
Vediamo alcuni esempi per comprendere bene
e chiarire ogni dubbio:
Osserva questi triangoli …
V
R
P
Q
S
T
Essi hanno due lati e un angolo rispettivamente congruenti,
ma l’angolo compreso non è quello compreso fra i due lati;
PRQ = SVT
Due triangoli sono congruenti se hanno rispettivamente congruenti
due lati e l’angolo compreso tra i due lati.
PRQ = SVT
Se non sei ancora convinto, verifichiamo graficamente…
Prendiamo la riga e incominciamo a disegnare un segmento AB
D
Tracciamo una semiretta di origine A.
Quindi con apertura di compasso
a piacere puntiamo in B e
disegnamo una circonferenza.
La circonferenza interseca la
semiretta in due punti: C e D
C
A
B
Consideriamo il triangolo ABC
e il triangolo ABD
Essi hanno:
la stessa base AB
BC = BD per costruzione
lo stesso angolo A
Eppure, come appare evidente:
non sono congruenti !
FINE
a cura di Cinzia Chelo