Istituto Statale di Istruzione Secondaria
Pier Luigi Nervi
Lentini
Prof. Leonardo Brunetto
Lavoro realizzato da:
Almirante Salvatore
Castiglia Giuseppe
Spina Andrea
Teorema di Pitagora
Teorema di Euclide
Teorema di Pitagora
Il teorema di Pitagora è un teorema della geometria euclidea
che stabilisce una relazione fondamentale tra i lati di un
triangolo rettangolo.
Quello che modernamente
conosciamo come teorema di Pitagora
viene solitamente attribuito al filosofo
e matematico Pitagora. In realtà il suo
enunciato (ma non la sua
dimostrazione) era già noto ai
babilonesi, ed era conosciuto anche in
Cina e forse in India. La
dimostrazione del teorema è invece
con ogni probabilità successiva a
Pitagora.
La somma
delle aree dei
due quadrati
costruiti sui
cateti è
equivalente
all'area del
quadrato
costruito
sull'ipotenusa.
Dimostrazione algebrica
Dato un triangolo rettangolo di lati a, b e c, ed
indicando con c la sua ipotenusa e con a e b i
suoi cateti, il teorema è espresso
dall'equazione:
o, in alternativa, risolvendolo per c:
Da cui si ricavano i rispettivi cateti:
e
Se la terna a,b,c è costituita da numeri interi
essa si chiama terna pitagorica.
Inversamente, ogni triangolo in cui i tre lati
verificano questa proprietà è rettangolo: questo
teorema, con la sua dimostrazione, appare
negli Elementi immediatamente dopo il
teorema di Pitagora stesso.
Dimostrazione grafica
Molte sono le “dimostrazioni grafiche” del teorema di Pitagora. Spesso sono un
felice connubio tra geometria e arte. Alcune sono molto efficaci per “vedere”
intuitivamente il teorema.
Dimostrazione antica
Dimostrazione di Bhaskara
Dimostrazione di Leonardo da Vinci
Dimostrazione di Airy
Dimostrazione di Perigal
Dimostrazione di Dekker
Dimostrazione di Floor van Lamoen
Ma vediamo quella più tradizionale…
Dimostrazione tradizionale:
In ogni triangolo rettangolo il quadrato costruito sull’ipotenusa è equivalente
alla somma dei quadrati costruiti sui cateti
Siano ACDE e CBFG i quadrati, rispettivamente del
cateto AC e del cateto CB; il punto M la proiezione del
punto C sull’ipotenusa.
Condotta la perpendicolare CM dal vertice C
all’ipotenusa AB, si prolunghi fino ad incontrare in M il
lato NL del quadrato costruito sull’ipotenusa.
Il segmento HM divide il quadrato ANLB in due
rettangoli ANMH, HMLB, che per il primo Teorema di
Euclide che dice che in ogni triangolo rettangolo il
quadrato di un cateto è equivalente al rettangolo
dell’ipotenusa e della proiezione del cateto sulla
ipotenusa; sono rispettivamente equivalenti ai due
quadrati ACDE, CBFG.
E poiché la somma dei due triangoli dà il quadrato
dell’ipotenusa, resta dimostrato che il quadrato
dell’ipotenusa è equivalente alla somma dei quadrati dei
due cateti.
Dimostrazione antica
E’ forse la dimostrazione più conosciuta. Il quadrato grande può essere formato o
dal quadrato costruito sull’ipotenusa e da quattro triangoli rettangoli uguali o dai
due quadrati costruiti sui cateti e da quattro triangoli rettangoli uguali.
Dimostrazione di Bhaskara
Questa bellissima dimostrazione è di Bhaskara (1114 - 1185), grande matematico e
astronomo indiano.
Dimostrazione di Leonardo da
Vinci
La dimostrazione di Leonardo è geniale. Le due figure sono divise dalle diagonali
verticali in parti uguali.
Dimostrazione di Airy
E’ probabilmente la più elegante
dimostrazione. Traslando i triangoli
rettangoli superiori, come indicato
dalle frecce, dal quadrato costruito
sull’ipotenusa si ottengono i quadrati
costruiti sui cateti. Sembra (da
“Il giardino di Archimede”) che questa
dimostrazione sia stata ideata da G. B.
Airy, astronomo dell’osservatorio di
Greenwich dal 1836 al 1881, intorno al
1855. Nella parte centrale della figura Airy
scrisse la poesia:
I am, as you may see,
a2 + b2 – ab.
When two triangles on me stand,
Square of hypothenuse is plann’d;
But if I stand on them instead,
The squares of both sides are read.
Dimostrazione di Perigal
Fu proposta nel 1873 da Henry Perigal, agente di cambio inglese. Il punto A è il centro
del quadrato.
Dimostrazione di Dekker
Fu pubblicata nel 1888 dallo scrittore olandese Edward Douwes Dekker con lo
pseudonimo di Multatuli.
Dimostrazione di Floor van
Lamoen
Questa elegante dimostrazione è di Floor van Lamoen, brillante matematico (e
atleta) olandese.
Pitagora nacque a Samo nel 572 a.C. La storia di Pitagora è avvolta nel
mistero, di lui sappiamo pochissimo e la maggior parte delle testimonianze
che lo riguardano sono di epoca più tarda.
Alcuni autori antichi o suoi contemporanei come Senofane, Eraclito ed
Erodoto ci danno testimonianze tali da far pensare alla effettiva esistenza
storica di Pitagora pur se inserita nella tradizione leggendaria.
Secondo queste fonti Pitagora nacque nell'isola di Samo nella prima metà
del VI secolo a.C. dove fu scolaro di Ferecide e Anassimandro subendone
l'influenza nel suo pensiero.
Da Samo Pitagora si trasferì nella Magna Grecia dove fondò a Crotone,
all'incirca nel 530 a.C., la sua scuola. Dei suoi presunti viaggi in Egitto e a
Babilonia, narrati dalla tradizione dossografica, non vi sono fonti certe e
sono ritenuti, almeno in parte, leggendari.
Sulla sua morte i resoconti dei biografi non coincidono: essendo scoppiata
una rivolta dei democratici contro il partito aristocratico pitagorico, la casa
dove si erano riuniti gli esponenti più importanti della setta fu incendiata. Si
salvarono solo Archippo e Liside che si rifugiò a Tebe. Secondo una
versione, Pitagora prima della sommossa si era già ritirato nel Metaponto
dove era morto. Secondo altri invece era casualmente assente alla riunione
nella casa incendiata e quindi riuscì a salvarsi fuggendo prima a Locri,
quindi a Taranto e da lì a Metaponto dove morì nel 495 a.C.
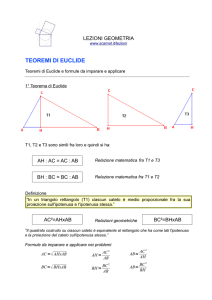
Teoremi di Euclide
Il primo teorema di Euclide è un teorema concernente il triangolo rettangolo che
deriva, assieme al secondo, dalla proposizione 8 del VI libro degli Elementi di Euclide;
nei testi scolastici può essere enunciato in due modi diversi a seconda della proprietà
che si desidera sottolineare:
•mediante l'equiestensione tra figure:
In un triangolo rettangolo il quadrato costruito su un cateto è equivalente al rettangolo
avente per dimensioni l'ipotenusa e la proiezione di quel cateto sull'ipotenusa stessa.
•mediante relazioni tra segmenti:
In un triangolo rettangolo il cateto è medio proporzionale tra l'ipotenusa e la proiezione
del cateto stesso sull'ipotenusa.
Le due enunciazioni sono equivalenti.
Il secondo teorema di Euclide è un teorema concernente il triangolo rettangolo che
deriva, assieme al primo, dalla proposizione 8 del VI libro degli Elementi di
Euclide; nei testi scolastici può essere enunciato in due modi diversi a seconda della
proprietà che si desidera sottolineare:
•mediante l'equiestensione tra figure:
In un triangolo rettangolo, il quadrato costruito sull'altezza relativa all'ipotenusa è
equivalente al rettangolo che ha per lati le proiezioni dei due cateti sull'ipotenusa.
•mediante relazioni tra segmenti:
In un triangolo rettangolo, l'altezza relativa all'ipotenusa è medio proporzionale tra le
proiezioni dei due cateti sull'ipotenusa.
Le due enunciazioni sono equivalenti
In un triangolo rettangolo il quadrato
costruito su un cateto è equivalente
al rettangolo avente per dimensioni
l'ipotenusa e la proiezione di quel
cateto sull'ipotenusa stessa. (Primo
teorema)
In un triangolo rettangolo, il
quadrato costruito sull'altezza
relativa all'ipotenusa è equivalente
al rettangolo avente per
dimensioni le proiezioni dei cateti
sull'ipotenusa. (Secondo teorema)
Della vita di Euclide (circa 365-300 a. C.) la sola notizia certa è che insegnò
geometria ad Alessandria d'Egitto, dove fondò una scuola di matematica.
Euclide è il più importante matematico dell'antichità, conosciuto soprattutto
per il suo trattato di geometria, gli Elementi (in greco Stocheia). E' composto
da 13 libri concernenti la geometria piana, le proporzioni, la teoria dei
numeri, le grandezze incommensurabili e la geometria solida. In quest'opera
viene proposta una riorganizzazione in forma deduttiva delle conoscenze
geometriche dell'epoca che divenne il fulcro dell'insegnamento della
matematica per duemila anni e il modello di strutturazione logica di ogni
branca del sapere scientifico.
Gli Elementi si aprono con la definizione di teoremi, assiomi e postulati. Gli
assiomi e i postulati sono indicati da Euclide come affermazioni di partenza
da cui far discendere tutte le altre con un procedimento dimostrativo. Mentre
gli assiomi indicano verità "evidenti" di carattere logico, i postulati hanno,
invece, carattere geometrico. Tra i postulati il quinto, detto "postulato delle
parallele", ha dato origine a molte controversie sulla possibilità o meno di
ricavarlo come teorema a partire dagli altri quattro.
A Euclide sono stati attribuiti anche i Dati, raccolta di teoremi in 95
proposizioni; i Fenomeni, una descrizione geometrica delle sfere celesti;
l'Ottica, un trattato di ottica geometrica.
Salvatore Almirante
Giuseppe Castiglia
Andrea Spina