Ciclo di Carnot

Ciclo di Carnot
Termodinamica
La termodinamica studia le trasformazioni e passaggi di
energia da un sistema ad un altro e da una forma all’altra,
ovvero la termodinamica si occupa di descrivere i
fenomeni di riscaldamento (fenomeni termici) e la loro
relazione con i fenomeni meccanici. Più in generale studia i
fenomeni termici in relazione ad altre forme di energia,
cioè lo studio dei meccanismi (lavoro di forze d’attrito,
reazioni chimiche, passaggio di corrente elettrica, …)
attraverso i quali lo stato di un sistema macroscopico può
essere fatto variare.
Termodinamica
Gli scambi energetici tra un sistema (un gas che si
trova all’interno di un cilindro) e l’ambiente
circostante possono avvenire, in senso generale,
mediante lo scambio di calore, Q, e di lavoro
meccanico, L.
Il primo principio della termodinamica è il principio
di conservazione dell’energia e non pone limiti al
verso di scambio energetico tra il sistema e l’ambiente
circostante.
Termodinamica
In linea di principio, cioè avendo a disposizione solo le
indicazioni del primo principio, si possono avere le
seguenti due situazioni:
1) Tutto il lavoro, L, meccanico può essere trasformato
tutto in calore, Q.
L  Q
2) Tutto il calore, Q, può essere trasformato tutto in lavoro
meccanico:
Q  L
Termodinamica
In natura, però, si osservano cose diverse.
Mentre è possibile tutto il lavoro in calore, ad esempio nei
fenomeni in cui è coinvolto l’attrito, non è possibile
trasformare tutto il calore in lavoro.
Quindi in natura non vi simmetria nei processi di scambi di
energia tra un sistema e l’ambiente circostante.
Tale simmetria è stato formalizzato nel secondo principio
della termodinamica.
Secondo principio della Termodinamica
Ta
Qa
M
L
Tb
Esistono
due,
classiche,
formulazioni
del
secondo
principio della termodinamica.
Enunciato di Kelvin – Planck:
Non è possibile costruire una
macchina termica che esegue un
ciclo termico il cui unico
risultato è quello di assorbire
calore da una sola sorgente e di
trasformarlo tutto in lavoro
meccanico.
Macchina non possibile!
Secondo principio della Termodinamica
Ta
Qc
M
Qa
Tb
Enunciato di Clausius: Non è
possibile costruire una macchina
termica che esegue un ciclo
termico il cui unico risultato è
quello di trasferire calore da una
sorgente fredda ad una calda senza
fornire alla macchina energia sotto
forma di lavoro meccanico.
Cioè il calore non fluisce
spontaneamente da una sorgente
fredda ad una sorgente calda.
Macchina termica non possibile!
Macchina termica
La macchina termica è un dispositivo che assorbe calore,
Qa, e, mediante una serie di trasformazioni
termodinamiche cicliche, trasforma una parte del calore
assorbito in lavoro meccanico, L, mentre la parte di calore
rimanente viene ceduta all’ambiente circostante.
Macchina termica
Uno schema di macchina termica è il seguente.
Ta
Qa
M
Tb
L
Qc
M = Macchina termica
Ta = Temperatura della sorgente
calda.
Qa = Calore fornita dalla
sorgente calda e assorbita dalla
macchina.
Tc = Temperatura della sorgente
fredda.
Qc = Calore fornita dala
sorgente fredda e ceduta dalla
macchina.
L = Lavoro fatto dalla
macchina.
Macchina termica
Il rendimento, , di una macchina termica è:
L Totale
Ta

Q assorbito
Qa
M
Tb
Q assorbitoQ ceduto

Q assorbito
L
Qc
Poiché il calore assorbito è
positivo, mentre il calore
ceduto è negativo, allora il
rendimento è:

Qassorbito  Qceduto
Qassorbito
1
Macchina termica
Poiché una macchina termica non può funzionare con una
sola sorgente di calore, senza violare il secondo principio
nell’enunciato di Kelvin-Planck, allora essa come minimo
deve utilizzare due sorgenti di calore.
Un indice di bontà di una macchina termica è il
rendimento termico, il cui valore è sempre più piccolo
dell’unità. Allora si pone il problema di costruire una
macchina che abbia il massimo rendimento possibile.
La risoluzione fu data, negli anni venti dell’ottocento,
dallo scienziato francese Sadi Carnot.
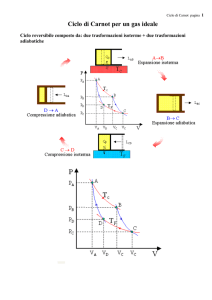
Ciclo di Carnot
Sadi Carnot ipotizzò la costruzione di una macchina
termica funzionante con due sole sorgenti di calore. Il
conseguente ciclo termico è costruito mediante quattro
trasformazioni termodinamiche: due isoterme e due
adiabatiche.
Nell’analisi del ciclo di Carnot le trasformazioni
termodinamiche sono trasformazioni reversibili.
Ciclo di Carnot - Analisi
Si prende in considerazione un cilindro contenete un gas perfetto,
però in senso generale si potrebbe usare un qualsiasi fluido.
Condizioni iniziali
All’inizio del ciclo il gas si trova nello stato
A descritto dalle grandezze macroscopiche
pressione, volume e temperatura:
PA = pressione
VA = volume
TA = Ta = temperatura della sorgente calda.
Nella figura è rappresentato il cilindro con
il suo contenuto di gas nelle condizioni di
inizio ciclo.
Ciclo di Carnot - Analisi
Prima trasformazione: La prima trasformazione è una espansione
isoterma, cioè la temperatura del gas si mantiene costante. Per
eseguire tale trasformazione si pone a contatto con una sorgente di
calore, S1 , il cilindro contenente il gas.
Il gas subisce una espansione isoterma (il
pistone si alza) raggiungendo lo stato B.
Al termine della trasformazione le
condizioni del gas sono:
PB = pressione
VB = volume
TB = TA = Ta = temperatura della sorgente
calda.
Ciclo di Carnot - Analisi
Prima trasformazione: Espansione isoterma. Nel piano di
Clapeyron, la isoterma ha la seguente forma.
Ciclo di Carnot - Analisi
Prima trasformazione: Espansione isoterma.
In questa trasformazione il gas assorbe una quantità di calore Qa =
QAB. Poiché la temperatura si deve mantenere costante, tutta
l’energia assorbita viene ceduta all’esterno del sistema sotto forma
di lavoro meccanico, LAB (entrambe le quantità sono positive).Nella
figura il lavoro si trova calcolando l’area, in colore, che si trova
sotto la curva isoterma. A causa dello stretto collegamento tra
energia interna, U, e la temperatura del gas, si ha che l’energia
interna non varia, ed il primo principio della termodinamica assume
la seguente forma:
U  Q

AB



 L AB  Q a  L AB  0
Q

AB

 L AB
Ciclo di Carnot - Analisi
Prima trasformazione: Espansione isoterma.
Il lavoro compiuto dal gas sull’ambiente circostante è positivo e
vale:
Q

AB

L
AB
VB
PA
 n  R  Ta  ln
 n  R  TA  ln
VA
PB
Dove:
n = numero di moli;
R = costante dei gas perfetti.
Ciclo di Carnot - Analisi
Seconda trasformazione: La seconda trasformazione è una
espansione adiabatica, cioè il gas non scambia calore con
l’ambiente circostante. Per fare questo si isola il cilindro
allontanandolo da qualsiasi sorgente di calore.
Il calore scambiato, QBC, è nullo. Nella
trasformazione il gas si espande, il lavoro, LBC,
viene fatto dal sistema sull’ambiente circostante
ed il suo valore è positivo, ne consegue che la
temperatura del gas subisce una diminuzione,
portandosi al valore di Tb = TC. Il gas si porta
nello stato C assumendo i seguenti valori:
PC = pressione
VC = volume
TC = Tb = temperatura della sorgente fredda
Ciclo di Carnot - Analisi
Seconda trasformazione: Espansione adiabatica. Nel piano di
Clapeyron, la adiabatica ha la seguente forma.
Ciclo di Carnot - Analisi
Seconda trasformazione: Espansione adiabatica.
Applicando il primo principio della termodinamica
trasformazione adiabatica si ha:
UBC  QBC LBC
Poiché in una adiabatica il calore, QBC, scambiato è nullo:
QBC  0
allora
U BC  L BC  0
alla
Ciclo di Carnot - Analisi
Seconda trasformazione: Espansione adiabatica.
Il lavoro fatto dal gas sull’ambiente circostante è positivo (poiché è
una espansione) e vale:
LBC  n  c V  R  TB  TC   n  c V  Ta  Tb 
La variazione di energia interna subita dal gas è:
U BC  L BC  n  c V  R  TB  TC 
UBC  n  c V  Ta  Tb   0
Ciclo di Carnot - Analisi
Terza
trasformazione:
La
terza
trasformazione
è
una
compressione
isoterma. Il cilindro, contenente il gas, viene
posto a contatto con una sorgente di calore,
S2, che si trova ad una temperatura più bassa
della sorgente precedente. Il pistone viene
abbassato, la trasformazione è, pertanto, una
compressione isoterma.
Ciclo di Carnot - Analisi
Terza
trasformazione:
L’ambiente
circostante fa un lavoro sul sistema,
l’energia interna non cambia ed il gas cede
calore, QCD, alla sorgente S2. Infatti il gas
riceve dall’esterno dell’energia mediante il
lavoro meccanico e tende ad aumentare la
sua energia interna; poiché l’energia
interna non deve variare (trasformazione
isoterma), allora il gas cede all’esterno
l’energia ricevuta sotto forma di calore.
Ciclo di Carnot - Analisi
Terza trasformazione: Compressione isoterma. Nel piano di
Clapeyron, la isoterma ha la seguente forma.
Ciclo di Carnot - Analisi
Terza trasformazione:
Nella trasformazione il gas passa dallo stato C allo stato A. I
parametri, che descrivono lo stato termodinamico del gas, sono i
seguenti:
PD = pressione
VD = volume
TD = TC = Tb = temperatura della sorgente
fredda
Ciclo di Carnot - Analisi
Terza trasformazione: Anali della trasformazione.
Per il primo principio della termodinamica si hanno le seguenti
situazioni:
U CD  Q

CD

L
Poiché la trasformazione è isoterma, allora
Pertanto si ha
Q  CD  L CD  0
Q  CD  L CD
CD
U CD  0
Ciclo di Carnot - Analisi
Terza trasformazione: Anali della trasformazione.
Il calore ceduto ed il lavoro fatto dall’ambiente circostante sul
sistema sono entrambi negativi.
Il lavoro vale:
Q
Q


CD
VD
 L CD  n  R  TD  ln
VC
CD
PC
 L CD  n  R  Tb  ln
PD


Ciclo di Carnot - Analisi
Quarta trasformazione: La quarta trasformazione è una
compressione adiabatica, quindi il cilindro, contenente il gas,
viene isolato dall’ambiente circostante ed il pistone viene
compresso.
Il calore scambiato, Q , è nullo. Nella
DA
trasformazione il gas si comprime, il lavoro, LDA,
viene fatto sul sistema dall’ambiente circostante
ed il suo valore è negativo; ne consegue che la
temperatura del gas subisce un aumento,
portandosi al valore di Ta = TA. Il gas si porta
nello stato A assumendo i seguenti valori:
PA = pressione
VA = volume
TA = Ta = temperatura della sorgente calda
Ciclo di Carnot - Analisi
Quarta trasformazione : Compressione adiabatica. Nel piano di
Clapeyron, la adiabatica ha la seguente forma.
Ciclo di Carnot - Analisi
Quarta trasformazione: Compressione
adiabatica. Applicando il primo principio
della termodinamica alla trasformazione
adiabatica si ha:
Poiché per una adiabatica:
si ha:
U DA  Q DA  L DA
QDA  0

U DA  L DA
Il lavoro fatto sul sistema 
L DA  n  c v  TD  TA   n  c v  Tb  Ta 
è negativo e vale:
Quindi la variazione
di energia interna è:
U  LDA  n  c v  Tb  Ta   n  c v  Ta  Tb   0
Ciclo di Carnot - Grafico
Il grafico completo del ciclo di Carnot è il seguente:
La misura dell’area racchiusa dalle quattro trasformazioni è il
lavoro fatto dal gas nell’intero ciclo.
Ciclo di Carnot – Analisi dei dati
Adesso sarà analizzato il ciclo dal punto di vista energetico.
Il gas, all’inizio, si trova nello stato A, subisce quattro
trasformazioni termodinamiche e ritorna nello stato A. Come
conseguenza si ha che l’energia interna, U, non cambia, poiché
essa è una funzione di stato. Una funzione di stato è una
grandezza la cui variazione non dipende da come avviene tale
variazione, ma solamente dallo stato iniziale e finale. Poiché gli
stati iniziale e finale coincidono (stato A), la variazione è nulla.
U AA  0
Ciclo di Carnot – Analisi dei dati
Il verso di esecuzione del ciclo termico è orario, pertanto il lavoro
totale che il sistema fa sull’ambiente circostante è positivo.
Il lavoro totale che viene compiuto nel ciclo è:

L Totale  L
AB

L
BC

L

CD
L
DA
Sostituendo i valori trovati in precedenza si ottiene:
L Tot
VB
 n  R  Ta  ln
 n  c V  Ta  Tb  
VA
VD
 n  R  Tb  ln
 n  c v  Tb  Ta 
VC
Ciclo di Carnot – Analisi dei dati
Sostituendo i valori trovati in precedenza si ottiene:
L Tot
VB
 n  R  Ta  ln
 n  c V  Ta  Tb  
VA
VD
 n  R  Tb  ln
 n  c v  Tb  Ta 
VC
Al secondo membro della uguaglianza, il secondo ed il quarto
termine sono uguali e opposti, pertanto la loro somma è nulla. Quindi
il lavoro totale è:
L Tot
VB
VD
 n  R  Ta  ln
 n  R  Tb  ln
 Q  AB  Q  CD
VA
VC
Ciclo di Carnot – Analisi dei dati
In sintesi, tenendo presente che le due quantità di calore scambiate
sono di segno opposto, il lavoro totale fatto nel ciclo è:
L Tot  Q  AB  Q  CD  Q  AB  Q  CD  Q  a  Q  c
Elaborando le espressioni presenti nell’analisi delle quattro
trasformazioni, si ottiene per il lavoro totale una espressione in cui
compaiono le temperature delle due sorgenti di calore utilizzate nel
ciclo.
L Tot
 Ta  Tb  
  Q a
 
 Ta 
Ciclo di Carnot – Rendimento
Il rendimento del ciclo termico è il rapporto fra il lavoro, LTot, che
un sistema fa sull’ambiente circostante ed il calore totale assorbito,
Qa, dal sistema. Applicando la definizione al ciclo di Carnot, si ha:

Q a Q

Qa

c

Q  a - Q- c
Q

a
=1-
Q- c
Q a
Ta - Tb
Tb
=
=1<1
Tb
Ta
Il rendimento è sempre minore di uno. Il rendimento del ciclo di
Carnot aumenta all’aumentare della differenza fra le temperature Ta e
Tb.
Teorema di Carnot
Dagli scritti di Sadi Carnot (S.Carnot: La potenza
motrice del fuoco), E. Clapeyron ha dimostrato che il
rendimento, , del ciclo di Carnot era il massimo
ottenibile da una macchina termica (teorema di
Carnot). Cioé, il rendimento termico di un arbitrario
ciclo reversibile, funzionante con i medesimi
termostati (i due termostati sono la sorgente a
temperatura più alta, Ta, e la sorgente a temperatura più
bassa, Tb), non può essere superiore al rendimento del
ciclo di Carnot reversibile.
Teorema di Carnot
Un’importante conseguenza del teorema di Carnot è che
tutte le macchine di Carnot che lavorano fra gli stessi
due termostati hanno lo stesso rendimento. Questo
risultato indica che il rendimento della macchina di
Carnot è un parametro universale, indipendente cioè
dalla natura specifica del sistema che costituisce la
macchina (cioè è indipendente dalla natura del fluido
di lavoro). Il rendimento dipende, cioè, solo dalle
temperature dei due termostati.
Teorema di Carnot
Indicando con R il rendimento di una macchina di
Carnot che funzioni mediante trasformazioni reversibili e
con I il rendimento della stessa macchina che funzioni
mediante trasformazioni irreversibili e con gli stessi
termostati, si verifica sempre che il rendimento della
macchina con trasformazioni irreversibili è sempre
più piccolo di quello della macchina con
trasformazioni reversibili.
I < R
Teorema di Carnot
Dal libro di Sadi Carnot (La potenza motrice del fuoco),
E. Clapeyron ha mostrato che per il ciclo termico di
Carnot vale il seguente importante teorema: Tra tutte le
macchine termiche operanti tra le stesse temperature
estreme (Ta e Tb ), la macchina di Carnot è quella dotata
del massimo rendimento. Inoltre il rendimento del ciclo
di Carnot non dipende dalla natura dell’agente termico
presente nella macchina, ma è unicamente funzione dei
due valori della temperatura.
Teorema di Carnot
Quindi il rendimento del ciclo di Carnot è il massimo che si può
ottenere da una macchina termica. Inoltre tutte le macchine di
Carnot che lavorano fra gli stessi due termostati hanno lo stesso
rendimento. In sintesi, se il rendimento di una qualsiasi macchina
termica reversibile è Rev, questo valore non può mai essere
superiore al rendimento, Rev(Carnot), di un ciclo reversibile di
Carnot realizzato fra le stesse temperature Ta e Tb
Rev  rev(Carnot)
Pertanto si ha:
Rev
Tb
 Rev Carnot   1 
Ta
Teorema di Carnot
Il rendimento, Irrev(Carnot), di un ciclo irreversibile di Carnot è
sempre più piccolo di quello, Rev(Carnot), di un ciclo di
reversibile di Carnot realizzati fra le stesse temperature estreme Ta
e Tb [Irrev(Carnot) < Rev(Carnot)]. Il rendimento di un ciclo
irreversibile di Carnot:
Irrev  1 
Q- c
Q a
Tb
 Rev  1 
Ta
Disuguaglianza di Clausius
Per un generico ciclo termodinamico vale una importante
disuguaglianza di Clausius. Tenendo presente il rendimento sia
del ciclo reversibile che del ciclo irreversibile di Carnot si ricava:

Q- c
Q

a
Tb

Ta
 
Q- c
Tb

Q a
Ta

Qa
Ta

Q- c
Tb
0
Il segno di uguale (=) vale per il ciclo reversibile di Carnot; il
segno di disuguaglianza (<) vale per il ciclo irreversibile di
Carnot.
Disuguaglianza di Clausius
Prendendo i valori algebrici e non quelli assoluti del calore, si ha:
Qa Qc

0
Ta
Tb
Il segno di uguale (=) vale per il ciclo reversibile di Carnot; il
segno di disuguaglianza (<) vale per il ciclo irreversibile di
Carnot.
Disuguaglianza di Clausius
La precedente relazione la si può generalizzare al caso in cui si ha
un un ciclo termico che utilizza diverse sorgenti di calore (Q1, Q2,
Q3, Q4,..... Qn) che si trovano a diverse temperature (T1, T2, T3,
T4, .......Tn). La relazione in forma sintetica si scrive:
n
Q1 Q2 Q3 Q4
Qn
Qi



 ......... 
0 
0
T1 T2 T3 T4
Tn
i1 Ti
Questa importante relazione è detta disuguaglianza di Clausius e
serve per giudicare la fattibilità di un ciclo termico che viene
proposto.
Disuguaglianza di Clausius
Nelle più generali trasformazioni termodinamiche, la temperatura
cambia con continuità ed il sistema scambia quantità elementari di
calore, Q, con l’ambiente circostante.
Pertanto in un ciclo termico qualsiasi la relazione di Clausius
diventa:
n

i 1
Q i
0
Ti
 Il segno di uguaglianza (=) vale per un ciclo reversibile



 Il segno di disuguaglianza (<) vale per un ciclo irreversibile 
Disuguaglianza di Clausius
Le quantità Qi,ovvero Qi, sono positive se il calore è
assorbito dal sistema, mentre sono negative se vengono
cedute dal sistema all’ambiente circostante.
Quando si progetta un ciclo termico è necessario che
contemporaneamente soddisfi alle due seguenti
condizioni:
1)il rendimento non deve essere superiore al ciclo di
Carnot, che ha due sorgenti di calore le cui temperature
siano la massima e la minima del ciclo che si sta
progettando;
2)deve essere soddisfatta la relazione di Clausius.
Fine