2
A4
Regolatori
switching
I regolatori di tensione lineari hanno il grave difetto di non consentire il raggiungimento di valori di efficienza particolarmente elevati. Infatti, in queste architetture gli elementi di regolazione
dissipano un quantitativo di potenza tutt’altro che trascurabile. Chiunque abbia utilizzato un regolatore lineare integrato come il 7805, sa che questi componenti possono facilmente raggiungere temperature molto elevate, e necessitano sempre l’utilizzo di un dissipatore. La ricerca continua, in ambito industriale, di regolatori sempre più efficienti ha condotto alla realizzazione dei
cosiddetti regolatori switching o SMPS (Switching Mode Power Supply). Un regolatore di tipo
switching può raggiungere valori di efficienza superiori al 95%, bel al di sopra di quanto si possa
ottenere con le migliori realizzazioni di natura lineare.
In questa unità verranno prese in esame le fondamentali architetture di regolatori switching:
step down e step up. Sebbene esistano molte altre architetture più sofisticate, queste due sono
alla base di qualsiasi ulteriore sviluppo.
A4.1 Generalità
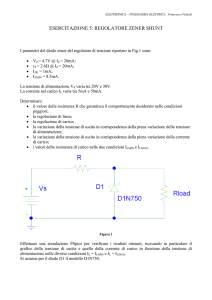
Come si è visto nella prima unità di questo modulo, un regolatore di tensione è un circuito il cui scopo è quello di trasformare un livello di tensione continua in ingresso Vin,
soggetto a fluttuazioni imprevedibili e indesiderate, in una tensione di uscita Vout esente
da tali fluttuazioni e in genere di valore diverso. Lo schema concettuale generale di un
regolatore lineare è riportato nella figura A4.1.
Figura A4.1
Schema generale
di un regolatore
lineare di tensione.
RS
Vin
Iout
IS
RL
Vout
In questo schema è possibile regolare la tensione di uscita agendo sulla resistenza
RS oppure sulla corrente IS. In generale si possono adottare due strategie per il controllo.
•
Controllo di tipo parallelo. Si agisce sul valore della corrente IS mantenendo costante il valore di RS. In questo modo la potenza dissipata dal convertitore assume
la seguente espressione:
PDC–DC = Vout · IS + RS · (Iout + IS)2
3
A1 • Regolatori switching
Si può notare come la potenza dissipata dal convertitore (escluso quindi il carico
RL) non si annulla neanche nel caso estremo in cui si ponga IS = 0.
•
Controllo di tipo serie. Se invece si elimina il generatore di corrente (IS = 0) e si
agisce sul resistore RS, l’espressione della potenza dissipata assume la seguente
forma:
RS
PDC – DC = Vin2
( RS + RL )
Questa espressione si annulla nei casi RS = 0 e RS = ∞. Si tratta ovviamente di casi
limite, poiché in entrambe le situazioni la regolazione della tensione di uscita di
fatto cessa.
Questa particolarità del controllo di tipo serie è alla base dello sviluppo dei regolatori di tipo switching.
A4.2 Il convertitore Buck
In un regolatore switching l’elemento resistivo viene sostituito da un dispositivo di
commutazione a semiconduttore, per esempio un MOSFET. Questo dispositivo possiede un valore resistivo molto basso se viene fatto condurre in zona ohmica, e molto
alto quando è interdetto. Il MOSFET viene quindi fatto lavorare in commutazione, a
una frequenza che può assumere valori dell’ordine della decina di kHz: in questo modo
la dissipazione di potenza nel dispositivo rimane estremamente limitata. La tensione
continua di ingresso vin viene convertita dal transistor in un’onda rettangolare, di frequenza pari alla frequenza di commutazione del transistor stesso. A valle del MOSFET,
prima del carico RL, viene quindi posto un filtro passa basso di tipo non dissipativo, per
esempio un filtro passivo LC, per estrarre il valore medio dell’onda rettangolare e produrre in uscita una tensione vout continua del valore desiderato.
Quanto detto è mostrato schematicamente nella figura A4.2. Questo tipo di regolatore prende il nome di regolatore di tipo buck o step down, in quanto la tensione di
uscita è necessariamente più bassa di quella di ingresso. Il pregio principale di questo
tipo di architettura è il valore particolarmente elevato di efficienza rispetto alle architetture di tipo lineare: infatti sia il transistor che il filtro passivo dissipano un quantitativo di potenza estremamente limitato.
Figura A4.2
Schema di un
regolatore
switching di tipo
buck o step down.
Elemento serie
DQ
Q
vin
Filtro
passa basso
Cin
A
LLP
DR
CLP
RL
vout
4
Modulo A • Alimentatori stabilizzati
L’analisi del funzionamento del circuito può essere svolta separando la fase in cui
il transistor è in conduzione (interruttore chiuso) da quella in cui il transistor è interdetto (interruttore aperto). A questo scopo si faccia riferimento allo schema riportato
nella figura A4.3. Si noti come l’analisi così svolta è di tipo statico, cioè ipotizza che
in ciascuna fase si siano esauriti i transitori di commutazione. Ipotizzeremo inoltre che
––
la tensione di ingresso sia costante: vin = Vin.
Figura A4.3
Schema
semplificato
di un regolatore
step down.
A
Q
vin
•
Figura A4.4
Regolatore
step down.
Transistor Q
in conduzione.
LLP
CLP
DR
RL
vout
Interruttore chiuso (transistor in conduzione). Quando il transistor Q è in con––
duzione il diodo DR è polarizzato inversamente (–vD = Vin – VQ(on)) e non conduce.
Il circuito può essere rappresentato come nella figura A4.4.
A
Q
vin
LLP
CLP
DR
RL
vout
Dal momento che si può facilmente ottenere VQ(on) ≅ 0 il potenziale del nodo A, vA,
assume il seguente valore:
––
vA = –vD ≅ Vin
[A4.1]
A transitorio esaurito la tensione ai capi dell’induttore LLP vale:
––
vL = Vin – VQ(on) – vout
•
[A4.2]
Interruttore aperto (transistor interdetto). Quando il transistor Q è interdetto il
diodo DR è polarizzato direttamente e conduce (vD = Vγ ). Il circuito può essere rappresentato come nella figura A4.5.
Figura A4.5
Regolatore step
down. Transistor Q
interdetto.
A
Q
vin
LLP
DR
CLP
RL
vout
Il diodo entra in conduzione perché, al momento della commutazione del transistor,
l’induttore LLP non può modificare il proprio flusso di corrente istantaneamente, ma
deve scaricarsi gradualmente. Perché questo accada, il potenziale del nodo A cambia
bruscamente segno e diventa negativo, anche se di poco (Vγ ≅ 0) affinché la corrente
5
A1 • Regolatori switching
possa continuare a scorrere nell’induttore nello stesso verso:
[A4.3]
vA = –vD = –Vγ ≅ 0
Dal momento che, non variando la corrente, non varia nemmeno la tensione di
uscita, questo cambio di segno si riflette nella tensione ai capi dell’induttore stesso, che
si inverte:
vL = –vout – Vγ
[A4.4]
•
Tensione e corrente di uscita. Il potenziale del nodo A del regolatore step down,
vA, assume quindi l’andamento di un’onda rettangolare con frequenza e duty cycle
pari a fequenza e duty cycle del segnale CMD che comanda la commutazione del
transistor Q. Se la frequenza di questo segnale, fCMD =
maggiore della frequenza di taglio del filtro LC, f LP =
Toff
1
1
= , è molto mag+ Ton T
1
, cioè se risulta
2π LLP C LP
fCMD >> fLP allora la tensione di uscita del regolatore step down sarà pari al valore
medio della tensione vA, in quanto tutte le componenti armoniche di vA verranno
soppresse dal filtro stesso. Si ottiene quindi:
––
vout ≅ ––
vA ≅ δ Vin
dove si ha δ =
[A4.5]
TON
T
= ON .
TON + TOFF
T
Se la tensione di uscita è sostanzialmente costante, altrettanto costante risulta essere
la corrente che attraversa il carico RL:
iRL =
vout vA δ Vin
≅
≅
RL
RL
RL
[A4.6]
Quanto appena illustrato è rappresentato nella figura A4.6.
Vin
vA
vout
Figura A4.6
Potenziale del
nodo A (traccia
nera) e tensione di
uscita (traccia blu)
del convertitore
step down.
δVin
T
TON
TOFF
t
Le correnti dell’interruttore
• Interruttore chiuso (transistor in conduzione). Quando l’interruttore è chiuso, la
tensione ai capi dell’induttore vale, a transitorio esaurito (si veda la [A4.2]):
––
––
––
vL = Vin – VQ(on) – δ Vin ≅ (1 – δ) Vin
valore che, essendo costante, determina nell’induttore una corrente lineare che ha la
seguente espressione:
iL ( t ) = iL ( 0 ) +
(1 − δ )Vin
LLP
t
6
Modulo A • Alimentatori stabilizzati
Al termine del periodo di conduzione la corrente assume il seguente valore:
iL (TON ) = iL ( 0 ) +
•
(1 − δ )Vin
LLP
TON = i1
[A4.7]
Interruttore aperto (transistor interdetto). Quando il transistor Q è interdetto, la
tensione ai capi dell’induttore vale, a transitorio esaurito (si veda la [A4.4]):
––
––
vL = –δ Vin – Vγ ≅ –δ Vin
La corrente nell’induttore inizia quindi a diminuire linearmente, e assume la seguente espressione:
iL ( t ) = i1 ( 0 ) −
δ Vin
t
LLP
raggiungendo, dopo Toff secondi dalla commutazione, il valore:
(
)
iL Ton + Toff = iL (T ) = i1 −
Figura A4.7
Correnti nell’induttore (traccia nera), nel
carico (traccia blu) e
nel condensatore
(traccia grigia) del regolatore step down.
δ Vin
Ton + Toff = i2
LLP
(
)
[A4.8]
i L i RL i C
i1
(i1+i2)/2
i2
t
T
TON
TOFF
L’escursione di corrente nell’induttore vale perciò:
Δ iL = i1 − i2 = δ
Vin
T
LLP
[A4.9]
Si può dimostrare che la corrente che scorre nel carico RL è pari al valore medio tra
i1 e i2:
i +i
[A4.10]
iRL ≅ 1 2
2
la variazione di corrente nell’induttore, Δi , verrà quindi interamente assorbita dal
condensatore. Questa situazione è mostrata nella figura A4.7.
L
7
A1 • Regolatori switching
Forme d’onda del convertitore buck
Quanto finora illustrato viene riassunto graficamente nella figura A4.8. Ricordando
l’analisi svolta si può notare come il transistor Q conduce durante la fase di carica dell’induttore, mentre la scarica avviene attraverso il diodo di ricircolo DR. Il diodo e il
transistor infatti entrano in conduzione in modo alternativo.
vCMD
vQ
t
t
i1
i2
iQ
t
vA1
vA vA2
t
vD
t
i1
i2
iD
t
(1-δ)Vin
vL
t
-δVin
i1
iL
i2
t
Ton
Toff
T
Il potenziale vA assume quindi la forma di un’onda rettangolare di ampiezza so––
stanzialmente pari a Vin. Il valore medio di quest’onda rettangolare viene quindi ottenuto in uscita attraverso il filtro passa basso.
A4.3 Criteri di progetto di un convertitore buck
Anziché proporre un elenco di formule per il dimensionamento di un convertitore step
down, si preferisce condurre l’analisi di un caso reale utilizzando Multisim. Lo schema
proposto può essere facilmente riadattato a molte situazioni pratiche modificando la
frequenza di taglio del filtro e la scelta di MOSFET e diodo, quando non siano presenti
specifiche troppo stringenti o che riguardino troppi parametri del circuito.
Si consideri il circuito mostrato nella figura A4.9. Essa riporta lo schema, realizzato con Multisim, di un regolatore step down: si tratta di una rielaborazione (e semplificazione) del circuito di esempio di regolatore step down Buck_VM.ms11 reperibile nella cartella samples, seguendo il percorso SMPS Circuits\Transient Analysis.
•
Il regolatore utilizza il MOSFET di potenza a canale N IRFP044N, caratterizzato
da tensione di soglia Vth compresa tra Vth(min) = 2 V e Vth(max) = 4 V, tensione mas-
Figura A4.8
Forme d’onda del
regolatore step
down.
8
Modulo A • Alimentatori stabilizzati
sima tra gate e source VGS(max) = 20 V, potenza massima dissipata PD(max) = 120 W,
massima corrente di drain ID(max) = 37 A e massima resistenza drain-source in conduzione RDS,ON(max) = 20 mΩ (i dati sono forniti da International Rectifier).
•
Il diodo di ricircolo è un diodo Schottky di potenza caratterizzato da una tensione
di soglia Vγ piuttosto bassa (Vγ(typ) = 0,35 V con corrente diretta IF = 1 A e temperatura della giunzione Tj = 25 ° C, dati forniti da ON Semiconductor).
LQ
Figura A4.9
Regolatore step
down realizzato
con Multisim.
4
,5)31
&0'
$
/B/3
RXW
+
9BLQ
9B&0'
9
N+]
9
'B5
0%567
&B/3
)
5B/
ȍ
Le caratteristiche del MOSFET e del diodo fanno sì che si possa avere con ottima
––
approssimazione vA(ON) ≅ Vin = 3,2 V e vA(OFF) ≅ 0 V.
•
La frequenza di taglio del filtro passivo vale:
f LP =
1
1
=
≅ 758 Hz
2π LLP C LP 2π 200 ⋅ 10 −6 ⋅ 220 ⋅ 10 −6
per cui risulta, come è necessario che sia, fCMD = 50 kHz >> fLP.
•
Per condurre la simulazione si è posto inizialmente δ = 0,75. Inoltre si è scelto un
valore della tensione di comando molto maggiore della tensione di soglia, per spingere il più possibile il MOSFET in zona ohmica.
La simulazione (Transient Analisys) è stata svolta in un intervallo di tempo di 10
ms. I risultati sono riportati nei seguenti grafici.
•
Andamento della tensione di uscita. La figura A4.10 mostra l’andamento nel
––
tempo della tensione di uscita del regolatore. Dal momento che si ha Vin = 3,2 V ci
––
si aspetta per la tensione di uscita il valore di regime vout(t → ∞) = δ Vin = 0,75 · 3,2
= 2,4 V. La simulazione restituisce il valore vout(0,01) = 2,32 V, in ottimo accordo
con la previsione.
Si può inoltre notare il tipico andamento della risposta di un sistema del secondo ordine con poli complessi coniugati a parte reale negativa, quale è in effetti il filtro
LC completo di carico RL. Si possono facilmente ricavare la pulsazione naturale
della coppia di poli, lo smorzamento ζ e quindi la massima sovraelongazione per-
9
A1 • Regolatori switching
centuale sul valore di regime, M%, e il tempo di assestamento al 95% del sistema,
TA,0.05:
ωn =
ς=
1
=
LLP C LP
1
200 ⋅ 10 −6
⋅ 220 ⋅ 10 −6
≅ 4800
rad
s
LLP 1 200 ⋅ 10 −6
=
= 0,12
C LP 8 200 ⋅ 10 −6
1
2 RL
M % = 100 e
−
πξ
1−ξ 2
= 100 e
−
0,12π
1− 0,12 2
= 68, 4%
Dal momento che si ha vout (0,01) = 2,32 V ci si aspetta vout(max) = (1 + 0,684) ·
vout(0,01) = 1,684 · 2,32 ≅ 3,9 V. Dall’analisi del grafico si ricava vout(max) = 3,83 V.
Per il tempo di assestamento si ottiene infine:
TA,0,05 ≅ −
1
1
ln ( 0, 05 ) ≅
ln ( 0, 05 ) ≅ 5, 2 ms
4800 ⋅ 0,12
ω nξ
Si verifica facilmente dall’esame del grafico come in effetti l’assestamento si verifichi in circa 5 ms.
Figura A4.10
Andamento della
tensione di uscita
del regolatore step
down.
7HQVLRQHGLXVFLWD9
P
P
P
P
7HPSRV
•
Tensione di uscita a regime e tensione vA. La figura A4.11 mostra la relazione tra
la forma d’onda della tensione vA e il valore della tensione di uscita vout a regime. Si
nota facilmente come il valore della tensione di uscita corrisponda effettivamente al
valore medio della tensione vA.
•
Correnti nell’induttore, nel condensatore, nel carico. La mostra infine le correnti a regime nell’induttore LLP, nel condensatore CLP, nel carico RL. Si ricavano
innanzitutto dal grafico i valori delle correnti i1 e i2:
i1 = 610 mA
i2 = 546 mA
Si vede poi come la corrente nel carico risulti sostanzialmente costante e pari a:
iRL =
i1 + i2 0, 61 + 0, 546
=
= 578 mA
2
2
10
Modulo A • Alimentatori stabilizzati
Infine si vede come la corrente che attraversa il condensatore vari tra i valori iC,1 =
32 mA e iC,2 = –32 mA.
Figura A4.11
Relazione tra tensione di uscita
(traccia blu)
e tensione vA
(traccia nera).
7HQVLRQH9
P
P
P
P
P
7HPSRV
Soppressione delle oscillazioni della tensione di ingresso
Per concludere l’analisi del funzionamento di un regolatore switching di tipo step
down, si opera una modifica del circuito della figura A4.9, inserendo in serie al gene––
ratore Vin un generatore sinusoidale di ampiezza VN = 0,1 V e frequenza FN = 5000 Hz.
Il nuovo circuito è riportato nella figura A4.13. Il generatore sinusoidale simula di
fatto la presenza di oscillazioni indesiderate nella tensione di ingresso vin: si ottiene in––
fatti per il nuovo circuito vin = Vin + VN sin(2π fN t) = 3,2 + 0,1 sin(2π · 5000 · t).
Figura A4.12
Correnti nell’induttore (traccia nera),
nel carico (traccia blu)
e nel condensatore
(traccia grigia)
del regolatore step
down.
P
P
P
&RUUHQWH$
P
P
P
P
P
P
P
P
P
P
P
7HPSRV
I risultati della simulazione, riportati nella figura A4.14, sono estremamente interessanti. Si vede infatti come l’oscillazione in ingresso venga sostanzialmente soppressa dal circuito. Questo avviene perché l’oscillazione introdotta ha una frequenza
fN = 5000 Hz significativamente maggiore della frequenza di taglio del filtro passa
basso (fLP = 758 Hz)). Dal momento che l’oscillazione non modifica il valore medio
11
A1 • Regolatori switching
della tensione di ingresso, il valore della tensione di uscita a regime non cambia.
Naturalmente oscillazioni a frequenza minore di fLP non verrebbero soppresse, e si ripresenterebbero sostanzialmente inalterate nella forma d’onda d’uscita. In ogni caso il
regolatore step down si dimostra capace di assorbire oscillazioni indesiderate nella tensione di ingresso, almeno a frequenze sufficientemente alte.
Figura A4.13
Regolatore step
down con generatore sinusoidale in
ingresso.
LQ
9B1
4
9UPV
+]
,5)31
&0'
/B/3
$
RXW
+
9BLQ
9B&0'
9
N+]
9
'B5
5B/
&B/3
0%567
ȍ
)
Figura A4.14
Tensione di
ingresso (traccia
nera) e tensione di
uscita (traccia blu)
del regolatore della
figura A4.13.
7HQVLRQH9
P
P
P
P
7HPSRV
A4.4 Il convertitore Boost
Un regolatore step up (o regolatore boost) è in grado di produrre una tensione di uscita
vout di valore superiore alla tensione di ingresso vout. Lo schema di un regolatore step
up è riportato nella figura A4.15.
A
L
vin
Cin Q
Figura A4.15
Schema di un
regolatore step up
o boost.
DR
DQ
C
RL
vout
12
Modulo A • Alimentatori stabilizzati
Come nel caso dei regolatori step down, l’analisi del funzionamento del circuito
può essere svolta separando la fase in cui il transistor è in conduzione (interruttore
chiuso) da quella in cui il transistor è interdetto (interruttore aperto).
Figura A4.16
Schema semplificato
di un regolatore
step up.
A
L
DR
vin
Q
RL
C
vout
Si faccia riferimento a tal proposito alla figura A4.16. Si noti come l’analisi così
svolta è anche in questo caso di tipo statico, cioè ipotizza che in ciascuna fase si siano
esauriti i transitori di commutazione. Ipotizzeremo inoltre, come per il regolatore step
––
down, che la tensione di ingresso sia costante: vin = Vin.
•
Interruttore chiuso (transistor in conduzione). Quando il transistor MOSFET
conduce (in zona ohmica), il diodo non conduce. Questa situazione è rappresentata
nella figura A4.17. Si ha infatti:
vA = VQ(on) ≅ 0 V
[A4.11]
e quindi vD = –vout. La tensione ai capi dell’induttore coincide quindi con la tensione di ingresso:
––
vL = vin = Vin
[A4.12]
Essendo vL costante, la corrente nell’induttore aumenta linearmente secondo la seguente espressione:
iL ( t ) = iL ( 0 ) +
Vin
t
L
e al termine del periodo di conduzione assume il seguente valore:
iL (TON ) = iL ( 0 ) +
Figura A4.17
Regolatore step up.
Transistor Q
in conduzione.
Vin
TON = i1
L
[A4.13]
A
L
vin
DR
Q
C
RL
vout
Dall’altro lato del circuito, il condensatore C si scarica sul resistore RL, determinando ovviamente la presenza di un ripple residuo nella forma d’onda della tensione di
uscita. È necessario che il valore della capacità C risulti sufficientemente alto, affinché
la corrente che il condensatore cede al carico durante il periodo TON determini una diminuzione minima della tensione ai capi del condensatore stesso.
•
Interruttore aperto (transistor interdetto). Quando il transistor Q è interdetto il
diodo D è polarizzato direttamente e conduce. Questa situazione è rappresentata
nella figura A4.18.
13
A1 • Regolatori switching
A
L
vin
Figura A4.18
Regolatore step up.
Transistor Q interdetto.
DR
Q
RL
C
vout
Il diodo entra in conduzione perché, al momento della commutazione del transistor,
l’induttore L non può modificare il proprio flusso di corrente istantaneamente, ma
deve scaricarsi gradualmente. Perché questo accada, la tensione ai capi dell’induttore cambia bruscamente segno e diventa negativa, affinché la corrente possa continuare a scorrere nell’induttore nello stesso verso. Si ha quindi:
vA = vout + Vγ ≅ vout
[A4.14]
––
vL = vin –(vout + Vγ ) ≅ Vin – vout
[A4.15]
e di conseguenza:
Si noti come debba essere necessariamente vL < 0, e quindi risulti:
––
Vin < vout
[A4.16]
A causa dell’elevato valore del condensatore C, la tensione di uscita rimane costante anche durante il periodo di interdizione del transistor. La corrente nell’induttore
allora decresce linearmente secondo la relazione:
iL ( t ) = i1 +
Vin − vout
t
L
e al termine del periodo di interdizione assume il seguente valore:
iL (TON + TOFF ) = i1 −
•
Vin − vout
L
(TON + TOFF ) = i2
[A4.17]
Tensioni di ingresso e di uscita. Quanto appena descritto permette di ricavare la
relazione ingresso uscita di un regolatore step up. Infatti, se a regime la tensione di
––
uscita vout è costante, ed è costante anche la tensione di ingresso Vin, allora l’escursione della corrente nell’induttore L durante il periodo di conduzione di Q deve
eguagliare con segno opposto quella che si verifica durante il successivo periodo di
interdizione:
ΔiL(TON) = –ΔiL(TOFF)
ovvero, in termini di tensione, ricordando che per un induttore si ha
iL ( t ) =
1 t
vL (τ ) dτ :
L ∫0
vL(on)TON = –vL(off)TOFF
e quindi:
––
––
VinTON = –(Vin – vout)TOFF
[A4.18]
14
Modulo A • Alimentatori stabilizzati
da cui si ricava, con semplici passaggi:
vout =
con δ =
Vin
1− δ
[A4.19]
TON
.
TON + TOFF
La figura A4.19 mostra graficamente la relazione tra il duty cycle δ del segnale di
comando del transistor Q e il rapporto
Figura A4.19
Relazione tra duty
cycle e rapporto
ingresso/uscita del
regolatore.
vout
.
vin
1 000
Vout / Vin
100
10
1
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Naturalmente non è pensabile che un regolatore boost reale possieda una caratteristica ingresso uscita uguale a quella della figura A4.19. In tal caso infatti si potrebbe
aumentare indefinitamente il valore della tensione di uscita semplicemente aumentando il duty cycle del segnale di comando. Nella pratica l’andamento è quello mostrato nella figura A4.20.
Figura A4.20
Caratteristica di un
regolatore step up
reale (traccia nera).
1 000
Vout / Vin
100
10
1
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
15
A1 • Regolatori switching
Forme d’onda del regolatore step up
Quanto finora illustrato viene riassunto graficamente nella figura A4.21. È facile notare le fortissime analogie con i segnali relativi al convertitore step down, così come le
significative differenze illustrate nel paragrafo precedente.
vCMD
vQ
iQ
Figura A4.21
Forme d’onda di un
regolatore step up.
t
t
i1
i2
t
vout
vA
t
vD
t
i1
iD
i2
t
Vin
vL
t
-(δVin)/(1-δ)
i1
iL
i2
t
Ton
Toff
T
A4.5 Il convertitore Buck-Boots
Un regolatore buck-boost combina l’architettura di un regolatore step down e di un regolatore step up. Uno schema di principio è riportato nella figura A4.22.
L
vin
Q1
Q2
Q3
Logica di
controllo
Q4
C
RL
vout
Figura A4.22
Schema di principio
di un convertitore
buck-boost.
16
Modulo A • Alimentatori stabilizzati
Il funzionamento del circuito è molto semplice, una volta che si sia compreso il funzionamento dei regolatori buck e boost separatamente. Infatti, i transistor Q1 e Q2 costituiscono la sezione step down, mentre i transistor Q3 e Q4 realizzano la sezione step
up.
Il funzionamento del regolatore si può schematizzare come segue:
•
Regolatore step down. Il transistor Q4 rimane sempre in conduzione, mentre il
transistor Q3 rimane sempre interdetto. Il transistor Q1 carica l’induttore L durante
la sua fase di conduzione, mentre il transistor Q2 ne permette la scarica, svolgendo
la funzione di un diodo di ricircolo.
•
Regolatore step up. Il transistor Q1 rimane sempre in conduzione, mentre il transistor Q2 rimane sempre interdetto. Il transistor Q3 permette la carica dell’induttore
L durante la sua fase di conduzione, mentre il transistor Q4 ne permette la scarica.
A4.6 Confronto tra regolatori lineari
e regolatori switching
Nella precedente unità si è visto come i regolatori lineari di tipo LDO, caratterizzati da
un valore molto basso di tensione di dropout, siano caratterizzati da valori di efficienza
nettamente superiori rispetto ai semplici regolatori lineari come il 7805. In particolare
si è svolto il calcolo dell’efficienza per il modello TPS76333, ricavando il valore
η = 75,99% a fronte di un valore di η = 14,9% ottenuto con il 7805.
Per valutare le performance di un regolatore switching, si prenda in esame il grafico
riportato nella figura A4.23, che mostra l’efficienza al variare della corrente assorbita
dal carico di un regolatore step down prodotto da Texas Instruments.
96
TA = 25°C
VOUT = 1.8 V
fSW = 500 kHz
94
92
Efficiency (%)
Figura A4.23
Efficienza di un regolatore step down
prodotto da Texas
Instruments.
90
88
86
84
VIN = 5 V
VIN = 12 V
VIN = 17 V
82
80
2
3
4
5
6
7
Load Current (A)
8
9
10
G000
Come si può notare, i valori di efficienza possono superare anche di venti punti percentuali quelli di un regolatore LDO, confermando l’elevatissima efficienza di questa
categoria di dispositivi.
Test di verifica
Quesiti a risposta aperta
1. Illustrare l’idea alla base di un regolatore step down, disegnandone uno schema di massima.
2. Descrivere il principio di funzionamento di un regolatore step down, separando l’analisi nelle due fasi di funzionamento (transistor in zona ohmica, transistor interdetto).
3. Ricavare la relazione ingresso uscita di un regolatore step down.
4. A quale condizione un regolatore step down è in grado di sopprimere oscillazioni indesiderate nella tensione
di ingresso?
5. Disegnare le forme d’onda di un regolatore step down, commentandole opportunamente.
6. Disegnare lo schema di un regolatore step up, commentandolo opportunamente.
7. Descrivere il principio di funzionamento di un regolatore step up, separando l’analisi nelle due fasi di funzionamento (transistor in zona ohmica, transistor interdetto).
8. Ricavare la relazione ingresso uscita di un regolatore step up.
9. Disegnare le forme d’onda di un regolatore step up, commentandole opportunamente.
10. Disegnare lo schema di un regolatore buck-boost, commentandolo opportunamente.
Quesiti a scelta multipla
Scegliere la risposta corretta tra quelle proposte.
1. Un regolatore switching riesce a ottenere un’elevata efficienza grazie a:
a L’utilizzo di soli componenti passivi.
b L’utilizzo di componenti reattivi e transistor in commutazione.
c L’utilizzo di diodi Schottky.
d L’utilizzo di componenti molto piccoli.
2. Per regolare la tensione di uscita di un regolatore step down occorre:
a Variare il valore del carico in uscita.
b Variare il valore della tensione di ingresso.
c Variare il duty cycle del segnale di comando del transistor.
d Variare il valore dell’induttanza del filtro.
3. Affinché un regolatore step down possa attenuare le oscillazioni della tensione di ingresso occorre che
risulti:
a f ≅f
LP
N
b f << f
LP
N
c f >> f
LP
N
d Nessuna delle precedenti.
17
Esercitazioni
A1 • Regolatori switching
Esercitazioni
18
Modulo A • Alimentatori stabilizzati
4. La corrente che attraversa il carico di un regolatore step down è:
a Costante.
b Nulla.
c Uguale a quella che attraversa l’induttore.
d Nessuna della precedenti.
5. Un regolatore step up:
a Permette di regolare a piacere la tensione di uscita.
b Permette di ottenere tensioni di uscita maggiori o minori della tensione di ingresso.
c Permette di ottenere solo tensioni superiori a quelle di ingresso.
d Permette di ottenere solo tensioni minori di quelle di ingresso.
6. Un regolatore step up reale:
a Per valori elevati di duty cycle produce una tensione di uscita nulla.
b Per valori elevari di duty cycle si comporta come un regolatore step down.
c Per valori elevati di duty cycle produce una tensione di uscita uguale a quella di ingresso.
d Nessuna delle precedenti.
7. Un regolatore buck-boost:
a Deve necessariamente utilizzare dei transistor al posto dei diodi.
b Dissipa necessariamente più potenza di un regolatore step up o step down.
c È sempre più efficiente di un regolatore step down.
d Nessuna delle precedenti.