Aritmetica 1_Informatica

g. Ferrari
m. cerini
d. giallongo
Piattaforma
Piattaforma
matematica
Informatica
tREvIsInI EDITORE
Aritmetica 1
Informatica
Excel: la matematica con i fogli di calcolo
Excel è il programma di fogli di calcolo, o fogli elettronici, più diffuso ed è prodotto
da Microsoft. È compreso nel “pacchetto” Office, assieme a Word e ad altri programmi. Noi analizzeremo la versione Office 2010. L’estensione .xlsx, usata dalla
versione 2007 in poi, identifica la maggior parte dei fogli di calcolo creati con Excel.
Per avviare Excel la prima volta si clicca sul pulsante Avvio, si seleziona Tutti
i programmi e, aprendo la cartella Microsoft Office si trova Excel. Per un
avvio più veloce l’icona del programma si può trascinare o nella Barra delle
applicazioni (in basso) o nel Desktop.
L’uso di Excel, nella versione del pacchetto Office 2010, è molto facile e intuitivo perché dalla barra dei menu, per ogni voce (Home, Menu, Inserisci, …) si apre un pannello di controllo dove è semplice e veloce trovare tutte le funzioni del programma.
A differenza di Word, la pagina di Excel è suddivisa, come in un quaderno
a quadretti, in tante (da cui il nome Ex-cel), ognuna indipendente dalle altre.
Caratteristica di Excel è la Barra della formula, che comprende due rettangoli, quello a sinistra detto “casella nome” in cui è indicata la cella su cui si sta
lavorando, e quello a destra, più grande, in cui è indicato il contenuto della
suddetta cella (nell’esempio B3 – foglio elettronico).
Il foglio di lavoro occupa la parte centrale della finestra ed è formato da righe
numerate e da colonne contrassegnate da lettere dell’alfabeto. All’incrocio
di ciascuna riga con ciascuna colonna ci sono le celle che sono individuate,
come nella battaglia navale e nelle coordinate geografiche, con la lettera della
colonna seguita dal numero della riga (A1, B3, C4, ...).
La cella sulla quale si sta lavorando è facilmente individuabile perché circondata
da un riquadro più scuro e indicata nella casella nome della barra della formula.
Il foglio elettronico esiste da pochi decenni e ha semplificato molto il lavoro nel
campo della matematica e non solo, perché permette di organizzare, gestire,
elaborare dati di qualsiasi genere e rappresentarli graficamente.
In questo percorso, attraverso le schede che ti proponiamo, lo potrai utilizzare
per “programmare” l’applicazione delle formule di matematica che stai studiando.
2
unità 3
UNITÀ 3
Informatica
LE QUATTRO OPERAZIONI E
LE LORO PROPRIETà
1. Le quattro operazioni
Esistono diversi modi per eseguire addizioni, sottrazioni, moltiplicazioni e divisioni con Excel.
1° modo
Si scrivono nelle celle le formule costituite dai simboli:
+ , – , * (moltiplicazione), / (divisione)
e dai numeri con cui si devono eseguire le operazioni. Le formule da utilizzare
sono le seguenti:
=primo addendo+secondo addendo
=minuendo–sottraendo
=primo fattore*secondo fattore
=dividendo/divisore
N.B. Nelle formule di Excel non ci devono essere spazi vuoti tra simboli
e parole che le costituiscono.
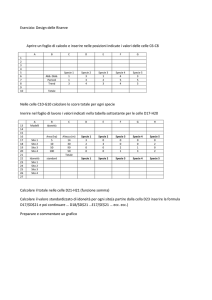
• Riporta sul tuo foglio elettronico:
• scrivi nella cella C2 la formula =56+8;
• premi il tasto invio: compare il numero 64;
• scrivi nella cella D2 la formula =56–8;
• premi il tasto invio: compare il numero 48;
• scrivi nella cella E2 la formula =56*8;
• premi il tasto invio: compare il numero 448;
• scrivi nella cella F2 la formula =56/8;
• premi il tasto invio: compare il numero 7;
• salva con il nome “1°ex sulle 4 operazioni”.
3
Le quattro operazioni e le loro proprietà - unità 3
Informatica
2° modo
Invece dei numeri, nelle formule si possono indicare le celle che li contengono:
=prima cella+seconda cella
=prima cella–seconda cella
=prima cella*seconda cella
=prima cella/seconda cella
Considera ancora la coppia di numeri del precedente esercizio:
• scrivi nella cella C2 la formula =A2+B2;
• premi il tasto invio: compare il numero 64;
• esegui la sottrazione, la moltiplicazione e la divisione scrivendo, di volta in
volta, le formule =A2–B2, =A2*B2 e =A2/B2 rispettivamente nelle celle D2,
E2 e F2;
• salva con il nome “2°ex sulle 4 operazioni”.
2. Formule con riferimenti relativi alle celle
Excel consente con un’unica formula di eseguire consecutivamente più operazioni dello stesso tipo; se poi si sostituiscono con altri numeri i dati iniziali,
viene effettuato il ricalcolo automatico.
• Riporta sul tuo foglio elettronico la seguente tabella e scrivi in C2 la formula
=A2+B2; posizionati poi con il puntatore sul quadratino nero situato in basso
a destra della cella C2;
• quando il puntatore assume la forma a croce, tenendo premuto il pulsante
sinistro del mouse trascina la cella C2 fino a C5;
• rilascia il pulsante del mouse: nelle celle C2, C3, C4, C5 compaiono le somme
27, 90, 114, 224;
4
Le quattro operazioni e le loro proprietà - unità 3
Informatica
• scrivi in D2 la formula =A2–B2;
• posizionati con il puntatore sul quadratino situato in basso a destra della cella D2;
• tenendo premuto il pulsante sinistro del mouse, trascina la cella fino a D5;
• rilascia il pulsante: compaiono le differenze 21, 60, 102, 196;
3. Addizioni di numeri disposti in righe
e/o colonne
Per calcolare la somma di numeri contenuti in più celle consecutive si usa la
seguente sintassi:
=somma(cella iniziale:cella finale).
Per poter utilizzare questa funzione è necessario che le celle formino una zona
rettangolare.
1° MODO
Ogni formula deve essere scritta in una cella che non appartiene alla zona
rettangolare.
Dopo aver scritto la formula all’interno della cella, per avere il risultato è necessario premere il tasto “invio”.
• Per il gruppo di celle in alto a sinistra la formula è: =somma(A3:A11);
• per il gruppo a destra la formula, invece, è: =somma(D4:I4);
• per il gruppo di celle evidenziato in basso: =somma(C10:G14).
5
Le quattro operazioni e le loro proprietà - unità 3
Informatica
2° MODO
Per calcolare la somma di un gruppo di numeri senza digitare la formula (l’insieme delle celle, anche in questo caso, deve però avere una forma rettangolare)
procedi nel modo seguente:
• attiva la cella in cui vuoi che compaia la somma;
• scrivi =somma(
• tenendo premuto il pulsante sinistro del mouse evidenzia la zona rettangolare, nel nostro esempio da A3 a A11 oppure da D4 a I4 oppure da C10 a G14;
• rilascia il pulsante; nella formula, dopo la parentesi, compaiono i riferimenti
della cella iniziale e di quella finale della zona rettangolare evidenziata;
• chiudi la parentesi e premi il tasto “invio”, se vuoi il risultato.
3° MODO
Per calcolare la somma di più numeri che formano una riga oppure una colonna
puoi procedere anche nel modo seguente:
• attiva la cella in cui deve comparire la somma (alla fine di una riga o di una
colonna);
• fai clic sull’icona Somma automatica (simbolo matematico di sommatoria):
in questo modo vengono automaticamente selezionate le celle che contengono
numeri e che precedono, in quel momento, la cella attiva;
• premi “invio” per far comparire il risultato nella cella.
6
UNITà 5
UNITÀ 5
Informatica
I grafici
1. Rappresentazioni grafiche
La procedura per la creazione di un grafico è completamente guidata: è possibile scegliere dalla barra dei Menu le opzioni che permettono di costruire un
grafico come desiderato.
• Con il mouse si selezionano le celle che contengono i dati da rappresentare.
• Si attiva l’opzione Grafici del menu Inserisci.
• Si può scegliere il tipo di grafico e la modalità di rappresentazione, la scelta
dipende da quale aspetto dei dati si vuole evidenziare.
L’Istogramma permette di confrontare elementi diversi oppure di visualizzare
la variazione di dati nel tempo.
N. B. In Excel, con il termine istogramma viene erroneamente indicato anche
l’ortogramma. In realtà l’istogramma è un grafico formato da rettangoli contigui che viene usato per rappresentare dati raggruppati in classi: sull’asse
delle ascisse si riportano i valori degli estremi degli intervalli, sull’asse delle
ordinate sono invece riportate le frequenze assolute negli intervalli stessi.
Anche noi, ogni volta che useremo Excel per costruire i grafici ci adegueremo
alla terminologia usata dal programma.
Il Grafico a linee permette di visualizzare le tendenze nel tempo.
Il Grafico a torta mostra in che proporzione sta ogni elemento rispetto al
totale e si usa quindi per rappresentare dati espressi in percentuale.
Il Grafico a barre consente di confrontare i valori dei dati anziché la variazione nel tempo.
Il Grafico ad area evidenzia le differenze tra vari set di dati in un periodo di tempo.
Il Grafico a dispersione consente di confrontare coppie di valori.
Altri grafici comprende il grafico azionario, ad anello, a bolle o a radar.
• Selezionata la tipologia di grafico, compare sulla barra dei menu la funzione
Strumenti grafico che comprende Progettazione, Layout e Formato
Col sottomenu Progettazione si può intervenire sul Tipo di grafico, sui
Dati, sui Layout grafici e sugli Stili grafici
.
.
Col sottomenu Layout si possono inserire Immagini, Forme e Caselle di testo
(Inserisci), definire i titoli e le voci delle varie etichette (Etichette), scegliere
le varie opzioni per gli Assi, e modificare lo Sfondo.
7
I grafici - unità 5
Informatica
figura d
Col sottomenu Formato si può completare il grafico arricchendolo dal punto
di vista estetico lavorando su Stili Contorni ed Effetti delle forme.
,
2. Rappresentazione grafica dei dati di una
colonna
Seguendo le istruzioni rappresenta graficamente i seguenti dati relativi al peso
in kg di un neonato nelle prime 10 settimane di vita.
• Riporta i dati della tabella sul foglio di Excel e con il mouse evidenzia i dati
delle celle da A3 a B12.
LUCA
settimana
peso (kg)
prima
3,5
seconda
3,3
terza
3,4
quarta
3,65
quinta
3,8
sesta
3,95
settima
4,15
ottava
4,4
nona
4,6
decima
4,75
• Fai clic su Inserisci nella barra dei Menu e seleziona Istogramma, quindi
scegli il primo grafico della colonna 2D (Colonne raggruppate).
• Con la funzione Strumenti grafico puoi perfezionare il grafico come indicato
di seguito.
8
I grafici - unità 5
Informatica
Seleziona Layout e, cliccando sull’icona Titolo del grafico, scegli l’opzione
Sopra il grafico. All’interno dell’area del grafico compare una casella di testo
dove puoi scrivere “CRESCITA CORPOREA DI LUCA”.
9
I grafici - unità 5
Informatica
Sempre in Layout, clicca sull’icona Titoli degli assi e scegli l’opzione Titolo
asse orizzontale principale dalla tendina che si apre e poi Titolo sotto l’asse:
compare una casella di testo dove scrivere “Settimana”.
Rifai la stessa operazione col Titolo asse verticale principale: “Peso in kg”.
Clicca sull’opzione Legenda e scegli Nessuna per disattivare la voce Serie 1
(l’opzione legenda è importante quando ci sono dati da confrontare).
Clicca sull’opzione Assi e seleziona l’Asse
verticale principale e poi, dalla tendina
che si apre, la voce Altre opzioni asse
verticale principale… . Si apre la finestra
Formato asse; in Opzioni assi modifica
l’unità principale cliccando su Fissa e aumentando il valore da 0,5 a 1. Cliccando su
Chiudi l’unità di misura dell’asse verticale
compare con numeri interi.
Col sottomenu Formato, posiziona il
cursore su una colonna dell’istogramma
e clicca una sola volta, le colonne saranno
evidenziate dalle maniglie a pallini; con
l’opzione Riempimento forma cambia
il colore scegliendone uno a tuo piacere.
Ripeti la stessa procedura per l’area del
tracciato (griglia).
Spostando il cursore sui bordi del grafico,
in corrispondenza del puntinato, il cursore cambia forma e, comparendo l’icona a
doppia freccia, puoi modificare le dimensioni del grafico.
10
I grafici - unità 5
Informatica
3. Rappresentazione grafica dei dati di più colonne
Con Excel è possibile costruire grafici in cui le colonne dei dati da rappresentare sull’asse delle ordinate (y) sono più di una come nella seguente tabella.
ANNO
2001
2003
2005
2007
2009
2011
AGRICOLTURA
2
1,9
1,7
1,5
1,4
1,3
INDUSTRIA
6,9
6,8
6,7
6,5
6,4
6,1
ALTRE ATTIVITÀ
11,8
11,9
12,2
12,5
12,7
12,9
• Riporta i dati della tabella su un foglio elettronico.
La procedura per rappresentare graficamente i dati della tabella è simile a
quella considerata negli esempi precedenti; in particolare i valori della prima
colonna vanno rappresentati sull’asse delle ascisse (x) e i valori delle altre tre
colonne sono quelli da rappresentare sull’asse delle ordinate (y).
• Seleziona con il mouse le ultime tre colonne, cioè le celle da B1 a D7.
• Fai clic su Inserisci e scegli il tipo Istogramma con l’opzione Colonne 3D
raggruppate.
• Col sottomenu Progettazione, del menu Strumenti grafico, scegli tra i vari
stili grafici.
• Sempre
dal
sottomenu
Progettazione
clicca
su
Seleziona
dati,
si
apre
la
finestra
Seleziona
origine
dati,
11
I grafici - unità 5
Informatica
alla voce Etichette asse orizzontale clicca Modifica, si apre una finestra Etichette asse, col puntatore del mouse seleziona le celle da A1 a A7, queste compariranno nella finestra Etichette asse, clicca OK 2 volte.
• Perfeziona il grafico mettendo i titoli come già indicato.
12
unità 6
UNITÀ 6
Informatica
LE POTENZE
1. Calcolo del valore di una potenza
Uso di formula con riferimento relativo alle celle
Per calcolare i valori delle prime cinque potenze con base 3:
• intesta la colonna A mettendo la lettera x nella cella A1;
• intesta la colonna B mettendo la scrittura 3x nella cella B1;
• inserisci nelle celle A2, A3, A4, A5, A6 i numeri 0, 1, 2, 3, 4 (sono gli esponenti
da assegnare di volta in volta alla base 3);
• nella cella B2 scrivi la formula =3^A2;
• posiziona il puntatore sul quadratino che si trova in basso a destra della cella,
tenendo premuto il pulsante sinistro del mouse trascina fino alla cella B6;
• rilascia il pulsante del mouse: nelle celle da B2 a B6 compaiono i numeri 1,
3, 9, 27, 81, cioè i valori delle potenze 30; 31; 32; 33; 34.
Uso di formula con riferimento misto alle celle
Per calcolare i valori delle prime cinque potenze con base 3:
• Costruisci la seguente tabella sul tuo foglio di Excel. Per unire più celle e per
colorarle, selezionale e poi clicca rispettivamente sull’icona “unisci e centra”
e sull’icona “colore riempimento”
nella barra di formattazione.
• Scrivi nella cella B4 la formula =A4^$B$2.
Questo è un tipo di formula con riferimento misto alle celle. La prima parte ha infatti
un riferimento relativo alle celle: di volta
in volta nella formula vengono utilizzati i
numeri inseriti nelle celle della colonna A:
da A4 ad A8. La seconda parte ha, invece,
un riferimento assoluto alla cella B2, cioè
nella formula viene sempre utilizzato come
esponente il valore presente nella cella B2.
Quando il riferimento ad una cella è assoluto, alla lettera e al numero che individuano
quella cella si fa precedere il simbolo $.
13
Le potenze - unità 6
Informatica
• Posizionati sul quadratino che si trova in basso a destra della cella B4 e,
tenendo premuto il pulsante sinistro del mouse, trascina la cella fino a B8.
• Rilascia il pulsante del mouse: nelle celle da B4 a B8 compare sempre il numero 1. Perché? ......................................................................................................
...................................................................................................................................
• Nella cella C3 scrivi la formula con riferimento misto =A3^$C$2.
• Posizionandoti poi sul quadratino in basso a destra della cella C3 trascina
fino alla cella C8.
• Rilascia il pulsante del mouse: nelle celle da C3 a C8 compaiono numeri uguali
alle basi. Perché? ......................................................................................................
.....................................................................................................................................
• Nella cella D3 scrivi la formula con riferimento misto =A3^$D$2.
• Riempi tutte le celle della colonna D e poi le altre fino a completare la tabella,
applicando la procedura già illustrata.
Spiega il motivo per cui nella cella B3 non è stato inserito alcun valore: ..........
.....................................................................................................................................
.....................................................................................................................................
14
unità 7
UNITÀ 7
Informatica
DIVISORI E MULTIPLI
DI UN NUMERO NATURALE
1. Calcolo del M.C.D. e del m.c.m.
Calcolo del M.C.D. e del m.c.m. di un gruppo di numeri (1)
Per calcolare il M.C.D. e il m.c.m. dei numeri 80, 128, 176 puoi procedere nel
seguente modo:
• Inserisci nelle celle A2, B2, C2 del foglio di Excel rispettivamente i numeri
80, 128, 176.
• Inserisci nella cella D2 la formula con riferimento relativo alle celle =MCD(A2:C2); altrimenti puoi utilizzare una di queste formule: =MCD(80;128;176)
oppure =MCD(A2;B2;C2). (Per separare i numeri o le celle tra parentesi devi
utilizzare il punto e virgola);
• premi il tasto invio della tastiera: compare il numero 16, cioè il M.C.D. dei
numeri dati.
• Inserisci nella cella E2 la formula con riferimento relativo alle celle =mcm(A2:C2);
anche in questo caso, se non c’è la necessità di calcolare il minimo comune
multiplo di altri gruppi di numeri, puoi utilizzare le formule =mcm(80;128;176)
oppure =mcm(A2;B2;C2).
• Fai clic sul simbolo d’invio o premi il tasto invio: compare il numero 7 040,
cioè il m.c.m. dei numeri dati.
(1): Le funzioni M.C.D. e m.c.m., se non lo sono già, devono essere attivate: in
STRUMENTI cliccare su AGGIUNTE (o COMPONENTI AGGIUNTIVI... nelle
versioni più recenti di Excel) e poi fare clic su STRUMENTI DI ANALISI.
Calcolo del M.C.D. e del m.c.m. di più gruppi di numeri
Per calcolare il M.C.D. e il m.c.m. di più gruppi di numeri, ad esempio quelli
dalla riga 3 alla riga 8, basta utilizzare le formule con riferimenti relativi alle
celle, scritte precedentemente in D2:
• Attiva la cella D2; posiziona il puntatore sul quadratino posto in basso a
destra della cella; tenendo premuto il pulsante del mouse evidenzia le celle
da D2 a D8; quando lascerai andare il pulsante, per ogni gruppo di numeri
comparirà il M.C.D.
15
Divisori e multipli di un numero naturale - unità 7
Informatica
• Procedi nello stesso modo per il calcolo del minimo comune multiplo.
2. Il prodotto di due numeri è uguale al
prodotto del M.C.D. e del m.c.m. degli stessi
numeri
Per verificare la validità di questa affermazione predisponi sul tuo foglio elettronico la seguente tabella:
• Nella cella C2 scrivi la formula =MCD(A2;B2) e trascinala fino alla cella C9;
in questo modo ottieni il M.C.D. di ogni coppia di numeri.
• Analogamente nella cella D2 scrivi la formula =mcm(A2;B2) e trascinala fino
alla cella D9, in quest’altro modo ottieni il m.c.m. di ogni coppia di numeri.
• Nella cella E2 scrivi la formula =C2*D2 e trascinala fino alla cella E9.
16
Divisori e multipli di un numero naturale - unità 7
Informatica
• Nella cella F2 scrivi la formula =A2*B2 e trascinala fino alla cella F9.
• Confronta i risultati delle celle della colonna E con quelli corrispondenti della
colonna F. Come sono?
24
• Scrivi altre coppie di numeri, scelte a piacere, e applica la procedura appena
illustrata.
• L’affermazione fatta all’inizio di questa esercitazione è sempre valida?
17
unità 8
UNITÀ 8
Informatica
LE FRAZIONI
1. La frazione come operatore e frazioni
equivalenti
• Ricopia sul tuo foglio elettronico la seguente tabella, dove con la lettera N si
indica il numeratore della frazione e con la lettera D il denominatore
Ricorda che per applicare una frazione ad un numero o ad una misura si procede così:
1) si divide il numero dato o la misura di una grandezza per il denominatore della frazione;
2) si moltiplica il risultato ottenuto per il numeratore.
3
ai numeri della colonna A scrivi nella cella B3
• Per applicare la frazione
4
la formula =A3/4*3 (A3 è la cella, / è il simbolo che indica la divisione e * è
quello che indica la moltiplicazione ) e poi trascinala fino alla cellaB12.
2 9 4 9 27
,
ai numeri della colonna A.
, , ,
3 8 6 12 24
Confronta i risultati ottenuti nelle colonne B, C, D, E, F, G: cosa osservi? ........
• In modo analogo applica le frazioni
.....................................................................................................................................
Per quale motivo? .......................................................................................................
.......................................................................................................................................
2. Classificazione delle frazioni
Ricorda che:
- le frazioni esprimono delle divisioni, dividendo il numeratore per il denominatore della frazione si ottiene il numero naturale o decimale corrispondente.
- le frazioni che hanno il numeratore minore del denominatore si chiamano
proprie e corrispondono a un numero minore di 1.
- le frazioni che hanno il numeratore maggiore o uguale al denominatore si
chiamano improprie e corrispondono a un numero maggiore o uguale a 1.
18
Le frazioni - unità 8
Informatica
- le frazioni improprie in cui il numeratore è multiplo del denominatore si
chiamano apparenti e corrispondono ad un numero intero.
• Copia sul tuo foglio elettronico la seguente tabella, dove i numeri che intestano le righe (N=) sono i numeratori delle frazioni e quelli che intestano le
colonne (D=) sono invece i denominatori.
• In C3 scrivi la formula =B3/$C$2 e poi trascinala fino a C11: nelle celle
0 1 2
compaiono i numeri naturali corrispondenti alle frazioni , , , ecc. La
1 1 1
formula utilizzata ha nella sua prima parte un riferimento relativo alle celle
(B3) e quindi i numeratori che vengono considerati variano man mano che
la formula viene trascinata: 0, 1, 2, 3, 8, 12 ... . La seconda parte ($C$2) ha
invece un riferimento assoluto alla cella, pertanto il denominatore che viene
considerato è sempre il valore presente in C2, cioè 1.
• Analogamente scrivi nelle celle D3, E3, F3 ... le formule =B3/$D$2 , =B3/$E$2,
=B3/$F$2 ...e poi trascinale rispettivamente fino a D11, E11, F11 ... .
• Osserva con attenzione i quozienti ottenuti ed evidenzia in rosso quelli che corrispondono alle frazioni proprie, in blu quelli che corrispondono alle frazioni
improprie non apparenti e in verde quelli corrispondenti alle frazioni apparenti.
Se hai operato in modo corretto il risultato è il seguente:
Quando una frazione è uguale a 0? ..........................................................................
......................................................................................................................................
Quando una frazione è uguale a 1?.........................................................................
.....................................................................................................................................
19