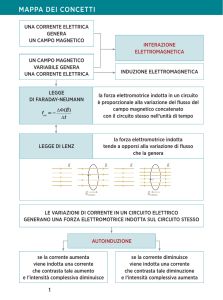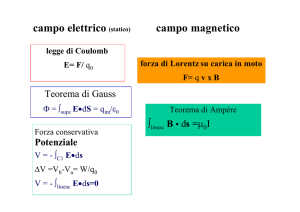
Induzione Elettromagnetica.
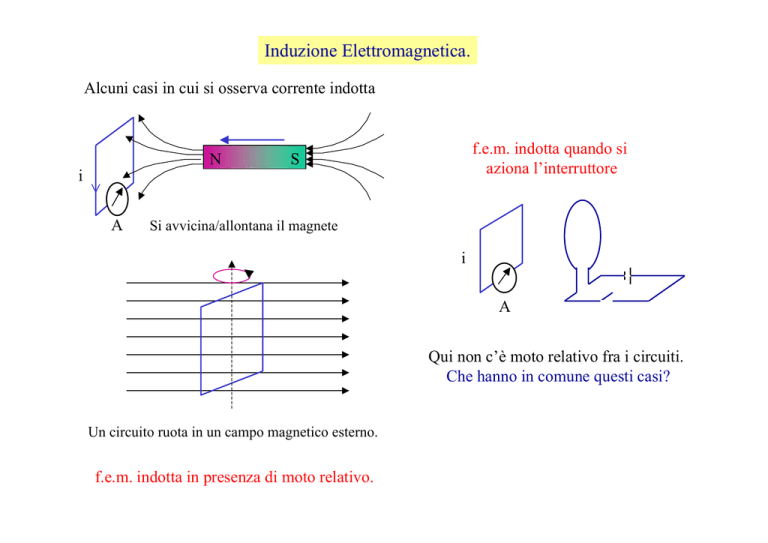
Alcuni casi in cui si osserva corrente indotta
N
f.e.m. indotta quando si
aziona l’interruttore
S
i
A
Si avvicina/allontana il magnete
i
A
Qui non c’è moto relativo fra i circuiti.
Che hanno in comune questi casi?
Un circuito ruota in un campo magnetico esterno.
f.e.m. indotta in presenza di moto relativo.
f.e.m. indotta
La f.e.m. indotta ha le seguenti proprietà:
• aumenta all’aumentare della velocità relativa o alla rapidità dei cambiamenti
• cambia segno se si inverte il verso del moto, o fra apertura e chiusura dell’interruttore
• aumenta all’aumentare del campo B inducente (magnete “più forte” ...)
• il verso della corrente/fem indotta è tale da opporsi alla causa che lo produce
In tutte le esperienze precedenti cambia il flusso del campo B concatenato al circuito.
Tutte le osservazioni si riassumono nella:
ε
IND
=−
dΦ B
dt
Legge di Faraday-Neumann
ΦB è il flusso concatenato al circuito
Punti da chiarire:
• che si intende per flusso concatenato ad un circuito?
• qual è il significato del segno “-” ?
Flusso del campo magnetico concatenato ad una linea.
A) Flusso attraverso una superficie piana (aperta)
r r
dΦ B = B ⋅ n dS
[Φ B ] = Tm 2 =
r r
Φ B (S ) = ∫ B ⋅ n dS
dS
normale alla superficie
indica il verso prescelto
J
= Vs = Wb
A
♦ si è sempre parlato di flusso attraverso una superficie
♦ esistono infinite superfici aventi per limite una linea chiusa (circuito) (ad es. S1 e S2)
si trova che
linea chiusa
γ
S1
Φ B (S 1 ) = Φ B (S 2 )
il flusso non dipende dalla superficie considerata (purché delimitate
dalla stessa linea). S1 e S2 delimitano una superficie chiusa, quindi:
Φ B (S ) = Φ B (S 1 ) + Φ B (S 2 ) = 0
S2
I due flussi sono uguali in modulo. Lo sono anche in segno se
la normale alla superficie (aperta) viene scelta in modo opportuno.
Induzione E.M
La convenzione è che il verso positivo della f.e.m. e quello di ΦB siano legati fra loro dalla
regola della mano destra.
La scelta del verso positivo è arbitraria, ma non si possono scegliere indipendentemente.
verso positivo di ΦΒ
verso positivo della f.e.m.
E
In questo senso si deve interpretare il segno: un aumento del flusso ΦB in figura induce
una corrente diretta in verso orario e viceversa.
Inoltre: la corrente (f.e.m.) indotta è tale da opporsi alla causa che la produce.
ii
N
N
S
S
i indotta si oppone alla variazione di ΦB e produce una forza repulsiva sul magnete che si avvicina
Come si spiega la presenza di correnti indotte?
A) Circuito mobile in un campo B costante
v
iIND
una sbarretta scivola su guide conduttrici
in campo B uniforme
sulle carica di conduzione
agisce una forza di Lorentz,
che produce una corrente
nel verso di FL
B) Circuito fisso in un campo B variabile
la variazione di B genera un campo elettrico
(indipendentemente dal circuito, anche nel vuoto)
Il campo elettrico indotto, a differenza del
caso elettrostatico, non è conservativo.
La circuitazione di EIND non è nulla, ma è
uguale alla f.e.m. indotta
r r
ε = ∫ E⋅ ds = − dΦ
dt
Il betatrone
v
FL
Espansioni polari di un
magnete. B uniforme
ma variabile
linee di forza
di E indotto
Flusso concatenato ad un circuito.
A) Flusso di un campo B prodotto da un altro circuito
B entrante
i1
i2
Φ B 2 ∝ i1
Φ B 2 ∝ M i1
M: coefficiente di mutua induzione
o mutua induttanza
M>0 o M< 0
Esempio: trasformatore.
B) Flusso di un campo B prodotto dal circuito stesso.
Φ B 2 ∝ i2
Φ B 2 ∝ Li 2
[M ] = [L ] =
L: autoinduttanza
(sempre L>0)
Wb
Vs
=
= Ωs = H
A
A
spira circolare
Alcune conseguenze dell’autoinduzione.
ε
R
i
alla chiusura del circuito la corrente
non passa immediatamente al valore
finale, a causa della f.e.m indotta
ε/R
t
i
ε
all’apertura del circuito, la corrente
non va immediatamente a zero,
sempre a causa della f.e.m. indotta
R
Schematicamente, il circuito
si rappresenta così
ε
t
Notare che, alla chiusura, ε > Ri quindi
ε i > Ri
R
i=ε/R
2
il generatore eroga più potenza di quella
dissipata nella resistenza.
Dove finisce questa energia?
L
Si può provare che è immagazzinata nel campo magnetico
ed è restituita all’apertura del circuito.
Al campo magnetico è associata
una densità di energia:
uB =
1
B2
2µ 0
nel vuoto
Effetti del campo elettromagnetico di bassa frequenza
A livello atomico-molecolare (Chimica e Biologia) le forze dominanti sono elettromagnetiche.
(
r
r r r
F = q E+v×B
)
forza di Lorentz
I campi E.M. esterni possono influenzare i processi biologici? Effetti (negativi) sulla salute?
Per l’ ICNIRP (International Commission on Non-Ionizing Radiation Protection)
(Health Phys. 75 (4) 442, 1998)
ν< 100kHz. Assorbimento di energia trascurabile
100kHz<ν<20MHz assorbimento cresce con ν, importante per gambe e collo
20MHz<ν<200MHz Assorbimento distrib. su tutto il corpo
300MHz<ν<10GHz Assorbimento localizzato
ν>10GHz Assorbimento superficiale.
In generale si sono osservati effetti per forti assorbimenti di energia, corrispondenti ad aumento di
temperatura di 1°C.
Per basse frequenze (ELF) studi di laboratorio evidenziano effetti (non necessariamente nocivi)
per B>10mT e E>100mV/m
Nel caso dei 50/60Hz si discute dal lavoro di Wertheimer e Leeper, Am.Jour.Epid. 109, 273 (1979)
Effetti del campo elettromagnetico di bassa frequenza
Il caso ν=50/60Hz.
A ν=50Hz la lunghezza d’onda EM è λ = c/ν = 6000 km
Si possono trattare i campi generati ad es. da un filo percorso da corrente come “quasi statico”:
µ 0 i (t )
B(t ) ≅
2π r
Considerazioni qualitative di tipo fisico (ordini di grandezza) sui possibili effetti del campo EM a 50Hz.
• In prossimità di elettrodotti esiste campo E e B
• Il corpo umano è un conduttore: ρ=1Ωm
-
EEXT
+
EINT
- +
+
+
+
Se il campo fosse statico, EINT=0
Campo E esterno (in assenza del conduttore)
Il corpo umano è conduttore (ρ=1Ωm).
In realtà se EEXT oscilla, le cariche indotte oscillano: c’è una corrente. Quindi un campo elettrico E=ρJ
Effetti del campo elettromagnetico di bassa frequenza
E INT =
Si dimostra che
3
Kε 0ωρE EXT
2
50Hz
K: costante numerica (K=1 per una sfera) ω = 2πν=314 s-1. Il risultato è:
E INT ≤ 10 −7 E EXT
EINT fortemente ridotto: anche EEXT=104 V/m dà EINT=1mV/m
Lo schermaggio elettrostatico è ancora molto efficiente.
Il campo magnetico però può penetrare, e generare un campo elettrico indotto.
EB =
1
BEXT ω r
2
r è una dimensione caratteristica,
dell’ordine di 10cm.
Quanto vale BEXT?
Nelle abitazioni tipicamente BEXT < 0.1µT
Presso Elettrodotti fino a 100µT, ma diminuisce rapidamente con la distanza (v. esempi)
Un’esposizione a BEXT < 5µT non dovrebbe creare problemi.
Effetti del campo elettromagnetico di bassa frequenza
Altri effetti.
EINT
membrana dilipidica. Spessore d=7nm Alta resistività.
ECEL
La caduta di tensione ∆V si concentra nella membrana
Cellula (1-100µm)
Se EINT=1mV/m EMEM=10V/m (valori fisiologici 107V/m)
ECEL=10-5 EINT
Valori tipici di ∆V indotto nella cellula non superano 0.1 µV,
minori delle fluttuazioni intrinseche dell’ordine di 3µV
Tali campi sono anche minori dei campi di origine fisiologica: un elettrocardiogramma
fornisce ∆V = 1mV a 0.5 m di distanza e il campo elettrico può raggiungere anche 1V/m
in prossimità del cuore.
IN CONCLUSIONE
Non c’è evidenza sufficiente di danni provocati dai campi EM della rete elettrica
• Anche i risultati positivi non forniscono un quadro coerente:
• ad es. non è mai stata dimostrata una relazione dose-risposta
• Manca un meccanismo microscopico credibile.
Secondo l’ ICNIRP (www.icnirp.de)
Al 1998 solo 5 studi su 15 riportano un maggior rischio in relazione ad una maggiore
esposizione al campo EM
Alcuni degli studi più rigorosi non mostrano dipendenza
Anche quando c’è correlazione, non c’è andamento chiaro in funzione del campo
(es. correlaz. B>0.2mT, che però diminuisce per B maggiori)
Gli studi di laboratorio su cellule o volontari evidenziano effetti solo per campi molto
più intensi (B>10mT, E~100mV/m
“Non c’è attualmente un’evidenza convincente di effetti cancerogeni di questi campi”.
Inutile dire che questi argomenti sono fortemente contestati dagli ambientalisti
(v. www.verdinrete.it/ondakiller )
rete
telefonini
6V/m
Linee guida ICNIRP
(adottate UE 1999)
E l’Italia?
10µT
3µT