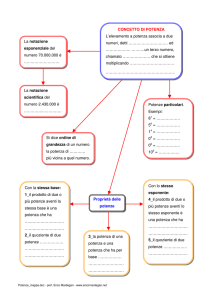
5. Proprietà e calcolo di limiti
Se vogliamo andare oltre le funzioni elementari e calcolare limiti di funzioni più complicate
abbiamo bisogno di qualche proprietà in più. Anzitutto possiamo combinare i limiti che conosciamo
già: per esempio si ha
lim( x 2 + 2 x) = 1 + 2 = 3
x →1
ossia se dobbiamo calcolare il limite di una somma, basta fare la somma dei limiti e così via. Più
precisamente:
Proposizione 1. Sia f → L1 e g → L2 per x → x0 (oppure per x → x0− , x → x0+ , x → −∞ ,
x → +∞ ) . Allora
per x → x0 (oppure per x → x0− , x → x0+ , x → −∞ , x → +∞ )
Ad esempio, dimostriamo la proprietà per la somma f + g: sappiamo che f → L1 e g → L2 , quindi
per ogni ε possiamo trovare δ tale che
e queste disuguaglianze si possono scrivere anche così:
Sommando le due disuguaglianze otteniamo
e questo vuol dire esattamente f + g → L1 + L2 per x → x0 .
Esempio 1. La proprietà precedente implica subito che per ogni polinomio P(x) si ha
Ad esempio
Osservazione 1. Le proprietà precedenti si possono applicare senza problemi quando L1 ed L2
sono numeri reali. Ma è facile verificare che molte proprietà si estendono anche al caso di limiti
infiniti. Esaminiamo i casi possibili. Cominciamo dalla somma:
1
Resta escluso il caso +∞ − ∞ : in questo caso non si può dare una regola generale perchè il risultato
può essere diverso a seconda delle funzioni, e in questi casi si dice che
+∞ − ∞ è un limite indeterminato
Per capirlo basta un esempio banale: i due limiti seguenti sono entrambi del tipo +∞ − ∞ , ma il
risultato è diversissimo:
Per quanto riguarda il prodotto abbiamo
Anche per il prodotto scopriamo che il caso
∞ ⋅ 0 è un limite indeterminato
Infine per il rapporto abbiamo
nei punti 3) e 5) abbiamo usato la notazione
e
Per il rapporto scopriamo che
∞
0
e
sono indeterminati
∞
0
2
Proposizione 2 (Il Teorema dei Carabinieri). Se f(x) e h(x) tendono allo stesso limite L per x → x0
e la funzione g(x) è compresa tra di esse, ossia
allora anche g → L per x → x0 .
Dimostrazione. Dall'ipotesi sappiamo che: per ogni ε esiste δ tale che
per 0 <| x − x0 |< δ ; quindi abbiamo anche
e in particolare
per 0 <| x − x0 |< δ , e questa è proprio la tesi.
Proposizione 3. (Permanenza del segno). Se una funzione f è positiva ossia f ( x) ≥ 0 , e tende ad un
limite L per x → x0 , allora anche L ≥ 0 . In altri termini: il limite di una funzione positiva è positivo
(e il limite di una funzione negativa è negativo).
L
Dimostrazione. Se per assurdo fosse L < 0, scegliamo ε = e proviamo ad applicare la definizione
2
di limite: deve esistere δ tale che
per 0 <| x − x0 |< δ . Ma la seconda disuguaglianza implica che
e questo è assurdo perchè sappiamo che la funzione è positiva.
Calcolo di limiti
Esempio 3.5.1. Ripassiamo rapidamente i limiti fondamentali che seguono subito dalla definizione
delle funzioni elementari. Per le potenze con esponente positivo abbiamo
e naturalmente anche
3
Inoltre per le potenze pari
mentre per le potenze dispari
Passiamo alle potenze negative: si ha subito per ogni n
e anche
Inoltre per le potenze pari
mentre per le potenze dispari
Per l'esponenziale abbiamo
Questo è lo stesso comportamento di tutte le funzioni esponenziali con base maggiore di uno:
mentre se la base è minore di 1 il comportamento si rovescia:
La funzione log x è definita solo per x > 0 e si ha
4
Esempio 2. Molti limiti si calcolano subito utilizzando le regole viste finora. Ad esempio, proviamo
a calcolare i limiti
Per il primo, grazie alla proposizione sulle operazioni fra i limiti, basta calcolare il valore della
funzione nel punto:
Per il secondo basta osservare che il denominatore
tende a +∞ , e quindi abbiamo subito
Infine dato che
abbiamo anche
Esempio 3. Dato il polinomio
calcolare i limiti
I primi due sono semplicissimi: il limite è uguale al valore di f nel punto in cui si fa il limite. Infatti,
usando i risultati noti per le operazioni sui limiti,
5
Analogamente
Il terzo limite è indeterminato, infatti −4x3 → −∞ , mentre 2x 2 → +∞ ; ma possiamo riscrivere la
funzione così:
e ora vediamo che
e quindi per le regole note
(abbiamo ottenuto una forma del tipo ( +∞ ) ⋅ ( −4 ) che non è più indeterminata!).
L'ultimo limite si calcola allo stesso modo:
(qui otteniamo una forma del tipo ( +∞ ) ⋅ ( −4 ) ).
Esempio 4. Calcoliamo il limite del rapporto di due polinomi:
Notare che sia il numeratore che il denominatore tendono a +∞ , quindi abbiamo una forma
indeterminata. Ma i due infiniti sono “dello stesso ordine”, quindi il limite è infinito: per vederlo
mettiamo in evidenza il grado massimo al numeratore e al denominatore e semplifichiamo:
6
per x → +∞ .
Se invece i due polinomi hanno grado diverso, il rapporto sarà dominato dal grado
maggiore. Ad esempio:
perchè il numeratore ha grado più alto. Come regola empirica possiamo scrivere:
e quindi
Analogamente, possiamo dire che
ossia
7