i numeri - IIS Gadda Fornovo

I NUMERI
Cal
col
oi
n N,Z,Q R
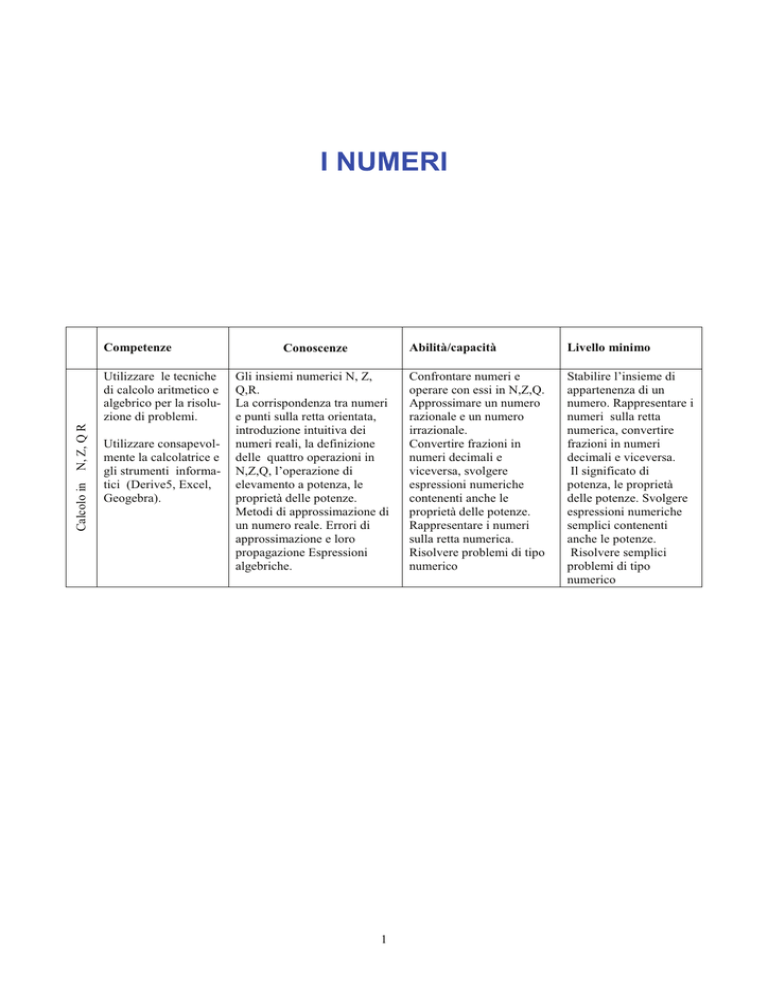
Competenze
Conoscenze
Gl
ii
nsi
eminumeri
ciN,Z,
Q,
R.
Lacorri
spondenzat
ranumeri
epunt
isul
l
aret
t
aori
ent
at
a,
i
nt
roduzi
oneintui
t
ivadei
i
,l
adefini
zi
one
Ut
i
l
i
zzareconsapevol- numerireal
l
e quat
t
rooperazi
onii
n
ment
el
acal
col
at
ri
cee del
Z,
Q,l’operazi
onedi
gl
ist
rumentii
nforma- N,
evament
oapot
enza,l
e
t
i
ci(Deri
ve5,Excel
, el
propri
et
àdel
l
epot
enze.
Geogebra).
M et
odidiapprossimazi
onedi
unnumeroreal
e. Erroridi
approssimazi
oneel
oro
propagazi
oneEspressi
oni
al
gebri
che.
Ut
i
l
i
zzare l
et
ecni
che
dical
col
oari
t
met
i
coe
al
gebri
coperl
ari
sol
uzi
onediprobl
emi
.
1
Abilità/capacità
Livello minimo
Confront
arenumerie
operareconessii
nN,
Z,
Q.
Approssimareunnumero
razi
onal
eeunnumero
i
rrazi
onal
e.
Convert
i
refrazi
oniin
numeridecimal
ie
vi
ceversa,svolgere
espressi
oninumeri
che
cont
enent
ianchel
e
propri
et
àdel
l
epot
enze.
Rappresent
areinumeri
sul
l
aret
t
anumeri
ca.
Ri
solvereprobl
emidit
i
po
numeri
co
St
abi
l
i
rel
’insi
emedi
appart
enenzadiun
numero. Rappresent
arei
numerisul
l
aret
t
a
numeri
ca,convert
i
re
frazi
oniinnumeri
decimal
ievi
ceversa.
Ilsi
gni
fi
cat
odi
pot
enza,l
epropri
et
à
del
l
epot
enze. Svol
gere
espressi
oninumeri
che
sempl
i
cicont
enent
i
anchel
epot
enze.
Ri
solveresempl
i
ci
probl
emidit
i
po
numeri
co
PROBLEM A
Trat
t
odall
i
brodiM al
baTahan–L’uomochesapevacont
are Adri
anoSal
aniEdi
t
ore -2002
Trefratellistavanolitigandoperlaspartizionedell’ereditàlasciatadalpadre: sitrattavadi
suddividere35 cammellisecondoleindicazionidelvecchio:
alprimogenitolametàdeglianimali(17 cammelliemezzo),
alsecondogenitounterzo(piùdi11 cammellimamenodi12),
alterzogenitosolounnono(piùdi3 cammellimamenodi4).
L’abileBeremizintervenneerisolseladisputainquestomodo: aggiunseilpropriocammelloai
cammellideitrefratelliequindieffettuòlaripartizionedei36 animali:
alprimogenitoandòlametàdeglianimali(18 cammelli),
alsecondogenitounterzo(12 cammelli),
alterzogenitosolounnono(4 cammelli).
Ifratellifuronocosìassaisoddisfattidellapropriapartedieredità: aciascunodiessispettavapiùdi
quantopensasse.
Beremizsiripreseilpropriocammelloe,poichéneavanzavaancorauno,lopresecomecompenso
peraverrisoltoconsoddisfazionedituttiilcompl
i
catoproblemadell’eredità.
Comeèpossibiletuttoci
ò?
Discussioneinclasse… … .
LABORATORIO 1 L’unitàfrazionaria
L’usodellefrazionieragiànotoaltempodegliegiziederalegatoessenzialmentealproblemadella
misurazionedeiterreniperridefinireiconfinideivaricampiinondatidallepienedelNilo.
Ognifrazionevenivatrasformatanellasommadialtrefrazionisempreconnumeratore1: cioèin
sommadiunitàfrazionarie.
Esempio:
5 1 1
= + ilcalcoloeramoltocomplicato!
8 2 8
1
1
cichiediamosubitodichecosa? Infattilafrazione acquistasignificato
2
2
seèriferitaadunaprecisagrandezzaecichiediamoqualèl’unitàdimisurachevogliamodividere
induepartiuguali. Osserviamolaseguentetavola:
Quandoleggiamo
2
Tavola delle frazioni : le unità frazionarie
unità
1/2
1/2
1/3
1/4
1/5
1/6
1/7
1/8
1/3
1/3
1/4
1/4
1/5
1/5
1/6
1/7
1/8
1/5
1/6
1/7
1/8
1/6
1/6
1/7
1/8
1/7
1/8
1/7
1/8
1/8
1/4
1/5
1/6
1/7
1/8
Selezioniamosoloalcunerighe.
unità
1/2
1/2
1/4
1/8
1/4
1/8
1/8
1/4
1/8
1/8
1/4
1/8
1/8
1/8
Osserviamoche:
Osservandolatabella ricaviamolefrazioniequivalenti
1 2 4
= = =…
2 4 8
Sempreconlatabellafacciamolesommedifrazioni,infatti:
1 1 3
+ =
2 4 4
perché è
Nascelaregoladellasommadifrazionimedianteilminimocomunemult
iplo.
3
2 1 3
+ =
4 4 4
Problemi di base
3
P1) Determinarei diunagrandezza.
4
Significadivideretalegrandezza(cherappresentailnostrointero) inquattro partiuguali
(denominatore: dichiarainquantepartiugualidivido)eprenderne3 parti(numeratore).
Classe 2°media
3
Procedimento : Sedevocalcolare i di64 € eseguo:
4
1
3
64:4 =16 (cheè dell’intero)→ 163 = 48 € (essendo <1
4
4
Classe 3°media o 1°superiore :
Procedimento :
x=
48 < 64!)
3
⋅ 64 = 48 €
4
5
P2) Determinarei diunagrandezza.
4
5
Procedimento: Sedevocalcolare i di64 € eseguo:
4
1
5
64:4 =16 (cheè dell’intero)→ 165 = 80€ (essendo >1 allora 80>64!)
4
4
5
Classe 3°media o 1°superiore Procedimento : x = 64 = 80€
4
1
P3)Giannidice che100€ rappresentano dellasommachehaintasca.
4
Quantopossiede? Ha piùomenodi100€?
Classe 2°media
Classe 2°media :
(Lasommachehaintascaèl’unitàfrazionaria,valeadirequattrovolte100€).
Procedimento :
100 4 = 400€
Giannipossiede400€
Classe 3°media o 1°superiore Procedimento
Indicocon xquellochehaintascapercui
1
100=
x → (2°principiodiequiv.)→ 100 4 =x x = 400.
4
18
P4)M arcopossiede162 figurinecherappresentanoi diquellechepossiedePaolo.
5
QuantenepossiedePaolo?
.
Classe 2°media Procedimento:
162 :18 = 9 (cioè
1
5
diciòchehaPaolo) → 9 5 = 45 figurine(cioè ,l’unità)
5
5
Classe 3°media o 1°superiore Procedimento :
4
18
x
5
(2°principiodiequiv. ) 162⋅5 = 18x
162 ⋅ 5
(2°principiodiequiv.)x =
= 45. Paolopossiede45 figurine.
18
x = n°figurinediPaolo. 162 =
P5)Unpadreeisuoiquattrofiglisidividonolacifra guadagnataallafinediunalungagiornata
1
dilavoro. Alpadrespetta dellasommaelaparterimanentevienedivisatraisuoifigliinparti
3
uguali.Qualefrazionedellasommaspettaaciascunfiglio?
A)
1
2
B)
1
3
C)
1
4
D)
1
6
1
1 − : 4 .
3
Scrivol’espressionecherisolveilproblema
1
Comemodellodiequazi
one possiamoscrivere 1 − = 4 x indicandoconx lafrazione
3
richiesta.
Iseguenti laboratori sono stati in parte rielaborati partendo dalle due attività proposte
dal corso di formazione mat@ bel :
“Frazioni in movimento” e “Dalla frazione al numero decimale”.
Laboratorio 2
Le frazioni e le loro operazioni
Descrizione dell’attività
M odello
Utilizzareunmodellodasuddividereinparticongruenti:
•
•
•
unameladaaffettareconiltagliamelachesuddividein8 particongruenti,
uncartoncinodiformarettangolaredasuddividereinrettangolinicongruenti,
un cerchiodasuddividereinsettoricongruenti.
Sipartedaunasuddivisionein 8 partidelmodelloscelto.
5
Figura 1: Un cerchio suddiviso in settori congruenti.
Rappresentazione sulla retta e individuazione delle frazioni equivalenti
1 2 3
8
Sirappresentanosullarettaorientata: ; ; … finoa =1.
8 8 8
8
Siindividuanolefrazioniproprieequellaapparente.
Siindividuanolefrazioniequivalenti:
1 4 2 1 2 3 6
= = ; = ; = .
2 8 4 4 8 4 8
Somma di frazioni
Sommadifrazionidaeseguireconilmodello
1 1
1 1
1 3
+ = ; + = ; + = .
2 4
4 8
2 8
Frazioni improprie
Siprocedeaggiungendounaltromodellougualesempresuddivisoin8 parti. Siosservanoesi
16
rappresentanosullarettalefrazioniimpropriecompresetra1 e2 e lafrazioneapparente .
8
Somma di frazioni
5 7
1
1
+ = ; 1 + = ; 1 + = 8 8
8
2
.
Osservarechesipuò calcolarecondenominatore8 maanche4 o2 echeconilmcm inumerial
numeratoresonoipiùpiccoli.
5 1
+ = .
4 8
Sottrazione di frazioni
Sottrazionedifrazionidaeseguireconilmodello (lasottrazionepuòessereintesacometoglieredal
minuendoinpossessodiunalunnoilsottraendoconsegnandoloadunaltro).
6
3 1
3
− = ; 2 − = .
4 4
4
1 2
Ilcasoincuisihaunnumeronegativosipuòconsiderarecomeundebito − =
8 8
Prodotto di frazioni
Prodottodifrazionidaeseguireconilmodello
1
2 ⋅ = (faccioildoppiodiunmezzo)
2
1
2
⋅ 2
(facciolametàdi2)
confrontoiduerisultati
1 1
1
1
⋅ = (facciolametàdi )Confrontareilrisultatocon
2 4
4
4
2 3
3
3
⋅ = (prendo dividoin3 eprendo2 mucchietti)Confrontareilrisultatocon
3 4
4
4
5 3
3
⋅ = (laprimafrazioneèimpropria,prendo dividoin2 eprendo5 mucchiettiugualiaquelli
2 4
4
3
ottenuti). Confrontareilrisultatocon
4
Frazioni decimali
Sisuddivideunnuovomodelloin10parti.
Rappresentazione sulla retta
Sirappresentanosullarettaorientata:
1 2 3
10
; ; … finoa =1.
10 10 10
10
Particolaresignificato assumelasuddivisionedell’intervallo unitario in diecipartiperchépermette
dieffettuareuncollegamentoconlascritturaposizionaledecimaleelarappresentazionedeinumeri
decimalisullaretta.
Osservare la corrispondenza tra le frazioniaventicome denominatore 10,base dinumerazione
usata,ed inumeridecimaliaventiuna sola cifra dopo la virgola,verificando,eventualmente,
l’equivalenzaeffettuandoladivisionetrailnumeratoreeildenominatoreditalifrazioni.
7
Ingrandendo il primo decimo e suddividendo questo intervallo in successive dieci parti, si
otterrannoaltridiecipuntiacuisaprannoattribuireduescritturediverse: 00,
01 0,02 0,
03 0,
04 0,
05
0,
06 0,
07 0,
08 0,
09 0.1
Ripetendoildiscorsosipotrannoeffettuareconsiderazionisulconcettodidensitàdellaretta
numerica.
Riconoscimento di frazioni equivalenti
Calcolareilquozientefrailnumeratoreeildenominatoredellefrazioni
3
6
9
= ; = ;
= .
4
8
12
Esistonofrazioniapparentementediversemaaventilostessopuntocorrispondentesullaretta.
8
Rappresentazione sulla retta numerica di frazioni di unità –metodo grafico
LarettaAB elarettaA’B’sono parallele,cosìcomelarettaCB elarettaC’B’quindiitriangoli
ABC e A′B ′C ′ sonosimili;dalfattocheA’C’=1discendeilmetodoperlarappresentazionedelle
frazionidell’unitàsullarettanumerica.
In assenzadelconcetto disimilitudinedifigure piane,questo esercizio può essere somministrato
senzadimostrazione,comestimoloall’osservazioneecomeeserciziodidisegnogeometrico.
Figura 2: M etodo grafico perrappresentare sulla retta numerica le frazioni di unità
9
ESERCIZIDIBASE con DERIVE 6
10
Delleseguentiespressionicomparesoloilrisultato
11
Laboratorio 3
Dalla frazione al numero decimale
Descrizione dell’attività
Ilpercorso procede per mezzo di domande alle quali si cercheràdi rispondere usando gli strumenti
(concettuali e di calcolo)a disposizione degli studenti.Si puòsuddividere la classe in piùgruppi di
lavoro e far consegnare la risposta scritta ad ogni gruppo suun foglio per poi commentare insieme
i risultati (si può eventualmente assegnare un punteggio ad ogni gruppo per ciascuna risposta
corretta).
3
Domanda 1: Come si trasforma la frazione in numero decimale?
8
Commento: Sipuòfarnotarecheilrisultato0,
375 èunnumerodecimalelimitato.
***
Domanda 2: Quale numero decimale si puòassociare a
7
?
12
Commento: (numero decimale periodico)se un risultato ha molte cifre decimali,quante cifre si
devono scrivere? Si possono anticipare i concetti di approssimazione e di risultato esatto
(eventualmente indicato con la frazione stessa),facendo notare quando si fa uso dell’uno o
dell’altro.
***
Domanda 3: Esprimere come frazione il numero decimale limitato 3,
14
Commento: unnumerodecimalelimitatoèespressionediunafrazionechehaperdenominatoreuna
potenzadi10. Tratuttel
efrazioniequivalenticorrispondentia3,
14 quellacon iterminiminimiè
157
.Siosserverà che la riduzione è ottenuta dividendo numeratore edenominatore perilloro
50
M CD.
***
Domanda 4: completare la tabella che segue eseguendo i calcoli a mano.
n
m
7
20x3 = 60
17
5 x11 = 55
23
200
18
25
Numerodecimale
n
corrispondentea .
m
7
=… … … … …
60
17
= … … … … ..
55
23
= … … … … ..
200
18
=… … … … …
25
12
Ildenominatoreha
Ilnumerodecimaleè
unfattore
limitato?
diversoda2 eda5?
Vero
Falso
Vero
Falso
24
= … … … … ..
37
***
Domanda 5: Osservando la tabella,in quali condizioni una frazione ridotta ai minimi termini
èespressa da un numero decimale limitato?
24
37
Commento
E’già stato ricordato che un numero decimale limitato è espressione di una frazione che ha per
denominatore una potenza di 10.
Sirichiameràesplicitamentel’unicità della scomposizione in fattori primi deinumerinaturali, si
faràosservarechedaquestedueaffermazionisiricavalaseguente:
un numero decimale limitato è espresso da una frazione ridotta ai minimi termini il cui
denominatore contiene soltanto come fattori primi il2 o il5(o entrambi),unici fattori primi dell
a
base 10.
Infatti, il denominatore della frazione ridotta deve essere necessariamente un divisore di
un'
opportuna potenza di10,denominatore della frazione che siottiene direttamente dalnumero
decimalelimitato.
Sipotrà anche esprimere questa proprietà nella forma contronominale che forse risponde più
direttamentealladomandaposta:
se ildenominatore di una frazione ridotta ai minimi termini contiene come fattore primo un numero
diverso da 2e da 5,allora ilnumero decimale corrispondente non èlimitato.
***
L’insegnantepuòproporreun'
attivitàconl’usodiunfoglioelettronicoodiunacalcolatriceincui
fareinserirevariefrazioninellatabella. Sipossonopoimettereinsiemeirisultatideivarigruppi
perfareconsiderazioniepergiungereallarispostadelladomanda7.
Domanda 6: Esprimere una frazione come numero decimale,dopo averla ridotta ai minimi
termini,e poi scomporne il denominatore in fattori evidenziandone la potenza di 2,la potenza
di 5e l’eventuale altro fattore primo con 10.
Frazione
Frazioneridottaai
minimitermini
n. decimale
12
15
13
Scomposizioneinfattori
deldenominatore
Domanda 7: Che relazione c’ètra il denominatore di una frazione ridotta ai minimi termini e
il numero di cifre della parte frazionaria della sua rappresentazione decimale,quando questa
èlimitata?
Commento:
Sifarà osservare che inumeridecimalisono limitatidato che corrispondono a frazioniicui
denominatorihannosolo2 o5 comefattoriprimi.
Ilnumero delle cifre della parte frazionaria delnumero decimale è uguale almaggiore tra gli
esponentidellepotenzedi2 edi5 nellascomposizionedeldenominatore.
***
Domanda 8:Quando termina una divisione? Come sono i resti calcolati nel procedimento della
1
divisione rispetto al divisore?Infine trasformare in decimale .
7
Commento: In una divisione tra due numeri naturali si possono presentare solo due casi:
1. sitrovailresto0: inquestocasoilprocedimentotermina,ilnumerodecimaleèlimitato,
2. siripeteun resto giàtrovato,infattiirestipossibilisonoin numero finito. In questo caso il
procedimentodelladivisioneèciclico(operiodico).
***
Larispostaalladomanda5 ciharicordatochese ildenominatore di una frazione ridotta ai minimi
termini contiene un fattore primo diverso da 2 e da 5,allora ilnumero decimale corrispondente
non èlimitato.
Domanda 9: Quando la frazione ridotta ai minimi termini ha al denominatore un fattore
diverso da 2e da 5,com’èil numero decimale che le corrisponde?
Commento: ad una frazione ridotta ai minimi termini,ilcui denominatore contenga fattori primi
rispetto a 10,corrisponde un numero decimale periodico.Ilnumero di cifre delperiodo èminore
deldenominatore della frazione data.
***
Domanda 10: Calcolare il numero decimale corrispondente alle seguenti frazioni
5 7 32 275
, , ,
.
13 17 49 509
Commento:
M entreperleprimedueilcompitoèancorafattibile,anchesepiuttostonoioso(laprimaha6 cifre
diperiodo,lasecondaneha16),leultimeduesonoimproponibiliperuncalcolomanuale. Infattila
terzafrazionegeneraun numero decimalecon un periodo di42 cifreelaquartauno di508 cifre.
L’insegnante metterà in evidenza che l’algoritmo che calcola tutte le cifre della rappresentazione
decimalediunafrazioneridottahatermineneiduecasi:
- setrovacomeresto0: inquestocasoilnumerodecimaleèlimitato;
- se trova nuovamente ilresto con cuiha inizio ilperiodo. In questo caso occorre stabilire
quandoiniziailperiodoperfissareilrestochesaràusatocomeconfronto.
***
14
Domanda 11: Data una frazione ridotta ai minimi termini,quante sono le cifre della sua
rappresentazione decimale?
Commento
A questadomandasiègiàrispostonelladomanda5 perinumeridecimalilimitati. Nelladomanda
7 siètrovato un limiteperilnumero dellecifredelperiodo diun numero decimaleillimitato: tale
numero è minore del denominatore della frazione ridotta ai minimi termini che lo genera.
Siricordachelapartedicifredopo la‘virgola’cheprecedeilperiodo sichiamaantiperiodo. Il
numero dicifre dell’antiperiodo è dato dalla stessa regola che è stata descritta perle cifre del
numerodecimalelimitato:
ilnumero delle cifre dell’antiperiodo èuguale almaggiore tra gli esponenti delle potenze di 2e di
5nella scomposizione deldenominatore.
***
Verifica
1) Scegl
iendo come unitàgraf
ica un segmento,rappresenta l
ef
razioni seguenti.
3 1 5 2 6 4
; ;
; ; ;
8 3 4 5 3 4
2) Scrivi quattro f
razioni equival
enti a ciascuna del
l
e seguenti, cal
col
a il numero decimal
e corrispondente
approssimando
ai
centesimi)
e
rappresental
e
sul
l
a
retta
numerica:
3 4 4 2
; ;
;
5 9 14 5
3)Perci
ascuncerchi
ocol
oral
apart
ei
ndi
cat
a
Ci
nquedodi
cesimi
Trequart
i
Duet
erzi
Unmezzo
Undi
cidodi
cesimi
Ci
nquesest
i
4)Scri
vil
efrazi
onichecorri
spondonoaipunt
ii
ndi
catidal
l
efreccenel
l
aseguent
eret
t
anumeri
ca:
5)Di
vi
dendoopport
unament
ei
lsegment
ouni
t
ari
o,i
ndi
vi
duasul
l
aret
t
anumeri
caipunt
icorri
spondent
iaiseguent
i
val
orinumeri
ci:
0,
25;0,
5 ;0,
3;1,
6;0,
1;0,
6;1,
4;1,
2;
3 1 1 1 14 3 2 6 7
; ; ; ; ; ; ; ;
4 4 2 10 10 5 4 5 5
15
6) Completa come nell’esempio.
Frazione
Rettanumerica
Rappresentazione
1
2
Numerodecimale
1 : 2 = 0,
5
__
: = 3
8
: = __
: = 0,
75
__
: = 5
2
: = __
: = 1,
3
__
: = : = __
16
… ..:… ..=
………
… … … ..
7) Risolvere la seguente espressione utilizzando:
a)inumeridecimaliperiodiciapprossimatiallaprimacifra
b)inumeridecimaliperiodiciapprossimatiallasecondacifra
c)trasformandoinumeridecimaliin frazioni.
Confrontareirisultatiottenuti,cosasenepuòdedurre?
_
_
0
,
625
+
4
,
5
⋅
0
,
75
−
0
,
6
÷
0
,
875
+
0
,
75
⋅
2
,
7
−
2
,
3
Verifica comune
(classe2°media e1°superiore)
Approssimazionediunnumeroreale
Dateleespressioni:
1)
[1,3 − 0,5 + 1,16] ⋅ 0,5 + [2,25 − 1,6] ⋅ 0,25.
2)
[(A, ⋅ , − ,( ⋅ !,) ⋅ .] ⋅ (!, − ,A)
Risolviciascunaespressioneintremodidiversi:
a) calcola ilrisultatoutilizzandosolo lanotazione decimaleeapprossimando
inumeriperiodiciallasecondacifradecimalenelprimopassaggio,
neipassaggisuccessivinonfareulterioriapprossimazioni.
b) calcola ilrisultatoutilizzandosololanotazione decimaleapprossimando
inumeriperiodiciallaterzacifradecimalenelprimopassaggio,
nei passaggisuccessivinonfareulterioriapprossimazioni.
c) calcola ilrisultatodopoaveretrasformatociascunnumerodecimale
nellafrazionegeneratricecorrispondente;
d) Diciascunaespressioneconfrontailrisultatoottenutoconilmetodoa) ilrisultato
ottenutoconilmetodob) infineilrisultatoottenutoconilmetodoc)
checosaosservi?Giustificalatuarisposta.
17
RICHIAM ITEORICI
Frazione : ilterminehaoriginedallatinoFractio chederivadafractus (part.pas. difrangere)che
significaspezzare,romperedividereinparti;èopportunorichiamaresempreil significato e
l’etimologia delleparoleusate.
1;2;
3.......} sappiamocheleoperazionidiaddizioneemoltiplicazionesonooperazioni
In N = {0;
b ∈N alloraa+b ∈ N eab ∈ N.
interne: cioèdatiduenumeria,
Ladivisione traduenumerinaturalia eb inveceèinterna solose il dividendo a èmultiplo del
divisore b ( ≠ 0) alloraesiste q taleche a = bq (q sidicequozienteesattooquoto)
Sea= 6 eb=2 allora q= a:b= 6:2 = 3 perché23 = 6
Sea= 7 eb= 2 allora 7 : 2 nonsipuòeseguireperchénon esiste q ∈ N taleche7= 2q
a
Definizione : Sidicefrazione
ilquoziente diduenumerinaturaliaebcon b0
b
(ilnumeratore a èildividendo,
ildenominatoreb èildivisore(≠ 0)
a
6
Sea èmultiplo di b lafrazione èapparente èrappresentaunnumero intero ( = 2 )
b
3
a
=1
b
Sea non èmultiplo di b :
a
lafrazione
è propria se a< b edeseguendoladivisionesiottieneunnumerodecimalecon
b
laparteintera = 0, … … quindi< 1
a
lafrazione
èimpropriasea>b edeseguendoladivisioneottengounnumerodecimalecon
b
parteintera >1
Sea= bottengol’unità
Sea nonèmultiplodib allora q sichiamaquozienteapprossimatocioèq èilpiùgrande
numeronaturalechemoltiplicatoperb risulta a
a:b = q con resto r ossia a = bq +r ossia r= a -bq
NB.E’importantefarcalcolareil resto (almenoognitanto)comedifferenza tra ildividendo eil
prodotto del divisore peril quoziente approssimato enonfarlocalcolare solomentalmente.
Cosìsirinforzal’algoritmodelladivisionecomesottrazionisuccessive,metodo utilizzatoperla
divisionetrapolinomi.
NB Altraosservazioneimportante!!!!(chevieneutilizzataspessoinalgebra)
(èverochelefrazioni godono della proprietà invariantiva : possomoltiplicare o dividere
numeratore e denominatore perunostessonumerodiversodazeroeilquoziente non cambia,
macambia il resto cherisultaanch’essomoltiplicatoodivisoperlostessonumero:
Esempio:
5 10 15
=
=
ma 5:3 daq=1 er=2 ; 10:6 da q=1 mar= 4 15:9 daq= 1 mar= 6
3 6
9
5 10 15
= =………
Cisonoquindiinfini
tefrazioniequivalenti =
3 6
9
18
PossiamochiamareNumero Razionale Assoluto ogniclassedifrazioniequivalentiepossiamo
5
lrappresentantedellaclasse
considerarequellaridottaaiminimitermini,
cioè ,i
3
Qa
L’insiemedituttiinumeri razionali assoluti si indica con Qa . Perché la lettera Q ?
Perché Q è l’iniziale della parola quoziente, cioè di tutti i numeri che si possono scrivere sotto
forma di frazione )
(la parola razionale deriva dal latino ratio – rationis che ha molti significati fra i quali: calcolo o
quoto tra due numeri; il ragioniere è ,non solo una persona che ragiona come tutti noi, ma è colui
che tiene la contabilità di una ditta, cioè fa i calcoli.
La parola razionamento di viveri significa dividere le provviste in parti.
Anche in inglese il termine rapporto è espresso dalla parola ratio come si evince dall’esempio
seguente.
Ecco un quesito tratto da (USA University of North Carolina ,Western Region State Mathematics
Finals 1999)
19
Dalla frazione al numero decimale
Per trasformare una frazione in un numero decimale, basta eseguire la divisione tra numeratore e
denominatore .E’ opportuno far eseguire la divisione tradizionale!!!(almeno di tanto in tanto)
23
46
= 23 : 5 = 4,6 =
5
10
2
= 2 : 3 = 0,66666... = 0, 6
3
4
8
= 4 : 5 = 0,8 =
,
5
10
9
45
37
= 9 : 2 = 4,5 =
,
= 2,46666... ,
2
10
15
21
105
= 1,05 =
,
20
100
7
14
= 1,4 = .
5
10
Avrete osservato che le frazioni il
cui denominatore è composto solo
dai fattori 2 o 5 o da entrambi si
trasformano in numeri decimali
limitati; questi ultimi a loro volta
frazioni
sono equivalenti a
decimali cioè a frazioni con a
denominatore una potenza di 10.
Se il denominatore contiene anche
altri fattori, le frazioni si
trasformano in un numero decimale
periodico semplice o misto.
20
Dalla frazione alla frazione decimale
Iseguenti esempi mostrano come è possibile trasformare una frazione avente a denominatore solo
fattori 2 e 5 in una frazione decimale. Come si vede, è sufficiente moltiplicare il numeratore e il
denominatore con le potenze di 2 e di 5. necessarie a formare una potenza di 10 a denominatore.
4 4⋅2 8
=
=
,
5 5 ⋅ 2 10
9 9 ⋅ 5 45
=
=
,
2 2 ⋅ 5 10
7 7
7 ⋅ 53
875
= 3 = 3 3 = 3 ,
8 2
2 ⋅5
10
Dalla frazione decimale al numero decimale
Esegui le divisioni:
8
105
;
10
100
Dal numero decimale alla frazione decimale
u d
1, 3 = (1+0,3) = 1+
da u d c
2 4, 5 3 = 24 +
3 10 3 10 + 3 13
=
+ =
=
10 10 10
10
10
5
3
2400 50
3
2453
+
=
+
+
=
10 100 100 100 100 100
u d c mm
2, 0 0 3 = 2 +
0
0
3
2000 + 3 2003
+
+
=
=
10 100 1000
1000
1000
21
21
21
21 ⋅ 5 105
= 2 = 2 2 =
.
20 2 ⋅ 5 2 ⋅ 5
100
REGOLA
Dal numero decimale limitato alla frazione generatrice
La frazione generatrice di un numero decimale limitato si determina moltiplicando il numero per la
10 n
frazione n = 1 , dove n indica il numero delle cifre decimali.
10
Esempio: 2,25 =
2,25 100 225
⋅
=
.
1 100 100
La frazione generatrice di un numero decimale finito si ottiene quindi scrivendo a numeratore il
numero senza virgola e a denominatore 1 seguito da tanti zeri quante sono le cifre decimali.
Applichiamo la regola appena descritta per determinare la frazione generatrice di 2,25, si ha:
2,25 =
2,25 =
Riducendo ai minimi termini:
225
.
100
9
.
4
Ricorda che per moltiplicare un numero decimale per una potenza di 10 basta spostare la virgola
verso destra di tanti posti quanti ne indica l’esponente.
Esercizi
Trasforma i seguenti numeri decimali finiti in frazioni:
a) 15,6 b) 0,85 c) 0,028
Soluzioni:a)
78
5
b)
17
20
c)
d) 3,375
7
27
d)
250
8
e) 0,4375
e)
7
.
16
a) 2,53 b) 7,4 c) 15,75 d) 340,9 e) 0,0672 .
Soluzioni: a)
253
37
b)
100
5
c)
63
3409
42
d)
e)
.
4
10
625
22
.
PROBLEM I
Ottenere la frazione generatrice del numero decimale periodico 7, 2 .
Se si moltiplica 7, 2 = 7,222... per 10 si ottiene 72, 2 = 72,222...
La differenza 72, 2 − 7, 2 = 72,222 ... − 7,222 ... genera il numero 65 , privo di parte
decimale, che rappresenta 10 − 1 = 9 volte il periodico assegnato.
7, 2 è pertanto ottenuto dalla frazione
65
.
9
Trasformare il decimale periodico 1,082 in frazione.
Si moltiplica 1,082 = 1,08282... prima per 10 ottenendo 10, 82 = 10,8282... e poi per 1000
ottenendo 1082, 82 = 1082,8282... .
La differenza 1082 , 82 − 10, 82 = 1082 ,8282 ... − 10,8282 ... è il numero intero 1072 , che
rappresenta 1000 − 10 = 990 volte il periodico dato.
1,082 è dunque generato dalla frazione
REGOLA
1072
.
990
Dal numero decimale periodico alla frazione generatrice
La frazione generatrice di un numero decimale periodico si ottiene scrivendo a numeratore la
differenza fra il numero senza virgola e il numero formato dalle cifre che precedono il periodo e a
denominatore tanti 9 quante sono le cifre del periodo seguiti da tanti 0 quante sono le cifre
dell’antiperiodo.
Esercizi:
Trova la frazione generatrice dei seguenti numeri decimali periodici:
a) 0,56 b) 23,3 c) 0, 72 d) 2,06 e) 0,916 .
Soluzioni: a)
17
30
a) 0, 2 b) 5, 23
Soluzioni: a)
b)
70
3
c)
8
31
d)
11
15
11
.
12
e)
c) 0,293 d) 1,97 e) 1,416 .
2
518
22
81
b)
c)
d)
9
99
75
45
e)
17
12
23
Dopo aver stabilito il tipo di decimale, trova la frazione generatrice dei numeri scritti di seguito.
a) 0,015 b) 3,85 c) 7,24
Soluzioni: a)
a) 2,84
7
400
b)
b) 0,134
Soluzioni: a)
c)
326
45
c) 0,875
71
121
7
b)
c)
25
900
40
a) 5,02 b) 0,52
Soluzioni: a)
77
20
d) 93, 81
d)
e) 0,2305 .
10332
11
e)
461
2000
d) 9,255 e) 0,07227 .
d)
833
90
e)
73
1010
c) 0,227 d) 10,4 e) 62,592 .
226
13
5
b)
c)
45
25
22
d)
52
5
e)
7824
125
SINTESI
Un numero decimale illimitato si dice periodico semplice se in esso, subito dopo la virgola, inizia
il periodo, cioè la cifra o il gruppo di cifre che si ripete periodicamente.
Una frazione ridotta ai minimi termini si trasforma in un numero decimale illimitato periodico
semplice se il suo denominatore, scomposto in fattori primi, non contiene i fattori 2 e 5.
Un numero decimale illimitato si dice periodico misto se in esso, fra la virgola ed il periodo, esiste
una cifra o un gruppo di cifre, detto antiperiodo, che non si ripete.
Una frazione ridotta ai minimi termini si trasforma in un numero decimale periodico misto se il suo
denominatore, scomposto in fattori primi, contiene insieme agli altri, i fattori 2 o 5 (o entrambi).
Tabella riassuntiva:
FRAZIONE
Apparente
Ordinaria con denominatore contenente solo
i fattori 2, 5 o entrambi
Ordinaria con denominatore che non contiene
affatto i fattori 2 e 5
Ordinaria con denominatore che contiene oltre i
fattori 2, 5 anche altri fattori
24
TIPO DINUMERO
Numero naturale
Numero decimale limitato
Numero decimale periodico semplice
Numero decimale periodico misto
ESERCIZI
Numeri periodici
Conoscenza deicontenuti
1) Completa:
a) un numero si dice decimale limitato se… … … … … ..
b) un numero si dice periodico semplice se… … … … …
c) un numero si dice periodico misto se… … … … … … ..
2) Riconosci e raggruppa in insiemi diversi le frazioni apparenti, quelle decimali e quelle ordinarie:
11
10
24
8
33
100
9
20
5
3
4
12
1000 6
4
25
233
10
17
33
35
7
50
11
28
15
3) Completa la seguente tabella.
Numero
4,25
0,16
Parte intera
Parte decimale
Periodo
Antiperiodo
Tipo di numero
25
9,21
3,2355
3
.
10
4) Indica la risposta esatta
Il numero 1,24 è un numero
a) decimale limitato
a) decimale illimitato
b) naturale
La frazione
3
è una frazione
20
a) decimale
b) ordinaria
c) riducibile
Il numero 5,8888… . è un numero
a) decimale limitato
b) periodico semplice
c) periodico misto
Il numero 7,23222… è un numero
a) decimale limitato
b) periodico semplice
c) periodico misto
Nel numero periodico misto 9,3547 il periodo è
a) 54
b) 35
c) 47
Se il denominatore di una frazione irriducibile, scomposto in fattori primi, contiene solo fattori
diversi da 2 e da 5, la frazione si trasforma in un numero
a) decimale limitato
b) periodico semplice
c) periodico misto
Se il denominatore di una frazione irriducibile, scomposto in fattori primi, è uguale a 22 × 3 × 5 × 7,
la frazione si trasforma in un numero
a) decimale limitato
b) periodico semplice
c) periodico misto
26
5) Riconosci a quale tipo di numero da origine ciascuna delle seguenti frazioni.
13
: la frazione è… … … … … … … … … … ..e quindi dà origine a … … … … … … … … … … …
10
9
: la frazione è… … … … … … … … … … ..e il suo denominatore, scomposto in fattori primi,
40
contiene solo i fattori… … … … … … … … … … … .. quindi dà origine a … … … … … … … … … …
8
: la frazione è… … … … … … … … … … ..e il suo denominatore, scomposto in fattori primi,
21
contiene solo i fattori… … … … … … … … … … … .. quindi dà origine a … … … … … … … … … …
13
: la frazione è… … … … … … … … … … ..e il suo denominatore, scomposto in fattori primi,
12
contiene solo i fattori… … … … … … … … … … … .. quindi dà origine a … … … … … … … … … …
Applicazione
6) Trasforma le seguenti frazioni nei corrispondenti numeri decimali:
18
9
90
5
21
7
13
5
31
20
7
16
43
8
71
25
9
100
74
1000
47
33
2,74
2,741
7
9
13
11
7) Scrivi i seguenti numeri sottoforma di numeri decimali periodici
1,23232323… .
7,333333… .
56,096565… .
3,844444… …
124,8754754…
30,0455555…
=
=
=
=
=
=
8) Scrivi in ordine crescente i seguenti numeri:
0, 8
0, 81
0,8
0, 85
0,816 0,855 0,85
9) Scrivi in ordine decrescente i seguenti numeri:
2, 5
2, 473
2, 47
2, 74
2,47
10) Inserisci al posto dei puntini a seconda dei casi, il segno di uguaglianza oppure il segno di
maggiore o minore (=; >; <).
4,2… … … … ..4,219
8,9… … … … ..8,809
7,999999… … … 8,1
27
56,1181… ..56,1180
11) Completa la seguente tabella
Frazione
455
1000
53
10
7
100
1321
100
11
1000
113
10
9
10
Divisione
Numero
decimale
12) Trasforma le seguenti frazioni in numeri decimali, stabilendo prima di che numero decimale
si tratta.
7
15
11
25
1
9
9
16
17
8
33
20
14
11
5
27
27
2
13) Metti un denominatore tale che la frazione possa essere trasformato in un numero decimale
limitato.
23
17
37
8
20
123
16
5
14) Metti un denominatore tale che la frazione possa essere trasformato in un numero decimale
illimitato periodico semplice.
12
19
30
51
11
36
44
25
15) Metti un denominatore tale che la frazione possa essere trasformato in un numero decimale
illimitato periodico misto.
10
13
21
4
15
28
38
14
18
ESERCIZI
Rappresentazione di numeri sulla retta numerica
E’ possibile rappresentare i numeri naturali su una semiretta orientata.
Al punto origine O della semiretta si fa corrispondere il numero 0.
Ad un punto A, situato (per convenzione) alla destra di O, si fa corrispondere il numero naturale 1.
La distanza OA sarà l’unità di misura che si userà nel seguito. Infatti gli altri numeri naturali
corrisponderanno a punti che si trovano a distanze da O multiple dell’unità di misura.
Il procedimento puòessere esteso ai numeri interi relativi (utilizzando una retta anziché una
semiretta e rappresentando i numeri < 0 a sinistra del punto preso come origine) e ai numeri
razionali (utilizzando sottomultipli dell’unità di misura).
1) Determina a quale numero corrispondono i punti indicati sulla semiretta, sapendo che il
punto A = 0 e il punto G = 0,2
2) Determina a quale numero corrispondono i punti indicati sulla semiretta, sapendo che il
punto A = 0 e il punto G = 0,1
3) Determina a quale numero corrispondono i punti indicati sulla semiretta, sapendo che il
punto A = 0 e il punto B = 1
4) Determina a quale numero corrispondono i punti indicati sulla semiretta, sapendo che il
punto A = 0 e il punto B = 0,1
29
5) Determina a quale numero corrispondono i punti indicati sulla semiretta, sapendo che il
punto A = 0 e il punto B = 1
6) Rappresenta sulla seguente semiretta i numeri 0,6 1,4
sapendo che il punto A = 0 e il punto B = 1.
7) Rappresenta sulla seguente semiretta i numeri 0,5 2,25
sapendo che il punto A = 0 e il punto B = 1.
30
2/5
12/4
11/10
2,2
36/20
20/8
3,75 35/20
APPROFONDIM ENTO Inumeri periodici
Es n°1 Numero periodico semplice
−
Consideriamo il numero razionale n = 2, 3 , la sua frazione generatrice è
7
.
3
Osserviamola successione di approssimazioni per difetto del
numero:
a0 = 2
a1 = 2,3
a2 = 2,33
a3 = 2,333
a4 = 2,3333
a5 = 2,33333
a6 = 2,333333
Costruiamo un grafico in Excel in cui rappresentiamo an versusn:: possiamo osservare che
all’aumentare dei termini della successione, l’ordinata dei punti non cresce visibilmente ma tende a
7
raggiungere un valore costante che rappresenta
.
3
Es n°2 Numero periodico misto
−
Consideriamo il numero razionale n = 2,8 3 : la sua frazione generatrice è
17 283 − 28 255
=
.
=
6
90
90
Consideriamo la
successione an
a0 = 2
a1 = 2,8
a2 = 2,83
a3= 2,833
a4= 2,8333
a5= 2,83333
a6 = 2,833333
Possiamo osservare come prima che all’aumentare dei termini della successione, l’ordinata dei
17
.
punti non cresce visibilmente ma tende a raggiungere un valore costante che rappresenta
6
31
DAINUM ERIPERIODICIAINUM ERIIRRAZIONALI
Laboratorio n°1
Alle scuole medie si puòproporre di usare la piegatura del foglio A4 per scoprire oggetti di uso
quotidiano che hanno misure espresse da numeri irrazionali !!
1)Si chiede di piegare il foglio costruendo un quadrato di lato 1u ,la diagonale del quadrato
sarà 2 u.
2)Si sovrappone la diagonale ottenuta con il lato maggiore del foglio che risulta essere quindi
3)Si applica il teorema di Pitagora alla metà del foglio ottenendo che la diagonale misura
32
3.
2 u.
Laboratorio n°2
Costruire un quadrato di area doppia di un quadrato unitario
•
Costruire i quadrati di lato l = 1,2,3,4... (vedi file Geogebra)
Come si può osservare dalla figura , se raddoppio il lato ottengo un quadrato di area quattro volte
quella iniziale, se lo triplico ottengo 9 volte quella iniziale e cosìvia … non ottengo mai un’ area
doppia.
Peròpossiamo osservare che il lato del quadrato deve essere compreso tra 1 e 2 ossia 1 < l <2
•
Tracciamo ora la diagonale del quadrato unitario e costruiamo il quadrato che ha per lato la
diagonale stessa
Finalmente abbiamo costruito il quadrato di area doppia !Infatti il Teorema di Pitagora ci assicura
che AC2 =
(l
2
+l2
) = 2⋅l
2
Quindi se l =1 allora AC =
2
2
33
Il rapporto tra il lato e la diagonale del quadrato èun numero irrazionale
TEOREM A
2∉ Q
(
2 non appartiene a Q )
Dim.: Supponiamo per assurdo che
2=
p
con p e q primi fra loro e quindi non entrambi pari.
q
Si puòallora scrivere, in virtùdel secondo principio di equivalenza per le equazioni:
2q = p .
Essendo un’uguaglianza tra numeri positivi, si puòelevare al quadrato entrambi i membri:
( 2q )
2
= p 2 → 2q 2 = p 2 .
Quest’ ultima uguaglianza è assurda perché il primo membro contiene un numero dispari di fattori
2, mentre il secondo o non ne contiene o ne contiene un numero pari.
Questa dimostrazione sottintende il teorema di unicità della scomposizione in fattori primi1
dimostrato già nel libro VIIIdegli Elementi di Euclide.
1
Si veda anche: J. P. Delahaye
Stupefacenti numeri primi
34
Ghisetti e Corvi.
Se utilizziamo Derive per approssimare tale numero con 9 cifre decimali otteniamo:
2 1.414213562.
Con piùdi 100 cifre decimali otteniamo:
1.414213562373095048801688724209698078569671875376948073176679737990732478462107
0388503875343276415727350138462309122970249248
Se anche chiedessimo piùcifre ci accorgeremmo di non riuscire a trovare alcuna periodicità.
Possiamo comunque costruire la successione:
a0 = 1
a1 = 1,4
a2 = 1,41
a3 = 1,414
a4 = 1,4142
a5 = 1,41421
a6 = 1,414213..
Essa è una successione crescente che approssima per difetto 2 senza mai raggiungerlo… … .
Possiamo osservare che, all’aumentare dei termini della successione, l’ordinata dei punti non cresce
visibilmentema tende a raggiungere un valore costante che rappresenta 2 .
35
Laboratorio n°3
Rappresentare sulla scala dei numeri alcuni numeri irrazionali con metodo grafico o meccanico2.
Rappresentazione di tre numeri irrazionali
sulla scala dei numeri.
π nasce dalla rotazione completa senza
scivolamento di un cerchio di diametro
unitario; gli altri numeri hanno origine
dall’applicazione del teorema di Pitagora a
triangoli rettangoli aventi la misura dei
cateti espressa da numeri naturali.
LABORATORIO N°4
“Chiocciola dei numeri”
Si propone di riprodurre questa
figura su di un foglio da disegno ;
poi di riportare, con il compasso,
su di una semiretta orientata, i
segmenti
che
rappresentano
numeri irrazionali.
Ogni ipotenusa dei triangoli
rettangoli (AC, AE, AF, AG, AH,
AI, AJ… ) rappresenta un numero
intero oppure irrazionale che
Geogebra approssima alla seconda
cifra decimale.
2
Si veda la concoide di Nicomede, curva meccani
ca.
36
UNA DEFINIZIONE
Una terna ordinata di numeri naturali diversi da zero ( x, y, z ) , con x < y , è detta pitagorica se:
z2 = x2 + y2 .
Itre numeri naturali sono la misura rispettivamente dei cateti e dell’ipotenusa di un triangolo
rettangolo.
LABORATORIO N°5 Caccia alle terne pitagoriche
Figura 3
Si chiede di disegnare su di un foglio a quadretti tanti triangoli rettangoli la cui misura dei cateti
sia un numero naturale.
3
a)
Mediante un compasso oppure con calcolo diretto si identificano le ipotenuse di misura
intera, scoprendo cosìle piùcomuni terne pitagoriche.
b)
Se si lavora con piccoli quadretti si puòscoprire l’esistenza di classi di terne tra di loro
proporzionali. Es.: (3a,4a,5a ) , a ∈ N .
c)
Si puòapprofondire costruendo per ogni classe di cui sopra delle “terne pitagoriche”di
3 4 5
numeri razionali. Es.: , , .
7 7 7
d)
Si puòampliare il discorso dicendo che il problema delle terne pitagoriche è stato
completamente risolto da Fermat3.
L. Berzolari, G. Vizianti, D. Gigli Enciclopedia delle matematiche elementari
37
Pagine
LABORATORIO N°6
«… i matematici sono persone sensibili… »
Il prof. Phumble affermava di aver dimostrato il seguente teorema: «Non esistono due differenti
terne pitagoriche che abbiano lo stesso terzo numero».
In altri termini: non esistono due terne pitagoriche tali che:
2
2
2
2
x1 + y1 = z 2 e x 2 + y 2 = z 2 ,
con x1 ≠ x 2 e y1 ≠ y 2 .
Pierino ha messo da parte il videogioco preferito e, con l’aiuto del fedele
computer e di DERIVE, ha prodotto l’elenco di terne pitagoriche della pagina
seguente.
Il prof. Phumble si è arrabbiato moltissimo!
a)
Verifica con l’aiuto della calcolatrice che queste terne sono effettivamente pitagoriche.
b)
Scopri con l’aiuto del tuo insegnante alcune particolarità delle terne di questo elenco:
Pierino è molto bravo al computer, ma ha commesso alcuni piccoli errori nella
programmazione.
c)
Spiega perché il prof. Phumble si è arrabbiato moltissimo.
38
Figura 4:Le terne pitagoriche di Pierino4.
4
La soluzione si puòtrovare osservando attentamente la copertina di questo opuscolo.
39
Problema :
Le squadre A, B, C di un torneo di calcio hanno giocato 13 partite con i seguenti risultati:
VITTORIA
PAREGGIO
SCONFITTA
risultato
squadra
In casa
Fuori casa
In casa
Fuori casa
In casa
Fuori casa
A
3
5
1
1
1
2
B
-
5
1
7
-
-
C
1
3
6
1
2
-
Tenendo conto che nel campionato di calcio italiano si assegnano ad ogni squadra e per ogni
partita giocata 3 punti in caso di vittoria, 1 punto in caso di pareggio e 0 punti in caso di
sconfitta, mentre nel campionato inglese il punteggio si ricava dalla seguente tabella
VITTORIA
PAREGGIO
SCONFITTA
In casa
0
-1
-2
Fuori casa
+2
+1
0
Calcola i punteggi e forma le graduatorie delle tre squadre in base ai due metodi considerati.
40
NUM ERIREALIE OPERAZIONI
L’ insieme dei numeri reali è ordinato . Un numero reale relativo è un numero dotato di segno. I
segni
sono +
e
–,
il
modulo
o
valore
assoluto
del
numero
è
così definito
a = a se a ≥ 0 oppure a = − a se a < 0 .
a∈R
Segno
Modulo
+3
+
+3 3
−3
–
+3 3
5
4
–
−
− 20
–
+
Rappresentazione sulla scala numerica
5 5
4 4
+ 20 ≡ 20
41
CONFRONTO TRA DUE NUM ERIREALI RELATIVI
Due numeri relativi si dicono:
a) Concordi, quando hanno lo stesso segno (+3, +7)
b) Discordi se hanno segno diverso (-3, +7).
c) Uguali, quando hanno lo stesso segno e lo stesso modulo (-5, -5).
d) Opposti, quando hanno lo stesso modulo e segno diverso (-9, +9).
e) Se accade che a < b , l’immagine di a giace alla sinistra dell’immagine di b:
7 8
7
8
7 8
7 < 3 , − 7 > −3 ,
1 > −731 …
< , − >− , − < ,
6 7
6
7
6 7
DEDUZIONE DELLE REGOLE PER LA SOM M A ALGEBRICA .
+ 2 + 3 = +5
− 4 + 3 = −1
+ 6 − 4 = +2
+ 3 − 4 = −1
− 2 − 4 = −6
42
Aggiungere+3 al numero+2 equivalea traslareversodestra ditreunitàl’immaginedi+2.
Aggiungere+3 ad un numeroequivalea traslareversodestra ditreunitàl’immagineditale
numero.
Sottrarre4da +6equivalea traslareversosinistra diquattrounitàl’immaginedi+6.
Sottrarre4da un numeroequivalea traslareversosinistra diquat
trounitàl’immagineditale
numero.
1) La somma di due numeri concordi èun numero concorde con essi e che ha per modulo la
somma dei moduli .
Esempio a)
(+4) + (+6) = + 4 + 6 = + 10.
Esempio b) (–2) + (–7) = –2 –7 = –9.
2) La somma di due numeri discordi è un numero che ha il segno del numero con modulo
maggiore e per modulo la differenza dei moduli.
Esempio: (+4) + (–2) = 4 –2 = 2
SOTTRAZIONE TRA NUM ERIRELATIVIin Z
Per sottrarre due numeri relativi si somma al primo l’opposto del secondo.
Esempio a: (+4) –(–3) =
4 +(+3) = 4+3 = 7.
Esempio b: (+5) –(+2) = 5 + (–2) = 3
43
ESERCIZI
1) Scrivi i numeri dell'insieme Z (numeri relativi)che hanno valore assoluto minore di 4.
2) Scrivi i numeri dell'insieme Z che hanno valore assoluto compreso tra 6 e 9.
3) Scrivi tre coppie di numeri interi relativi concordi e tre coppie di numeri razionali
relativi concordi con le seguenti caratteristiche:
a) i numeri minori di ogni coppia hanno valore assoluto minore di 8;
b) i numeri maggiori di ogni coppia hanno valore assoluto compreso tra 10 e 30.
4) Scrivi tre coppie di numeri interi relativi concordi e tre coppie di numeri razionali
relativi concordi con le seguenti caratteristiche:
a) i numeri minori di ogni coppia hanno valore assoluto compreso tra 1 e 14;
b) i numeri maggiori di ogni coppia hanno valore assoluto compreso tra 10 e 25.
5) Scrivi tre coppie di numeri interi relativi opposti e tre coppie di numeri razionali
relativi opposti con le seguenti caratteristiche:
a) i numeri minori di ogni coppia hanno valore assoluto minore di 8;
b) i numeri maggiori di ogni coppia hanno valore assoluto maggiore di 6 e minore di 12
6)
7)
8)
44
9)
10)
Completa le seguenti frasi con “è”oppure con “non è”oppure con “puòessere”.
La somma di due numeri relativi positivi … … … … … … … un numero positivo.
La somma di due numeri relativi negativi … … … … … … … un numero positivo.
La somma di due numeri relativi concordi(numeri con lo stesso segno)… … … … … … …
un numero positivo.
La somma di due numeri relativi discordi(numeri con segni diversi) … … … … … … … un
numero positivo.
La somma di due numeri relativi opposti … … … … … … … un numero
positivo.
11)
Alle otto di mattina Gianni misura la temperatura dentro un contenitore in cui avviene
una reazione chimica; la temperatura è di +3°C. Alle nove la temperatura è scesa di 5°,
alle dieci la temperatura è risalita di 7°, alle undici è ridiscesa di 4°C.
Quale temperatura si puòleggere alle undici?
12)
Completa il quadrato magico in modo che la
somma algebrica in ogni riga, in ogni colonna e
sulle diagonali sia la stessa.
45
13)
1.
2.
3.
4.
5.
6.
7.
Vero o falso?
Due numeri relativi sono concordi se hanno segni opposti
Due numeri relativi si dicono opposti se hanno segni diversi
Tra due numeri relativi il maggiore è sempre quello con il modulo maggiore.
Nell’addizione di due numeri si sommano sempre i moduli
Nella sottrazione di due numeri negativi si sottraggono i moduli
Il segno di una somma di numeri relativi è uguale al segno del maggiore
Se la somma di due numeri relativi è nulla allora i due numeri sono opposti.
46
14)
Compila la tabella sottostante aggiungendo i simboli “∈ ”e “∉ ”.
47
16) Risolvi le seguenti addizioni fra i numeri relativi.
a) (-1/3) + (-4/5) = ..............................
b) (+2/5) + (- 7/8) = .............................
c) (-6/7) + (+1) = ...............................
d) (-4/9) + (+5/12) = ...........................
17)
Risolvi le seguenti addizioni fra numeri decimali relativi.
a) (-0,8) + (+4,1) = ..............
b) (+2,3) + (-0,4) = ...............
c) (-8) + (-6,7) = ...................
18)
Risolvi le seguenti addizioni con piùaddendi.
a) (+1/2) + (-2/5) + (-3/4) = ............................
b) (-7/8) + (-3/4) + (+9/2) + (-1) = ....................
19) Ordina sulla retta dei numeri i seguenti valori.
a.
-3;
5;
-1/3;
-5/4;
+3/8;
9/8;
-1.
b.
+4;
-7;
-5/3;
+9/4;
-7/2;
6/7;
-5
c.
-2;
1/3;
-5/7;
-9/4;
+2/11;
-81/8;
-1/2.
d.
-3;
2;
-7/3;
-13/4;
+7/4;
13/8;
-1/5.
20) Esegui le seguenti somme algebriche
A) +
4 9
+
5 15
D) +
3 5
1 4
−
+ − +1
8 20 15 5
B) − 1 +
E)
9
5
C) −
3 5
1
− +
4 12 15
3 5 1 4 1
+ − + − + 1 − − 1
8 20 15 5 10 48
LA M OLTIPLICAZIONE TRA NUM ERIRELATIVI
Esempio: (+3) ⋅ 5 = (+3) + (+3) + (+3) + (+3) + (+3) = +15
Esempio : (-3) ⋅ 5 = (-3) + (-3) + (-3) + (-3) + (-3) = -15
Ma perché (-3) ⋅(-5) = +15?
Per la legge di Hankel5 (principio di permanenza delle regole di calcolo), se in matematica si vuole
generalizzare un concetto al di là della sua originaria definizione, bisogna scegliere, tra tutti i modi
possibili, quello che permette di conservare immutate le regole di calcolo nel più esteso numero di
casi.
Si ha quindi, che per la proprietà di annullamento del prodotto:
[(-3) + (+3)]⋅(-5) = 0 ⋅ (-5) = 0
e per la proprietà distributiva:
[(-3) + (+3)]⋅(-5) = [(-3) ⋅ (-5)]+ [(+3) ⋅ (-5)]= (-3) ⋅ (-5) + (-15)
dalle due proprietà segue che (-3) ⋅ (-5) deve essere l’opposto di -15 cioè +15
Si può allora costruire la regola dei segni attraverso la tabella:
REGOLA DEISEGNI
×
+
-
+
+
-
-
-
+
Esiste anche una simpatica regola applicabile a diversi contesti,
+ ⋅ + = + L’amico di un mio amico è un amico
+ ⋅ - = - L’amico di un mio nemico è un mio nemico
- ⋅ + = - Il nemico di un mio amico è un mio nemico
- ⋅ - = + Il nemico di un mio nemico è un mio amico
Due numeri relativi si dicono reciproci o inversi se il loro prodotto è uguale a +1
1
Esempi: il reciproco di + 5 è +
5
5
Hermann Hankel (1839-73), creatore di una teoria logica sui razionali, critico feroce della teoria degli irrazionali!
49
LA DIVISIONE TRA NUM ERIRELATIVI
ESERCIZI:
1) Vero o falso?
Il risultato di (+5) × (+2) è uguale a quello di (+5) + (+5)
Il risultato di (-3) × (+4) è uguale a quello di (-3) + (-3) + (-3) + (-3)
Il prodotto di due numeri concordi è un numero negativo
Il prodotto di due numeri discordi è un numero positivo
positivo
2) Sbarra la casella con la risposta corretta
Il prodotto di due numeri concordi è:
Il prodotto di due numeri discordi è:
Il prodotto di due numeri negativi è:
Il prodotto di due numeri opposti è:
Il prodotto di due numeri uguali è:
V
F
negativo
3) Rispondi alle seguenti domande:
a) Il prodotto di piùnumeri relativi di cui due negativi è positivo?… … … … … … … … ...
b) Se in una moltiplicazione di piùfattori tre sono negativi, il prodotto è negativo?… … .
c) Da quale segno è preceduto il prodotto di quattro numeri negativi?… … … … … … … .
d) Se i fattori negativi di una moltiplicazione sono in numero dispari, il prodotto è
negativo o positivo?… … … … … … … … … … … … … … … … … … … … … … … … … …
e) E se sono in numero pari?… … … … … … … … … … … … … … … … … … … … … … … .
f) Il valore assoluto del prodotto di due numeri relativi puòessere minore di quello di
entrambi i numeri?… … … … … … … … … … … … … … … … … … … … … … … … … …
g) Il prodotto di due numeri negativi è maggiore di entrambi?… … … … … … … … … …
h) Il prodotto di due numeri discordi, diversi da +1 e –1, è minore di entrambi?… … … .
i) Il prodotto di due numeri uguali è positivo?… … … … … … … … … … … … … … … … .
j) E di due numeri opposti?… … … … … … … … … … … … … … … … … … … … … … … …
4) Dopo aver completato la tabella dei segni, rispondi alle domande:
:
+
-
+
a) Il quoziente di due numeri concordi è positivo?… … … … … … … … … … … … … … … … …
b) E il quoziente di due numeri discordi?… … … … … … … … … … … … … … … … … … … … …
50
5) Vero o falso?
Il quoziente di due numeri negativi è maggiore di entrambi
Il quoziente di due numeri positivi, diversi da +1, è minore di entrambi
Il quoziente di due numeri discordi, con valore assoluto diverso da 1,
è sempre maggiore di entrambi
Il quoziente di due numeri discordi, con valore assoluto diverso da 1,
è sempre minore di almeno uno di essi
6) Sbarra la casella con la risposta corretta
Il quoziente di due numeri uguali è
Il quoziente di due numeri opposti è:
Il quoziente di un numero relativo e +1 è uguale:
Il quoziente di un numero relativo e -1 è uguale:
V
F
+1
-1
+1
-1
al numero al suo opposto
al numero al suo opposto
7)Esegui le seguenti moltiplicazioni:
+5 × (+9) =… … … … … ..
-3 × (+7) =… … … … … ..
+4 × (-6) =… … … … … ..
-2 × (-8) =… … … … … ..
+9× -(10) =… … … … … ..
-7 × (-5) =… … … … … ..
1
− 6 × − = ....................
3
5 2
7 4
− × + = ................
+ × − = ................
4 5
2 21 1 1 2
-2 × (+7) × (-3) =… … … … … … .
+ × − × + = ...........................
3 2 3
8) Trova il valore di x:
+ 16 ⋅ ( x) = −16 − 25 ⋅ ( x) = 0
+ 8 ⋅ ( x) = +32
− 7 ⋅ ( x) = −35
5
1
1
2
4
3
1
x ⋅
+ = +
x ⋅
− = +
x ⋅ − = +2
x ⋅
− = −
3
3
4
3
9
4
8
9) Completa la seguente tabella:
a
b
-3
+5
+6
-2
a⋅b
a ⋅ ( −b )
− a ⋅ (−b)
51
− a ⋅ ( + b)
5
6
9
5
2
−
+3
3
-
2
10)Dati i numeri - e +10, calcola:
5
a) il loro prodotto
b) il prodotto dei loro opposti
c) il prodotto dei loro inversi
d) il prodotto del primo per l’inverso del secondo e)il prodotto dell’inverso del primo
per l’opposto del secondo
11)Calcola il valore delle seguenti espressioni:
{− 20 + 4 ⋅ [(− 13 + 15 − 3) ⋅ (− 5) − 6]} − (− 8) ⋅ (+ 3)
1 7 9 5 3 2 1 5 4 − + ⋅ − + ⋅ − − − − ⋅ 1 − 12 4 20 2 14 7 3 12 3 12)Trasforma le seguenti indicazioni in un’espressione e calcolane il valore:
a. Moltiplica la differenza di –6 e + 4 per l’inverso di +10
7
1
b. Sottrai dal prodotto di + e –2 il prodotto di –3 e +
4
4
1
2
c. Moltiplica la somma di − e + per la differenza di +5 e –4
3
9
2
7
d. Moltiplica per +5 la somma di + e −
e dal risultato sottrai il prodotto di
5
15
4
3
+ e−
9
2
13)Esegui le seguenti divisioni:
-39 : (+13) = … … …
+24 : (-3) =… … … …
-72 : (-12) =… … … … .
+36 : (-6) =… … … ..
+93 : (+ 3) =… … … ...
+49 : (-7) = … … … … .
+
21 7 : − = ..................
4 3
-28 : (-4) : (-1) =… … … … … … .
−
15 5 34 17 : − = ................
: + = ................
+
8 2
15 30 5 3 5
− : − : − = ...........................
4 8 6
52
Trova il valore di x:
− 1 : ( x) = −
2
7
3
3
− : ( x) = +
8
2
4
1
: ( x) = +
5
3
− 6 : ( x) = +12
−
1
a : (+ )
b
1
: (−b)
a
14)Completa la seguente tabella:
a
-3
+1
-
1
2
b
a:b
a : (−b)
+6
5
4
1
8
+
2
15)Dati i numeri + e -6, calcola:
3
a) il loro quoziente b) il quoziente dei loro opposti
secondo
c) il quoziente tra il primo e l’inverso del
d) il quoziente tra il secondo e l’opposto del primo e) il quoziente tra il secondo e
l’inverso del primo.
16)Calcola il valore delle seguenti espressioni:
{[− 10 − (45 + 17 − 30) : (− 4) − 16] ⋅ (− 3) − 12} : (− 10 + 3)
1 5 1 4 3 1 5 5 3
2 − − : + ⋅ 1 + − : − − − 1 − 2 3 15 5 4 2 6 4 5
18)Trasforma le seguenti indicazioni in un’espressione e calcolane il valore
1
5
e poi aggiungi –1
a) Moltiplica per –5 il quoto di + e 9
6
8
1
b) Al quoziente di –4 e + sottrai la somma –3 e 9
2
7
1
3
c) Dividi la somma di + e - per la differenza di +1 e +
6
3
8
2
3
5
d) Sottrai - dal quoziente di - e + 6 e poi moltiplica il risultato per +
5
5
3
53
POTENZE DEINUM ERIRELATIVI
Il termine “potenza” assume significato matematico nel 1550 e deriva dal latino “potentia”, da
potere. La potenza si definisce come la qualità di esercitareun potere.
In particolare in matematica le potenze possono aiutare ad esprimere in forma abbreviata numeri
molto grandi o molto piccoli.
Per esempio:
- la distanza Terra-Sole: 150.000.000 km
puòessere scritto:
15 ⋅ 10 7 km
- la distanza Terra- Alpha Centauri: 40.000.000.000.000 km
puòessere scritto:
4 ⋅ 1013 km
- il diametro dell’atomo di H (idrogeno): 0,0000000012 mm
Il vantaggio di usare le potenze a base 10 è innegabile.
Sappiamo che: - il prodotto di un numero a per un numero b si scrive: ab;
- il prodotto di tre fattori a,
b,
c si scrive: abc.
Se il fattore è sempre lo stesso, come quando dobbiamo calcolare l’area di un quadrato, invece di
scrivere aa si scrive a2 e leggiamo “a al quadrato”,oppure quando dobbiamo calcolare il volume
di un cubo invece di scrivere aaa si scrive a3, che leggiamo “a al cubo”.
Per abbreviare la scrittura di un prodotto di più fattori tutti uguali(a), è sufficiente contarli e
scrivere il numero trovato n ad esponente a. Cosìl’abbreviazione di un prodotto di n fattori uguali
ad a, è una potenza di a indicata an: dove n è l’esponente di a, e si legge “a alla n” o “a elevato
all’ennesima potenza”.
Esponente
n
a =aaaaa… a
Base
Per calcolare la potenza di un numero relativo:
a) prima si scrive il segno del risultato;
b) poi si eleva a potenza il valore assoluto della base.
Ecco alcuni esempi:
2
1. (− 2 ) = (− 2 ) ⋅ (− 2 ) = +4
2
2. (+ 2 ) = (+ 2 ) ⋅ (+ 2 ) = +4
2
1
1
1 1
3. − = − ⋅ − = +
4
2
2 2
3
4. (− 2 ) = (− 2 ) ⋅ (− 2 ) ⋅ (− 2 ) = −8
3
5. (+ 2 ) = (+ 2 ) ⋅ (+ 2 ) ⋅ (+ 2 ) = +8
54
Dall’analisi degli esempi si possono fare alcune considerazioni:
Ilsegno della potenza èsempre“+”,
indipendentemente dalla base,la quale
puòessere positiva o negativa.
PARI
Quando l’ESPONENTE è
Ilsegnodellapotenzaè“+”,
se la base è positiva.
DISPARI
Ilsegnodellapotenzaè“-”,
se la base è negativa.
Dato un numero a ≠ 0 la scrittura an ha significato per qualunque valore di n.
In particolare:
a) se n=1, a1 coincidecon a,ovvero il risultato è sempre uguale alla base. L’esponente 1 può
1
2
2
essere sottointeso. Es.: (− 3) = −3 , = .
3
3
b) se n = 0, a0coincidecon 1,ovvero il risultato è sempre uguale a 1 ;
c) se a = 0 allora l’espressione 00 non ha significato, rappresenta cioè una forma
1
0
5
0
0
indeterminata. Es.: (− 8) = 1 , − = 1 , (+ 3) = 1 .
9
TIPO DIPROPRIETA’
Moltiplicazione di potenze
con uguale base
Divisione di potenze
con uguale base
PROPRIETA’DELLE POTENZE
ESEM PIO
ENUNCIATO
Il prodot
t
odidueopi
ùpot
enzeavent
iper
basela st
essa base,èuna pot
enza cheha
2
3
5
(+ 6) ⋅ (+ 6) = (+ 6)
perbasela st
essa baseeper
esponent
ela somma degliesponent
i
.
Il quoziente di due potenze aventi
per base la stessa base, è una potenza
(− 8)7 : (− 8)5 = (− 8)2
che ha per base la stessa base e per
esponente la differenza degli esponenti.
4
Potenza di una potenza
8
3 2 3
− = − 8
8 La potenza di una potenza è una
potenza avente per base la stessa base
e per esponente il prodotto degli esponenti.
M oltiplicazione di potenze
con uguale esponente
(+ 2)4 ⋅ (− 5)4 = (− 10)
Divisione di potenze
con uguale esponente
(+ 18)5 ÷ (− 6)5 = (+ 3)5
Il prodotto di due o piùpotenze aventi
per esponente lo stesso esponente è una
potenza che ha per base il prodotto delle
basi e per esponente lo stesso esponente.
Il quoziente di due potenze aventi per
esponente lo stesso esponente è una
potenza che ha per base il quoziente delle
basi e per esponente lo stesso esponente.
4
55
SINTESI
ar=an+m
an:am=an-m
con nm
(an)m=anm
anbn=(ab)n
an:bn=(a:b)n
POTENZE CON ESPONENTE NEGATIVO
Perspiegare come si genera l’esponente negativo nelle potenze,si considera una divisione tra
potenze che hanno base uguale ed esponente diverso.
(+ 3)5 : (+ 3)8 = (+ 3)+5−8 = (+ 3)−3
Dato che l’esponente della prima potenza è minore di quello della seconda potenza (58),
otteniamo una potenza con esponente negativo (-3).
1)Applicando la IIproprietàdelle potenze
an:am=an-m
(+3)-3
(+3)5: (+3)8= si puòrisolvere
in due modi:
2)Pervia elementare,scrivendolo sotto forma di frazione
Eguagliando i risultati,si ha che:
(+ 3)
−3
=
1
(+ 3)3
oppure
(+ 3)
−3
1
=
3
3
Quindi:
“Una potenza con esponente negativo è una potenza che ha per base l’inverso della base e per
esponente l’opposto dell’esponente”
In generale:
a −n =
1
an
oppure a
−n
1
=
a
n
con a 0.
Sequenzaoperativa:
1) Invertire la base (a0);
2) Cambiare segno all’esponente (n).
Alcuni esempi:
1
1
a −3 = 3
….
a −2 = 2
a
a
Perchéuna potenza elevata a zero ha sempre come risultato 1?
Possiamo interpretarla anche così:
Il prodotto di due potenze che hanno la stessa base,ma opposti esponenti,si ottiene moltiplicando la
potenza stessa peril suo inverso,si vede che il risultato è1.
2 3 ⋅ 2 −3 = 2 3 ⋅
1
1
= 8⋅ =1
3
8
2
quindi
20 =1.
56
ESERCIZI SULLE Potenzedinumerirelati
vi
1) Il Professor M athnon ha completato tutte le caselle delle tabelle ed ha commesso
alcuni errori aiutalo tu:
ESPONENTE
2
+8
0
0
+64
+20
B
A
S
E
1
2
-5
1
-400
0
-8000
1
1
0
-1
1
-4
+16
-4
-4
-64
-1
-1
-1
-1
-1
-
1
3
-0,
2
+
1
9
0,
04
1
-0,
2
-0,
2
-0,
008
2)Completando la tabella il ProfessorM athègiunto alle seguenti conclusioni:
Quando la base èpositiva e l’esponente pari,la potenza è……………………….
Quando la base èpositiva e l’esponente èdispari,la potenza è………………….
Quando la base ènegativa e l’esponente pari,la potenza è………………………
Quando la base ènegativa e l’esponente èdispari,la potenza è………………….
Quando l’esponente èzero,la potenza èsempre……………………………….
.
Quando l’esponente èuno,la potenza è……………………………………….
3) A questo punto il ProfessorM athsi èdivertito a creare alcuni semplici esercizi,ma è
sempre molto distratto e omette o sbaglia qualcosa:
4
(-3)=…….
1
=…….
2
(-6)2=…….
3
.
=….
4
3
00=………
3
0
2
(-11)=….
.
.
5
=……
7
57
01=……
82
=……
9
-72=……
+132=……
2
-….
=121
(-14)…=196
43 = 64
(-3)…=+81
esercizisul
le Potenzeconesponenteinteronegati
vo
1) Il Prof.M ath,in gioventù,utilizzando le proprietà delle potenze,riuscìa determinare il
7 ⋅ 10 −23 g,e quella dell’elettrone,che è
rapporto tra la massa di un protone,che èuguale a 1,
uguale a 9,
1 ⋅ 10 −28 gr.Purtroppo ora èun po’anziano e non ricorda più il dato che aveva
trovato,prova ad aiutarlo.
2) Ora che gli fa fatto ricordare il meccanismo risolutivo,il Prof.si è divertito a esprimere
altre misure in forma standard,usando le potenze con esponente negativo.Alcune di quelle
risolte
sono le seguenti:
Il diametro del batterio Brucella melitensis: 0,
00003 m:………………………….
.
Il diametro di un globulo rosso: 0,
000007m:……………………………
Il diametro di un cloroplasto:0,
005 mm:……………………………….
.
3) M r M ath decide di compilare una tabella, in cui annotare i passaggi fondamentali da
effettuare nel calcolo delle potenze con esponente negativo,peressere sicuro di ricordarli
anche in futuro,senza commettere grossolani errori.
POTENZA
con
esponente
negativo
Inverso Opposto Potenzacon Valore
della
della dell’espo- esponente
potenza
positivo
nente.
base
1
5
-2
(5)
+2
(-9)-2
(22)-1
(-4)-3
1
− 4
2
3
−3
−5
7
− 6
−1
58
1
5
2
1
25
ESPRESSIONI CON LE POTENZE
Perfinire M rM athdecide di mettere insieme le conoscenze che ha sulle potenze e di inventare
delle espressioni, nella soluzione ha commesso alcuni errori, prova ad individuarli ed a
correggerli.
1)
(− 3) : (− 3) ⋅ (− 3) : [(− 3)
5
2
0
3
−2
5
−6
−2
] ⋅ [(− 3) ]
= (− 3) : (− 3) ⋅ (− 3) ⋅ (− 3)
= (− 3) ⋅ (− 3)
−1 −2 0
−4
−
⋅ (− 3)2 −
=
=
=
1
= (− 3) = −3
25
2)
3
− − 5
−2
=
25
9
= 25 ⋅ − = −9
25
25 −
9
3)
{[(−2)
] ⋅2 +[5 : (5 :5 )]}
= {[−2] ⋅ 2 +[5 : 5]} =
−2
: (−2)
0
0
2 2
2
0
2
3
2
−2
=
−2
−2
= {1+5} =
2
= { 6} =
= 36
PROBLEM I
1) Platone,filosofo dell’Antica Grecia,morìnel 347 a.
C..
Sapendo che visse 80 anni quando è
nato?
2) Nel triangolo in figura,i “+” e i “-“ devono essere disposti in modo da soddisfare la solita
regola dei segni ,ma il matematico che l’ha realizzato ha commesso alcuni errori.Individuali,
correggili e completa l’ultima riga in modo tale che il numero dei “+”sia 15 e il numero dei “-“
sia 13,
in modo che compaiano 15 segni + e 13 segni -.
-+ + + + -+ - + - - - +
+ - +
- 59
+
3) Il ragno Ernesto perfinire di tessere la sua ragnatela deve arrampicarsi su un muro alto 12
metri.Poichéèun po’anziano,il suo lavoro procede a rilento.Avanza di 2 metri ogni mezz’ora
e,sempre ogni mezz’ora fa una sosta di trenta minuti scivolando indietro di 1 metro.A che ora
raggiunge la sommitàdel muro,considerato che ha iniziato il suo viaggio alle 5 del mattino?
4) M arco gioca a carte con tre amici.Nella prima partita vince 20 punti con il primo giocatore,
perde 50 con il secondo,vince 170 punti con il terzo.Nella seconda partita vince 40 punti con
ogni giocatore.Nella terza vince 5 punti con il primo,pareggia con il secondo e vince 43 punti
con il terzo.Qual èla sua situazione finale?
5) Alle 00:00 del 2000 l’orologio di un computerimpazzisce.Va avanti di 7 ore e indietro di 2 ore.
Che orario segna alla fine?
6) Uno sciatore parte perla sua discesa da quota 1650m,scende all’inizio di 200m,poi risale di 50
m perrecuperare la racchetta che ha perso durante il tragitto.Finalmente riparte e scende di
165m,arriva ad un rifugio che si trova a quota 1156m,dove decide di sostare.Quanti metri ha
percorso?Piùdi 700 o meno?
7) Calcola quanti anni sono passati dall’introduzione della numerazione egiziana (4000 a.
C.
)a
quella romana (750 a.
C).
60
Geometria piana
Competenze
Equivalenza Confrontare e
analizzare figure
difigure
geometriche e
piane
calcolarne l’area
M isuradella
Utilizzare
superficie
consapevolmente la
calcolatrice e gli
strumenti informatici:
(Derive5,Geogebra,
Cabri3D).
Conoscenze
Superfici
equivalenti ed
equiscomponibili:
addizione e
sottrazione di
superfici.
Teorema di
Pitagora e teoremi
di Euclide
Principio di
Cavalieri perle
superfici :
(approfondimento)
Livello
Abilità/capacità
minimodi
conoscenzee
abilità
Disegnare figure
Riconoscere e
rappresentare
piane e ragionare
sulla loro eventuale figure
equivalenti
congruenza o
equivalenza .
Applicare le
Calcolare le aree
formule dirette
delle figure piane. peril calcolo
Utilizzare le
dell’area di un
poligono.
formule dirette e
Risolvere
inverse nella
semplici
risoluzione di
problemi.
problemi.
Il livello minimo di conoscenze e abilitàrappresenta la soglia della sufficienza anche peruna
seconda classe di biennio
61
EQUIVALENZA DELLE FIGURE PIANE
ADDIZIONE DI SUPERFICI
05-
.8
Date due superfici A e B disgiunte chiamerai sommadiA eB la superficie F.
SOTTRAZIONE DI SUPERFICI
,
"
,
"
Date due superfici Y e V chiamerai differenzadiY eV la superficie S.
SUPERFICI EQUIVALENTI O EQUIESTESE
Sappiamo giàche due figure congruenti sono sovrapponibili e quindi hanno la stessa estensione.
PROBLEM A
E’possibile che superfici non congruenti abbiano la stessa estensione?
(Disegno di un triangolo T e di un cerchio C)
Osserva le due superfici della figura: non essendo sovrapponibili,
C
in che modo puoi stabilire che hanno la stessa estensione?
Discussione da cui si possono ricavare le modalità:
-modelli dello stesso materiale hanno lo stesso peso
-serve la stessa quantitàdi colore per verniciarli
In generale:
due superfici che hanno la stessa estensione si dicono equiesteseo equivalenti
linguaggi a confronto
A parole
In simboli
T èequivalente a C
T
62
C
T
Poichénon èpratico verniciare o pesare modellini ogni volta che devo dimostrare se due superfici
sono equivalenti,saràopportuno cercare altri metodi perfarlo.
Ti ricordi di F?
Adesso ti presento D.
05/
.8
Cosa possiamo dire di F e D?
Essendo formati da parti congruenti,ricoprono la stessa parte di piano,cioèhanno la stessa
estensione: sono equivalenti.
In generale: figure come Fe D,formate da parti congruenti,si dicono equicomposte o
equiscomponibili.Figureequiscomponibilisonoequivalenti.
Facciamo costruire con la carta
Allo stesso modo:
possiamo dire che R e P sono equivalenti perchéottenute come differenza di superfici congruenti.
63
ESERCIZI
1.Osserva le figure A,B e C
e rispondi alle seguenti domande:
a)Ipoligoni A,B,e C sono congruenti?
b)Sono composti da parti congruenti?
c)Sono equivalenti?
d)Poligoni equicomposti sono sempre equivalenti?
2.Ricopia su di un foglio da lucido il rettangolo ABCD.
Taglialo lungo la linea tratteggiata nel trapezio 1 e
nel
triangolo 2.disponi le figure 1 e 2 in modo da
costruire un
triangolo,poi rispondi:
-il triangolo che hai ottenuto e il rettangolo ABCD
sono
formati da parti rispettivamente congruenti?
-puoi affermare che sono equivalenti?
Giustifica la risposta:____________________
_____________________________________
_____________________________________
_____________________________________
_____________________________________
3.Osserva le coppie di figure,poi rispondi.
64
4.Osserva le coppie di figure,poi rispondi.
a)Quali sono le coppie formate da superfici equiscomponibili?__________________
b)Quali sono le coppie formate da superfici equivalenti? ______________________
5.Osserva la figura.
Le due superfici sono equivalenti?
(prima
di
rispondere
prova
a
scomporre le due figure in parti
rispettivamente congruenti)
________________________________
________________________________
________________________________
________________________________
________________________________
6.Sai che il rettangolo ABCD è congruente al rettangolo A’B’C’D’ e che il quadrato Q è
congruente al quadrato Q’.Qual èla risposta giusta?
P e P’sono:
a congruenti
b equivalenti
c nél’uno nél’altro
65
7.Delle superfici P,R,Q e T sai che P èequivalente a R e Q èequivalente a T.
a)Costruisci (P + Q)e (R + T);verifica che tali somme sono equivalenti.
b)Costruisci (P - Q) e (R - T); tali differenze sono
8.Individua nella tabella sottostante:
a) le coppie di superfici equivalenti e congruenti: ……………………………….
.
b) le coppie di superfici equivalenti e non congruenti: ………………………….
.
9.Sai che ABC ècongruente a A’B’C’e che T ècongruente a T’.
a)Q e Q’sono:
a congruenti
b equivalenti
c nél’uno nél’altro
b)Giustifica la tua scelta:
_______________________________
_______________________________
66
equivalenti?
10. Osserva e rispondi.
Se da ogni quadrato Q togli i quattro
triangoli T, che cosa puoi dire delle
figure rimaste (quelle di colore arancio)?
____________________________
____________________________
____________________________
____________________________
Dimostrazione del Teorema di Pitagora.
11. Disegna un quadrato ABCD e congiungi il punto medio M del lato Ab con C e con D. Dimostra che il triangolo MCD è equivalente alla
metà del quadrato ABCD.
#
"
!
12. Verifica che il quadrato che ha per lato la diagonale di un quadrato è
equivalente al doppio di quest’ultimo.
13. Verifica che se in un quadrilatero le due diagonali sono perpendicolari,
la sua superficie equivale alla metà di quella del rettangolo che per
dimensioni le due diagonali.
14. Osserva la figura qui a lato:
Il trapezio ABCD è equivalente al triangolo ABE. Perché?
15. Osserva i tre poligoni rappresentati in figura e stabilisci se
sono tra loro equivalenti, giustificando la tua risposta.
67
PROBLEM A
Da una lamiera di forma rettangolare ABCD viene tagliato un triangolo FCE.
1) Quale è il rapporto tra la superficie rimasta dopo il taglio e la superficie iniziale?
2) Quale è il rapporto tra la superficie rimasta dopo il taglio e la superficie tagliata ?
68
AREA DIUNA SUPERFICIE
Sappiamo che la mi
suradi una grandezza è sempre un numero, che rappresenta il rapporto tra la grandezza
da misurare e l'
unità di misura, ossia esprime "quante volte" l'
unità di misura scelta è contenuta nella
grandezza da misurare.
Quindi se vogliamo misurare una grandezza occorre:
1) scegliere un'
unitàdimi
suraadatta, ossia una grandezza campione omogenea con quella da misurare;
2) confrontare ciò che si vuole misurare con l'
unità di misura scelta, cioè trovare il rapporto tra la
grandezza da misurare e l'
unità di misura.
In particolare, la misura di una superficie è detta areadella superficie.
L'
area di una superficie è quel numero che indica quante volte l'
unità di'misura di superficie scelta è
contenuta nella superficie da misurare.
Possiamo, quindi, dire che figure equiestese o equivalenti hanno aree uguali. (Naturalmente le aree devono
essere espresse nella stessa unità di misura.)
ESERCIZI
Negli esercizi che seguono stabilisci l’area delle figure date utilizzando le varie unità di misura assegnate.
1.
2.
3.
4.
69
LE UNITÀ DIM ISURA DISUPERFICIE
Fra tutte le figure possibili è stato scelto il quadratocome figura piùadatta ad assumere il ruolo di uni
tàdi
misuradi superficie.
Fra tutti i quadrati è stato adottato come unità di misura per le superfici il metro quadrato (m2), ossia il
quadrato che ha come lato il metro lineare.
È evidente che si useranno in modo opportuno i multipli o i sottomultipli del metro quadrato a seconda della
grandezza della figura di cui si vuole calcolare l'
area.
2
1 km
Multipli
2
1 hm
(un ettaro)
2
1 dam
(poco usato)
Principale
2
1m
Sottomultipli
2
1 dm
1 cm
2
1 mm
2
DALLA M ISURA ALLA FORM ULA:
L’AREA DEL RETTANGOLO
Quali sono, quindi, le figure geometriche di cui puoi misurare l’area? In quali figure, cioè, è possibile
stabilire quante volte l’unità di misura è contenuta nella superficie da misurare?
È evidente che, essendo un quadrato l’unità di misura della superficie, le figure di cui puoi misurare l’area
possono essere unicamente quelle che hanno solo angoli retti.
Considera il rettangolo ABCD. M isurarela sua area
significa contare il numero dei quadretti che
ricoprono interamente la sua superficie. Il numero dei
quadretti è 6, quindi diremo che la sua area è 6 cm2
(essendo ogni quadretto 1 cm2).
È facile capire che il numero totale dei quadretti è
uguale al prodotto tra il numero di quadretti di una
fila (3) e il numero delle file (2). Ma il numero dei
quadretti di una fila corrisponde alla misura del lato
AB, essendo il lato del quadretto uguale a 1 cm;così
come il numero delle file corrisponde alla misura del
lato BC.
Possiamo quindi dire che:
o si può calcolare moltiplicando la misura della base del
l’area delrettangol
rettangolo per la misura della sua altezza.
Arettangolo = b .h
Se conosciamo l’area del rettangolo e la lunghezza della sua altezza, come possiamo trovare la sua base?
Poiché
è il percorsodirettoper trovare l’area conoscendo le lunghezze dei lati
è il percorso inverso per trovare la base conoscendo l’area e la lunghezza
dell’altezza.
Analogamente si avrà:
70
Riassumendo:
Arettangolo =b . h
b=
A
h
h=
A
b
ESERCIZIdiBASE
1. Calcola l'
area di un rettangolo avente la base e l'
altezza lunghe rispettivamente 17,8 cm e 253 mm.
2. Calcola perimetro e area di un rettangolo le cui dimensioni misurano rispettivamente 63 cm e 51 cm.
3. L'
area di un rettangolo è di 390cm2 e l'
altezza misura 25 cm. Calcola il perimetro.
[81,2cm]
3
4. In un rettangolo la base misura 35 m e l'
altezza è i della base. Calcola perimetro e area.
7
[100m;525 m2]
5. Internamente a un cortile di forma rettangolare si ricava un'
aiuola, anch'
essa rettangolare, avente il
7
di tutto il cortile. Per la sistemazione del
perimetro di 40 m e larga 13 m e la cui superficie copre i
15
muro perimetrale di questo cortile si spendono 4,7 € il metro;quale spesa si sostiene per questa
sistemazione sapendo che il cortile è largo 25 m?
[308,32 €]
L’AREA DEL QUADRATO
Sappiamo che il quadrato è un rettangolo avente le due dimensioni uguali. Da
questo si ricava che:
l’areadelquadratosi calcola elevando alla seconda potenza la misura del
lato.
Aquadrato = l2
Supponiamo di conoscere l’area del quadrato e di voler calcolare il valore del
lato. Sappiamo che l’operazione inversa dell’elevamento a potenza è
l’estrazione di radice.
Poiché
del
è il percorsodi
rettoper trovare l’area del quadrato conoscendo la lunghezza
lato
è il percorsoinversoper trovare la lunghezza del lato conoscendo l’area.
Riassumendo:
Aquadrato =l2
71
l= A
ESERCIZIdiBASE
1. Il perimetro di un quadrato è di 96 cm, calcola l'
area.
2. L'
area di un quadrato è di 182,25 cm2, calcola il perimetro.
3. Un quadrato è isoperimetrico ad un rettangolo in cui la differenza delle dimensioni misura 35 cm e una è
7
i dell'
altra. Calcola perimetro e area delle due figure.
[126 cm;992,25 cm2;686 cm2]
2
4. Un quadrato ha l'
area di 3600 cm2. Calcola l'
area di un rettangolo avente il perimetro uguale ai
quello del quadrato e la base i
5
dell’altezza.
4
9
dì
8
[4500cm2]
5. Lungo il muro perimetrale di un terreno di forma quadrata sono stati piantati, alla distanza di 0,5 m
ciascuno, dei paletti che sono costati 2,35 €ciascuno. Se la spesa complessiva è stata di 2350€, quanto
misura la superficie del terreno?
[15625 cm2]
72
L’AREA DEL PARALLELOGRAM M A
Se la figura non ha solo angoli retti non è possibile misurare la sua superficie utilizzando l’unità di misura
convenzionale.
È però possibile determinare la sua area ricorrendo ai principi di equivalenza;si tratta di trovare un
rettangolo equivalente alla figura data: calcolando l’area di questo rettangolo si determina anche l’area della
figura.
Vediamo come è possibile calcolare l’area del parallelogramma.
Il parallelogramma ABCD e il rettangolo
B’BHH’ sono equivalenti perchè sono figure
equicomposte. L’area del parallelogramma è
quindi uguale all’area del rettangolo;inoltre
la base del parallelogramma è congruente
alla base del rettangolo e l’altezza del
parallelogramma è congruente all’altezza del
rettangolo.
Abbiamo perciò:
Aparallelogramma = Arettangolo = AB . BH
Pertanto possiamo dire che:
l’areadelparal
lelogrammasi calcola moltiplicando fra loro la misura della base
per la misura dell’altezza.
Analogamente a quanto già visto per il rettangolo, possiamo riassumere:
Aparallelogramma =b . h
b=
A
h
h=
A
b
ESERCIZIdiBASE
1. In un parallelogramma la base misura 27 cm e l'
altezza relativa supera la base di 3,5 cm. Calcola l'
area
del parallelogramma.
[823,5 cm2]
2. Un quadrato, un rettangolo e un parallelogramma sono equivalenti. L'
altezza del rettangolo misura 24 cm
9
6
e la base è i suoi ;la somma delle altezze del parallelogramma misura 110 cm e sono una i
4
5
dell'
altra. Calcola il perimetro delle tre figure.
[144 cm;156 cm;95,04 cm]
73
L’AREA DEL TRIANGOLO
Osserva il triangolo ABC e il rettangolo ABDE.
È evidente che:
-il triangolo è equivalente alla metà del rettangolo
- la base del triangolo è congruente alla base del
rettangolo
- l’altezza del triangolo è congruente a quella del
rettangolo.
Per determinare l’area del triangolo basta calcolare
l’area del rettangolo e dividerla per due.
Quindi:
l’area deltriangolo si calcola moltiplicando la misura della base per la misura
dell’altezza e dividendo il prodotto per due.
Atriangolo =
b⋅h
2
Supponiamo di conoscere l’area del triangolo e la misura della sua altezza e di voler determinare la misura
della base.
è il percorso diretto per trovare l’area conoscendo la base e
l’altezza
Poiché
è il percorsoinversoper trovare la base conoscendo l’area e la
lunghezza dell’altezza.
Analogamente si avrà:
Riassumendo:
Atriangolo =
b⋅h
2
b=
2A
h
h=
2A
b
ESERCIZIdiBASE
1. In un triangolo la base misura 39 cm ed è i
3
dell'
altezza. Calcolane l'
area.
4
[1014 cm2]
2. Un triangolo ha l'
area di 493 cm2 e la base lunga 29 cm. Calcola la misura dell'
altezza
3. In un triangolo rettangolo i cateti e l'
ipotenusa misurano 18 cm, 80 cm e 82 cm. Calcola la misura
dell'
altezza relativa all'
ipotenusa.
[17,56 cm]
4. L'
area di un triangolo rettangolo è di 60,75 cm2e un cateto è i
avente il lato congruente al cateto maggiore del triangolo.
74
2
dell'
altro. Calcola l'
area diun quadrato
3
[182,25 cm2]
5. Un triangolo ha il perimetro di 270 cm e due lati lunghi rispettivamente 95 cm e 97 cm. Calcola il
2
perimetro di un rettangolo equivalente ai del triangolo e avente una dimensione lunga 60cm.
3
[196 cm]
L’AREA DEL ROM BO
Il rombo è un particolare parallelogramma, quindi la sua area può essere
calcolata utilizzando la formula vista in generale per i parallelogrammi:
Arombo =l . h
Il rombo inoltre è caratterizzato dal fatto di avere le diagonali perpendicolari. La sua area si può quindi
determinare anche in un altro modo.
Osservando le figure ti puoi facilmente convincere che il
rombo ABCD è equivalente alla metà del rettangolo EFGH:
l'
area del rombo sarà quindi la metà dell'
area del rettangolo.
Le dimensioni del rettangolo sono congruenti alle diagonali
del rombo, quindi possiamo affermare che:
area del rombo si trova moltiplicando tra loro le
l'
lunghezze delle diagonali e dividendo il prodotto per due.
Arombo =
d1 ⋅ d 2
2
è il percorso di
retto per trovare l’area del rombo conoscendo le
lunghezze delle diagonali
Poiché
è il percorsoinversoper trovare una diagonale conoscendo l’area e
lunghezza dell’altra diagonale.
la
Riassumendo:
Arombo =
d1 ⋅ d 2
2
d1 =
75
2A
d2
d2 =
2A
d1
L’AREA DEIQUADRILATERICON LE DIAGONALIPERPENDICOLARI
L’area di un qualsiasi quadrilatero con le diagonali
perpendicolari può essere determinata con la stessa
formula vista per il rombo.
A=
d1 ⋅ d 2
2
In particolare, l
’area delquadrato potrà essere calcolata anche in
questo modo:
Aquadrato =
d ⋅d d2
=
2
2
da cui, con percorso inverso si avrà:
poiché: Aquadrato = l2
d = 2A
si ottiene:
d =l 2
ESERCIZIdiBASE
1. In un rombo la diagonale maggiore misura 48 cm ed è gli
2. In un rombo un lato misura 28 cm ed è i
rombo.
8
della minore. Calcolane l’area. [720cm2]
5
7
dell'
altezza ad esso relativa. Calcola il perimetro e l'
area del
5
[112cm;560cm2]
3. II lato di un rombo misura 25 cm e la sua distanza dal lato opposto misura 24 cm. Calcola la misura della
diagonale minore sapendo che la maggiore misura 40cm (la distanza fra due lati opposti coincide con..)[30cm]
4. Un rombo ha l'
area di 120 cm2 e le due diagonali una i
diagonali.
5
dell'
altra. Calcola la misura delle due
3
[20cm;12 cm]
5. Le diagonali di un quadrilatero sono perpendicolari e tali che la loro somma misura 65 cm. Sapendo che
3
sono una i dell'
altra, calcola l'
area del quadrilatero.
[507cm2]
2
76
L’AREA DEL TRAPEZIO
Osserva il trapezio ABCD e il
parallelogramma AD’A’D.
È evidente che:
-il trapezio è equivalente alla metà
del parallelogramma
- la base del parallelogramma è
congruente alla somma delle basi del
trapezio
-l’altezza del trapezio è congruente a
quella del parallelogramma.
Per determinare l’area del trapezio basta calcolare l’area del parallelogramma e dividerla per due.
Quindi:
l’area deltrapezio si calcola moltiplicando la somma delle lunghezze delle basi
per la misura dell’altezza e dividendo il prodotto per due.
Atrapezio =
(bM
+ bm ) ⋅ h
2
Le formule inverse sono le seguenti:
(bM
+ bm ) =
2A
h
h=
2A
(bM + bm )
ESERCIZIdiBASE
1. In un trapezio la base minore misura 15 cm, la maggiore è il triplo della minore e l'
altezza misura 8 cm.
Calcola l'
area.
[240cm2]
7
della
4
[385 cm2]
2. In un trapezio la differenza fra la base minore e la base maggiore misura 15 cm e la maggiore è i
minore. Sapendo che l'
altezza misura 14 cm, calcola l'
area del trapezio.
3. In un trapezio l'
area è di 247 cm2 e le due basi misurano rispettivamente 16 cm e 22 cm. Calcola la
misura dell'
altezza.
[13 cm]
4. In un trapezio la differenza fra le due basi misura 60cm e una è i
3
della loro somma, calcola l'
area del trapezio.
10
5
dell'
altra. Sapendo che l'
altezza è i
2
[2940cm2]
5. Il trapezio rettangolo ABCD è stato diviso dal segmento EF, parallelo all'
altezza, in due
2
parti fra loro equivalenti. Se l'
area del trapezio è 3075 cm e le due basi misurano
rispettivamente 62,5 cm e 40cm, quanto misura la base del rettangolo ABFE?
[25,625 cm]
77
6. Il trapezio rettangolo ABCD è stato diviso in due partìmediante il segmento EF,
parallelo al suo lato obliquo e passante per il punto medio della base maggiore.
Sapendo che le due basi del trapezio misurano rispettivamente 51 cm e 76,5 cm e che
l'
area è di 1625,625 cm2, calcola le aree delle due parti.
[975,375 cm2;650,25 cm2]
78
*+,
-,
%./,
0.#0.#,
%.
%
1
.
%
!%
%
"
<<<<<<<<<<<<<<<
.9
l9
<<<<<<<<<<<<<<<
.9
b9
h9
<<<<<<<<<<<<<<<
.9
b9
h9
<<<<<<<<<<<<<<<
.9
b9
h9
<<<<<<<<<<<<<<<
.9
d9
D9
<<<<<<<<<<<<<<<
.9
h9
B + b9
%
3
/
5
"$
5
1
4 55
"
=3
&
4
$
"
>
*6
>
-6
6
/
"6
%
?
3
6
=3
&
4
"
6
/
5
6
1
"4 55
"
6
=3
4
&
6
=3
55
!
!
56
-
5
6
,
4
3
?
3
@
6
1
5
3
'!7
)
79
*+,
-,
%./,
0.#0.#,
%.
%
1
.
%
&
"
!%
,
) %
2
)
,
"
!
3
4
%
3
%
2
" 5 5 ' )
1
5
2
!
2
!
"
5
(
2
%
6
"
7
"6
2
4
"
,
"
3
.89!
8%9)
-98%9/:
;9%/9.89$;
.9(
80
!
!"
!
!
!
#
$
%
&
"
'
'"
(
("
)
#
81
FILE GEOGEBRA SCARICABILI
DALLA RETE INTERNET
www.itsosgadda.it
82
COSTRUZIONE DEI QUADRATI DI NUMERI INTERI
Su di un foglio quadrettato scegli la tua unità di misura u:
•
•
•
•
•
•
Costruisci successivamente : un quadrato di lato u ,2 u, 3u,
4u..
Cosa osservi rispetto alle aree?
Se raddoppio il lato , l’area raddoppia? … … ..
E’ il … … … …
Bene probabilmente sarai d’accordo nel ritenere peròche esiste un quadrato di area
doppia!!
Allora il suo lato l sarà compreso tra 1 e 2 cioè 1< l < 2
Come possiamo costruirlo?
Vai al file geogebra :Costruzione di un quadrato di area doppia
83
COSTRUZIONE DEL QUADRATO DI AREA DOPPIA
•
•
•
•
•
Su di un foglio quadrettato scegli una unità di misura u
Costruisci un quadrato di lato di lato u
Traccia la diagonale AC
Costruisci ora un quadrato che ha per lato la diagonale AC
Confronta l’area dei due quadrati ABCD e ACEF ;cosa osservi ?
Abbiamo risolto il problema :
L’ area del quadrato ACEFè doppia dell’area del quadratoABCD
Vai al file geogebra : quadrato di area doppia
84
COSTRUZIONE DELLA CHIOCCIOLA DEGLI IRRAZIONALI
•
•
•
•
•
Su di un foglio quadrettato scegli una unità di misura u
Costruisci un quadrato di lato di lato u
Traccia la diagonale
Costruisci un triangolo rettangolo che ha per cateto maggiore AC ,la diagonale del quadrato,
per cateto minore CE ,unità di misura u :l’ipotenusa del triangolo AE = 3
Si ripete il procedimento ,costruendo un nuovo triangolo rettangolo come da figura.
Ogni ipotenusa dei triangoli rettangoli ossia : AC, AE,AF,AG,AH… rappresenta
un numero intero o un numero irrazionale .
NB Osservazioneimportante!!! Il software Geogebra , approssima i numeri irrazionali
con numeri decimali (qui con due cifre decimali ) quindi li rende razionali!!.
85
COSTRUZIONE DI NUMERI IRRAZIONALI COME APPLICAZIONE
DEL 2°TEOREMA DI EUCLIDE
•
•
•
•
•
•
•
Costruisci una semicirconferenza di diametro AB
Prendi un punto C sulla semicirconferenza
Considera il triangolo ABC ,che triangolo hai ottenuto?
Traccia l’altezza CH relativa ad AB e applica il 2°Teorema di Euclide.
CH = AH *HB
Muovi il punto H , il punto C è vincolato alla semicirconferenza
1
Le altezze CH rappresentano numeri irrazionali tali che 0≤ CH ≤ AB
2
86
EQUIVALENZA RETTANGOLO –PARALLELOGRAMMA
•
•
•
•
Su due rette parallele a1 e d costruisci un rettangoloABCD
Costruisci il parallelogrammaABFE
Di questi due quadrilateri ne esiste uno di area maggiore?
Motiva la risposta
Vedi l’animazione nel file Geogebra :EquivalenzaRettangolo –Parallelogramma
87
COSTRUZIONE DI UN TRIANGOLO EQUIVALENTE A META’ DEL
PARALLELOGRAMMO
•
•
•
•
•
•
•
Traccia due rette parallele
Costruisci il triangolo ABC
Prendi il punto medio D di CB
Costruisci il triangolo CBA’ simmetrico di ABC rispetto a D
Traccia l’altezza CE
Cosa osservi?
Il triangolo ABC è equivalente a metà del parallelogrammo
Vedi l’animazione nel relativo file Geogebra :Triangolo-parall
88
EQUIVALENZA TRAPEZIO-TRIANGOLO
•
•
•
•
Costruisci trapezio ABCD
Costruisci il punto medio E di BC
Costruisci il simmetricoEBD’ del triangolo DCE rispetto ad E
Confronta il trapezio ABCD e il triangolo ADD’come sono?
Vedi l’animazione nel relativo file Geogebra: Equivalenza Trapezio-triangolo
89
COSTRUZIONE DI UN POLIGONO DI LATI N-1 DA UN POLIGONO DI N LATI
Dato un poligono di n lati ,costruirne uno equivalentecon n-1 lati
Prendiamo un pentagono ABCDE come possiamo costruire un quadrilatero equivalente?
•
•
•
•
•
Costruiamo la diagonale AD
Dal punto E conduciamo la retta parallela ad AD
Prolunghiamo il lato AB fino ad intersecare la parallela nel punto G
Congiungo D con G ottenendo il quadrilatero cercato.
Confronta i poligoni ABCDE ed GBCD perché sono equivalenti?
Vedi l’animazione nel relativo file Geogebra :Poligoni con lati n-1
90
PRIMO TEOREMA DI EUCLIDE
• Costruisci una semicirconferenza di diametro AB
• Prendi su di essa il punto C
• Costruisci il triangolo rettangolo ABC
• Costruisci il quadrato di lato AC
• Costruisci il rettangolo di lati AE (proiezione del cateto AC sull’ipotenusa ) e AH
congruente ad AB
• Cosa osservi?
Vedi l’animazione nel file Geogebra : I°Teorema di Euclide
91
TEOREMA DI PITAGORA
• Costruisci una semicirconferenza di diametro AB
• Prendi su di essa il punto C
• Costruisci il triangolo rettangolo ABC
Oppure : Costruisci un triangolo rettangolo ABC di ipotenusa AB
• Costruisci il quadrato di lato AC
• Costruisci il rettangolo di lati AK (proiezione del cateto AC sull’ipotenusa ) e AI congruente
ad AB
• Costruisci il quadrato di lato CB
• Costruisci il rettangolo di lati KB(proiezione del cateto CB sull’ipotenusa ) e BJcongruente
ad AB
Hai cosìapplicato il 1°Teorema di Euclide ai due cateti AC e CB
Cosa osservi? Muovi il punto C
Vedi l’ animazione nel relativo file Geogebra: Teorema di Pitagora
.
92
SECONDO TEOREMA DI EUCLIDE
Costruisci il triangolo rettangolo ABC come segue:
• traccia una semiretta di origine A
• traccia un segmento AC come cateto
• traccia dal punto C la perpendicolare al lato AC
• sia B il punto intersezione con la semiretta
• Traccia l’altezza CD relativa all’ipotenusa AB
• Costruisci il quadrato di lato CD
• Costruisci il rettangolo che ha per lati AD (proiezione di AC su AB)
e AH (congruente a DB che è la proiezione di CB su AB)
• Cosa osservi?
Vedi animazione nel relativo file Geogebra : 2°Teorema di Euclide
93
INDICAZIONI METODOLOGICHE sull’uso
deglistrum entiinform atici
DERIVE
E’un software molto potente con cui si possono affrontare tutti gli argomenti
matematici di un curricolo che parte dalla scuola media fino a una qualsiasi
facoltà scientifica: esso sviluppa infatti il calcolo algebrico, l’insiemistica, la
logica, il calcolo letterale, la statistica, l’algebra lineare, il calcolo differenziale
ed altro. E’ strutturato in pagine di calcolo e pagine di rappresentazioni in R 2 e
in R 3 tra di loro efficacemente comunicanti. Si possono agevolmente esportare
porzioni di queste pagine nei più comuni documenti realizzabili con
videoscrittura e trattamento dell’immagine. Nella scuola superiore assolve un compito formativo
importante se affiancato al curricolo tradizionale in ogni suo passo, in modo che alla fine lo
studente universitario o il tecnico si trovi padrone di questo sofisticato strumento di calcolo.
Nella scuola media, esso può essere di grande aiuto all’insegnante
che voglia produrre numerosi esercizi semplici, monotematici,
specifici, ad esempio, per un’attività di recupero. In questo
contesto, dove la semplicità del calcolo e la lotta quotidiana per
l’uso corretto della calcolatrice sono di casa, esso appare meno
utile come strumento in mano agli alunni. In nessun modo esso
deve sostituire la pratica del calcolo con mezzi tradizionali.
94
GEOGEBRA
Questo software è molto utile sia per lo studio della geometria piana che della
geometria analitica. E’ scaricabile gratuitamente dalla rete, per cui può far parte
facilmente della dotazione informatica di qualunque scuola e di qualunque alunno
che possieda un computer. Oltre alla verifica empirica di teoremi, si possono
effettuare costruzioni geometriche anche di grande complessità. E’ possibile
produrre animazioni automatiche e figure geometriche le cui caratteristiche
dipendano da uno o più parametri modulati con continuità da barre di scorrimento. E’ possibile
produrre figure geometriche quotate (misure lineari e angolari) ed ottenere la stampa fedele di esse
(con misure reali). L’insegnante può cosìpredisporre un’attività consistente nella risoluzione di
figure geometriche in modo che gli alunni verifichino direttamente, misurando, ogni risultato
parziale ottenuto. In nessun modo questo software deve sostituire il disegno geometrico realizzato
con metodi tradizionali.
E’ possibile esportare le immagini in vario modo;preziosa è la facoltà di realizzare finestre attive di
pagine web con una procedura molto semplice. Una finestra di dialogo consente l’introduzione di
dati numerici e di funzioni che possono essere elaborati sia in modo analitico che grafico.
95
CABRI3D
Questo software, affascinante ma non semplicissimo da utilizzare, consente la
realizzazione di oggetti geometrici immersi in uno spazio virtuale a tre
dimensioni. Esso è di grande aiuto per familiarizzare con rette, piani, angoli
diedri e triedri;si possono creare altresìsolidi di vario tipo, inclusi i poliedri
platonici. Consente l’identificazione di figure nate dall’intersezione di piani con
solidi di cui sopra e la realizzazione delle principali simmetrie. Si puòesportare
la pagina con grande precisione in un software per il trattamento dell’immagine. E’ l’ideale per i
ragazzi di oggi, già pratici del mondo virtuale. In nessun modo questo software deve sostituire lo
studio di solidi reali, realizzati in modo artigianale.
96
La storia della m atem atica nelcurricolo
tradizionale.
Quando si insegna la Matematica senza fare alcun cenno all’origine storica dei vari argomenti, si
lascia inconsapevolmente intendere che essa sia, per propria natura, immutabile, vera, esatta: ciò
non corrisponde al vero, nonostante essa sia un potentissimo mezzo di indagine e di conoscenza.
La matematica nasce in ogni essere pensante e nella storia dell’umanità, principalmente come
osservazione del mondo circostante e, come qualsiasi altra espressione dell’ingegno umano, porta
con sé incertezze, incongruenze, errori.
I concetti che noi esponiamo, cosìpuliti, cristallini, verificabili, sono tali perché hanno subito nei
secoli un rodaggio e una rielaborazione continui;il valore di questa colossale opera di sintesi non
deve essere perduto.
E’ tuttavia difficoltoso trattare la Storia della Matematica in un curricolo tradizionale a causa della
vastità dell’argomento: solo considerando quanto avvenuto nel continente eurasiatico, si debbono
tenere presenti cinque o sei millenni di storia costituita da centinaia di rivoli che nascono,
confluiscono e si separano in continuazione, intrecciati al resto delle contingenze che costituiscono
la vicenda umana. I testi più affidabili sono ponderosi e di difficile consultazione proprio perché
non è possibile trovare in essi un’unica trama evolutiva.
La semplice collocazione storica degli argomenti, corredata dal racconto di qualche episodio
(importante o bizzarro) aiuta sicuramente lo studente a considerare la materia in questa nuova e
assai piùrealistica ottica. Alcuni aspetti meritano forse maggiore attenzione:
Problemipraticieconcettiastratti.
Esistono due situazioni spesso in conflitto tra di loro: risolvere un problema pratico ottenendo
rapidamente il risultato cercato nei limiti di una ragionevole precisione, oppure trattare con rigore
logico una questione non immediatamente riconducibile ad una situazione reale.
Se devo misurare la diagonale di un quadrato unitario posso semplicemente dire che essa è circa
1.41 metri: nessun sarto, falegname o vetraio avrà nulla da ridire in merito.
La natura del numero capace di esprimere in modo esatto la misura di tale diagonale non è semplice
e ha dato origine ad una discussione durata secoli.
Sìpuò dire che l’approccio astratto (sintattico) riporta ai matematici e filosofi del mondo Greco
Classico, per i quali i problemi pratici erano del tutto privi di interesse, mentre l’altro (semantico)
ha ottenuto maggiore dignità nel mondo Ellenistico (Alessandrino).
Si puòavere una maggiore propensione verso l’uno o l’altro approccio, tuttavia la Matematica vive
di essi in uguale misura;lo studente dovrebbe almeno avere la consapevolezza dell’ambito nel quale
egli si trova volta per volta.
97
Lanascitadiunateoriaelasuaformalizzazione
Quando trattiamo argomenti di Geometria Razionale, lo facciamo ancora oggi seguendo la traccia
lasciata dagli “Elementi” di Euclide: si tratta di tredici libri nei quali sono elencate 467
proposizioni, dimostrate secondo i canoni della logica aristotelica ed esposte con un linguaggio
specifico che si forma al procedere della trattazione. Euclide era un insegnante e la sua opera
preziosa è consistita principalmente nell’aver riordinato e formalizzato il sapere matematico
prodotto nei secoli precedenti.
E’ accaduto qualcosa di simile nel diciottesimo secolo: idee geniali ma disordinate che Newton
ebbe nel risolvere il problema delle leggi del moto e che Leibniz riscrisse (forse) con notazioni più
efficaci, produssero un fiorire caotico di studi, insieme ad una famosa diatriba tra il mondo
accademico continentale e quello britannico.
Dopo un secolo, l’intera materia era poco comprensibile e zeppa di paradossi: nacque una
associazione di matematici (il Movimento Critico) che, come fece Euclide, riscrisse l’intera teoria
come oggi la conosciamo: l’Analisi Matematica, limpida come un cristallo.
Lo studente dovrebbe trarre questo insegnamento: l’ordine, l’accuratezza del linguaggio, la
precisione non servono per avere idee geniali, tuttavia essi sono indispensabili per metterle in
pratica e soprattutto per comunicarle al prossimo.
Numeridecimaliescritturadeinumeri
I numeri decimali sono importanti perché permettono di effettuare calcoli con le comode tecniche
del calcolo posizionale che risulta essere molto piùcomodo del calcolo frazionario.
1
A noi sembra normale pensare a
come a 0, ma non è stato sempre così.
2
Nel XVI secolo troviamo ancora i contabili alle prese con il calcolo delle frazioni, essi dispongono
di “regole” e trucchi, ma il calcolo con le frazioni resta complicato, richiede un addestramento
particolare e quindi non è alla portata di tutte le persone che devono eseguire calcoli tecnici,
commerciali…
In questo stesso periodo stanno avvenendo profonde trasformazioni: si scoprono terre nuove, si lotta
per la libertà religiosa e di pensiero, si sviluppano nuove tecnologie (stampa 14, polvere da sparo,
partita doppia nella contabilità… .) si sente quindi la necessità di snellire i calcoli per migliorare il
commercio, intralciato tra l’altro dalle differenti misure nelle monete e nei pesi,
diversi da paese a paese.
Uno dei primi sostenitori delle frazioni decimali è stato il matematico F.Viete (1540 -1603)nel suo
libro Canon Mathematicus 1579. Pochi anni dopo,la rappresentazione decimale delle frazioni è
stata “inventata” dall’ingegnere e fisico svizzero Simon STEVIN nel 1585, nelsuo trattato
“DeThiende(la decima), che propose la scrittura decimale posizionale dei numeri non interi;la
notazione odierna, però, giunse due secoli dopo e ancora oggi ci sono vari modi;in Gran Bretagna
si usa il punto a mezza altezza, negli Stati Uniti il punto 2.3, da noi la virgola.
Prima del 1600 si usavano le frazioni senza eseguire la divisione tra numeratore e denominatore.
Nell’antichità ogni popolo, a seconda del proprio sistema di numerazione, adottò un calcolo
frazionario diversi: i calcoli erano comunque laboriosi e necessitavano di tavole di vario tipo, erano
eseguiti dagli scribi e non erano alla portata di tutti.
98
Lefrazionidinumeroeildiosmembrato
Nella “Storia universale dei numeri”di G. Ifrah (editore Mondadori) troviamo:
Per esprimere le frazioni, gli egizi si servivano, in genere, del
geroglifico della bocca (segno che si leggeva,
che, nel contesto,
significava «parte») e lo mettevano sopra il numero facente funzione
di denominatore:
Quando il denominatore non poteva venire rappresentato tutto intero
sotto il segno della «bocca», essi
scrivevano l'
eccedenza di seguito:
Alcune frazioni, come 1/2, 2/3 e 3/4, erano raffigurate con segni speciali.
1
2
2
3
3
4
Si leggeva GeS ed esprimeva l'
idea della metà.
Letteralmente: “le due parti”.
“le tre parti”
Queste due ultime espressioni non erano affatto concepite come frazioni: gli egizi non conoscevano
le frazioni con il numeratore diverso da 1.
Per esprimere, ad esempio, la quantità 3/5 usavano i simboli pari a 1/2 + 1/10La frazione 47/60si
scomponeva così: 47/60= 1/3 + 1/4 + 1/5.
Gli Egizi avevano quindi bisogno, per eseguire il calcolo con le frazioni, di “tavole”(vedi disegno)
sulle quali leggere le scomposizioni di ogni frazione di uso comune, in somma di frazioni con
numeratore 1, in modo che il numero di queste frazioni fosse il piùpiccolo possibile.
Nella pagina successiva troviamo un manoscritto matematico (in cuoio) redatto in caratteri ieratici
egizi.
Si tratta di una tavola di conversione di frazioni in somme di frazioni con numeratore uguale a 1,
che gli scribi contabili usavano frequentemente in diverse operazioni aritmetiche. -British Museum.
99
Numeridecimaliescritturadeinumeri
Un esempio significativo dell’importanza che, presso gli Egizi aveva chi sapeva eseguire i calcoli
con le frazioni e piùin generale del collegamento tra magia, religione e matematica è rappresentato
dalla leggenda relativa al dio Horus.
Le frazioni: 1/2, 1/4, 1/8, 1/16, 1/32 e 1/64 erano sottomultipli dell’ heqat(unità di misura delle
capienze,pari,secondo la stima tradizionale fatta da G. Lefebvre,a circa 4,
785litri
Queste frazioni erano rappresentate in modo particolare e la loro unione dava il disegno magico
dell’occhio che il dio Horus, secondo la leggenda, aveva perso combattendo per vendicare la morte
del padre.
Il dio Thot, dio dei sapienti e dei maghi, aveva trovato tutte le parti dell’occhio di Horus, eccetto
una, la piùpiccola. Ricomponendo le parti si ottiene: 1/2+1/4+1/8+1/16+1/32+1/64=63/64.
Narra la leggenda che la parte mancante per formare l’unità (1/64), viene data dal
dio Thot al contabile che si pone sotto la sua protezione come portafortuna
nell’esecuzione dei calcoli…
Ricordiamo che il sistema di notazione descritto fu correntemente usato nei papiri
redatti in caratteri ieratici ma che, ad eccezione del segno usato per 1/2, questi simboli non
appaiono sulle iscrizioni geroglifiche lapidarie, se non all'
inizio della XX dinastia.
100
D'
altronde gli egizi usarono altri sistemi di notazioni frazionarie, in particolare per esprimere misure
di lunghezza e di superficie e anche per misure ponderali.
Non è qui il caso di esaminare tali notazioni (riguardanti per lo più il campo metrologico), e
rinviarne il lettore alla grammatica di S.A. Gardiner e ai lavori di K. Sethe.
Nel tempo il modo di scrivere le frazioni è cambiato: l’attuale modo proviene dall’India dove verso
2
2
per indicare
.
il 1000d.C. i matematici cominciarono a scrivere
3
3
Gli Arabi introdussero la linea di frazione e questa si trova già indicata nei manoscritti latini del
Medioevo.
BIBLIOGRAFIA
J.P. Delahaye
Stupefacenti numeri primi
Ghisetti e Corvi
A. Frajese
Attraverso la storia della matematica
Le Monnier
M. Kline
Storia del pensiero matematico
Einaudi
M. Tahan
L’uomo che sapeva contare
Salani
Autori vari
Enciclopedia delle matematiche elementari
Materiali provenienti dal corso di formazione mat@bel :
“ Frazioni in movimento” e “ Dalla frazione al numero decimale”.
101
Pagine
Indice
INUMERI.......................................................................................................................................................................... 1
Laboratorio 1
L’unitàfrazionaria............................................................................................................................. 2
Laboratorio 2
Le frazioni e le loro operazioni ......................................................................................................... 5
Rappresentazione sulla retta numerica di frazioni di unità–metodo grafico ................................................................. 9
Esercizi di base con DERIVE 6................................................................................................................................... 10
Laboratorio 3 Dalla frazione al numero decimale.................................................................................................... 12
RICHIAMITEORICI
......................................................................................................................................... 18
Dalla frazione al numero decimale ............................................................................................................................... 20
Dalla frazione alla frazione decimale ........................................................................................................................... 21
Dalla frazione decimale al numero decimale ................................................................................................................ 21
Dal numero decimale alla frazione decimale ................................................................................................................ 21
ESERCIZI
Rappresentazione di numeri sulla retta numerica .............................................................................. 29
APPROFONDIMENTO Inumeri periodici ................................................................................................................ 31
DAINUMERIPERIODICIAINUMERIIRRAZIONALI......................................................................................... 32
Laboratorio n°1 Piegatura del foglio A4.................................................................................................................. 32
Laboratorio n°2
Quadrato di area doppia................................................................................................................. 33
Laboratorio n°3 Rappresentazione di numeri irrazionali ......................................................................................... 36
Laboratorio n°4 “Chiocciola dei numeri” ............................................................................................................... 36
Laboratorio n°5 Caccia alle terne pitagoriche.......................................................................................................... 37
Laboratorio n°6 «… i matematici sono persone sensibili… ».................................................................................. 38
NUMERIREALIE OPERAZIONI.............................................................................................................................. 41
GEOMETRIA PIANA...................................................................................................................................................... 61
EQUIVALENZA DELLE FIGURE PIANE................................................................................................................ 62
AREA DIUNA SUPERFICIE..................................................................................................................................... 69
LE UNITÀ DIMISURA DISUPERFICIE.................................................................................................................. 70
DALLA MISURA ALLA FORMULA: ....................................................................................................................... 70
L’AREA DEL RETTANGOLO ................................................................................................................................... 70
L’AREA DEL QUADRATO........................................................................................................................................ 71
L’AREA DEL PARALLELOGRAMMA .................................................................................................................... 73
L’AREA DEL TRIANGOLO....................................................................................................................................... 74
L’AREA DEL ROMBO
......................................................................................................................................... 75
L’AREA DEIQUADRILATERICON LE DIAGONALIPERPENDICOLARI........................................................ 76
L’AREA DEL TRAPEZIO ......................................................................................................................................... 77
FILE GEOGEBRA SCARICABILI................................................................................................................................. 82
INDICAZIONIMETODOLOGICHE SULL’USO DEGLISTRUMENTIINFORMATICI.......................................... 94
LA STORIA DELLA MATEMATICA NEL CURRICOLO TRADIZIONALE............................................................. 97
BIBLIOGRAFIA............................................................................................................................................................ 101
102