F3_esame_26-11

Cognome e nome:
A.A. 2007/2008 Modulo di Fisica 3 Meccanica e A.&T.
PROVA D’ESAME (26/11/2007)
Luogo e data di nascita
Corso di laurea
Matricola
1- Una sfera di raggio r= 2 cm e massa m = 0,1 kg è fissata all’estremo inferiore di una sottile
sbarra anch’essa di massa m e lunghezza l = 20 cm. L’intero sistema può oscillare intorno a un
asse orizzontale, a, posto alla distanza l/4 dall’estremo inferiore della sbarra. Determinare il
periodo delle oscillazioni di piccola ampiezza.
2. Un recipiente, contenente acqua, si muove con un’accelerazione di modulo pari all’accelerazione di
gravità e di direzione formante un angolo di 60° rispetto alla verticale, verso il basso. Determinare : A)
Modulo, direzione e verso che dovrebbe avere una forza resistente applicata ad un corpo di volume pari a
100 cm3 e massa 80 g, immersa nell’acqua, affinché si muova di moto rettilineo uniforme rispetto al
recipiente ; B) l’orientazione della superficie libera del liquido rispetto all’orizzontale.
a
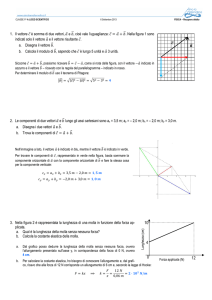
3) Una fune tesa fissata alle proprie estremità. Sapendo che la lunghezza e la massa della corda sono
rispettivamente L=80 cm e m=20 g, calcolare la tensione T2 che occorre applicare alla corda affinché la
frequenza dell’armonica fondamentale sia f2 = 220 Hz.
4) Ricordando che la temperatura di ebollizione dell’acqua è 100° C alla pressione p=1 atm, calcolare la
variazione di energia libera di Helmholtz e di energia interna corrispondenti alla condensazione di
m=5g di vapore, sapendo che il calore latente di evaporazione è =2.2 106 J/kg mentre la densità del
vapor d’acqua a 100 °C è 0.55 kg/m3 .
Ricavare inoltre dT/dp, la variazione della temperatura di ebollizione per piccole variazioni della
pressione.
Soluzioni della prova del 26/11/07
1. Il momento d’inerzia del sistema rispetto all’asse di sospensione è
2
2
2
l
 ml
l
I O  mr  m  r  
 m  = 1.09x10-3 kg m2.
12
4

4
l
l

L’equazione dei momenti si scrive : I O   mg   r  sen   mg sen   0
4
4

2
5
2
I0
= 1.48 s.
mgr
2) A) Nel sistema di riferimento solidale col recipiente, la risultante delle forze di
volume e della spinta di Archimede sul corpo è :
FT = (l - c) (at - g)V il cui modulo è : |FT| = (l - c ) 2gCos(60)V  0.2 N
La forza resistente FR dovrà avere modulo pari a FT ma verso opposto.
B) la superficie libera, perpendicolare a FT, forma un angolo pari a 60° rispetto
all’orizzontale.
da cui si ricava T  2
3) T2   (f 2 ) 2 
60°
FR
-at
(g- at)
FT
at
60°
g
m
(2 Lf 2 ) 2  3.1 103 N.
L
4) Poiché il processo avviene a pressione e temperatura costante si ha che la variazioni richieste sono
date da :
(T=cost) A  U  TS
m m
(T=cost) A   pV   p

 a v
 pm
 
 920 J
 v
U  A  TS  A  m  - 10080 J
Applicando l’equazione di Clausius- Clapeyron si ottiene:
 v
dp



;
dT
T
 1
1 

T 

 v a 
dT
T

 3.08 10-4 K m2/N
dp  v
60°