La modulazione di frequenza

Firmato digitalmente da
Alessandro Rossini
CN = Rossini Alessandro
Titolo = Ingegnere
Organizzazione = Ordine degli ingegneri
della provincia di Viterbo/80024120562
C = IT
La modulazine
di frequenza
Dott. Ing. Rossini Alessandro
INTRODUZIONE
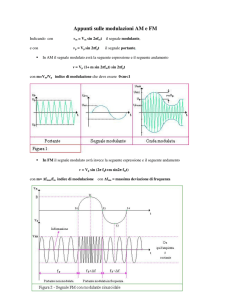
Nelle telecomunicazioni si usano vari tipi di modulazioni. Le modulazioni di portante analogica con
modulante analogica sono tre: modulazione d’ampiezza ( AM ), di fase ( PM ) e di frequenza ( FM ).
Le modulazioni numeriche di portante analogica con modulante digitale più conosciute sono la amplitude
shift keying ( ASK ), la frequency shift keying ( FSK ), la phase shift keying ( PSK ), la binary phase shift
keying ( BPSK ) e la differential phase shift keying ( DPSK ).
Le modulazioni ad impulsi sono modulazioni con modulante analogica di portante digitale dal momento che
si tratta di impulsi. Sono usate la pulse amplitude modulation ( PAM ), la pulse width modulation ( PWM )
o pulse duration modulation ( PDM ) e la pulse position modulation ( PPM ).
A parte viene considerata la pulse code modulation ( PCM ).
In questo documento viene affrontata soltanto la modulazione analogica di frequenza su portante analogica
cosinusoidale. Se l’onda modulante non è sinusoidale o cosinusoidale, con il teorema di Fourier la si può
sempre sviluppare in una serie di armoniche sinusoidali o cosinusoidali.
Nei libri di testo degli istituti tecnici e professionali di solito non si trova la trattazione completa con tutta la
dimostrazione e da questa costatazione è nata l’esigenza d’un opuscolo con una trattazione chiara
dell’argomento con tutti i passaggi.
L’ultimo paragrafo in modo sintetico affronta la modulazione a livello universitario.
2
LA MODULAZIONE DI FREQUENZA
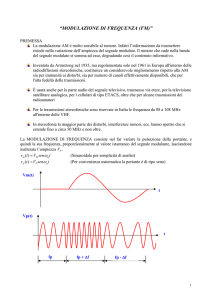
La modulazione di frequenza è un caso particolare della modulazione d’angolo che può essere
analizzata a partire dalla formula delle tensione della portante
vp(t) = Vp cos ϕ ,
dove
Vp è il valore massimo della tensione e
ϕ è l’angolo, funzione del tempo t, che di solito può essere scritto nella forma
ϕ=ωt +θ,
in cui ω rappresenta la pulsazione e θ la fase.
Se varia la pulsazione si tratta d’una modulazione di frequenza ( FM ), se varia la grandezza θ si tratta d’una
modulazione di fase ( PM ), ma la trattazione matematica dei due casi è simile.
La tensione modulante cosinusoidale può essere posta nella forma
vm (t) = Vm cos ( ωm t ) ,
dove
Vm rappresenta l’ampiezza dell’onda modulante e
ωm rappresenta la pulsazione modulante.
Nella modulazione di frequenza si può supporre la fase θ della portante eguale a zero, perché se così non
fosse con una traslazione degli assi la si potrebbe sempre ricondurre a zero e la pulsazione istantanea ω,
variabile nel tempo, conviene che sia definita con la derivata dϕ / dt. In questo caso l’angolo ϕ si può
ottenere con l’operazione di integrazione
t
ϕ = ∫ ω dτ .
0
Se la pulsazione della portante viene modificata con un segnale modulante della forma scritta, si ottiene
ω = ωp + K Vm cos ( ωm t ) ,
dove K è la costante di proporzionalità con cui la modulante modifica la pulsazione della portante.
Calcolando l’angolo ϕ si ottiene
t
∫ [ωp + K Vm cos ( ωm τ ) ] dτ = ωp t + ( K/ωm ) Vm sin ( ωm t ) .
0
L’espressione dell’onda portante modulata diviene
v(t) = Vp cos [ ωp t + ( K/ωm ) Vm sin ( ωm t ) ] .
3
Introducendo l’indice di modulazione m = ( K/ωm ) Vm l’onda portante modulata in frequenza si presenta
nella forma
v(t) = Vp cos [ ωp t + m sin ( ωm t ) ] .
Si può scrivere subito direttamente l’ultima formula, perché si vede immediatamente che si tratta d’una
tensione variabile nel tempo t con ampiezza Vp costante ad andamento cosinusoidale in cui la pulsazione
varia nel tempo. Da questa formula si parte per la dimostrazione vera e propria che consente di arrivare allo
sviluppo in serie di funzioni di Bessel dell’onda modulata in frequenza.
In realtà sotto opportune ipotesi qualsiasi funzione può essere sviluppata in serie di funzioni di Bessel, come
è noto ai matematici, in ogni modo la dimostrazione prevede i passaggi successivi.
Nel caso di modulazione di fase con segnale modulante cosinusoidale l’onda modulata si presenta nella
forma
v(t) = Vp cos [ ωp t + m cos ( ωm t ) ] .
Se l’onda modulante è sinusoidale, la tensione modulata in fase si presenta nella stessa forma del segnale
modulato in frequenza
v(t) = Vp cos [ ωp t + m sin ( ωm t ) ] .
◊
Usando la formula di addizione del coseno, altrimenti nota come corollario del teorema
fondamentale di sottrazione per le funzioni goniometriche,
cos ( α + β ) = cos α cos β - sin α sin β ,
l’espressione dell’onda cosinusoidale modulata in frequenza assume la forma
v(t) = Vp cos ( ωp t ) cos [ m sin ( ωm t ) ] - Vp sin ( ωp t ) sin [ m sin ( ωm t ) ] .
La funzione può essere rappresentata su base ortogonale.
La serie di Fourier in forma rettangolare ( Leon Couch “ Fondamenti di telecomunicazioni “ ) per una
funzione periodica di periodo T0 con ω0 = 2π/Τ0 nell’intervallo compreso tra d e d + T0 può essere scritta
nella forma
∞
∞
s(t) = ∑ an cos ( n ω0 t ) + ∑ bn sin ( n ω0 t ) ,
n=0
n=1
dove i coefficienti hanno le espressioni
d + T0
ao = ( 1 / T0 ) ∫ s(t) dt ,
d
d + T0
an = ( 2 / T0 ) ∫ s(t) cos ( n ω0 t ) dt
d
per n ≥ 1
e
4
d + T0
bn = ( 2 / T0 ) ∫ s(t) sin ( n ω0 t ) dt
d
per n > 0 .
Se una funzione non è periodica, la si può prolungare.
Per le funzioni pari di periodo 2π si ottiene lo sviluppo in serie di Fourier
∞
f(t) = ao/2 + ∑ an cos ( n t )
n=1
con
π
an = ( 2/π ) ∫ f(t) cos ( n t ) dt
0
e per le funzioni dispari
∞
f(t) = ∑ bn sin ( n t ) ,
n=1
con
π
bn = ( 2/π ) ∫ f(t) sin ( n t ) dt .
0
Le formule fornite possono essere tutte dimostrate rigorosamente in campo matematico.
Tornando alla modulazione, il termine cos [m sin ( ωm t ) ] può essere sviluppato in serie di Fourier di soli
coseni ed il termine sin [ m sin ( ωm t ) ] in serie di soli seni.
Applicando lo sviluppo in serie di Fourier al coseno che è una funzione pari si ha
∞
cos [ m sin ( ωm t ) ] = ao/2 + ∑ an cos ( n ωm t )
n=1
dove è
π
an = ( 2 / π ) ∫ cos [ m sin ( ωm t ) ] cos ( n ωm t ) d(ωm t) .
0
Applicando le formule di Werner risulta
π
an = ( 2 / π ) ∫ ( 1 / 2 ) cos [ n ωm t - m sin ( ωm t )] d(ωm t) +
0
5
π
+ ( 2 / π ) ∫ ( 1 / 2 ) cos [ n ωm t + m sin ( ωm t )] d(ωm t)
0
o
π
an = ( 1 / π ) ∫ cos [ n ωm t - m sin ( ωm t )] d(ωm t) +
0
π
+ ( 1 / π ) ∫ cos [ n ωm t + m sin ( ωm t )] d(ωm t) .
0
Le funzioni di Bessel possono essere scritte sotto forma di serie, ma si può dare di esse una rappresentazione
integrale. Le funzioni di Bessel di prima specie ( Gradshteyn e Ryzhyk “ Table of integrals, series and
products “ formula 8. 411,1 ) possono essere scritte nella forma
π
Jn(z) = [1 /( 2π )] ∫ e- inθ + iz sinθ dθ
-π
o
π
Jn(z) = ( 1 / π ) ∫ cos [ n θ - z sin ( θ )] dθ ,
0
dove n è un numero naturale. Con la sostituzione ωm t = θ si può esprimere il coefficiente di Fourier con le
funzioni di Bessel nella forma
π
an = Jn( m ) + ( 1 / π ) ∫ cos [ n ωm t + m sin ( ωm t )] d(ωm t) .
0
Essendo cos ( α ) = cos ( - α ), risulta
π
an = Jn( m ) + ( 1 / π ) ∫ cos [ - n ωm t - m sin ( ωm t )] d(ωm t)
0
e conseguentemente
an = Jn( m ) + J-n( m ) .
Per la proprietà delle funzioni di Bessel di prima specie
J-n( m ) = ( -1 )n Jn( m )
risulta
an = Jn( m ) + ( -1 )n Jn( m ) .
6
Quando n è dispari, il coefficiente di Fourier vale
an = Jn( m ) - Jn( m )
e risulta
an = 0 .
Quando n è pari od eguale a zero è
an = Jn( m ) + Jn( m )
cioè
an = 2 Jn( m ) .
Allora si può scrivere
cos [ m sin ( ωm t ) ] =
∞
J0( m ) + 2 ∑ J2n( m ) cos ( 2n ωm t ) .
n=1
Lo stesso procedimento si può seguire per il seno, che essendo una funzione dispari può essere sviluppato in
serie di Fourier con la formula
∞
sin [ m sin ( ωm t ) ] = ∑ bn sin ( n ωm t ) ,
n=1
dove il coefficiente di Fourier è
π
bn = ( 2 / π ) ∫ sin [ m sin ( ωm t ) ] sin ( n ωm t ) d(ωm t) .
0
Calcolando questo coefficiente con le formule di Werner si ottiene
π
bn = ( 2 / π ) ∫ ( 1 / 2 ) cos [ n ωm t - m sin ( ωm t ) ] d(ωm t) +
0
π
-
( 2 / π ) ∫ ( 1 / 2 ) cos [ n ωm t + m sin ( ωm t ) ] d(ωm t)
0
e conseguentemente in base all’espressione sopra scritta delle funzioni di Bessel
bn = Jn( m ) - J-n( m ) .
Stante la proprietà delle funzioni di Bessel di prima specie
J-n( m ) = ( -1 )n Jn( m ) ,
7
si ottiene
bn = Jn( m ) - ( -1 )n Jn( m ) .
Quando n è pari il coefficiente di Fourier è eguale a zero cioè bn = 0 e quando n è dispari si ottiene
bn = 2 J n ( m ) ,
allora l’espressione del seno è
∞
sin [ m sin ( ωm t ) ] = ∑ 2 J2n+1( m ) sin [ ( 2 n + 1 )ωm t ] ,
n=0
dove 2 n + 1 è il numero dispari.
La tensione di partenza v(t) con una pulsazione delle portante ωp modulata con una funzione di pulsazione
ωm
v(t) = Vp cos ( ωp t ) cos [ m sin ( ωm t ) ] - Vp sin ( ωp t ) sin [ m sin ( ωm t ) ]
assume l’espressione
∞
v(t) = Vp cos ( ωp t ) [ J0( m ) + 2 ∑ J2n( m ) cos ( 2n ωm t ) ] +
n=1
∞
- Vp sin ( ωp t ) { ∑ 2 J2n+1( m ) sin [ ( 2 n + 1 ) ωm t ] } .
n=1
Si applicano nuovamente le formule di Werner e si ottiene
∞
v(t) = Vp J0( m ) cos ( ωp t ) + Vp ∑ J2n( m ) [ cos ( ωp t - 2n ωm t ) + cos ( ωp t + 2n ωm t )] +
n=1
∞
- Vp ∑ J2n+1( m ) { cos [ ( ωp t - ( 2 n + 1 )ωm t ] - cos [ ( ωp t + ( 2 n + 1 )ωm t ] } .
n=0
L’ultima formula si può scrivere in forma compatta usando i valori negativi di n nella sommatoria e si
ottiene
+∞
+∞
v(t) = Vp ∑ J2n( m ) cos ( ωp t + 2n ωm t ) + Vp ∑ J2n+1( m ) { cos [ ( ωp t + ( 2 n + 1 )ωm t ]} .
n=-∞
n=-∞
Il risultato finale è
8
v(t) = Vp
+∞
∑ Jn( m ) cos ( ωp t + n ωm t ) .
n=-∞
◊
In alcuni testi il risultato è scritto per esteso e considerando la terzultima formula della dimostrazione risulta
v(t) = Vp{ J0( m ) cos ( ωp t ) + J2( m ) [ cos ( ωp t - 2 ωm t ) + cos ( ωp t + 2 ωm t )] +
J4( m ) [ cos ( ωp t - 4 ωm t ) + cos ( ωp t + 4 ωm t )] + …} +
-
Vp { J1( m ) [ cos ( ωp t - ωm t ) - cos ( ωp t + ωm t )] +
+ J3( m ) [ cos ( ωp t - 3 ωm t ) - cos ( ωp t + 3 ωm t )] +
+ J5( m ) [ cos ( ωp t - 5 ωm t ) - cos ( ωp t + 5 ωm t )] + …}
o
v(t) = Vp [ J0( m ) cos ( ωp t ) +
- J1( m ) cos ( ωp t - ωm t ) + J1( m ) cos ( ωp t + ωm t ) +
+ J2( m ) cos ( ωp t - 2 ωm t ) + J2( m ) cos ( ωp t + 2 ωm t ) +
- J3( m ) cos ( ωp t - 3 ωm t ) + J3( m ) cos ( ωp t + 3 ωm t ) +
+ J4( m ) cos ( ωp t - 4 ωm t ) + J4( m ) cos ( ωp t + 4 ωm t ) +
- J5( m ) cos ( ωp t - 5 ωm t ) + J5( m ) cos ( ωp t + 5 ωm t ) +
+ ...] .
In questa forma si vede bene lo spettro a righe delle ampiezze del segnale modulato in frequenza. Le
ampiezze del segnale sono proporzionali alle funzioni di Bessel. Alla frequenza della portante
ωp/(2π) l’ampiezza della riga è proporzionale alla funzione di Bessel di prima specie di ordine zero, alle
frequenze ( ωp - ωm )/(2π) e ( ωp + ωm )/(2π) l’ampiezza è proporzionale alla funzione di Bessel di ordine 1,
alle frequenze ( ωp - 2 ωm )/(2π) e ( ωp + 2 ωm )/(2π) l’ampiezza è proporzionale alla funzione di ordine 2,
alle frequenze ( ωp - 3 ωm )/(2π) e ( ωp + 3 ωm )/(2π) alla funzione di ordine 3 eccetera.
9
LE FUNZIONI DI BESSEL
Oltre che nella modulazione di frequenza le funzioni di Bessel si utilizzano in astronomia, in
termodinamica, in meccanica ed in altri campi.
Possono essere di prima specie Jν( x ), di seconda specie Nν( x ), dette di Neumann, e di terza specie Hν( x ),
dette funzioni di Hankel.
L’equazione differenziale del secondo ordine, derivante da quella ipergeometrica,
y ’’ + y ’ /x + ( 1 - ν 2/x2 ) y = 0
ha per soluzioni le funzioni di Bessel.
Quelle di prima specie hanno l’espressione in forma di serie
Jν ( x ) =
xν
∞
x2k
----- Σ ( - 1 )k -----------------------2ν k = 0
22k k! Γ( ν + k + 1 )
con | arg x | < π ;
la funzione Γ( x ) od integrale di Eulero di seconda specie ha l’espressione
∞
Γ( x ) = ∫ e-t t x-1 dt
0
con Re x > 0.
Delle funzioni di Bessel si può dare la rappresentazione integrale usata nella trattazione con l’inviluppo
complesso
+π
Jn(m) = [ 1 /( 2π ) ] ∫ ej ( m sinθ - n θ ) dθ
-π
o quella utilizzata nel precedente paragrafo
π
Jn(m) = ( 1/π ) ∫ cos [ n θ - m sin ( θ ) ] dθ .
0
10
LA TRATTAZIONE CON L’INVILUPPO COMPLESSO
All’espressione con le funzioni di Bessel si può arrivare più rapidamente utilizzando l’inviluppo
complesso del segnale passabanda, però bisogna conoscere
a) la trasformata di Fourier nel dominio della frequenza f d’una funzione del tempo w(t)
+∞
W(f) = ∫ w(t) ej 2π f t dt ,
-∞
b) la funzione delta di Dirac definita come quella funzione δ(x) per cui vale la relazione
+∞
∫ s(x) δ(x) dx = s(0) ,
-∞
dove s(x) è una funzione qualsiasi continua in x = 0,
c) l’espressione generale d’un segnale passabanda
v(t) = Re { g(t) ejωt } ,
dove ω è la pulsazione della portante e g(t) è l’inviluppo complesso, funzione del segnale modulante M(t).
La modulazione di frequenza viene trattata in modo simile alla modulazione di fase. Assumendo
cosinusoidale il segnale modulante
M(t) = A cos ωt
con ω eguale alla pulsazione della modulante, seguendo il procedimento di Leon Couch, l’inviluppo
complesso del segnale modulato è
g(t) = Ac ej β sin(ωωt) ,
dove β è l’indice di modulazione.
Utilizzando la serie di Fourier in forma complessa od esponenziale, risulta
+∞
g(t) = Σ cn ej n
n=-∞
ωt
,
dove i coefficienti sono
T/2
cn = ( Ac / T ) ∫ ej β sin(ωωt) e-j n
-T/2
ωt
dt
cioè
11
+π
cn = Ac (1/2π) ) ∫ ej( β sinθ - n θ ) dθ ,
-π
T è il periodo del segnale modulante e si è fatta la sostituzione ωt = θ.
Tenendo presente la rappresentazione integrale delle funzioni di Bessel, si ottiene
cn = Ac Jn(β) .
Applicando la trasformata di Fourier allo sviluppo in serie di Fourier in forma esponenziale dell’inviluppo
complesso, si ottiene
+∞
G(f) = Σ cn δ( f - n fm )
n=-∞
e conseguentemente
+∞
G(f) = Ac Σ Jn(β) δ( f - n fm ) ,
n=-∞
dove è fm = ω/(2π).
Lo spettro si può calcolare con la formula
S(f) = (1/2) [ G ( f - fc ) + G* ( - f - fc ) ]
dove fc è la frequenza della portante ed l’asterisco indica l’operazione del coniugio.
Con il teorema di Parseval si può calcolare l’energia del segnale.
Nella pratica gran parte della potenza è contenuta nella banda definita dalla regola di Carson
B=2(β+1)b,
dove b è la banda del segnale modulante.
Via Roma 40 Vetralla
2005-08-31
12