P1) Dimostr a che le bisettrici di due angoli coniugati interni, formati

Sulle rette parallele
Angoli coniugati interni e bisettrici
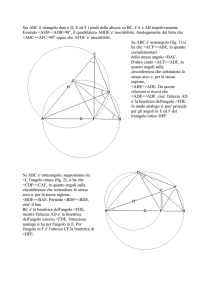
Problema- Dimostrare che le bisettrici di due angoli coniugati interni, formati da due rette parallele
con una trasversale, sono tra loro perpendicolari.
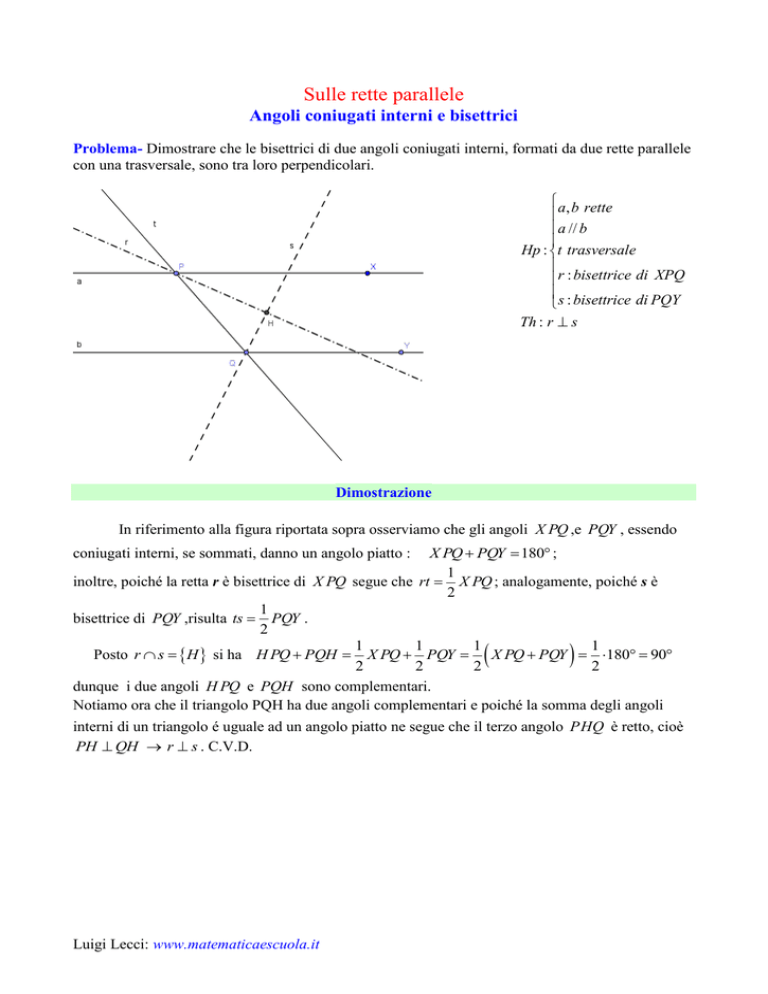
 a, b rette

 a // b

Hp : t trasversale

 r : bisettrice di XPQ
 s : bisettrice di PQY

Th : r  s
Dimostrazione
In riferimento alla figura riportata sopra osserviamo che gli angoli X PQ ,e PQY , essendo
X PQ  PQY  180 ;
1
inoltre, poiché la retta r è bisettrice di X PQ segue che rt  X PQ ; analogamente, poiché s è
2
1
bisettrice di PQY ,risulta ts  PQY .
2
1
1
1
1
Posto r  s  H  si ha H PQ  PQH  X PQ  PQY  X PQ  PQY  180  90
2
2
2
2
dunque i due angoli H PQ e PQH sono complementari.
Notiamo ora che il triangolo PQH ha due angoli complementari e poiché la somma degli angoli
interni di un triangolo é uguale ad un angolo piatto ne segue che il terzo angolo PHQ è retto, cioè
PH  QH  r  s . C.V.D.
coniugati interni, se sommati, danno un angolo piatto :

Luigi Lecci: www.matematicaescuola.it
