Gruppi, Anelli, Campi
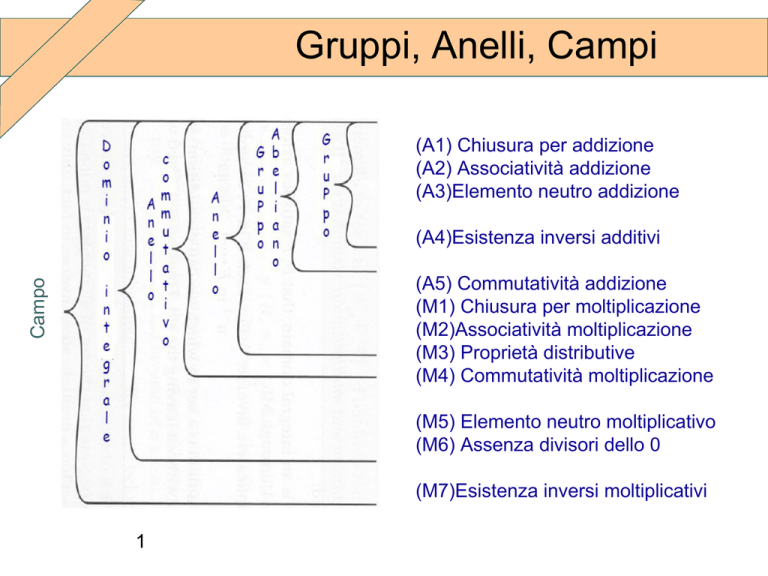
(A1) Chiusura per addizione
(A2) Associatività addizione
(A3)Elemento neutro addizione
(A4)Esistenza inversi additivi
Campo
(A5) Commutatività addizione
(M1) Chiusura per moltiplicazione
(M2)Associatività moltiplicazione
(M3) Proprietà distributive
(M4) Commutatività moltiplicazione
(M5) Elemento neutro moltiplicativo
(M6) Assenza divisori dello 0
(M7)Esistenza inversi moltiplicativi
1
Campi finiti di tipo GF(p)
Un campo finito ( o di Galois) è formato :
Dall’insieme p (con p primo), o dall’insieme q (con q=pn, p
primo e n intero);
da una operazione di “addizione” chiusa, commutativa,
associativa, con elemento identità e con inverso;
da una operazione di “moltiplicazione” chiusa, commutativa,
associativa, distributiva rispetto alla somma, con elemento
identità e in cui ogni elemento ≠0 ha il suo inverso
moltiplicativo o reciproco.
GF(p) e GF(pn) indicano rispettivamente il campo definito su p
e quello definito su q
In GF(p) le operazioni sono quelle dell’aritmetica modulare
2
Campi finiti di tipo GF(p)
Esempio: 2 è il più semplice campo finito:
+
0
1
0
1
0
0
1
0
0
0
1
1
0
1
0
1
(xor)
3
(and)
Example GF(7)
4
Aritmetica polinomiale
Consideriamo polinomi ad una variabile
Possibili diverse alternative
Aritmetica polinomiale ordinaria
Aritmetica polinomiale con aritmetica dei coefficienti mod
p [coefficienti in GF(p)]
Aritmetica polinomiale con coefficienti in GF(p) e
polinomi definiti modulo un polinomio m(x) di grado n
5
Aritmetica polinomiale ordinaria
Include operazioni di somma sottrazione, moltiplicazione
Include anche l’operazione di divisione se la varibile x è un
elemento di un campo
con
6
Aritmetica polinomiale ordinaria
Esempio:
sia f(x) = x3 + x2 + 2 e
g(x) = x2 – x + 1
f(x) + g(x) = x3 + 2x2 – x + 3
f(x) – g(x) = x3 + x + 1
f(x) x g(x) = x5 + 3x2 – 2x + 2
7
Aritmetica polinomiale con coefficienti modulo
Consideriamo polinomi in cui i coefficienti sono elementi di
un campo F
Si parla di polinomi su un campo F
L’insieme di questi polinomi forma un anello polinomiale
Possiamo operare modulo qualsiasi numero primo
Il nostro interesse prevalente è in modulo 2
(In GF(2) addizione equivalente ad XOR e moltiplicazione a
AND)
Siano f(x) = x3 + x2 e
g(x) = x2 + x + 1
allora
f(x) + g(x) = x3 + x + 1
f(x) x g(x) = x5 + x2
8
Divisione polinomiale
Se facciamo aritmetica polinomiale su polinomi su un
campo, allora è possibile la divisione
Questo non vuol dire che sia possibile una divisione esatta
Si può scrivere una divisione polinomiale nella forma:
cioè
r(x) può essere interpretato come il resto r(x) = f (x) mod g(x)
Se non vi è resto si dice che g(x) è divisore di f(x)
Se g(x) non ha altri divisori al di fuori di se stesso ed 1
si dirà che è un polinomio irriducibile o primo
L’aritmetica modulo un polinomio irriducibile forma un campo
9
Aritmetica polinomiale modulare
possiamo definire f(x) mod g(x) = r(x), cioè
f(x) r(x) mod g(x)
se r(x) = 0, diciamo che g(x) divide f(x), e
scriviamo g(x)| f(x)
i polinomi per noi più interessanti sono quelli
a coefficienti in GF(2)
somma e sottrazione coincidono
10
Aritmetica dei polinomi
molti algoritmi crittografici lavorano su interi
compresi tra 0 e 2n-1 (numeri da n bit)
consideriamo gli n bit come i coefficienti in
GF(2) di polinomi di grado n-1
si sceglie un polinomio irriducibile m(x) di grado
m, a coefficienti in GF(2)
Esempio: in AES, le operazioni sui byte vengono
fatte in GF(28), con m(x) = x8 + x4 + x3 + x + 1
scelte diverse per m(x) producono diverse
rappresentazioni di GF(2n), come classe dei
residui modulo m(x)
11
Aritmetica dei polinomi
esempio: per n=3 ci sono solo due polinomi
irriducibili a coefficienti in GF(2):
x3 + x2 + 1
e
x3 + x + 1
Quindi, ci sono due rappresentazioni
diverse (cioè, due etichettature degli
elementi) di GF(23)
per n = 8 ci sono 30 scelte diverse per
m(x)
12
Operazioni in GF(2n)
Fissato il polinomio irriducibile di grado n,
somma: si fa lo xor bit a bit (coefficiente per
coefficiente)
sottrazione: uguale alla somma
prodotto: come per i polinomi ordinari, poi si fa la
riduzione modulo m(x) del risultato
inversione: dato a(x) GF(2n), è possibile
calcolare a-1(x) GF(2n) usando l’algoritmo di
Euclide esteso
divisione: per calcolare a(x)/b(x), si calcola
a(x)b-1(x)
13
Esempio GF(23)
14
Aritmetica polinomiale modulare
Molte operazioni in Rijndael sono definite lavorando sui
singoli byte, c’è quindi la necessità di rappresentare un
byte nel campo finito GF(28).
Un byte b composto dagli 8 bit b7 b6 b5 b4 b3 b2 b1 b0 è
considerato come un polinomio b(x) con coefficienti in
{0,1}:
b7 x7+ b6 x6 + b5 x5 + b4 x4 + b3 x3 + b2 x2 + b1 x + b0
Esempio: il byte con valore in esadecimale ‘57’ (binario
01010111) corrisponde al polinomio
x6 + x4 + x2 + x + 1
15
Aritmetica polinomiale modulare
Somma
Nella rappresentazione polinomiale la somma di due elementi
è un polinomio i cui coefficienti
sono dati dalla somma modulo 2 dei coefficienti dei due
addendi.
Esempio: '57'+'83'='D4' o con la notazione polinomiale:
(x6 + x4 + x2 + x + 1) + (x7 + x + 1) = x7 + x6 + x4 + x2.
In notazione binaria abbiamo: ''01010111'' + ''10000011'' =
''11010100''
Chiaramente l'addizione corrisponde ad un semplice XOR
(denotato con Å) bit a bit.
16
Moltiplicazione
Nella rappresentazione polinomiale, la moltiplicazione in
GF(28) corrisponde ad una
moltiplicazione di polinomi modulo un polinomio binario
irriducibile di grado 8. Un polinomio è
irriducibile se non ha divisori oltre che 1 e se stesso. Per
Rijndael questo polinomio è chiamato m(x) ed è dato da
m(x) = x8 + x4 + x3 + x + 1
o '11B' nella rappresentazione esadecimale.
17
Esempio: '53' · '83' = 'C1' o, nella rappresentazione
polinomiale
(x6 + x4 + x2 + x + 1)(x7 + x + 1) = x13 + x11 + x9 + x8 + x7
+x7 + x5 + x3+ x2 + x
x6 + x 4 + x 2 + x + 1
= x13 + x11 + x9 + x8 + x6 + x5 + x4 + x3 + 1
e facendone modulo m(x) ottengo x7 + x6 + 1 che è il risultato
cercato.
Chiaramente il risultato deve essere un polinomio binario di
grado minore di 8.
La moltiplicazione definita prima è associativa ed ha l’elemento
neutro che è ‘01’ in notazione esadecimale.
18
Per ogni polinomio binario b(x) di grado minore di 8,
l’algoritmo esteso di Euclide può essere usato per calcolare i
polinomi a(x) e c(x) tali che
b(x) a(x) + m(x) c(x) = 1
NOTA: L’algoritmo esteso di Euclide intende trovare il
M.C.D. tra i polinomi b(x) e m(x)
attraverso la tecnica delle divisioni successive.
Percio` a(x)· b(x) mod m(x) =1 oppure b-1(x) = a(x) mod m(x).
19












