Struttura elettronica degli atomi
Modello atomico
di Rutherford
--
+
+
+
---
Incompatibilità con le leggi
classiche dell’elettromagnetismo:
una carica elettrica in moto non
rettilineo ed uniforme perde
progressivamente la propria energia
Insufficienze della fisica classica:
1. Lo spettro del corpo nero
PROBLEMA
Sistemi macroscopici
2. L’effetto fotoelettrico
3. Spettri atomici e molecolari
Sistemi microscopici
Struttura elettronica della materia
1
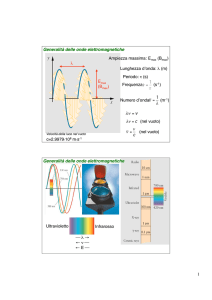
Generalità sulle onde elettromagnetiche
λ
Emax
Ampiezza massima: Emax (Bmax)
Lunghezza d’onda: λ (m)
Periodo: τ (s)
Frequenza: ν =
1
~
ν
=
Numero d’onda:
(m-1)
λ
c
λ = cτ =
ν
1 ν
~
ν= =
λ c
1 -1
(s )
τ
Struttura elettronica della materia
2
Generalità sulle onde elettromagnetiche
Ultravioletto
Infrarosso
⎯λ→
←ν⎯
←E⎯
unità di energia molto usata è eV
= 1.602 10-19Joule
Struttura elettronica della materia
3
Lo spettro del corpo nero
Ogni corpo solido emette radiazioni a spettro continuo. L’intensità della radiazione
emessa dipende da T e l’andamento di I in funzione di λ dipende dalla natura della
sostanza considerata.
Se il corpo emittente è un corpo nero, cioè un corpo che assorbe completamente
la radiazione incidente (cavità a pareti opache con un piccolo foro), lo spettro
emesso risulta indipendente dalla natura della sostanza.
Cavità assimilabile a un
corpo nero
Struttura elettronica della materia
4
Lo spettro del corpo nero
emissione secondo le leggi classiche
curve sperimentali
Secondo le leggi classiche dell’elettromagnetismo l’emissione è
dovuta agli oscillatori elettronici elementari che oscillano con tutte
le frequenze emettendo una radiazione corrispondente, di intensità:
2πκT 2
ν
I=
c2
κ = costante di Boltzmann
Incongruenza con i dati sperimentali
Struttura elettronica della materia
5
Lo spettro del corpo nero
Planck (1899): se si considera che i singoli oscillatori
elementari possano emettere energia di qualsiasi valore, non si
evita la discordanza fra teoria e dati sperimentali.
Si supera, invece, il problema, ammettendo che ogni oscillatore
possa assorbire o emettere solo quantità di energia che sia un
multiplo intero di una quantità minima, detta quanto ε.
ε=hν
h = 6.625·10-34 J s costante di Planck
Nasce la teoria dei quanti.
Struttura elettronica della materia
6
Effetto fotoelettrico
Emissione di elettroni solo per ν >
e--
I
e−
=
1
2
mv max
= Emax = h(ν − ν 0 )
2
num.e−
s ⋅m
νo
2
Emax
∝ I radiazione
La velocità e, quindi, l’energia degli eemessi è indipendente da Iradiazione
νo
ν
In contrasto con
la fisica classica
Struttura elettronica della materia
7
Effetto fotoelettrico - Einstein (Premio Nobel 1921)
fotone
hν hν hν
hν hν hν
Iradiazione ½
hν
e-
hν hν hν
Emax
E = hν > Eo
Ecin = E − Eo = h (ν − νo )
νo
Struttura elettronica della materia
ν
8
Spettro di emissione dell’atomo di idrogeno
Spettro a righe
Analizzatore ottico
Struttura elettronica della materia
9
Spettro di emissione dell’atomo di idrogeno
ν
Serie di Balmer
n=∞
⎛1 1⎞
ν = RH ⎜ − ⎟
⎝ 2 2 n2 ⎠
RH = 109677.76 cm-1
Struttura elettronica della materia
10
Spettro di emissione dell’atomo di idrogeno
ν
1⎞
⎛ 1
− ⎟
ν = RH ⎜
⎝ m2 n2 ⎠
Serie
m = 1, 2, 3, …, ∞
m
Lyman
Balmer
Paschen
Brackett
Pfund
Valida anche per ioni
n = m + 1, …, ∞
n
1
2
3
4
5
2, 3, 4, ...
3, 4, 5, ...
4, 5, 6, ...
5, 6, 7, ...
6, 7, 8, ...
idrogenoidi (He+, Li++, Be+++, …)
Struttura elettronica della materia
11
Il modello atomico di Bohr (Nobel 1922)
r
-
+
Legge di Coulomb
r e2
F = 2
r
(sistema c.g.s.)
r v2
a =
r
e2
r
2
r
r
F = ma
v2
=m
r
E = Ecin + Epot
r =
Accelerazione centripeta
e2
mv
2
2
1
e
= mv 2 −
r
2
No limitazioni su r e E
e2 e2
e2
E=
−
=−
2r
r
2r
Struttura elettronica della materia
12
Il modello atomico di Bohr: primo postulato
Primo postulato
Postulato della quantizzazione della quantità di moto
“il valore del modulo del momento della quantità di moto
dell’elettrone che ruota intorno al nucleo deve essere un multiplo
intero di h/2π”
r ⋅ m ⋅v = n
h
2π
n = 1, 2, …, ∞
r r
r
p = r ∧ mv
r
p = r ⋅ m ⋅ v ⋅ senα
α = 90°
senα = 1
r
p = r ⋅ m ⋅v
r
r
r
v
Struttura elettronica della materia
13
Il modello atomico di Bohr: primo postulato
r ⋅ m ⋅v = n
r =
h
2π
n = ∞ E∞ = 0 eV
n = 4 E4 = -0.85 eV
n = 3 E3 = -1.51 eV
e2
mv 2
n = 2 E2 = -3.4 eV
e2
E= −
2r
En = −
2
h
rn = n 2
4π 2 me2
En = −
n
2
13.6 eV
rn = n 2 ⋅ 0.529 ⋅10 −8 cm
1 2π 2 me4
n2
1
h2
Struttura elettronica della materia
n = 1 E1 = -13.6 eV 14
Il modello atomico di Bohr: primo postulato
∆E = E∞ - E1 = 13.6 eV
Energia di ionizzazione
n = cost
r = cost
E = cost
No emissione
radiazioni e.m.
En = −
Stati stazionari
Stati quantici
1
n
2
13.6 eV
rn = n 2 ⋅ 0.529 ⋅10 −8 cm
r1 = ao = 0.529 ⋅10 −8 cm
Primo raggio di Bohr
Stato
fondamentale
15
Il modello atomico di Bohr: secondo postulato
Secondo postulato
“l’atomo assorbe o emette energia sotto forma di radiazione
elettromagnetica solo quando si verificano dei passaggi
dell’elettrone da uno stato quantico ad un altro: l’energia,
corrispondente alla differenza tra i livelli energetici dei due stati,
viene assorbita o emessa sotto forma di un unico quanto”
Assorbimento
E
Emissione
E
n = n2
E = E2 − E1
hν
E2 − E1
ν=
h
n = n1
n = n2
hν
E = E1 − E2
E1 − E2
ν=
h
n = n1
Struttura elettronica della materia
16
Il modello atomico di Bohr: secondo postulato
Emissione
E A > EB
νA > νB
λA < λB
Struttura elettronica della materia
17
Il modello atomico di Bohr
hν = En ' − En "
En ' − En "
ν=
h
ν En ' − En "
ν = =
c
hc
2
4
1 2π me
En = − 2
n
h2
Legge di Bohr
2π 2 me4 ⎛ 1
1 ⎞
ν =
⎜ 2 − 2⎟
3
h c ⎝n'
n" ⎠
⎛ 1
1⎞
ν = RH ⎜ 2 − 2 ⎟
⎝m
n ⎠
RH = 109677.76 cm-1
Struttura elettronica della materia
18
Il modello atomico di Bohr:
spettri atomici
di emissione
Serie di
Balmer
Serie di
Lyman
19
Critica al modello atomico di Bohr
Introduzione di postulati senza giustificazione
Molte divergenze fra risultati teorici e quelli sperimentali
Ha senso parlare di ORBITE di elettroni intorno al nucleo ?
Moto nel piano x-y di un punto materiale sottoposto ad una forza F
d2x
Fx = m ⋅ ax = m ⋅
dt 2
d2y
Fy = m ⋅ ay = m ⋅
dt 2
Da una doppia integrazione si ottiene: x = x( t )
y = y( t )
y = f ( x ) traiettoria
La doppia integrazione richiede la conoscenza di x0, vx0, y0, vy0.
È necessario conoscere posizione e velocità del punto materiale
in dato istante.
Struttura elettronica della materia
20
Principio di indeterminazione di Heisemberg (Nobel 1932)
È impossibile determinare con precisione contemporaneamente la
posizione e la velocità di una particella di massa molto piccola
Osservazione di un e-:
Incertezza nella determinazione della posizione: ∆x ≅
λ
senθ
Incertezza nella determinazione della velocità: ∆(mv X ) ≅
2h senθ
λ
λ = lunghezza d’onda radiazione usata per illuminare l’eθ = semiapertura angolare della lente usata per l’osservazione
∆x · ∆vx ≅ h /m
∆y · ∆vy ≅ h /m
∆z · ∆ vz ≅ h /m
relazioni di indeterminazione di
Heisemberg
Struttura elettronica della materia
21
Principio di indeterminazione di Heisemberg (Nobel 1932)
Sfera di massa m = 10-5 g
h 6.6 ⋅ 10 −27 erg ⋅ s
−22
2
−1
∆x ⋅ ∆v x ≅
=
=
6.6
⋅
10
cm
⋅
s
m
10 −5 g
∆x = 10 −10 cm
∆v x = 6.6 ⋅ 10 −12 cm ⋅ s −1
incertezza trascurabile
Elettrone m = 10-27 g
h 6.6 ⋅ 10 −27 erg ⋅ s
2
−1
∆x ⋅ ∆v x ≅
=
=
6.6
cm
⋅
s
m
10 −27 g
∆x = 10 −10 cm
∆v x = 6.6 ⋅ 10 10 cm ⋅ s −1
Struttura elettronica della materia
vx indeterminata
22
Dualismo onda-particella
Si possono osservare analogie di comportamento fra fotoni ed
elettroni:
♦i fenomeni di riflessione e di rifrazione per gli e- sono descrivibili
con le leggi classiche della meccanica del punto, per i raggi luminosi
con l’ottica geometrica.
Es: Propagazione in un mezzo a indice di rifrazione costante
Propagazione in uno spazio con campo elettrico nullo
♦i fenomeni di diffrazione e di interferenza per i raggi luminosi sono
descritti attraverso l’ottica ondulatoria, per gli e- fu necessario
introdurre una nuova meccanica
Onde di De Broglie
λDe Broglie →0
h
λ=
mv
fisica macroscopica → meccanica classica
λDe Broglie →10-8cm
fisica atomica → meccanica ondulatoria
Struttura elettronica della materia
23
La meccanica ondulatoria - L’equazione di Schrödinger
Equazione che descrive la propagazione di un’onda:
∂2f ∂2f ∂2f 1 ∂2f
+
+
=
2
2
2
∂x ∂y
∂z
v 2 ∂t 2
f = f(x, y,z,t)
r r
Per esempio per un’onda elettromagnetica, f : E, B
Equazione dell’onda di De Broglie associata ad una particella:
∂ 2ψ ∂ 2ψ ∂ 2ψ 1 ∂ 2ψ
+
+
=
2
2
2
∂x
∂y
∂z
v 2 ∂t 2
ψ = ψ ( x , y ,z ,t )
ψ è detta funzione d’onda
Struttura elettronica della materia
24
La meccanica ondulatoria - L’equazione di Schrödinger
ψ
2
∝ probabilità di trovare la particella in un
dato punto dello spazio in certo istante
Descrizione PROBABILISTICA del moto degli elettroni
∫
V =∞
h
λ=
mv
ψ dV = 1
E = Ecin + E pot = E pot
2
1
+ mv 2
2
λ=
h
v
=
2 m( E − E pot ) ν
∂ 2ψ ∂ 2ψ ∂ 2ψ 1 ∂ 2ψ
+
+
=
∂x 2 ∂y 2 ∂z 2 v 2 ∂t 2
∂ 2ψ ∂ 2ψ ∂ 2ψ
2m
∂ 2ψ
( E − E pot )
+
+
=
∂x 2 ∂y 2 ∂z 2 h 2ν 2
∂t 2
Struttura elettronica della materia
25
L’atomo di idrogeno nella meccanica ondulatoria
Per onde di De Broglie monocromatiche, esprimendo ψ come
funzione sinusoidale del tempo, si ottiene:
Equazione di Schrödinger valida per gli stati stazionari
(indipendenti dal tempo)
∂ 2ψ ∂ 2ψ ∂ 2ψ 8π 2 m
+
+
+
( E − E pot )ψ = 0
2
2
2
2
∂x
∂y
∂z
h
Atomo di idrogeno Epot= - e2/r
∂ 2ψ ∂ 2ψ ∂ 2ψ 8π 2 m ⎛
e2 ⎞
+
E + ⎟ψ = 0
+
+
⎜
∂x 2 ∂y 2 ∂z 2
h2 ⎝
r ⎠
La funzione ψ deve:
• essere nulla all’infinito
• essere continua e ad un solo valore in ogni punto dello spazio,
insieme alle sue derivate
2
∫v =∞ ψ dV = 1
• soddisfare la condizione di normalizzazione
• soddisfare la condizione di ortogonalità
∫v =∞ ψ mψ n dV = 0
Struttura elettronica della materia
26
Risoluzione dell’eq. di Schrödinger per l’atomo di idrogeno
e2 ⎞
∂2ψ ∂2ψ ∂ 2ψ 8πm ⎛
⎜⎜ E + ⎟⎟ ψ = 0
+
+
+
r ⎠
h2 ⎝
∂x 2 ∂y 2 ∂z 2
Integrando:
Soluzioni accettabili solo per determinati valori dell’energia E
(autovalori):
En = −
1 2 π 2 me 4
n2
h2
n = 1,2, 3,..., ∞
Numero quantico principale
coincide con l’espressione dedotta da Bohr!
Quantizzazione dell’energia (livelli energetici discreti):
• non da postulati arbitrariamente imposti (Bohr)
• conseguenza logica della natura dell’equazione e delle
condizioni che la funzione d’onda ψ deve soddisfare per avere
un significato fisico valido
Struttura elettronica della materia
27
Numeri quantici
Le funzioni d’onda ψ soluzioni dell’equazione di Schrödinger
(autofunzioni) sono funzioni matematiche complicate delle
coordinate dello spazio, contengono tre numeri quantici e sono
completamente definite dai loro valori
• Numero quantico principale n : definisce l’energia dell’e• Numero quantico secondario o azimutale l : definisce il
r
h
momento della quantità di moto
p = l ( l + 1) ⋅
2π
• Numero quantico magnetico ml : definisce la proiezione del
momento della quantità di moto sulla direzione z di un campo
magnetico esterno
h
n = 1, 2, 3, ..., ∞
l = 0 ,1, 2, ..., n − 1
m l = −l , − ( l − 1), ..., 0 , + ( l − 1), +l
p z = ml ⋅
Struttura elettronica della materia
2π
28
Numeri quantici e orbitali
Ogni autofunzione associata ad una definita terna di valori
di numeri quantici n, l, ml (ψ n, l, ml ) viene chiamata
ORBITALE.
Ogni orbitale corrisponde ad un determinato stato
quantico possibile dell’elettrone, la cui energia è:
1 2 π 2 me 4
En = − 2
n
h2
Tipi di orbitali
l=0
l=1
l=2
l=3
Orbitale s
Orbitale p
Orbitale d
Orbitale f
Struttura elettronica della materia
29
n = 1, 2, 3, ..., ∞
l = 0 ,1, 2, ..., n − 1
m l = −l , − ( l − 1), ..., 0 , + ( l − 1), +l
Numeri quantici e orbitali
n = 1 l = 0 ml = 0
1 orbitale 1s
n = 2 l = 0 ml = 0
l = 1 ml = 0,±1
1 orbitale 2s
3 orbitali 2p
n = 3 l = 0 ml = 0
l = 1 ml = 0,±1
l = 2 ml = 0,±1,±2
1 orbitale 3s
3 orbitali 3p
5 orbitali 3d
n=4 l=0
l=1
l=2
l=3
1 orbitale 4s
3 orbitali 4p
5 orbitali 4d
7 orbitali 4f
ml = 0
ml = 0,±1
ml = 0,±1,±2
ml = 0,±1,±2,±3
Struttura elettronica della materia
30
Numeri quantici e orbitali
Struttura elettronica della materia
31
Livelli energetici degli orbitali atomici dell’idrogeno
energia
Per l’atomo di idrogeno il valore dell’energia di un dato orbitale
dipende soltanto dal numero quantico principale n.
Orbitali caratterizzati dallo stesso livello energetico (2s-2p, 3s3p-3d, ecc.) sono detti DEGENERI.
4s
3s
4p
3p
2s
2p
4d
3d
4f
Livelli energetici degli orbitali
atomici dell’idrogeno
1s
Struttura elettronica della materia
32
Rappresentazione degli orbitali atomici
ORBITA (meccanica classica)
definita da un’equazione matematica che ne determina
completamente il tipo e la rappresentazione geometrica nello
spazio
ORBITALE (meccanica quantistica)
definita da un’equazione matematica complicata
• la funzione d’onda ψ non ha un significato fisico diretto
• ⏐ψ⏐2 ∝ probabilità di trovare l’elettrone nel punto considerato
Struttura elettronica della materia
33
Rappresentazione degli orbitali atomici
Simmetria sferica dell’atomo:
Ø
coordinate cartesiane ortogonali (x,y,z)
Ø
coordinate polari sferiche (r,θ,ϕ)
z
ϑ
r
y
x
ϕ
Parte angolare: dipendenza dalla direzione
ψ n ,l ,ml (r , ϑ , ϕ ) = Rn ,l (r ) ⋅ Θl ,ml (ϑ ) ⋅ Φml (ϕ )
Parte radiale: dipendenza dalla distanza dal nucleo
Struttura elettronica della materia
34
Espressioni
delle
funzioni
d’onda per
l’atomo di
idrogeno
Struttura elettronica della materia
35
Rappresentazione degli orbitali s dell’atomo di idrogeno
ψ (1s) =
1
1
3 2
0
⋅e
−
r
a0
(π a )
r
−
r
⋅ ( 2 − ) ⋅ e 2a0
ψ (2s) =
1
a0
4(2π a03 ) 2
1
1
ψ dipende solo da r. Il fattore angolare ( 1 ) 2 è una costante
4π
Simmetria sferica
Superficie di equiprobabilità: ⏐ψ⏐2 = cost
Struttura elettronica della materia
∫v ψ
2
dV = 0.95
36
Rappresentazione degli orbitali s dell’atomo di idrogeno
⏐ψ⏐2 ∝ probabilità per unità di volume
y
dr
r
x
z
⏐ψ⏐2 · dV = ⏐ψ⏐2 · 4πr2dr = dP ∝ probabilità nel volume
infinitesimo di guscio sferico compreso fra r e r+dr
dP /dr = funzione di distribuzione della probabilità
Struttura elettronica della materia
37
Rappresentazione degli orbitali s dell’atomo di idrogeno
⏐ψ⏐2 · 4πr2
r = a0 (raggio 1° orbita di Bohr)
• presenza di (n-1) NODI (⏐ψ⏐2=0)
• r→0
dP /dr →0
• r→∞
dP /dr →0
• “massimi in accordo con Bohr”
1s
r ≈ 4a0 (raggio 2° orbita di Bohr)
2s
3s
Struttura elettronica della materia
r
38
Rappresentazione grafica degli orbitali p dell’atomo di idrogeno
Simmetria cilindrica
Piano nodale ⊥ all’asse
2px
2py
Struttura elettronica della materia
2pz
39
Rappresentazione grafica degli orbitali d dell’atomo di idrogeno
Struttura elettronica della materia
40