Capitolo 1 Algebre di Boole

4
prova
5
prova
Capitolo 1
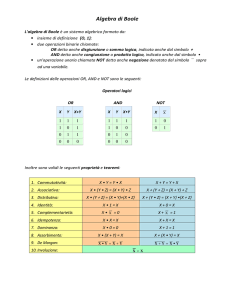
Algebr e di Boole
Definizione 1.1 Una struttura B = (B; ^; _;0 ; 0; 1) è un’algebr a di Boole
se:
(a) B è un insieme non vuoto (detto dom inio dell’algebra) su cui sono definite due operazioni binarie ^ e _, e una operazione unaria 0 ;
(b) B contiene due elementi particolari, indicati con 0 e 1; diver si tr a loro;
(c) per ogni x; y; z 2 B, valgono le seguenti identità:
(commutatività di ^)
(commutatività di _)
(associatività di ^)
(associatività di _)
(distributività di ^ risp. a _)
1a) x ^ y = y ^ x
1b) x _ y = y _ x
2a) (x ^ y ) ^ z = x ^ (y ^ z)
2b) (x _ y) _ z = x _ (y _ z)
3a) x ^ (y _ z) = (x ^ y) _ (x ^ z)
3b) x _ (y ^ z ) = (x _ y) ^ (x _ z)
4a) x _ (x ^ y ) = x
4b) x ^ (x _ y) = x
5a) x _ 0 = x
5b) x ^ 1 = x
6a) x ^ x0 = 0
6b) x _ x0 = 1
(distributività di _ risp. a ^)
(legge di assorbimento)
(legge di assorbimento)
(0 è elemento neutro risp. a _)
(1 è elemento neutro risp. a ^)
Le operazioni ^ e _ sono chiamate rispettivamente infim o (inf ) e supr emo
(sup). Sarà il contesto a chiarire quando i simboli ^ e _ esprimono le operazioni booleane e quando la congiunzione e la disgiunzione logiche. Valendo
per ^ e _ la proprietà associativaV(assiomi
2a e 2b), è possibile estendere
W
V tali
operazioni binarie agli operatori e , dove, per X = fx1 ; :::; xn g,
xi
xi 2X
W
sta per x1 ^ ::: ^ xn e
xi sta per x1 _ ::: _ xn :
xi 2X
Esempio 1.2 Sia U un insieme non vuoto e B un insieme non vuoto di sottinsiemi di U chiuso per \; [ e c: In tal caso ; 2 B e U 2 B: Infatti, per
le proprietà di chiusura, da X 2 B seguono X c 2 B; X \ X c = ; 2 B e
X [ X c = U 2 B. Impiegando la seguente interpretazione:
^
_
0
0
1
Ã
Ã
Ã
Ã
Ã
\
[
c
;
U
8
risulta che tutti gli assiomi (1a)¡(6b) vengono soddisfatti. Pertanto (B ; \; [;0 ; ;; U )
è un’algebra di Boole. Chiamiamo le algebre di Boole di questo tipo algebre
di insiem i (o anche, secondo la terminologia più diffusa, cam pi di insiemi,
pur non essendovi alcun legame significativo con le strutture di campo). La
più grande algebra di insiemi su U è l’insiem e delle par ti di U :
B = P (U ) = fX : X µ U g
Infatti, P (U ) è chiuso per intersezione, unione e complemento. Tale algebra ha
2Card(U) elementi. La più piccola algebra di insiemi su U ha invece 2 elementi
ed ha come dominio
B = f;; U g :
Non esistono campi di insiemi di un elemento, né di due elementi diversi dal
precedente.
E sem pio 1.3 Sia n > 1 un numero primo oppure il prodotto di numeri primi distinti tra loro, e sia B l’insieme dei divisori propri ed impropri di n (ad
esempio, per n = 2 ¢ 3 ¢ 7 = 42 abbiamo B = f1; 2; 3; 7; 6; 14; 21; 42g). Con
l’interpretazione
^
_
x0
0
1
Ã
Ã
Ã
Ã
Ã
M CD
mcm
n
x
1
n
B = (B ; M CD; mcm; n
x ; 1; n) è un’algebra di Boole. Ci limitiamo ad osservare che B è chiuso rispetto alle operazioni di M C D e mcm (infatti, sia il
massimo comun divisore che il minimo comune multiplo di due divisori di n
sono ancora divisori di n), ed anche rispetto all’operazione n
x (se x è un divisore di n anche n
lo
è).
L’
ipotesi
che
n
sia
il
prodotto
di
numeri
primi distinti tra
x
loro serve per verificare l’assioma x ^ x0 = 0 che, tradotto seguendo la tabella
precedente, diviene M C D(x; n
x ) = 1: Infatti, se tale ipotesi non fosse soddisfatta (ad esempio, se considerassimo n = 2 ¢ 2 ¢ 3 = 12) allora, prendendo
x = 2, avremmo 12
2 = 6 e M C D(2; 6) = 2 6= 1:
Definizione 1.4 Siano B1 = (B1; _1; ^1 ;01 ) e B 2 = (B2; _ 2; ^2;02 ) due algebre di Boole. Diciamo che B2 è una sottalgebr a di B1 se:
1) B 2 µ B1;
2) le operazioni _2 ; ^2;02 coincidono rispettivamente con le operazioni _1 ; ^1;01
ristrette a B2,
Dalla definizione si ricava che, se B1 = (B1; _; ^;0 ) è un’algebra di Boole
e B2 µ B 1 allora B 2 è il dominio di una sottalgebra di B1 sse è chiuso per
9
_; ^;0 : Solo in questo caso, infatti, le restrizioni di _; ^;0 a B2 sono a loro
volta operazioni su B2 .
Tra le sottalgebre di un’algebra viene considerata anche l’algebra stessa, detta
sottalgebr a impropr ia. Ogni altra sottalgebra è detto propr ia.
Esempio 1.5 Si consideri l’algebra P (U ), dove U = fa; b; cg (in casi come
questo, indichiamo il solo dominio per denotare l’algebra, e scriviamo P (U )
invece (P (U ); \; [;0 ; ;; U ) ). L’insieme f;; fbg ; fa; cg ; U g è (dominio di)
una sottalgebra di P (U ); è infatti chiuso per intersezione, unione e complemento.
Esempio 1.6 Se U è infinito, allora una particolare sottalgebra di P (U ) è
costituita dall’insieme B di tutti i sottinsiemi finiti e cofiniti di U (un insieme
X µ U è cofinito se X c è un insieme finito). Infatti, B è chiuso per intersezione (l’intersezione di due finiti oppure di un finito e un cofinito è finita,
l’intersezione di due cofiniti è cofinita) e per complemento (il complementare
di un finito è cofinito e viceversa). Questa algebra di insiemi prende il nome
di algebr a dei finiti e cofiniti di U .
1.1
L’algebra di Boole della logica proposizionale.
La logica considera solo proposizioni dichiar ative, quelle cioè di cui ha senso
chiedersi se sono vere o false. D’ora in poi, con il termine proposizione o
enunciato intenderemo sempre una proposizione dichiarativa.
Vero e falso, che indichiamo con 1 e 0, sono i detti valor i di ver ità. Scriveremo
V (®) = 1
e
V (®) = 0
per indicare rispettivamente la verità e la falsità di ®.
I con nettivi
E’possibile combinare tra loro varie proposizioni, al fine di ottenere proposizioni più complesse. Se il valore di verità della proposizione ottenuta dipende
unicamente dai valori di verità delle proposizioni componenti allora si dice che
la combinazione è vero-funzionale. Sono stati isolati cinque modi di combinare in modo vero-funzionale le proposizioni, e sono quelli che si ottengono
mediante le locuzioni ‘‘e ’’, ‘‘o’’, ‘‘non’’, ‘‘se...allora ’’e ‘‘se e solo se ’’. Tali
10
locuzioni, collettivamente, sono chiamate connettivi pr oposizionali e, individualmente, congiunzione, disgiunzione, negazione, im plicazione e doppia
im plicazione. Molto sovente, per comodità , vengono indicate mediante simboli, che non hanno tuttavia raggiunto uno standard universale. La simbologia
che noi impiegheremo è la seguente:
nome
congiunzione
disgiunzione
negazione
implicazione
doppia implicazione
lettura
e
o
non
se...allora
se e solo se
simbolo
^
_
:
!
$
Prendendo come esempio il connettivo ^; la verofunzionalità con cui la logica
lo considera si traduce nel fatto che il valore di verità della formula ® ^ ¯ dipende unicamente dal valore di verità di ® e ¯ ; questa dipendenza è usualmente
espressa tramite una tabella. Nel caso della congiunzione, la tabella mostra che
® ^ ¯ è vera solo quando ® e ¯ sono vere, ed è falsa in ogni altro caso. Allo
stesso modo si leggono le tabelle degli altri connettivi: pertanto, la disgiunzione ® _ ¯ è falsa se entrambi i congiunti sono falsi, ed è vera in ogni altro caso.
L’implicazione ® ! ¯ è falsa se è vero ® ed è falso ¯, ed è vera in ogni altro
caso. La doppia implicazione ® $ ¯ è vera se ® e ¯ hanno lo stesso valore di
verità, falsa altrimenti.
®
0
congiunzione: 0
1
1
®
0
implicazione: 0
1
1
¯
0
1
0
1
¯
0
1
0
1
®^¯
0
0
0
1
®!¯
1
1
0
1
negazione:
®
0
disgiunzione: 0
1
1
®
0
doppia implicazione: 0
1
1
®
0
:®
1
1
0
¯
0
1
0
1
¯
0
1
0
1
®_¯
0
1
1
1
®$ ¯
1
0
0
1
11
For mule ben for mate
In questo paragrafo affrontiamo quello che costituisce il primo problema sintattico di ogni linguaggio formale: la determinazione delle regole per la costruzione delle formule. Nel paragrafo successivo tratteremo invece il corrispondente problema sem antico, consistente nello stabilire il valore di verità
delle formule ottenute.
Poiché, nelle connessioni vero-funzionali, l’unico elemento rilevante di una
proposizione è il suo valore di verità, è possibile ed opportuno rappresentare le
proposizioni con variabili. Formule più complesse si ottengono a partire dalle
variabili mediante l’impiego dei connettivi. Pertanto, l’alfabeto del Linguaggio P roposizionale si limita a:
² un insieme infinito X = fp0; p1; p2; :::g di var iabili pr oposizionali , anche
indicate con p; q; r::: ;
² l’insieme f:; ^; _; !; $g dei connettivi proposizionali;
² le parentesi tonde ( e ), nel ruolo di simboli ausiliari.
L’insieme F P C delle for mule pr oposizionali ben for m ate (o più semplicemente for m ule pr oposizionali, o anche for m ule quando non siano possibili
fraintendimenti) è definito ricorsivamente come segue:
1) per ogni n, pn 2 F P C (a parole: ogni variabile proposizionale è una formula);
2) se ® 2 F PC allora (:®) 2 F PC (a parole: se ® è una formula allora anche
(:®) è una formula);
20 ) se ®; ¯ 2 F PC allora (® ^ ¯); (® _ ¯ ); (® ! ¯); (® $ ¯ ) 2 F P C (a
parole: se ® e ¯ sono formule allora anche è una formula allora anche (® ^
¯ ); (® _ ¯); (® ! ¯) e (® $ ¯) sono formule);
3) nient’altro appartiene a F PC:
Un esempio:
((p ! q) _ ((:p) ^ r)) è una formula. Infatti:
per (1) lo sono p; q; r;
per (2) lo è (:p) ;
per (20) lo sono (p ! q) e ((:p) ^ r);
per (20) lo è ((p ! q) _ ((:p) ^ r)):
Il processo costruttivo può essere evidenziato mediante un diagramma ad albero, che chiameremo albero di costr uzione della for m ula:
12
p
Â
q
j
(p ! q)
Â
Á
p
j
(:p)
j
((:p) ^ r)
r
Á
((p ! q) _ ((:p) ^ r))
Le formule che intervengono nella costruzione di una formula ® vengono dette
sottofor m ule di ®: Convenzionalmente, anche la formula stessa viene considerata una sua sottoformula (così come un insieme è considerato sottinsieme di
se stesso). Quindi, p; q; r; (:p) ; (p ! q) e ((:p) ^ r) sono, oltre alla stessa
((p ! q) _ ((:p) ^ r)); le sottoformule di ((p ! q) _ ((:p) ^ r)): Le sottoformule diverse dalla formula stessa vengono dette sottofor mule pr opr ie.
L’ultimo connettivo impiegato per costruire una formula è definito connettivo
pr incipale, e dà il suo nome alla formula stessa. Una formula è quindi una
congiunzione se il suo connettivo principale è ^; una disgiunzione se il suo
connettivo principale è _, etc..
Vi sono alcune convenzioni che consentono di ridurre, senza creare ambiguità,
il numero di parentesi nella scrittura di una formula. Innanzitutto, le parentesi
esterne possono essere omesse.Inoltre, in assenza di parentesi, la negazione si
intende riferita alla minima sottoformula che la segue. Ad esempio, :p ! q sta
per ((:p) ! q). Volendo invece scrivere :(p ! q) le parentesi non possono
essere omesse.
Ver ità di una for mula
Mediante le tavole di verità dei connettivi è possibile determinare in modo
meccanico il valore di verità di una formula ® a partire da quello delle lettere
proposizionali che la compongono. Come mostrano gli esempi successivi, il
modo più semplice di procedere (non certo il più rapido) consiste (1) nello
scrivere su una stessa riga tutte le sottoformule di ®, facendo in modo che
ogni sottoformula sia successiva alle sue sottoformule e (2) scrivendo sotto le
variabili proposizionali tutti i possibili assegnamenti di verità, attribuendo poi,
per ciascuno di essi, il valore di verità a le varie sottoformule fino a giungere
alla formula finale.
E sem pio 1.7
Tavola di verità della formula p _ : (p ! :p) :
13
p
:p
p ! :p
: (p ! :p)
p _ : (p ! :p)
0
1
1
0
1
0
0
1
0
1
Esempio 1.8
p
q
:q
p!q
:q _ p
p ! q ^ (:q _ p)
0
0
1
1
0
1
0
1
1
0
1
0
1
1
0
1
1
0
1
1
1
0
0
1
Esempio 1.9
p
0
0
0
0
1
1
1
1
q
0
0
1
1
0
0
1
1
r
0
1
0
1
0
1
0
1
Tavola di verità della formula p ! q ^ (:q _ p):
Tavola di verità della formula : ((p ! q) ^ (p _ r)) :
p!q
1
1
1
1
0
0
1
1
p_r
0
1
0
1
1
1
1
1
(p ! q) ^ (p _ r)
0
1
0
1
0
0
1
1
: ((p ! q) ^ (p _ r))
1
0
1
0
1
1
0
0
O sser vazione 1.10 Se una formula ha n variabili proposizionali, i possibili
assegnamenti di verità sono 2n , ed altrettante sono quindi le righe della tavola
di verità. Le colonne sono invece tante quante le sottoformule.
Una tavola di verità può essere costruita senza esibire tutte le sottoformule, ma
scrivendo i valori di verita dapprima sotto tutte le occorrenze delle variabili e
poi, via via, in corrispondenza dei connettivi principali di ciascuna delle sottoformule. In tal modo, la tavola di verità della formula ® è data dalla colonna
che si trova sotto il suo connettivo principale. Ripresentiamo in questo modo
le tavole di verità dei precedenti Esempi 1.7 - 1.9. La colonna sotto il connettivo principale della formula, che indica il valore di verità della formula stessa,
è stata evidenziata.
p
0
1
p
0
1
_
0
1
:
0
1
(p
0
1
!
1
0
:
1
0
p)
0
1
14
p
0
0
1
1
p
0
0
0
0
1
1
1
1
q
0
0
1
1
0
0
1
1
q
0
1
0
1
(p
0
0
1
0
r
0
1
0
1
0
1
0
1
:
1
0
1
0
1
1
0
0
!
1
1
0
1
q)
0
1
0
1
((p
0
0
0
0
1
1
1
1
^
1
0
0
1
!
1
1
1
1
0
0
1
1
(:
1
0
1
0
q)
0
0
1
1
0
0
1
1
q
0
1
0
1
^
0
1
0
1
0
0
1
1
_
1
1
1
1
(p
0
0
0
0
1
1
1
1
p)
0
0
1
1
_
0
1
0
1
1
1
1
1
r))
0
1
0
1
0
1
0
1
Spesso l’esecuzione di una tavola di verità contiene alcuni passaggi inutili, che
possono essere omessi. In molti casi infatti è possibile ricavare il valore di
verità di ® ¤ ¯ (dove ¤ indica un generico connettivo binario) dal solo valore
di verità di ® o dal solo valore di verità di ¯ . Elenchiamo qui di seguito i casi
possibili:
1.
2.
3.
4.
5.
6.
se
se
se
se
se
se
®è
¯è
®è
¯è
®è
¯è
falsa allora ® ^ ¯ è falsa;
falsa allora ® ^ ¯ è falsa;
vera allora ® _ ¯ è vera;
vera allora ® _ ¯ è vera;
falsa allora ® ! ¯ è vera;
vera allora ® ! ¯ è vera.
Dalle 1 ¡ 6 si vede come $ sia l’unico dei quattro connettivi binari introdotti che necessita sempre della conoscenza del valore di verità di entrambe le
formule coinvolte.
Riprendiamo quindi ancora una volta le tre tavole di verità dei precedenti esempi, applicando le regole 1-6 per eliminare alcuni passaggi:
p
0
1
p
0
1
_
0
1
:
0
(p
0
!
1
:
p)
15
Infatti, nel caso in cui p è vero, tutta la formula, che è una disgiunzione, è vera,
per cui è inutile determinare il valore di verità del secondo disgiunto, costituito
dalla sottoformula :(p ! :p):
p
0
0
1
1
p
0
0
0
0
1
1
1
1
q
0
1
0
1
q
0
0
1
1
0
0
1
1
(p
0
1
r
0
1
0
1
0
1
0
1
!
1
q)
0
1
:
1
0
1
0
1
1
0
0
^
1
0
0
1
0
1
(:
1
0
((p
!
q)
0
1
0
1
0
0
1
1
1
0
0
1
1
1
1
q
0
1
^
0
1
0
1
0
0
1
1
(p
0
0
1
1
_
1
0
p))
1
1
0
_
0
1
0
1
r))
0
1
0
1
1
1
Naturalmente, data una formula, esiste il minimo numero di valori di verità da
assegnare (di caselle da riempire) per determinare la sua tavola di verità, ma tale
minimo numero può essere ottenuto in modi diversi; ad esempio, è indifferente
se, per determinare la falsità di una implicazione p ! q; si impiega la falsità
di p o la verità di q: In tal modo, non esiste generalmente la migliore tavola,
ma esistono diverse prime classificate a pari merito.
1.2
Funzioni di ver ità
Considerando la tavola di verità della negazione, osserviamo che essa si comporta come una funzione da f0; 1g a f0; 1g, e precisamente una funzione f tale
che
f (0) = 1
f (1) = 0
2
Ogni connettivo binario si comporta invece come una funzione da f0; 1g a
f0; 1g ; cioè come una funzione in due variabili da f0; 1g a f0; 1g. Ad esempio,
16
la funzione corrispondente alla congiunzione è
f (0; 0) =
f (0; 1) =
f (1; 0) =
f (1; 1) =
0
0
0
1
Così come ad un connettivo binario corrisponde una funzione di verità in due
variabili, alla tavola di verità di una formula ® in n variabili proposizionali
n
corrisponde una funzione f da f0; 1g a f0; 1g, detta appunto funzione di ver ità cor r ispondente ad ®: Tale funzione associa ad ogni n-pla v = (c1; :::; cn)
di 0 ed 1 il valore di verità che la formula assume ponendo, per ogni i · n,
V (pi) = ci , cioè dando ordinatamente i valori c1; :::; cn alle variabili p1; :::pn
di ®:
Ciascuna n-pla v = (c1 ; :::; cn) di 0 ed 1 viene detta valutazione (o n -valutazione
quando occorre specificare il numero delle variabili). Quindi, una funzione di
verità in n variabili è una funzione dall’insieme delle n-valutazioni all’insieme
f0; 1g dei valori di verità.
Ad esempio, la funzione di verità corrispondente alla formula (p ! q) ^ (:q _
p) dell’Esempio 1.8, e che otteniamo dalla sua tavola di verità, è:
f (0; 0) =
f (0; 1) =
f (1; 0) =
f (1; 1) =
1
0
0
1
La funzione di verità f corrispondente alla formula
p _ : (p ! :p)dell’Esempio 1.7 è:
f (0) = 0
f (1) = 1
La funzione di verità corrispondente alla formula : ((p ! q) ^ (p _ r)) dell’Esempio 1.9 è
f (0; 0; 0)
f (0; 0; 1)
f (0; 1; 0)
f (0; 1; 1)
f (1; 0; 0)
f (1; 0; 1)
f (1; 1; 0)
f (1; 1; 1)
=1
=0
=1
=0
=1
=1
=0
=0
17
n
Teor ema 1.11 Le funzioni di verità in n variabili sono 2(2 ) :
Dimostrazione. jf0; 1gj = 2 e quindi jf0; 1gn j = 2n ejff : f : f0; 1gn ! f0; 1ggj =
n
2(2 ).
Alla formula p _ : (p ! :p) corrisponde la stessa funzione di verità della più
semplice formula p; lo stesso accade tra p ! q ^ (:q _ p) e p $ q; a cui
corrisponde di nuovo la stessa funzione di verità. E’quindi possibile che a
formule diverse corrisponda la stessa funzione di verità. Detto in altri termini:
indicando con A l’insieme delle formule ben formate e con B l’insieme delle
funzioni di verità (in qualunque numero di variabili), la funzione F che associa
ad ogni formula la corrispondente funzione di verità non è iniettiva. Sorge
allora la domanda: F è suriettiva? Cioé: data una qualunque funzione di verità,
esiste una formula a cui corrisponde tale funzione? La risposta, positiva, verrà
data nel Teorema 1.23.
1.3
Tautologie e contr addizioni
Definizione 1.12 Una formula è una tautologia se è vera per ogni assegnamento di verità dato alle sue variabili.
In altri termini, una formula è una tautologia se la corrispondente funzione di
verità vale sempre 1.
Esempio 1.13 Le formule :p _ :(p ! :p) e (p ^ q) ! (p _ q) sono tautologie. Infatti la loro funzione di verità vale costantemente 1.
p
0
1
p
0
0
1
1
:
1
q
0
1
0
1
p
0
(p
0
0
_
1
1
^
0
0
0
:
(p
!
:
p)
1
1
0
0
1
q)
0
!
1
1
1
1
(p
_
q)
1
1
18
Altri esempi di tautologie:
p _ :p
: (p ^ :p)
(p ! :p) ! :p
::p $ p
(p ^ q) ! (p ! q)
(p ^ q) ! (p $ q)
(p ! q) _ (q ! p) :
Definizione 1.14 Una formula è una contr addizione se è falsa per ogni assegnamento di verità dato alle sue variabili.
Quindi, una contraddizione è una formula la cui corrispondente funzione di
verità vale sempre 0.
E sem pio 1.15 Le formule p ^ :p e : (p _ q) ^ (p ^ q) sono contraddizioni
(e la prima lo è per antonomasia). Infatti:
p
0
1
p
0
0
1
1
q
0
1
0
1
p
0
^
0
0
(:
(p
_
0
1
1
:
p
0
1
q))
^
0
0
0
0
(p
0
0
^
0
0
0
q)
0
Naturalmente:
² ® è una tautologia se e solo se :® è una contraddizione.
Osserviamo che il fatto di essere una tautologia, e così quello di essere una contraddizione, rappresentano proprietà ‘‘rare’’per le formule; in genere, infatti,
una formula non è né una tautologia né una contraddizione.
Eq uivalenza e implicazion e logica
19
Definizione 1.16 Date due formule ® e ¯; diciamo che ® è logicam ente equivalente a ¯ ; e scriviamo
®´¯
se ® $ ¯ è una tautologia.
Osserviamo che il simbolo ´ non appartiene al linguaggio proposizionale, ma
al metalinguaggio, ed ha valenza semantica. Infatti, ® ´ ¯ significa ‘‘® $ ¯
è sempre vera’’.
Dalle definizioni di equivalenza logica, di tautologia e dalla tavola di verità di
$ segue immediatamente questo fatto:
Teor ema 1.17 Se ® e ¯ hanno lo stesso numero di variabili, allora ® ´ ¯ se
e solo se ad esse corrisponde la stessa funzione di verità.
O sser vazione 1.18 In effetti, poiché la funzione di verità corrispondente ad
una formula ne esprime il suo contenuto logico, avere la stessa tavola di verità significa, per due formule, essere indistinguibili da un punto di vista logico. Tuttavia, il concetto di equivalenza logica è un po’più generale di quello di avere la stessa tavola di verità, in quanto possono essere logicamente equivalenti anche formule che coinvolgono un diverso numero di variabili e che hanno quindi una tavola di verità diversa. Ad esempio, le formule
® 1 = p e ®2 = (p ^ q) _ (p ^ :q), nonostante che la prima sia in una
variabile e la seconda in due variabili, sono logicamente equivalenti. Infatti
p $ (p ^ q) _ (p ^ :q) è una tautologia:
p
0
0
1
1
q
0
1
0
1
p
0
0
1
1
$
1
1
1
1
((p
0
0
^
0
0
q)
1
1
1
_
0
0
1
1
(p
0
0
1
^
0
0
1
:
q))
1
0
D’altro canto, le funzioni corrispondenti alla due formule, cioè
f 1(0) = 0
f 1(1) = 1
f 2(0; 0) =
f 2(0; 1) =
f 2(1; 0) =
f 2(1; 1) =
0
0
1
1
sono diverse, per il fatto che la prima è in una variabile e la seconda in due.
Tuttavia, proprio per l’equivalenza delle formule corrispondenti, la seconda
variabile in f2 non ha alcun ruolo, in quanto il valore assunto dalla funzione
dipende solo dalla prima variabile (lo stesso rapporto, in campo algebrico, sussiste tra la la funzione in una variabile f (x) = 2x e funzione in due variabili
f (x; y) = 2x + y ¡ y).
20
Teor ema 1.19 La relazione ´ su F PC è una relazione di equivalenza.
Dimostr azione. Ovvia.
Definizione 1.20 Date due formule ® e ¯; diciamo che ® im plica logicam ente ¯; e scriviamo
®)¯
se ® ! ¯ è una tautologia.
Da questa definizione e dalla tavola di verità di !; segue che ® ) ¯ se,
ogniqualvolta ® è vera, è vera anche ¯: Come già il simbolo ´; anche il simbolo
) di implicazione logica non appartiene al linguaggio proposizionale ma al
metalinguaggio e, ancora, ha valenza semantica. Infatti, ® ) ¯ significa:
‘‘® ! ¯ è sempre vera’’, così come ® ´ ¯ significa ‘‘® $ ¯ è sempre vera’’.
Naturalmente, da ® ´ ¯ seguono ® ) ¯ e ¯ ) ®:
Ad egua tezza
Le equivalenze
((p ^ q) _ (p ^ r)) ´ (p ^ (q _ r)) e ((p _ q) ^ (p _ r)) ´ (p _ (q ^ r))
esprimono l’associatività di ^ e _: In effetti, ciascuna delle formule p^ (q ^ r)
e (p ^ q) ^ r è vera solo nel caso in cui tutte le variabili siano vere, ed è falsa in
ogni altro caso; dualmente, ciascuna delle formule ((p _ q) _ r) e (p _ (q _ r))
è falsa solo nel caso in cui tutte le variabili siano false, ed è vera in ogni altro
caso. Come sappiamo, l’associatività consente l’abolizione delle parentesi e
quindi, nel nostro caso, possiamo scrivere p ^ q ^ r e p_ q _r senza pericolo di
ambiguità. Tale proprietà può essere generalizzata da 3 ad n formule, per cui
possiamo impiegare la scrittura
n
^
pi
i=1
per esprimere la congiunzione p1 ^ p2 ^ ::: ^ pn; e la scrittura
n
_
pi
i=1
per espimere la disgiunzione p1 _ p2 _ ::: _ pn. I simboli
V
e
W
sono definiti
gr ande congiunzione e gr ande disgiunzione. Da quanto osservato precedentemente segue che:
n
V
pi è vera se e solo se sono veri tutti i congiunti.
i=1
21
n
W
pi è vera se e solo se è vero almeno un disgiunto.
i=1
Definizione 1.21 Dato un numero naturale n, definiamo for m ula n-atom ica
una formula del tipo
pÄ1 ^ ::: ^ pÄn
dove, per ogni i · n; pÄi = pi oppure pÄi = :pi .
Alcuni esempi: p ^ q ^ :r è una formula 3-atomica, :p ^ :q è una formula
2-atomica, e poiché la definizione non esclude il caso n = 1; abbiamo che p e
:p sono formule 1-atomiche.
Poiché una grande congiunzione è vera se e solo se tutti i suoi congiunti sono
veri, otteniamo che:
Lemm a 1.22 L’unica valutazione che rende vera una formula n-atomica pÄ1 ^
::: ^ pÄn è v = (c1; :::; cn) dove, per ogni i · n; ci = 1 se pÄi = pi; e ci = 0 se
pÄi = :pi :
Ad esempio, l’unica valutazione che rende vera p^q^:r è (1; 1; 0); cioè quella
che attribuisce il valore vero a p e q e il valore falso a r. L’unica valutazione
che rende vera :p ^ q ^ :r è (0; 1; 0); cioè quella che attribuisce il valore vero
q e il valore falso a p e r:
Teor ema 1.23 (Teorema di Adeguatezza ). Data una funzione di verità f in n
variabili, esiste una formula ® in n variabili proposizionali avente f come corrispondente funzione di verità.
Dimostrazione. Se f assume costantemente il valore 0; allora ® è una qualunque contraddizione (in n variabili), ad esempio (p1 ^ :p1) ^ p2 ^ ::: ^ pn :
Supponiamo allora che f non valga costantemente 0, e sia X = fv1; :::; v mg
l’insieme delle n-valutazioni v tali che f (v ) = 1: Per ogni j · m sia ¯ j =
pÄ1 ^ pÄ2 ^ ::: ^ pÄn la formula n-atomica tale che pÄi = pi se l’i-esimo componente ci della n-valutazione v j è 1, e pÄi = :pi se ci è 0: Per il Lemma 1.22,
v j è l’unica valutazione che rende vera ¯ j : Poniamo
® = ¯ 1 _ ¯ 2 _ ::: _ ¯ m:
Ricordando che una grande disgiunzione è vera se e solo se è vero almeno uno
dei disgiunti, abbiamo che una n-valutazione v di 0 ed 1 rende vera ® se e solo
se v 2 X . E poiché v 2 X se e solo se f (v ) = 1; otteniamo che f è la funzione
di verità corrispondente ad ®:
Le dimostrazioni come la precedente vengono definite ‘‘costruttive’’. Infatti,
l’esistenza della formula ® corrispondente ad f si ricava costruendo tale formula. Schematizziamo le fasi della costruzione:
22
² se f vale costantemente 0 allora ® = (p1 ^ :p1) ^ p2 ^ ::: ^ pn;
Altrimenti:
² si considerano le sequenze (c1; c2; :::; cn ) tali che f (c1 ; c2; :::; cn) = 1;
² per ognuna delle sequenze (c1 ; c2; :::; cn) del punto precedente si
costruisce la formula n-atomica p~1 ^ p~2 ^ ::: ^ p~n tale che p~i = pi se ci è
1, e p~i = :pi se ci è 0;
² si disgiungono le formule n-atomiche ottenute al punto precedente.
Trovare, impiegando il Teoerma di adeguatezza, una formula a cui corrisponde la seguente funzione in due variabili:
f (0; 0)
f (0; 1)
f (1; 0)
f (1; 1)
=0
=1
=1
=0
Soluzione. Le valutazioni v tali che f (v ) = 1 sono (0; 1) e (1; 0) : Alla prima
corrisponde la formula :p1 ^ p2, alla seconda la formula p1 ^ :p2: La formula
cercata è quindi
® = (:p1 ^ p2) _ (p1 ^ :p2) :
E ser cizio 1.24 Trovare una formula a cui corrisponde la seguente funzione
in tre variabili:
f (0; 0; 0) =
f (0; 0; 1) =
f (0; 1; 0) =
f (0; 1; 1) =
f (1; 0; 0) =
f (1; 0; 1) =
f (1; 1; 0) =
f (1; 1; 1) =
1
0
1
0
1
1
0
0
Soluzione. Le valutazioni a cui f assegna il valore 1 sono (0; 0; 0) ; (0; 1; 0) ; (1; 0; 0)
e (1; 0; 1) ; a cui corrispondono (nell’ordine dato e scrivendo p; q; r al posto
di p1; p2; p3 ) le formule (:p ^ :q ^ :r) ; (:p ^ q ^ :r) ; (p ^ :q ^ :r) e
(p ^ :q ^ r) : Pertanto
® = (:p ^ :q ^ :r) _ (:p ^ q ^ :r) _ (p ^ :q ^ :r) _ (p ^ :q ^ r) :
Definizione 1.25 Un insieme di connettivi mediante i quali siano esprimibili
tutte le funzioni di verità si dice adeguato.
23
Il Teorema di adeguatezza, asserendo che ogni funzione di verità è la tavola di
verità di una formula in ^; _; :, ha come immediata conseguenza questo fatto:
Cor ollar io 1.26
L’insieme f^; _; :g è adeguato.
Tra le funzioni di verità che un insieme adeguato esprime vi sono anche le tavole di verità dei connettivi che non appartengono a tale insieme e che in tal
modo risultano esprimibili a partire da quelli che appartengono all’insieme (un
connettivo binario ¤ è espr im ibile mediante i connettivi ¤1 ,..,¤n se esiste una
formula ® in due variabili p; q che impiega solo i connettivi ¤1; ::; ¤n che sia
logicamente equivalente a (p ¤ q)). Poiché l’insieme f^; _; :g è adeguato, i
connettivi ! e $ devono essere esprimibili mediante ^; _; :: In effetti, la
formula equivalente a p ! q, così come ci viene fornita dal Teorema di Adeguatezza, è (p ^ q) _ (:p ^ q) _ (:p ^ :q), ma si può osservare come la più
semplice :p _ q sia ancora equivalente a (p ! q). La formula equivalente a
p $ q fornita dallo stesso algoritmo è (p ^ q) _ (:p ^ :q), e questa volta non
ammette semplificazioni rilevanti.
L’insieme f^; _; :g è tuttavia addirittura ridondante. Infatti ciascuno dei seguenti insiemi di connettivi è adeguato:f:; ^g e f:; _g . Ciò è una conseguenza immediata delle seguenti equivalenze, dette Leggi di De Mor gan.
(p _ q) ´ :(:p ^ :q)
(p ^ q) ´ :(:p _ :q):
Tuttavia, quando si tratta la logica proposizionale in termini algebrici, è consuetudine riferisi all’insieme f^; _; :g (i cosiddetti connettivi booleani). D’ora
innanzi quindi considereremo l’insieme F P C limitandoci alle formule scritte
impiegando i soli connettivi ^; _; :.
Si consideri la relazione ´ di equivalenza logica sull’insieme FP C. Poiché ´
è una relazione di equivalenza, possiamo considerare, data una formula proposizionale '; la sua classe di equivalenza [']´. Prendiamo l’insieme F di tutte
le classi di equivalenza di formule:
F = f[']´ : ' 2 F P Cg :
(F sarà il dominio della costituenda algebra di Boole). Su F definiamo quindi
¹; _
¹e:
tre operazioni ^
¹ nel modo seguente:
¹ [Ã]´
[']´ ^
¹ [Ã]´
[']´ _
:
¹ [']
=
=
=
[' ^ Ã]´
[' _ Ã]´
[:']´
E’immediato dimostrare che tali operazioni sono ’’ben definite’’, cioè non dipendono dalla scelta delle formule con cui si rappresentano le classi. Consideriamo ora la seguente interpretazione, in cui i simboli ^,_ della colonna
di sinistra rappresentano gli operatori booleani inf e sup, ? la classe di equivalenza delle contraddizioni e > la classe di equivalenza delle tautologie (le
24
contraddizioni sono tutte equivalenti tra loro, e così pure le tautologie):
B
^
_
0
0
1
Ã
Ã
Ã
Ã
Ã
Ã
F
¹
^
¹
_
:
¹
?
>
¹; _
¹; :
F = (F; ^
¹ ; ?; >) è un’algebra di Boole. Tale algebra è infinita; infatti,
per ogni i 6= j, pi non è equivalente a pj e quindi [pi ]´ 6= [pj ]´ :
E sem pio 1.27 Dato n > 1, sia F P Cn l’insieme delle formule proposizionali (scritte in ^; _; :) in al più n variabili. Se definiamo come nell’esempio
¹; _
¹;:
precedente le operazioni ^
¹ ; su
Fn = f[']´ : ' 2 F PCng
¹; _
¹;:
otteniamo che F n = (F n ; ^
¹ ; ?; >) è una algebra di Boole. Tale algebra
è finita, essendo
n
Card (F n ) = 22 :
Infatti due formule in n variabili appartengono alla stessa classe di equivalenza se e solo se ad esse corrisponde la stessa funzione di ver ità in n variabili,
n
n
la quale è una funzione da f0; 1g a f0; 1g. Essendo f0; 1g costituito da 2n
n
sequenze, e potendo a ciascuna di esse associare 0 oppure 1, abbiamo 22 possibili funzioni di verità, e quindi altrettante classi di equivalenza. Naturalmente,
il fatto che l’insieme F n sia finito non deve esser confuso con il fatto che non
solo l’insieme F PCn è infinito, ma anche ciascuna classe [']´ è infinita.
1.4
Prime propr ietà delle algebre di Boole
Teor ema 1.28 Per ogni algebra di Boole B e per ogni x 2 B , valgono le
seguenti proprietà:
1) x ^ x = x;
2) x _ x = x;
3) x00 = x;
4) 00 = 1;
5) 10 = 0;
6) x 6= x0;
7) x ^ 0 = 0;
8) x _ 1 = 1:
25
Dimostrazione.
1) x ^ x = (AB5) x ^ (x _ 0) = (AB4) x:
2) x _ x = (AB5) x _ (x ^ 1) = (AB4) x:
3) x =(AB5) x ^ 1 = (AB6) x ^ (x0 _ x00 ) = (AB3) (x ^ x0 ) _ (x ^ x00) =(AB5)
0 _ (x ^ x00) = (AB2) (x ^ x00 ) _ 0 =(AB5) x ^ x00: Allo stesso modo si
dimostra che x00 = x00 ^ x: Per la commutatività x00 ^ x = x ^ x00 e dunque
dalle uguaglianze precedenti segue x = x00 :
4) 00 = (AB5) 00 _ 0 = (AB6) 1:
5) Analoga a (4).
6) Se x = x0 allora, per la (1), x ^ x0 = x: Ma, per AB6, x ^ x0 = 0; e dunque
x = 0: A questo punto, per (4), x0 = 1: Dall’ipotesi segue dunque 0 = 1.
7) x ^ 0 = (AB1) 0 ^ x = (AB5) 0 ^ (0 _ x) =(AB6) 0:
8) Analoga a (7).
1.5
Sottalgebre e generator i
Come sappiamo, se B1 = (B1 ; _; ^;0 ; 0; 1) è un’algebra di Boole e B2 µ B1
allora B 2 è il dominio di una sottalgebra di B1 sse è chiuso per ^; _;0 : Non
è necessario verificare la chiusura rispetto a tutte le operazioni. Vale infatti il
seguente
² Criterio per la determinazione di una sottalgebra. Se B1 = (B 1; _; ^;0 ; 0; 1)
è un’algebra di Boole e B2 µ B 1 allora B2 è il dominio di una sottalgebra di
B1 sse è chiuso per
(1) una tra le operazioni _ e ^;
(2) l’operazione 0 .
Dimostrazione. Le identità (Leggi di De Morgan) x ^ y = (x0 _ y 0 ) 0 e x _ y =
(x0 ^ y 0) 0 sono vere in ogni algebra di Boole, per cui dalla chiusura per _ e
per 0 segue la chiusura per ^ (e analogamente, dalla chiusura per ^ e 0 segue
quella per _). Si osservi inoltre che le identità x ^ x0 = 0 e x _ x0 = 1 sono
anch’esse vere in ogni algebra di Boole (sono assiomi), per cui se B2 è chiuso
per le operazioni allora contiene 0 e 1.
Teor ema 1.29
me di indici e
Siano B = (B; _; ^;0 ; 0; 1) una algebra di Boole, I un insiefBi = (B i; _ i; ^ i;0i ; 0; 1) : i 2 Ig
un insieme di sottalgebre di B: Sia inoltre
\
B0 =
B i:
i2I
0
0
Allora B0 = (B 0 ; _ 0; ^0 ; 0 ; 0; 1), le cui operazioni _0 ; ^0 ; 0 sono _; ^;0 ; ristrette
26
su B 0 ; è ancora una sottalgebra di B. (Dimostrazione per esercizio).
Definizione 1.30 Siano B una algebra di Boole e Y un sottinsieme di B : La
sottalgebr a gener ata da Y è l’algebra costituita dall’intersezione di tutte le
sottalgebre di B che includono Y (per il teorema precedente questa definizione
è corretta). Tale algebra viene indicata con Y : In simboli:
\
Y =
Bi : Y µ Bi v B
i2I
L’insieme Y viene detto insiem e di gener ator i di Y : Nel caso in cui Y coincida
con l’intera algebra B allora Y viene definito un insieme (o sistema) di gener ator i di B. Ovviamente, ogni algebra B ammette un insieme di generatori:
basta prendere tutti i suoi elementi. Un’algebra si dice finitam ente gener ata
se ammette un insieme finito di generatori. Un insieme Y di generatori di B si
dice ir r iducibile se non contiene un sottinsieme proprio in grado a sua volta
di generare B.
Un’algebra finita ammette sempre un insieme di generatori irriducibile: basta
infatti partire dall’intero dominio B e procedere alla successiva eliminazioni
di quegli elementi che risultino ottenibili a partire dai restanti.
E ser cizio 1.31 Consideriamo l’algebra di insiemi P (U ); dove U = fa; b; cg.
Dire se l’insieme Y = fg 1; g 2; g 3g dove g1 = fag ; g2 = fbg ; g 3 = fcg costituisce un insieme di generatori irriducibile per P (U ).
Soluzione. ; = g 1 \ g2 , mentre ogni elemento di P (U) diverso dal vuoto
si ottiene per unione. Quindi l’insieme fg 1; g 2; g 3g è un insieme di generatori. Tuttavia non è irriducibile; ad esempio, anche fg 1; g 2g genera P (U ):
Infatti (g c1 \ g2c ) = fb; cg \ fa; cg = fcg = g3 e in tal modo abbiamo di
nuovo i tre generatori precedenti. Questa volta, fg 1; g 2g è un insieme di generatori irriducibile, in quanto ogni sottinsieme proprio di fg 1; g 2g non genera
P (U ) ma un sua sottalgebra propria. Infatti , l’algebra generata dal solo g1 è
f;; fag ; fb; cg ; U g e quella generata dal solo g2 è f;; fbg ; fa; cg ; U g.
E ser cizio 1.32 Sia U = fa; b; cg : Trovare la sottalgebra di P (U ) generata
dall’elemento fa; bg :
Soluzione. f;; fa; bg ; fcg ; U g :
E ser cizio 1.33 Sia B un’algebra e b un elemento di B.
(1) Dimostrare che se b è diverso da 0 ed 1 allora fbg = f0; b; b0 ; 1g :
(2) f0g = f1g = f0; 1g
Soluzione. Da b otteniamo b0 (che, v. Th.1.28.6, è diverso da b) e quindi b^b0 =
0 e b _ b0 = 1: Inoltre f0; b; b0 ; 1g è chiuso per le tre operazioni.mpi, ... .
27
Definizione 1.34 Definiamo l’insieme TB dei ter m ini booleani (o espressioni booleane). Sia V ar = fx1 ; x2; :::g un insieme infinito di variabili. Allora:
1) V ar µ T B;
³ 0´
2) se ® 2 TB allora ® 2 T B;
20 ) se ®; ¯ 2 TB allora (® ^ ¯ ) 2 TB;
200 ) se ®; ¯ 2 T B allora (® _ ¯ ) 2 TB ;
3) nient’altro appartiene a TB:
Un termine ® nelle variabili x1; :::; xn può essere indicato con ® (x1; :::xn ).
Non è richiesto che in ® compaiano tutte le variabili x1; :::; xn , ma semplicemente che non ne compaiano altre.
Sia ® un termine in x1; :::xn e siano b1; :::; bn elementi di un’algebra di Boole
B. Con
® [b1; :::; bn ]
indichiamo l’elemento di B che otteniamo interpretando, in ®, i generici simboli ^; _;0 nelle corrispondenti operazioni su B e, per ogni i · n, la variabile
xi con l’elemento bi :
0
Esempio 1.35 Sia ® = (x1 _ x2 ) ^ (x1), sia B = (P (U ); \; [;0 ) con U =
fa; b; c; d; eg e siano b1 = fa; cg ; b2 = fa; b; dg : Allora
® [b1; b2 ] = ® [fa; cg ; fa; b; dg] = (fa; cg [ fa; b; dg) \ (fa; cgc) = fb; dg :
Definizione 1.36 Data un’algebra B e due termini ®(x1 ; :::xn ) e ¯(x1; :::xn ),
diciamo che l’identità ® = ¯ è ver a in B se per ogni b1 ; :::; bn 2 B; ® [b1; :::; bn ] =
¯ [b1; :::; bn]. Una identità è valida se è vera in ogni algebra di Boole.
O sser vazione 1.37 La definizione di termine, così come la definizione di verità e di validità, è applicabile (con ovvie modifiche) a tutti i tipi di strutture.
Ad esempio, l’insieme TG dei termini per la teoria dei gr uppi è definito come
segue:
1) V ar µ T G;
2) se ®; ¯ 2 T G allora
¡ (® ¤¢ ¯) 2 TG ;
20 ) se ® 2 TG allora ® ¡1 2 TG;
3) nient’altro appartiene a TG:
Nel caso degli anelli, abbiamo che l’insieme TR dei termini per la teor ia degli
anelli è definito come segue:
28
1) V ar µ TR;
2) se ®; ¯ 2 TR allora (® + ¯ ) 2 TR;
20 ) se ® 2 TG allora (¡®) 2 TR;
2000 ) se ®; ¯ 2 TR allora (® ¢ ¯) 2 TR;
3) nient’altro appartiene a TR:
Anche il seguente teorema, con ovvie modifiche, vale per tutti i tipi di strutture.
Lo enunciamo nella sua generalità:
Teor ema 1.38 Sia B una struttura algebrica (algebra di Boole, gruppo, anello,
...) e Y µ B: Allora
Y = f® [g1; :::; g n] : ® 2 T X e g 1; ::; g n 2 Y g
(1.1)
dove TX è l’insieme dei termini della teoria cui la struttura appartiene.
Dimostr azione. Sia Z = f® [g 1; :::; g n] : ® 2 T X e g 1; ::; gn 2 Y g : Vale Y µ
Z µ Y : Infatti Y µ Z segue dal fatto che Y è ottenibile interpretando in tutti
i modi possibili il termine x: Ma vale anche Z µ Y , in quanto una qualunque
sottostruttura contenente Y , dovendo essere chiusa per le operazioni, dovrà
contenere tutti i termini interpretati in Y e quindi includere Z: Non ci resta che
dimostrare che Z è un sottostruttura, ma questo deriva dall’ovvia chiusura di
Z per le operazioni.
Il riferimento a tutti i termini rende il precedente risultato poco interessante (la
facilità con cui è stato dimostrato ne è un indizio!). Si cerca quindi di identificare un sottinsieme ’’ragionevolmente piccolo’’dell’insieme dei termini che
sia sufficiente a generare la sottostruttura. Questo tipo di risultati sono detti
teoremi di for ma normale e, questa volta, variano da teoria a teoria. Nel caso dei gruppi, ad esempio, si è dimostrato che un tale sottinsieme è costituito
dai termini della forma xÄ1 ¤ ::: ¤ Äxn dove xÄi è xi oppure x¡1
i : Non è quindi
necessario riferirsi a tutti i termini ® ma solo a quelli avente quella particolare forma. Risultati analoghi abbiamo incontrato per gli ideali principali o per
gli ampliamenti algebrici. Nel caso delle Algebre di Boole abbiamo un buon
teorema di forma normale.
Definizione 1.39 Un termine booleano ®(x1; :::; xn ) è detto congiunzione
elem entar e se ha la forma
n
^
x~i
i=1
dove, per ogni i · n, x~i = xi oppure x~i = x0i : Un termine è detto in for m a nor m ale disgiuntiva se è una disgiunzione di congiunzioni elementari .
Indichiamo con F N D l’insieme dei termini in forma normale disgiuntiva.
29
Teor ema 1.40 (Teorema di forma normale per le Algebre di Boole) Sia B
un’algebra e Y µ B: Allora
Y = f® [g1 ; :::; gn ] : ® 2 F ND e g 1; ::; g n 2 Y g :
Dimostrazione. (Cenno. La dimostrazione rigorosa è per induzione). Una termine in F N D è caratterizzato dal fatto che, partendo dalle variabili, prima
interviene (eventualmente) l’operazione di complemento (mai due volte consecutive); poi interviene (eventualmente) l’operazione di inf e infine (eventualmente) quella di sup. Se ® non rispetta questo ordine è possibile ricondursi ad
un termine ¯ che rispetta tale ordine, applicando le seguenti identità, le quali
sono valide e quindi vere in ogni algebra di Boole:
(x ^ y)0 = x0 _ y 0 (da ’’prima ^ poi 0 ’’a ’’prima 0 poi _ ’’.
(x _ y)0 = x0 ^ y 0 (d ’’prima _ poi 0 ’’a ’’prima 0 poi ^ ’’.
(x ^ (y _ z)) = (x ^ y ) _ (x ^ z) (da ’’prima _ poi ^’’ a ’’prima ^ poi
_ ’’.
((y _ z) ^ x) = (x ^ y) _ (x ^ z )
x00 = x: (da ’’due negazioni consecutive’’a ’’nessuna negazione’’.
Vedremo più avanti come, nel caso in cui Y sia finito, sia possibile un ulteriore
miglioramento del risultato di forma normale. Rimandiamo gli esempi a quella
sede.
Dua lità
Dato un termine ®; il termine che si ottiene sostituendo _ con ^ e ^ con _ si
definisce duale di ®: Ad esempio, il duale del termine (x_y )0 ^x è (x^y )0 _x.
Il seguente teorema esprime una caratteristica molto particolare della teoria
delle algebre di Boole.
Teor ema 1.41 (P rincipio di dualità ). Siano ® e ¯ due termini e ® d e ¯ d i
rispettivi duali. L’identità ® = ¯ è valida se e solo se ® d = ¯ d è valida.
Non dimostriamo questo risultato, che comunque segue dal fatto che gli assiomi sono stati dati in modo tale che se ® è un assioma anche ® d è un assioma.
O sser vazione 1.42 Il teorema non asserisce: ‘‘per ogni interpretazione I ;
®[I] = ¯[I] se e solo se ® d [I ] = ¯ d[I]’’bensì: ‘‘per ogni interpretazione I ;
®[I] = ¯[I] se e solo se, per ogni interpretazione I; ® d[I] = ¯ d [I ]’’. In modo
un po’più simbolico, non asserisce
³
´
8I ®[I] = ¯ [I] $ ® d [I ] = ¯ d [I]
30
bensì
³
´
8I(®[I] = ¯ [I]) $ 8I ® d[I] = ¯ d [I] :
Può quindi capitare che, secondo una certa interpretazione I, ®[I] = ¯[I] e
® d [I] 6= ¯ d[I], o viceversa. Un esempio banale: interpretando x1 e x2 con due
elementi b1 e b2 di un’algebra di insiemi tali che b1 ½ b2, l’identità x1 \ x2 =
x1 è soddisfatta, ma non lo è l’identità tra i duali x1 [ x2 = x1 :
1.6
Or dine
Sia B un’algebra di Boole. Definiamo su B una relazione binaria, che indichiamo con il simbolo ·, in questo modo:
x · y se x ^ y = x:
(1.2)
Nel successivo Teorema 1.46 dimostriamo che · è una relazione d’ordine. Prima però vogliamo vedere a cosa corrisponde la relazione · nelle algebre di
Boole fino ad ora incontrate:
E sem pio 1.43 Se B è un’algebra di insiemi allora · è la relazione µ : Infatti
x µ y se e solo se x \ y = x:
E sem pio 1.44 Se B è F oppure F n allora, per la (1.2), [']´ · [Ã]´ se e solo
¹ [Ã]´ = [']´, se e solo se [' ^ Ã]´ = [']´, se e solo se ' ^ Ã ´ ',
se [']´ ^
se e solo se non accade che ' sia vero e à sia falso, se e solo se ' ! à è una
tautologia, cioè sse ' ) Ã. Dalla precedente catena di equivalenze si ottiene
dunque che:
[']´ · [Ã]´ se e solo se ' ) Ã.
(1.3)
E sem pio 1.45 Se B è l’algebra dei divisori di un numero n prodotto di fattori
primi diversi tra loro (v. Esempio ??) allora
x · y se e solo se x è un divisore di y:
Teor ema 1.46
ti proprietà:
Sia B un’algebra di Boole. La relazione · su B ha le seguen-
1) è una relazione d’ordine;
2) per ogni x 2 B , 0 · x · 1;
3) per ogni x; y 2 B, x · y se e solo se x _ y = y;
4) per ogni x; y 2 B, x · y se e solo se x ^ y 0 = 0;
31
5) per ogni x; y 2 B, x ^ y · x · x _ y ;
6) per ogni x; y ; z 2 B, x · y e x · z se e solo se x · y ^ z :
7) per ogni x; y ; z 2 B, x · z e y · z se e solo se x _ y · z:
Dimostrazione. Prima di tutto vogliamo osservare che, qualora B sia un’algebra di insiemi e quindi · corrisponda alla relazione di inclusione, tutte le
precedenti proprietà sono ovvie. Tuttavia la relazione · non si riferisce a priori ad alcun contesto particolare. Le uniche proprietà a cui possiamo appellarci
sono quindi gli assiomi della teoria. Anche la dimostrazione dell’enunciato più
semplice può in tal modo risultare laboriosa. Ci limitiamo a dimostrare (1)-(4).
(1) Proviamo dapprima che · è riflessiva. Per definizione, x · x equivale a
x ^ x = x; che abbiamo dimostrato (Teorema 1.28 (1)). Per dimostrare la
proprietà antisimmetrica supponiamo x · y e y · x: Pertanto x ^ y = x e
y ^ x = y : Per l’assioma AB2, x ^ y = y ^ x e quindi x = y : Infine, per dimostrare la proprietà transitiva, supponiamo x · y e y · z; cioè x ^ y = x e
y ^ z = y : Allora x ^ z = (x ^ y) ^ z = (AB2) x ^ (y ^ z) = x ^ y = x; da
cui segue x · z.
(2) 0 · x significa x ^ 0 = 0, che abbiamo dimostrato in Teorema 1.28. x · 1
significa x ^ 1 = x, cioè AB5:
(3) Supponiamo x · y , i.e.x ^ y = x: Allora x _ y = (x ^ y ) _ y = AB3
(x _ y) ^ (y _ y) =per Teorema1.28 (2) (x _ y ) ^ y = AB1 y ^ (x _ y) = AB4 y :
Il viceversa è analogo.
(4) Se x · y, i.e.x ^y = x; allora x ^y 0 = (x^y )^y 0 = AB2 x^(y ^y 0 ) = AB6
x ^ 0 = 0 (l’ultima identità è stata dimostrata in Teorema 1.28 (7). Pertanto
x · y implica x ^ y 0 = 0: Viceversa, se x ^ y 0 = 0 allora x = AB5 x _ 0 = AB6
x _ (y ^ y 0 ) = AB3 (x ^ y) _ (x ^ y 0 ) = (x ^ y) _ 0 =AB5 x ^ y:
1.7
Atomi
Definizione 1.47 Sia B un’algebra di Boole. Un elemento a 6= 0 appartenente a B è un atomo di B se, per ogni x 2 B, da x · a segue che x = a
oppure x = 0:
Indichiamo con At(B) l’insieme degli atomi di B e, per ogni x 2 B; poniamo
at(x) = fa 2 At(B) : a · xg :
(In tal modo, at è una funzione da B a P (At(B)); si può dimostrare che se B
è finita allora at è biettiva). Chiaramente, se a 2 At(B) allora at(a) = fag,
mentre, per il Teorema 1.46.2, at(0) = ; e at(1) = At(B):
Definizione 1.48 Un’algebra di Boole B è atom ica se ogni elemento non
nullo è un atomo oppure sta sopra un atomo (i.e., se per ogni elemento x 2 B
32
e x 6= 0 abbiamo at(x) 6= ;).
E ser cizio 1.49 Dimostrare che, per ogni insieme U , l’algebra P (U ) è atomica.
Soluzione. At(P (U )) = ffxg : x 2 U g e, per ogni X 2 P (U ), at(X ) =
ffxg : x 2 X g : In tal modo, se X 6= ; allora at(X ) 6= ;:
E ser cizio 1.50 Data un’algebra di Boole B1 sottalgebra di B2, dire se è vero
o falso che At(B 1) µ At(B2 ):
Soluzione. Falso. L’insieme degli atomi di B1 non coincide con l’insieme degli
atomi di B2 contenuti in B1 . Infatti, mentre ogni atomo di B2 contenuto in B1 è
anche atomo di B1, un elemento x che non è atomo di B2 può esser atomo di B 1:
Poniamo, ad esempio, B1 = f;; fa; bg ; fcg ; fa; b; cgg e B 2 = P (fa; b; cg):
B1 è sottalgebra di B2, fa; bg è un atomo di B1 ma non di B2.
Teor ema 1.51 L’algebra F è priva di atomi.
Dimostr azione. Sia [']´ 6= [?]´ : Sia ' in n variabili. Poiché ' non è una
contraddizione, esiste una n-valutazione v delle n variabili che rende vera ':
Sia à = ' ^ pn+1; dove pn+1 non compare in ': La formula à non è una
contraddizione; infatti la n + 1-valutazione v 0 che coincide con v sulle prime n
variabili e che rende vera pn+1 rende vera Ã: In tal modo [?]´ 6= [Ã]´ : Inoltre
à ! ' è una tautologia (ovviamente) mentre ' ! à non è una tautologia;
basta infatti considerare la n + 1-valutazione v 00 che coincide con v sulle prime
n variabili e che rende falsa pn+1. Pertanto [Ã]´ < [']´, e quindi [']´ non è
un atomo.
Teor ema 1.52 Sia ['] n un elemento dell’algebra F n delle classi di equiva´
lenza delle formule proposizionali in n variabili.
n
[']´ è un atomo di F n se e solo se ' è equivalente a una n-congiunzione elementare
(1.4)
cioè se ' ´ p~1 ^ ::: ^ p~n; dove, per ogni i, p~i = pi oppure p~i = :pi
Dimostr azione. Supponiamo che ' sia una n-congiunzione elementare e [Ã]´
n ·
[']´
n : Allora à ! ' è una tautologia, cioè ogni valutazione v delle n variabili che soddisfa à deve soddisfare anche ': Ma '; essendo una congiunzione
elementare, è soddisfatta da una sola valutazione, e precisamente dalla valutazione v tale che
v(pi) =
0 se p~i = :pi
1 se p~i = pi:
Pertanto o à è soddisfatta dalla stessa valutazione e da nessun’altra, o à non è
soddisfatta da alcuna valutazione. Nel primo caso à $ ' è una tautologia e
n = ['] n ; nel secondo caso à è una contraddizione e quindi [Ã] n =
quindi [Ã]´
´
´
n = 0: Da ciò segue che ['] n è un atomo. La dimostrazione inversa è
[?]´
´
analoga.
33
Teor ema 1.53 F n è atomica.
Dimostrazione. Se [Ã] n 6= [?] n allora esiste una valutazione v che soddisfa
´
´
Ã. La congiunzione elementare ' = p~1 ^ ::: ^ p~n tale che
¿
:pi se v(pi) = 0
p~i =
pi se v(pi) = 1
è soddisfatta solo da v: Quindi ' ! Ã è una tautologia e [']´
n · [Ã] n .
´
Come esempio particolare, consideriamo l’algebra F 3 delle classi di equivalenza delle formule proposizionali in 3 variabili, che indicheremo con p; q; r.
L’insieme At(F 3) è costituito dalle 23 = 8 classi di equivalenza delle congiunzioni elementari:
8
9
3
3
3
< [:p ^ :q ^ :r]´ ; [:p ^ :q ^ r]´ ; [:p ^ q ^ :r]´ ; =
3
3
3
At(F 3) =
[:p ^ q ^ r]´ ; [p ^ :q ^ :r]´ ; [p ^ :q ^ r]´ ;
:
;
3
3
[p ^ q ^ :r]´ ; [p ^ q ^ r]´
Teor ema 1.54 Ogni algebra di Boole finita B è atomica.
Dimostrazione. Se un’algebra B non è atomica allora esiste un elemento x 6= 0
per il quale non esiste alcun atomo y tale che y · x. Pertanto neppure x è un
atomo ed esiste un elemento x1 diverso da x e da 0 tale che x1 < x: Ma, per
ipotesi, neanche x1 è un atomo e quindi esiste un elemento x2 diverso da x1
e da 0 tale che x2 < x1: In questo modo si verifica l’esistenza di una catena
discendente infinita di elementi di B
::: < xn < ::: < x3 < x2 < x1 < x
ciascuno differente dall’elemento che lo precede e quindi, essendo < una relazione di ordine stretto, tutti diversi tra loro. Ma ciò è in contrasto con la
finitezza di B.
Teor ema 1.55 Sia B un’algebra di Boole finita (e quindi, per il Teorema 1.54,
atomica). Allora:
W
1) Ogni elemento b di B è supremo di atomi (ponendo a= 0), più precisaa2;
mente,
b=
_
a
a2at(b)
.
2) B ha 2n elementi, dove n è il numero dei suoi atomi.
Cor ollar io 1.56 Per ogni numero naturale m, esiste un’algebra di Boole di
m elementi se e solo se m è una potenza di 2 (con esponente maggiore di 0, non
essendovi, a causa dell’assioma 0 6= 1, algebre di Boole di un solo elemento).
Dimostrazione. Se m non è una potenza di 2 allora, per i Teoremi 1.54 e 1.55.2,
34
non esiste un’algebra con m elementi. Viceversa se m = 2n allora, preso un
insieme U di n elementi, l’algebra di insiemi P (U ) ha m elementi.
Il teorema successivo è l’inverso del precedente Teorema 1.55 (2). Non solo
infatti ogni sottalgebra di un’algebra di 2n elementi ha 2k elementi, con k · n,
ma ...
Teor ema 1.57 Sia B un’algebra di Boole di cardinalità 2n. Per ogni 1 · k ·
n; B ha almeno una sottalgebra C di 2k elementi.
E ser cizio 1.58 Sia U = fa; b; cg : Determinare il numero delle sottalgebre
di P (U ).
Soluzione. Per il Teorema 1.55 (2), tutte le algebre, e quindi tutte le sottalgebre,
hanno come cardinale una potenza di 2 (con esponente maggiore di 0). Poiché
C ard(P (U )) = 8, le sue sottalgebre possono avere 21 = 2, 22 = 4 o 23 = 8
elementi. L’unica sottalgebra di 8 elementi è, ovviamente, P (U ) stessa. L’unica sottalgebra di 2 elementi è f;; U g : Determiniamo dunque il numero delle
sottalgebre di 4 elementi. Come visto nel precedente Esercizio 1.33, ogni elemento X di P (U ) che sia diverso da ; e U genera la sottalgebra di 4 elementi
f;; X; X c; U g e, per l’unicità del complementare, gli unici elementi di P (U )
che generano tale sottalgebra sono X e X c : Poiché vi sono 6 elementi diversi
da ; e U , avremo 62 = 3 sottalgebre di 4 elementi. Il numero delle sottalgebre
di P (U ) è quindi 1 + 3 + 1 = 5:
E ser cizio 1.59 Sia U = fa; b; cg : Trovare tutti i possibili insiemi irriducibili
di generatori di P (U ).
Soluzione. P (U ) non può essere generata da un singolo elemento perché in tal
caso, come visto nel precedente Esercizio 1.33, avrebbe 2 o 4 elementi. Quindi,
i generatori devono essere almeno due. Qualunque sia X µ U , le coppie
fX; X cg, fX; ;g o fX; U g non costituiscono insiemi di generatori per P (U ),
in quanto ciascuna coppia è riducibile a fX g e un solo elemento non è in grado
di generare P (U ). Mostriamo invece che tutte le altre coppie fX; Y g sono in
grado di generarlo. Caso 1. X e Y sono due atomi (ad esempio X = fag
c
e Y = fbg). Allora (X [ Y ) c è il terzo atomo (ad esempio (fag [ fbg) =
c
fa; bg = fcg ) e, disponendo dei tre atomi, si ottiene, per il Teorema 1.55.1,
ogni altro elemento di P (U ): Caso 2. X è un atomo e Y è un insieme di due
elementi e X µ Y (ad esempio X = fag e Y = fa; bg). In tal modo (Y \ X c)
c
è un secondo atomo, cioè un secondo singoletto (ad esempio, fa; bg \ fag =
fa; bg \ fb; cg = fbg) e ci riconduciamo al Caso 1. Caso 3. X e Y hanno
ciascuno due elementi (ad esempio X = fa; bg e Y = fa; cg). In questo caso,
essendo X 6= Y e C ard(U ) = 3, X \ Y è un atomo e ci riconduciamo al
Caso 2. Non vi sono altre coppie possibili di generatori. Inoltre, non vi sono
terne irriducibili di generatori, in quanto ogni terna di insiemi distinti tra loro
e diversi da ; e U contiene almeno una coppia tra quelle considerate nei casi
1-3. A questo
irriducibili
¡ ¢ punto contiamo quanti sono gli insiemi di generatori
¡ ¢
trovati: 32 = 3 nel Caso 1, prendendo 2 dei 3 atomi. 32 ¢ 2 = 6 nel Caso
35
¡ ¢
2. Infatti abbiamo 32 insiemi di 2 elementi, e per ciascuno possiamo scegliere
¡ ¢
2 sottinsiemi di un elemento. Nel Caso 3, abbiamo 32 = 3 possibilità di
scegliere il primo insieme di due elementi e 3 ¡ 1 = 2 possibilità per scegliere
il secondo, ma tale numero 3 ¢ 2 = 6 deve esser diviso per 2! = 2 dal momento
che non conta l’ordine. Gli insiemi di generatori irriducibili sono dunque 3 +
6 + 3 = 12:
Eser cizio 1.60 Sia B un’algebra finita e x 2 B : Esprimere x0 in funzione
degli atomi di B:
Soluzione. Vale at(x0 ) = (at(x))c : Infatti, per ogni atomo a, a 2 at(x0 ) sse
a · x0 sse a £ x (altrimenti, per Th.1.46.6,
avremmo a · 0) sse a 2
= at(x)
W
c
0
sse a 2 (at(x)) : Pertanto x =
a :
a2(at(x))c
Eser cizio 1.61 Sia B un’algebra finita di 2n elementi, con n > 1. Dimostrare
che un qualunque insieme di n ¡ 1 atomi genera B.
Soluzione. Sia At(B) = fa1; :::; an g e si consideri la sottalgebra di B generata
0
da a1; :::; an¡1. Essendo an = (a1 _ ::: _ an¡1) (cfr. il precedente Esercizio
1.60) tale sottalgebra contiene tutti gli atomi di B e quindi coincide con B:
Ricordiamo che un termine booleano ®(x1; :::; xn ) in n variabili è detto conn
V
giunzione elem entar e se ha la forma
x~i, dove, per ogni i · n, x~i = xi
i=1
oppure ~xi = x0i : Essendovi due possibilità per ciascun x~i ; le possibili congiunzioni elementari di x1; :::xn sono 2n :
Teor ema 1.62 Sia B l’algebra di Boole generata da Y = fg 1; :::gn g : Siano
® 1(x1; :::; xn); :::; ® m(x1; :::; xn), con m = 2n , le congiunzioni elementari in
n variabili e sia I = fi 2 N : 1 · i · mg :
(1) Ogni atomo di B ha la forma ® [g 1; :::gn ], dove ® è congiunzione elementare in n variabili.
(2) Data una congiunzione elementare ®; ® [g 1; :::gn ] è un atomo di B oppure
è 0.
(3) Date due congiunzioni elementari ® 1(x1;1; :::; x1;n) e ® 2 (x2;1; :::; x2;n ); se
® 1 6= ® 2 e ® 1 [g1 ; :::g n] e ® 2 [g1; :::g n] sono atomi, allora tali atomi sono diversi.
4) (Teorema di forma nor male ) Ogni elemento di B ha la forma
_
® j [g 1; :::gn ]
j2J
con J µ I, intendendo 0 =
5) C ard(At(B)) · 2n;
W
j2;
® j [g1; :::g n] :
36
n
6) C ard(B) · 22 :
I precedenti risultati ci forniscono il seguente
Algor itmo per deter m inar e l’algebr a gener ata da un insiem e finito Y =
fg 1; :::gn g di gener ator i:
1.
2.
trovare tutti gli elementi della forma ® [g 1; :::; g n], dove ®(x1; :::; xn ) è
una n-congiunzione elementare. Tali elementi, se non sono lo 0, sono
atomi (distinti per congiunzioni distinte) della generanda algebra. In
questo modo si identificano tutti gli m · 2n atomi di tale algebra;
W
effettuare i 2m possibili supremi di atomi (considerando
ai = 0); in tal
i2;
modo si ottengono i 2m elementi dell’algebra generata (Th.1.55).
O sser vazione 1.63 Il punto (4) è un rafforzamento del Teorema 1.40 per algebre finite. Rispetto al Teorema 1.40, il precedente algoritmo ha il vantaggio
di fare riferimento alle sole congiunzioni elementari in n variabilI, in cui inoltre
ciascuna variabile è interpretata su un diverso elemento di Y .
E sem pio 1.64 Si considerino gli insiemi X = f1; 2; 3g ; Y = f2; 3; 6g e
Z = f1; 6g ; sottinsiemi dell’universo U = f1; 2; 3; 4; 5; 6g : Per determinare la sottalgebra di P (U ) generata da fX; Y; Z g individuiamo dapprima gli
elementi della forma ® [X; Y; Z] ; dove ® è una congiunzione elementare in 3
variabili:
X \ Y \ Z = ;;
X c \ Y \ Z = f6g
X \ Y \ Z c = f2; 3g ;
X c \ Y \ Zc = ;
X \ Y c \ Z = f1g ;
X c \ Y c \ Z = ;;
X \ Y c \ Z c = ;;
X c \ Y c \ Z c = f4; 5g :
Gli elementi diversi da ; sono solo 4, in quanto 4 delle 8 congiunzioni elementari ®(x1; x2; x3), interpretate su X; Y; Z , sono risultate uguali al vuoto.
Facendo tutte le possibili unioni di f1g ; f6g ; f2; 3g e f4; 5g otteniamo, essendo tali elementi a due a due disgiunti, 24 = 16 elementi (si ricordi che si
considera anche l’unione vuota).
E ser cizio 1.65
in figura.
Sia U un insieme e X; Y due sottinsiemi di U disposti come
X
Y
Esprimere gli elementi della sottalgebra di P (U ) generata da fX; Y g in termini di X e Y .
37
Soluzione. Gli elementi di P (U ) della forma ® [X; Y ] ; dove ® è una congiunzione elementare in 2 variabili, sono:
A1 = X \ Y c ; A2 = X \ Y ; A3 = X c \ Y ; A 4 = X c \ Y c :
Nessuno di tali elementi è uguale al ;: Essendo tali elementi a due a due disgiunti, otteniamo, considerando i sottinsiemi di fA1; A 2; A3 ; A4g ; 24 = 16
elementi. Nella seguente tabella scriviamo, quando esiste, una espressione
semplificata dell’unione ottenuta:
;
fA1g
fA2g
fA3g
fA4g
fA 1; A 2g
fA 1; A 3g
fA 1; A 4g
fA 2; A 3g
fA2 [ A4g
fA3 [ A4g
fA1 [ A2 [ A3g
fA1 [ A2 [ A4g
fA1 [ A3 [ A4g
fA2 [ A3 [ A4g
fA1 [ A2 [ A3 [ A4g
$
$
$
$
$
$
$
$
$
$
$
$
$
$
$
$
;
A1
A2
A3
A4
X
A1 [ A3
A1 [ A4
Y
A2 [ A4
Xc
X [Y
X[Yc
(X \ Y )c
Xc [ Y
U
Eser cizio 1.66 Sia U un qualunque insieme non vuoto e siano X e Y due
insiemi tali che ; ½ X ½ Y ½ U: Dire da quanti elementi è composta la sottalgebra di P (U ) generata da fX; Y g :
Soluzione 1 (In modo meccanico, tramite congiunzioni elementari). Consideriamo gli elementi della forma ® [X; Y ] ; dove ® è una congiunzione elementare in 2 variabili:
X \ Y ; X \ Y c; X c \ Y ; X c \ Y c
Essendo X µ Y; abbiamo X \ Y c = ;: Gli altri tre elementi sono A 1 =
X \ Y = X; A 2 = X c \ Y e A 3 = X c \ Y c = Y c. Le 23 possibili unioni di
tali elementi ci danno gli otto elementi dell’algebra.
Soluzione 2 (Senza passare per il concetto di congiunzione elementare). Aiutandoci con i diagrammi vediamo che l’algebra generata dai due insiemi è composta dai seguenti 8 elementi:
38
A0 =
A1 =
A2 =
A3 =
A4 =
A5 =
A6 =
A7 =
; (= X \ X c)
X
Xc \ Y
Yc
Y
X[Yc
Xc
U (= X [ X c)
X
1
2
Y
4
3
X
X
XX
X
Y
YY
Y
0
XX
X
X
Y
XX
Y
Y
Y
5
6
7
Tali elementi corrispondono ai modi con cui è possibile colorare il diagramma
comprendente i due insiemi impiegando un solo colore (oltre al bianco) e senza
uscire dai confini che delimitano i due insiemi.
O sser vazione 1.67 Se C è un algebra di insiemi generata da X 1; :::; Xn e se
tali insiemi sono rappresentati mediante diagrammi di Venn, allora
ciascun atomo corrisponde ad una ‘parte indivisa’
cioè una parte di diagramma non tagliata da alcun insieme, purché però gli insiemi siano disegnati in modo che ognuna di tali parti sia caratter izzabile in
ter mini di X1; :::; X n. Facciamo un esempio. Nel diagramma di sinistra ogni
parte indivisa è caratterizzabile in termini di X e Y : 1 = X c \Y c , 2 = X \Y c,
3 = X \ Y , 4 = X c \ Y . Anche nel diagramma al centro ciò accade: 1 = X c,
2 = X \ Y c , 3 = Y .In quello di destra, invece, le due parti contrassegnate con
2 costituiscono, insieme, X \ Y c , e non è possibile distinguerle riferendosi X
e Y . Lo stesso accade per le due parti segnate con 4, che costituiscono X c \ Y:
L’impiego dei diagrammi di Venn richiede quindi un po’di cautela (cfr. anche
Esercizio ??).
1
4
1
2
3
X
4
2
2
3
X
Y
4
Y
Gener ator i liber i
Definizione 1.68 Sia B un’algebra di Boole generata da g 1; :::gn : Definiamo tali generatori liber i se, per ogni congiunzione elementare ®(x1; :::; xn ),
abbiamo
® [g 1; :::gn ] 6= 0:
39
Un’algebra generata da un insieme di n generatori liberi prende il nome di
algebr a liber a su n gener ator i.
Ad esempio, gli insiemi X; Y dell’Es.?? non sono liberi, mentre lo sono quelli
dell’Es.1.65.
Teor ema 1.69 Se i generatori g 1; :::gn di un’algebra B sono liberi allora C ard(B) =
n
22 :
Dimostrazione. Dal Teorema 1.62 segue che, per ogni congiunzione elementare ®(x1; :::; xn); l’elemento ® [g1 ; :::g n], essendo diverso da 0, è un atomo. Inoltre, date due congiunzioni elementari ® 1(x1; :::; xn ) e ® 2(x1; :::; x;
se ® 1 6= ® 2 allora ® 1 [g 1; :::g n] 6= ® 2 [g 1; :::gn ]. Pertanto B ha 2n atomi, tanti
n
quanti le congiunzioni elementari di n variabili e quindi C ard(B) = 22 :
¹ ; _;
¹ :
Esempio 1.70 nSi consideri l’algebra
F n = (F n ; ^
¹ ; ?; >) dell’Esempio
o
n : i · n
1.27. L’insieme [pi ]´
è un insieme di generatori liberi. Che si tratti
di un insieme di generatori è ovvio: ogni formula in n variabili è scritta a
partire da tali variabili. Che i generatori siano liberi risulta invece dal fatto che
nessuna congiunzione elementare p~1 ^ ::: ^ p~n è una contraddizione (esistendo
una valutazione che la soddisfa). Quindi, per ogni n, F n è un’algebra libera su
n generatori.
Il seguente Esempio dà un esempio esplicito di n insiemi liberi.
Esempio 1.71 Per ogni n 2 N, esiste U ed esistono n insiemi X 1; :::; Xn µ
U che sono un insieme di generatori liberi per P (U ): Infatti, dato n, considen
riamo l’insieme U = f0; 1g costituito dalle 2n n-ple ordinate di 0 e di 1. Per
ogni i · n poniamo
Xi = fv 2 U : v(i) = 1g
dove con v(i) intendiamo l’i-esima componente della n-pla v. Tali insiemi
~1 \ X
~2 \
X 1; :::; Xn sono liberi. Infatti, data una qualunque intersezione X
~ n; dove X
~i è Xi o X c ; si consideri l’elemento v 2 U così definito:
::: \ X
i
¿
~i = X c;
0 se X
i
per ogni i · n, v (i) =
~i = X i:
1 se X
~1 \ X
~ 2 \ :::\ X
~ n e quindi X
~1 \X
~ 2 \ :::\ X
~ n 6= ;: In tal modo,
Abbiamo v 2 X
per ogni congiunzione elementare ®(x1; :::; xn ), abbiamo ® [X1 ; :::; X n] 6= 0:
Ad esempio, per n = 3 abbiamo X 1 = f(1; 0; 0); (1; 0; 1); (1; 1; 0); (1; 1; 1); g,
X 2 = f(0; 1; 0); (0; 1; 1); (1; 1; 0); (1; 1; 1)g e X3 = f(0; 0; 1); (0; 1; 1); (1; 0; 1); (1; 1; 1)g :
Per n =
½ 4 abbiamo:
¾
(1; 0; 0; 0); (1; 0; 0; 1); (1; 0; 1; 0); (1; 0; 1; 1);
X1 =
(1; 1; 0; 0); (1; 1; 0; 1); (1; 1; 1; 0); (1; 1; 1; 1)
40
X2 =
X3 =
½
(0; 1; 0; 0); (0; 1; 0; 1); (0; 1; 1; 0); (0; 1; 1; 1);
(1; 1; 0; 0); (1; 1; 0; 1); (1; 1; 1; 0); (1; 1; 1; 1)
½
(0; 0; 1; 0); (0; 0; 1; 1); (0; 1; 1; 0); (0; 1; 1; 1);
(1; 0; 1; 0); (1; 0; 1; 1); (1; 1; 1; 0); (1; 1; 1; 1)
¾
¾
(0; 0; 0; 1); (0; 0; 1; 1); (0; 1; 0; 1); (0; 1; 1; 1);
:
(1; 0; 0; 1); (1; 0; 1; 1); (1; 1; 0; 1); (1; 1; 1; 1)
Si pone questo problema: come rappresentare n insiemi liberi mediante un
diagramma di Venn?
Qui di seguito presentiamo il caso per n = 2 e n = 3; per i quali esiste una
rappresentazione visivamente molto chiara.
X4 =
½
¾
Z
X
Y
X
Y
Per una fallace generalizzazione dei casi n = 2 e n = 3 , potremmo pensare
che i quattro insiemi del successivo diagramma a sinistra siano liberi. Così
non è. Quel diagramma contiene infatti 14 parti indivise mentre, se gli insiemi
fossero liberi, nessuna congiunzione elementare in 4 variabili individuerebbe il
; e quindi le parti indivise dovrebbero essere 24 = 16: Nel nostro caso, invece,
X 1 \ X2c \ X3 \ X 4c = ; e X 1c \ X 2 \ X3c \ X4 = ;: L’algebra generata ha
dunque ’’soltanto’’214 = 16384 elementi. I quattro insiemi del diagramma di
destra sono invece liberi. Come si vede, questa volta abbiamo 16 parti indivise,
corrispondente ciascuna ad una congiunzione elementare. L’algebra generata
ha quindi 216 = 65536 elementi.
X
t
Y
z
Z
T
x
y
X; Y; Z; T non liberi
X; Y; Z; T liberi
E ser cizio 1.72 Si considerino gli insiemi X = f1; 2; 3g ; Y = f2; 3; 6g e
Z = f1; 6g ; sottinsiemi dell’universo U = f1; 2; 3; 4; 5; 6g : (a) Individuare
la sottalgebra C di P (U ) generata da X; Y; Z . (b) Dire se X; Y; Z sono liberi. In caso negativo trovare, se esiste, un insieme di generatori liberi per C. (c)
Dire X; Y; Z costituiscono un insieme di generatori irriducibile e, in caso negativo, trovarne un sottinsieme irriducibile.
41
Soluzione. Il primo punto della procedura per determinare C consiste nell’individuare i suoi atomi:
X \ Y \ Z = ;, X \ Y \ Z c = f2; 3g = b1, X \ Y c \ Z = f1g = b2,
X \Y c \Z c = ;, X c \Y \Z = f6g = b3, X c \Y \Z c = ;, X c \Y c \Z = ;,
X c \ Y c \ Z c = f4; 5g = b4.
Gli atomi sono solo 4, in quanto 4 delle 8 congiunzioni elementari in tre variabili individuano il vuoto (X; Y; Z non sono quindi generatori liberi). Il secondo
punto della procedura consiste nel fare tutte le possibili unioni di atomi. La
sottalgebra ha pertanto i seguenti 24 = 16 elementi: ;; b1; b2; b3; b4; b1 [ b2 ;
b1 [ b3; b1 [ b4; b2 [ b3; b2 [ b4 ; b3 [ b4; b1 [ b2 [ b3; b1 [ b2 [ b4; b1 [ b3 [ b3 ;
b2 [ b3 [ b4; b1 [ b2 [ b3 [ b4(= U ):
Poiché X \ Y c = f1g e Y \X c = f6g, abbiamo Z = (X \ Y c ) [ (Y \ X c ) :
Pertanto fX; Y g è un insieme di generatori per C e dunque fX; Y; Zg non è
2
un insieme irriducibile. Essendo 16 = 22 , fX; Y g è un insieme di generatori liberi per C: Ciò si verifica anche in modo diretto, osservando che le
quattro congiunzioni elementari in due variabili individuano i quattro atomi:
X \ Y; X \ Y c ; X c \ Y; X c \ Y c:
Eser cizio 1.73 Trovare il numero degli elementi delle sottalgebre di P (U )
generate dalle terne di insiemi X; Y; Z rappresentati nei 4 diagrammi seguenti.
X
X
Z
Y
Z
2
Y
1
Z
1
2
5 8 6
2
4
7
X
1
Z
3
Y X
3
4
3
Y
4
Soluzione. I diagrammi contengono nell’ordine 5, 6, 5 e 8 parti indivise (cioè
atomi), e quindi le rispettive algebre generate hanno 25 = 32, 26 = 64; 25 =
32 e 28 = 256 elementi. Solo nel quarto diagramma, essendo 8 = 23 ; nessuna
congiunzione elementare corrisponde al vuoto e X; Y; Z sono liberi.
X
5
4
Z
2
Z
Y
2
3
X
4
3
5 6
5
Z
Y
2
3
1
1
1
2
4
1
X
1
3
Z
4
X
Y
5
2
8
6
4
7
3
Y
42
1.8
Isomor fism i
Definizione 1.74 Siano B 1 = (B1; _ 1; ^1;0 1 ; 01; 11) e B2 = (B2; _2; ^2 ;0 2 ; 02; 12 )
due algebre di Boole. Una funzione © da B1 a B 2 si dice un isomor fism o tra
tali algebre se soddisfa le seguenti condizioni:
1) © è biettiva;
2) per ogni x; y 2 X1; ©(x ^1 y) = ©(x) ^ 2 ©(y );
3) per ogni x; y 2 X1; ©(x _1 y) = ©(x) _ 2 ©(y );
4) per ogni x 2 X 1; ©(x01 ) = ©(x)0 2 :
A parole, le condizioni (2) e (3) asseriscono che, per ogni coppia di elementi x; y della prima algebra, l’immagine mediante la © dell’infimo (supremo)
tra x e y coincide con l’infimo (supremo) delle le loro immagini.1 E’ immediato osservare come la relazione di isomorfismo tra algebre di Boole sia una
relazione di equivalenza. Due algebre di Boole B 1e B2 tra le quali esiste un
isomorfismo si dicono isom or fe. In simboli,B1 »
= B2:
Le condizioni (2)-(4) possono essere espresse in modo equivalente come segue:
per ogni x; y 2 X1; x ^1 y = z se e solo se ©(x) ^2 ©(y) = ©(z);
per ogni x; y 2 X1; x _1 y = z se e solo se ©(x) _2 ©(y) = ©(z);
0
per ogni x 2 X 1; x01 = y se e solo se (©(x)) 2 = ©(y):
In tal modo, se due algebre sono isomorfe allora qualunque proprietà (purché
espressa con riferminento alle operazioni coinvolte dall’isomorfismo) vale nell’una se e solo se vale nell’altra. Da questo punto di vista, due strutture isomorfe sono strutturalmente identiche. Ad esempio:
1) ©(01) = 02;
2) ©(11) = 12;
3) per ogni x; y 2 B1; x ·1 y se e solo se ©(x) ·2 ©(y);
4) a è un atomo di B1 se e solo se ©(a) è un atomo di B2;
5) X è una sottalgebra di B1 se e solo se f©(x) : x 2 Xg è una sottalgebra di
B2 ;
6) Y è un insieme di generatori di B1 se e solo se f©(g) : g 2 Y g è un insieme
di generatori di B2 :
Uno dei risultati caratterizzanti la teoria delle algebre di Boole è il
Teor ema di r appr esentazione di Stone. Ogni algebra di Boole è isomorfa ad
un’algebra di insiemi.
Di conseguenza, le algebre di insiemi sono in grado di rappresentare l’intera classe delle algebre di Boole: se qualche proprietà (che sia esprimibile in
termini di operazioni booleane) vale in ogni algebra di insiemi, allora vale in
1
Dalle identità x ^ y = (x 0 _ y 0 ) 0 e x _ y = (x 0 ^ y 0 ) 0 segue che, nella definizione di
isomorfismo, una tra le condizioni (2) e (3) è superf lua.
43
ogni algebra di Boole. La forza di questo risultato è notevole. Un esempio:
nel Teorema 1.46 abbiamo elencato un certo numero di proprietà della relazione · nelle algebre di Boole. Salvo che per la prima, non abbiamo svolto la
dimostrazione, che sarebbe risultata laboriosa in quanto, in assenza di una interpretazione privilegiata per le operazioni, avremmo potuto ricorrere solo agli
assiomi della teoria. Ora, in virtù del Teorema di Stone, sappiamo che se una
proprietà è valida interpretando · come la relazione µ di inclusione tra insiemi
allora è valida per ogni algebra di Boole, e la dimostrazione di quelle proprietà,
riferendosi alla relazione µ; è immediata.
Omettiamo la dimostrazionedel teorema di Stone. Nel caso delle algebre finite,
possiamo tuttavia descrivere la forma assunta dall’isomorfismo.
Teor ema 1.75 (Teorema di Stone per algebre di Boole finite ) Sia B = (B; _; ^;0 ; 0; 1)
un’algebra di Boole finita. Allora B è isomorfa all’algebra di insiemi (P (At(B)); \; [;c ; ;; At(B)),
e la funzione di isomorfismo è la seguente:
©(b) = at(b):
Cor ollar io 1.76 Due algebre finite B e C aventi la stessa cardinalità sono
isomorfe.
Dimostrazione. Per il Teorema di Stone, B »
= P (At(B)) e C »
= P (At(C)), da
cui segue che C ard(At(B))
=
C
ard(At(C)):
Esiste
allora
una
biezione f da
W
At(B) ad At(C): Sia x =
a, con X µ At(B): La funzione
a2X
©(x) =
_
f (a)
a2X
è un isomorfismo tra B e C.
Come osservato, due algebre isomorfe sono indistinguibili se ci si riferisce a
proprietà esprimibili nei termini delle operazioni coinvolte dall’isomorfismo
stesso; sono cioè strutturalmente uguali. Per tale motivo dal teorema precedente, e dal Corollario 1.56, deriva che, fissato un cardinale m, se m non è una
potenza di 2 allora non vi sono algebre di Boole di m elementi, mentre se è una
potenza di 2 allora ve ne è una e, a meno di isomorfismo, una sola. Questa proprietà segnala che gli assiomi della teoria delle algebre di Boole sono ‘‘forti’’,
in grado cioè di limitare la varietà tra le strutture che li soddisfano.
» F n:
Teor ema 1.77 Se B è un’algebra libera su n generatori allora B =
Dimostrazione. F n è libera su n generatori (cfr. Esempio 1.70), e dal Teoren
ma 1.76 segue che due algebre libere su n generatori, avendo entrambe 22
elementi, sono isomorfe tra loro.
44
E ser cizio 1.78 Siano B1 e B2 due algebre di Boole finite aventi lo stesso
numero m di elementi. Dire quanti sono i possibili isomorfismi tra B 1 e B2.
Soluzione. Gli isomorfismi sono tanti quanti le possibili biezioni tra gli atomi.
Essendo C ard(At(B1 )) = C ard(At(B2)) = n, con n = log2 m; le possibili
biezioni da At(B1) ad At(B2) sono n!.
(Osservazione: Ponendo B1 = B2 = B otteniamo che gli automorfismi di B
sono n!:)
E ser cizio 1.79 Sia B = (B; _; ^ 0 ) un’algebra di Boole. Dimostrare che la
funzione, da B a B , così definita:
©(x) = x0
è un isomorfismo tra B = (B ; _; ^;0 ) e B2 = (B; _ 2; ^2;02 ) dove _2 =
^; ^ 2 = _ e 02 = 0 :
Dimostr azione. (Attenzione: non si tratta di automorfismo, in quanto abbiamo
due algebre diverse, pur se sullo stesso dominio).
©(x ^ y) = (x ^ y) 0 = x0 _ y 0 = x0 ^2 y 0 = ©(x) ^ 2 ©(y): Analogamente
per _: Infine ©(x0 ) = x00 = (©(x)) 0 : Tale isomorfismo scambio 0 con 1 e ·
con > :
E ser cizio 1.80 Si considerino l ’algebra P (fa; b; cg) e l’algebra C generata
da due insiemi disgiunti e non vuoti X; Y µ U: Dire se sono isomorfe.
Soluzione. Si. Entrambe sono atomiche (in quanto finite) e hanno 3 atomi e
8 elementi. Per definire un isomorfismo è sufficiente indicare una corrispondenza tra gli atomi. Ad esempio:
©(a) = X
a
©(b) = Y
b
c
©(c) = U ¡ (X [ Y )
X
Y
U
La figura può indurre a pensare che la funzione © inserisca una difformità nel
trattamento di c rispetto ad a e b, difformità assente in P (fa; b; cg : Ma non
bisogna farsi ingannare: la forma che nel diagramma assumono gli atomi (e
quindi la diversità di U ¡ (X [ Y ) rispetto a X e Y ) è inessenziale. Come mostra la figura successiva, è possibile disegnare gli insiemi in modo da far sparire
ogni asimmetria; le diversità tra i diagrammi della linea superiore e quelli della
linea inferiore, pur essendo rilevante sotto molti aspetti, ad esempio topologici, non lo è da un punto di vista algebrico
45
a
b
c
a
b
a
b
c
a
b
c
X
Y
X
Y
c
Eser cizio 1.81 Trovare, se esiste, un insieme di generatori liberi per l’algebra
P (U ); con U = fa; b; c; dg :
2
Soluzione. C ard(P (U )) = 24 = 22 : Pertanto P (U ) »
= F 2 e quindi P (U ) ha
un insieme di due generatori liberi. Per determinarli, impieghiamo il Teorema
??.7. Troviamo una biezione ª tra
At(F2 ) = f[:p ^ :q]´ ; [:p ^ q]´ ; [p ^ :q]´ ; [p ^ q]´g
e
At(P (U )) = ffag ; fbg ; fcg ; fdgg ;
ad esempio ª([:p ^ :q]´ ) = fag ; ª([:p ^ q]´) = fbg ; ª([p ^ :q]´ ) =
fcg ; ª([p ^ q]´) = fdg : ª è estendibile ad un isomorfismo ©, e in un isomorfismo i generatori liberi si corrispondono. Essendo [p]´ e [q]´ generatori
liberi di F 2; ed essendo p ´ (p ^ q) _ (p ^ :q) e q ´ (:p ^ q) _ (:p ^ q)
otteniamo:
©([p]´ )
©([q]´ )
=
=
¹
©([p ^ q]´)_©([p
^ :q]´) = fdg [ fcg = fc; dg
¹
©([p ^ q]´)_©([:p
^ q]´) = fdg [ fbg = fb; dg
L’insieme ffb; dg ; fc; dgg è un insieme di generatori liberi per P (U ).
Eser cizio 1.82 Sia C l’algebra di insiemi generata da tre sottinsiemi liberi
X; Y; Z di U . Dire se C è isomorfa a F3 :
Soluzione. Si. F 3 è generata da [p]´ ; [q]´ ; [r]´, che sono liberi (cfr Esempio
3
1.52). Entrambe le algebra hanno quindi 22 = 256 elementi e sono isomorfe.
1.9
Rappresentazione di algebre di Boole con diagr ammi
Nella Figura sono rappresentate le algebre di 2, 4, 8 e 16 elementi (si ricordi
che le algebre finite hanno come cardinalità una potenza di 2 e che, a meno di
isomor fismo, vi è un’unica algebra per ciascuna di tali cardinalità).
46
sup. di 4 atomi
sup. di 3 atomi
sup. di 2 atomi
atomi
sup. di 0 atomi
Poiché in un’algebra di Boole finita ogni elemento è supremo di atomi, nel
diagramma di Hasse di un’algebra di 2n elementi è possibile disporre gli elementi
¡ n¢ su n + 1 livelli, da 0 ad n. Al livello k, per 0 · k · n; si trovano gli
k elementi che sono supremo di un sottinsieme di k degli n atomi (ponendo
sup ; = 0). In ciascuna algebra troviamo quindi, livello per livello, i numeri
di una riga del triangolo di Tartaglia (v. figura successiva). Inoltre, a ciascun
punto x di livello k arrivano (dal livello inferiore) k segmenti,
¡ k ¢ precisamente
dai k elementi di livello k ¡ 1 che sono supremo dei k = k¡1
sottinsiemi di
k ¡ 1 dei k atomi di cui x è supremo.
1
1
1
1
1
1
2
3
4
5
1
1
3
6
10
1
4
10
1
1
1
Mentre le operazioni reticolari ^ e _ sono chiaramente visualizzate nei diagrammi di Hasse, non altrettanto avviene, nel caso delle algebre di Boole, per
l’operazione di complemento. Possiamo tuttavia osservare questo fatto. Sia
At(B) l’insieme degli
Watomi di0un’algebra
W B finita: Dato un qualunque elemento x, abbiamo x =
a ex =
a: Supponiamo C ard(At(B)) =
a2at(x)
a2At(B)¡at(x)
n e C ard(at(x)) = k: Allora x si trova al livello k e¡il¢suo ¡complementare
x0
n
n ¢
si trova al livello n ¡ k (in questo contesto, l’identità k = n¡k corrisponde
all’iniettività della funzione 0 : tanti elementi, altrettanti complementari). Nella
figura successiva abbiamo nominato con lettere la prima metà degli elementi (partendo dal basso e, all’interno di ciascun livello, da sinistra); la seconda
metà è costituita dai loro complementari. In tal modo otteniamo la seguente visualizzazione: il complementare di un elemento si trova nel punto simmetrico
rispetto al centro di simmetria segnato con un asterisco.
47
0'
0'
0'
c'
b'
a'
b
c
e
d'
c'
f
g
a
b
*
0'
*
0
a
*
a'
0
a
0
*
b'
a'
g'
f'
c
d
e'
0
Centro di simmetria per il complementare
1.10 Identità valide
Per definizione, una identità ® = ¯ tra termini booleani è valida se è soddisfatta per ogni interpretazione in qualunque algebra di Boole. Naturalmente,
a causa del riferimento alla totalità degli elementi della totalità delle algebre,
da tale definizione non deriva un metodo per determinare in modo effettivo la
validità di una identità. In virtù del Teorema di Stone, invece di considerare
la classe di tutte le algebre di Boole possiamo limitarci alle algebre di insiemi.
In tal modo possiamo costantemente interpretare le operazioni booleane con le
operazioni insiemistiche \; [;c e le variabili che compaiono nei termini booleani come sottinsiemi X 1; :::; Xn di qualche universo U . (Per una maggiore
intuitività, scriveremo quindi i termini booleani (v. Definizione 1.34) impiegando i simboli \; [;c al posto di ^; _;0 .). Il riferimento a tutte le algebre di
insiemi è comunque sempre tale da inibire un metodo effettivo.
Una drastica semplificazione è offerta dal metodo delle Tavole di appartenenza
(che abbiamo incontrato a Fondamenti di algebra), che costituisce un metodo
effettivo. Lo riassumiamo brevemente:
Siano X1; :::; X n sottinsiemi di un insieme U e sia a un qualunque elemento di
U: Tale elemento può appartenere o non appartenere ad X 1, appartenere o non
appartenere ad X 2, e così via fino a n: Esistono pertanto 2n diverse situazioni
di appar tenenza di a rispetto a X 1; :::; Xn ; ciascuna delle quali può essere
rappresentata da una sequenza
~ 1; :::; 2
~ n)
s = (2
~ i è 2 oppure 2
dove, per ogni i · n, 2
= : Si consideri ora un termine ® in
x1; :::xn; Per costruire la tavola di appar tenenza per ® bisogna elencare tutte le 2n possibili situazioni di appartenenza e, per ognuna, determinare l’appartenenza di un generico a ai vari insiemi individuati dalle sottotermini che
48
compongono ®. Il comportamento delle varie operazioni insiemistiche rispetto all’appartenenza si desume dalla loro definizione, ed è rappresentato dai
seguenti schemi:
®
2
=
2
=
2
2
¯
®\ ¯
2
=
2
=
2
2
=
2
=
2
=
2
2
intersezione
®
2
=
2
=
2
2
¯
®[¯
2
=
2
=
2
2
2
=
2
2
2
unione
®
2
=
2
®c
2
2
=
complemento
Ad esempio, la tavola di appartenenza del termine ® : (x [ y) \ (y c [ x) è
x
y
yc
x[y
yc [ x
(x [ y ) \ (y c [ x)
2
=
2
=
2
2
2
=
2
2
=
2
2
2
=
2
2
=
2
=
2
2
2
2
2
=
2
2
2
=
2
=
2
2
Data una situazione di appartenenza s relativa ad n insiemi e dato un termine
® in n variabili, scriviamo
s(®)
per indicare il valore che compare nella colonna finale della tavola di appartenenza di ® in corrispondenza della situazione s: Ad esempio se s = (2; 2
=) e
® è il termine (x [ y) \ (y c [ x) dell’esempio precedente, allora s(®) =2; essendo questo il valore della colonna finale della tavola di ® in corrispondenza
dell’assegnazione (2; 2
= ); cioè nella terza riga.
Teor ema 1.83 Dato un insieme U , dato a 2 U , dati X 1; :::; Xn µ U e data
~ 1 ; :::; 2
~ n) di a rispetto a X1 ; :::; Xn , vale
la situazione di appartenenza s = (2
che:
a 2 ® [X 1; :::; Xn ] se e solo se s(®) =2 :
Dimostr azione. Per induzione sulla costruzione del termine ®: (Attenzione: alcuni passaggi sono fin troppo ovvi).
Se ® è una variabile (base di induzione), cioè ® = x, allora la tavola di appartenenza di ® coincide con la colonna della variabile x. Ma anche ® [X] = X
e quindi l’asserto dice che a 2 X sse s(®) =2, i.e. sse a 2 X:
Affrontiamo i tre passi induttivi, uno per ciascun passo nella costruzione dell’insieme dei termini.
Supponiamo ® = ¯ c: Allora a 2 ® [X1; :::; X n] sse a 2
= ¯ [X1; :::; X n] sse,
per ipotesi induttiva, s(®) = 2
= ; sse s(¯ ) =2 :
49
Supponiamo ® = ¯ \ °: Allora a 2 ® [X 1; :::; Xn ] sse a 2
e a 2 ° [X 1; :::; Xn ] sse, per ipotesi induttiva, s(¯ ) =2 e
s(®) =2 :
Supponiamo ® = ¯ [ °: Allora a 2 ® [X 1; :::; Xn ] sse a 2
o a 2 ° [X 1; :::; Xn ] sse, per ipotesi induttiva, s(¯ ) =2 o
s(®) =2 :
¯ [X 1; :::; Xn ]
°(s) =2; sse
¯ [X 1; :::; Xn ]
°(s) =2; sse
Diciamo che due termini booleani ® e ¯ in n variabili hanno la stessa tavola di
appar tenenza se hanno uguale la colonna finale delle rispettive t.d.a. (Nel caso siano in un numero diverso di variabili, si parifica fittiziamente tale numero
congiungendo termini della forma ::: \ (xi _ xci ). Vale il seguente risultato.
Teor ema 1.84 L’identità ® = ¯ è valida se e solo se ® e ¯ hanno la stessa
tavola di appartenenza.
Dimostrazione. Supponiamo dapprima che ® e ¯ abbiano la stessa tavola di
appartenenza. Siano X1 ; :::; X n sottinsiemi di un qualunque universo U; sia
~ 1; :::; 2
~ n ) la situazione di appartenenza di a rispetto a
a 2 U e sia s = ( 2
X 1; :::; Xn . Per l’uguaglianza delle tavole di ® e ¯ , s(®) = s(¯) e quindi, per
il Teorema 1.83, a 2 ® [X 1; :::; Xn ] se e solo se a 2 ¯ [X1 ; :::; X n] : Poiché ciò
vale per ogni a 2 U; abbiamo ® [X 1; :::; Xn ] = ¯ [X 1; :::; Xn ], e poiché ciò
accade per ogni n-pla di insiemi X1 ; :::; X n di qualunque universo U , abbiamo
che ® = ¯ vale in ogni algebra di insiemi. Pertanto, per il Torema di Stone,
l’identità ® = ¯ è valida. Viceversa, supponiamo che ® = ¯ sia valida e
~ 1; :::; 2
~ n ) una qualunque situazione d’appartenenza. E’immediato
sia s = (2
trovare n insiemi X 1; :::; Xn (non necessariamente distinti) di un universo U
e un elemento a 2 U tale che la situazione di appartenenza di a rispetto ad
X 1; :::; Xn sia s: (Il modo più semplice è il seguente: scelto un qualunque U ,
si pone
¿
~ i =2;
U se 2
Xi =
)
~ i =2
; se 2
= :
Dalla validità di ® = ¯ segue ® [X1; :::; Xn ] = ¯ [X1 ; :::; X n] e quindi, per
il Teorema 1.83, s(®) = s(¯ ). Poiché ciò accade per ogni s, ® e ¯ hanno la
stessa tavola di appartenenza.
La prima conseguenza, largamente prevedibile, del Teorema 1.84 è questa:
Cor ollar io 1.85 L’identità ® = ¯ è valida se e solo se, dopo la trasformazione dei termini ® e ¯ nelle formule proposizionali ® f e ¯ f ; ottenuta sostituendo
ordinatamente le variabili booleane con lettere proposizionali e le generiche
operazioni booleane (che in questa sezione indichiamo con \; [;c ) con i connettivi logici ^; _; :; la formula ® f $ ¯ f è una tautologia.
Altre conseguenze altrettanto immediate del Teorema 1.84, ma non altrettanto
prevedibili, sono le seguenti:
50
Cor ollar io 1.86 ® = ¯ è valida se e solo se è vera in una singola generica
algebra B.
Dimostr azione. L’implicazione ()) è ovvia. Viceversa, supponiamo che ® =
¯ non sia valida. Allora, per il Teorema 1.84, ® e ¯ hanno tavole di apparte~ 1; :::; 2
~ n ) una situazione rispetto alla quale ® e ¯ si
nenza diverse. Sia s = ( 2
comportano in modo diverso: ad esempio, supponiamo s(®) =2 e s(¯) = 2
=.
Sia C un’algebra di insiemi su un universo U tale che C »
= B: Per ogni i · n
poniamo
¿
~ i =2;
U se 2
Xi =
~
; se 2i = 2
= :
In tal modo, preso un qualunque a 2 U , s è la situazione di appartenenza di a
rispetto a X1 ; :::; X n, per cui da s(®) =2 e s(¯ ) = 2
= segue, per il Th.1.83,
a 2 ® [X1; :::; X n] e a 2
= ¯ [X1 ; :::; X n]. Pertanto ® = ¯ è falsa in C; e quindi
in B:
Cor ollar io 1.87 Siano B1 e B2 due algebre di Boole. L’identità ® = ¯ è vera
in B1 se e solo se è vera in B 2:
Dimostr azione. Immediata dal corollario precedente.
Dal momento che la validità di una identità può essere verificata riferendosi ad
una singola algebra qualunque, è conveniente scegliere la più piccola algebra
possibile, cioè, riferendosi alle algebre di insiemi, f;; U g : Tale algebra viene
spesso indicata con 2. Bisogna però rimarcare che sull’algebra prescelta le
variabili devono essere interpretate in tutti i modi possibili. Quindi, se ® e ¯
sono termini in n variabili, pur riferendoci all’algebra 2 dovremo effettuare
2n verifiche, corrispondenti al numero dei modi di interpretare x1; :::; xn in
f;; U g.
E’possibile ridurre ulteriormente le operazioni da compiere per verificare la
validità di una identità, interpretando le variabili non più in tutti i modi possibili
sugli insiemi di una singola algebra, bensì su singoli fissati elementi di una
singola fissata algebra.
Teor ema 1.88 Siano ® e ¯ due termini in n variabili e B un’algebra libera su
n generatori g1 ; ::; gn . L’identità ® = ¯ è valida se e solo se ® [g 1; :::; gn ] =
¯ [g 1; :::; gn ].
Dimostr azione. Innanzitutto, per il Teorema di Stone possiamo supporre che
questa algebra libera sia un’algebra di insiemi, e continuare quindi ad usare il simbolismo insiemistico. Il verso ()) è conseguenza immediata delle
definizioni. Viceversa, supponiamo che ® = ¯ non sia valida. Allora, per
il Teorema 1.84, ® e ¯ non hanno la stessa tavola di appartenenza ed esi~ 1 ; :::; 2
~ n) tale che s(®) 6= s(¯ ); cioè s(®) =2 e
ste una situazione s = (2
s(¯ ) = 2;
= o viceversa. Consideriamo
l’intersezione ~g1 \ ~g2 \ ::: \ g~n do¿
~ i =2;
gi se 2
ve, per ogni i · n, g~i =
. Poiché g 1; :::; gn sono libe~ i =2
g ci se 2
=:
51
ri, ~g1 \ ~g2 \ ::: \ g~n 6= ; e quindi esiste un elemento a appartenente a tale
intersezione. Poiché la situazione di appartenenza di a rispetto a g1; :::; g n
è s; da s(®) =2 e s(¯) = 2
= segue, per la (1.83), che a 2 ® [g1; :::; g n] e
a2
= ¯ [g 1; :::; gn ] : Pertanto ® [g 1; :::; gn ] 6= ¯ [g1; :::; g n] :
La seguente tabella riassume l’evoluzione subita dai criteri per determinare
quando una identità è valida.
® = ¯ è valida se è soddisfatta da:
(Definizione)
tutte le interpretazioni in tutte le
algebre di Boole.
(Teorema di Stone)
tutte le interpretazioni in tutti le
algebre di insiemi
(Corollario 1.86)
tutte le interpretazioni in una sola
algebra (qualunque)
(Teorema 1.88)
una singola interpretazione su
generatori liberi.
Dunque, per il Teorema 1.88, se l’uguaglianza di termini booleani in n variabili è soddisfatta interpretando tali variabili su n insiemi liberi, allora vale in
qualunque algebra di Boole. Tuttavia, affinchè questo risultato possa costituire un test efficace, da contrapporre a quello delle tavole di appartenenza, è
necessario poter disporre di una buona rappresentazione ‘visiva’di tali insiemi, ottenuta ad esempio mediante diagrammi di Venn. Come sappiamo, ciò è
possibile per i casi n = 2; n = 3 e n = 4 :
Z
X
X
Y
X
Y
Y
Z
T
Eser cizio 1.89 Mostrare che l’identità ® = ¯ dove ® = x0 _y 0 e ¯ = (x ^y) 0
è valida.
Soluzione. Presi due insiemi liberi X; Y , abbiamo ® = ¯ se e solo se ® [X; Y ] =
c
¯ [X; Y ] ; cioè se e solo se (X c [ Y c ) = (X \ Y ) : Il ché vale:
52
da X c
eY c
X
Y
da X \ Y
X
X
Y
a X c [Y c
Y
a (X \ Y )c
;
X
Y
.
X
Y
E ser cizio 1.90 Siano ® = x ^ (y _ z); ¯ = (x _ y) ^ (x _ z) e ° =
(x ^ y) _ (x ^ z): Impiegando un diagramma con tre insiemi liberi dimostrare
la validità di ® = ¯ e la non validità di ® = °:
Soluzione.
Z
Z
X
Y
X \ (Y [ Z)
X
Z
Y
(X [ Y ) \ (X [ Z )
X
(X \ Y ) [ (X \ Z)
E ser cizio 1.91 Già sappiamo che i quattro insiemi del successivo diagramma a sinistra non sono liberi. Trovare due una identità che, pur non essendo
valida, è soddisfatta da tali insiemi.
t
x
Y
z
y
Soluzione. Nel diagramma vale X \ Y c \ Z \ T c = X c \ Y \ Z c \ T ,
dal momento che entrambe le espressioni denotano il vuoto. Questo mostra
perché generatori non liberi soddisfino delle identità non valide. Poiché ogni
espressione può esser posta in FNM, il punto di partenza è la verifica delle congiunzioni elementari. Per il Teorema 1.62, l’unico caso in cui l’interpretazione
di due diverse congiunzioni elementari può coincidere è che entrambe valgano
0, il che non capita mai per generatori liberi.
1.11 Anelli booleani
Definizione 1.92 Un anello commutativo unitario (A; +; ¢) con 0 6= 1 è booleano se, per ogni x 2 A, x ¢ x = x:
53
Teor ema 1.93
Sia (A; ^; _;0 ; 0; 1) un’algebra di Boole. Ponendo
x + y = (x ^ y 0 ) _ (x0 ^ y);
x¢y = x^y
(1.5)
abbiamo che la struttura (A; +; ¢) è un anello booleano, i cui 0 ed 1 sono quelli dell’algebra.
Dimostrazione. Per avere maggiore intuitività, impieghiamo per l’algebra di
Boole il linguaggio insiemistico (per il Teorema di Stone, ciò non è riduttivo). Sia dunque C un’algebra di insiemi su un universo U e sia x + y =
(x \ y c ) [ (xc \ y). Dimostriamo dapprima che (C; +) è un gruppo commutativo. L’operazione + è associativa. Infatti, per ogni x; y; z 2 C si ha:
(x + y ) + z = ((x \ y c) [ (xc \ y )) + z =
c
= (((x \ y c ) [ (xc \ y)) \ z c)[(((x \ y c ) [ (xc \ y)) \ z) = (riconducendo il termine in forma normale disgiuntiva)
c
= (x \ y c \ z c) [ (xc \ y \ z c ) [ ((x \ y)c \ (xc \ y)) \ z) =
= (x \ y c \ z c) [ (xc \ y \ z c ) [ ((xc [ y ) \ (x [ y c ) \ z) =
= (x\y c\z c )[(xc \y\z c )[(((xc \ x) [ (xc \ y c ) [ (y \ x) [ (y \ y c )) \ z) =
= (x \ y c \ z c) [ (xc \ y \ z c ) [ (xc \ y c \ z) [ (x \ y \ z):
Procedendo in modo analogo con x + (y + z) si perviene allo stesso risultato.
L’elemento neutro del gruppo è l’insieme vuoto ; (cioè lo 0 del gruppo coincide con lo 0 dell’algebra). Infatti ; + x = ((; \ xc) [ (;c \ x)) = ; [ x = x
per ogni x 2 C:
Per quanto riguarda l’opposto abbiamo, per ogni x 2 C; x + x = (x \ xc) [
(xc \ x) = ; [ ; = ;: Dunque ¡x = x (ogni elementi è autoinverso).
Infine, la somma è commutativa, poiché \ e [ lo sono.
Ora, nel gruppo (C; +) consideriamo come ulteriore operazione ¢ l’usuale interserzione insiemistica \, e dimostriamo che la terna (C; +; ¢) è un anello commutativo unitario.
L’intersezione è associativa. Vediamo la distributività. Siano x; y ; z 2 C: Si
ha:
x ¢ (y + z) = x \ ((y \ z c ) [ (y c \ z)) = (x \ y \ z c ) [ (x \ y c \ z).
Stesso risultato otteniamo partendo da x ¢ y + x ¢ z: Infatti x ¢ y + x ¢ z =
(x \ y) + (x \ z) =
c
c
= ((x \ y) \ (x \ z) ) [ ((x \ y ) \ (x \ z)) =
c
c
c
c
= (x \ y \ (x [ z )) [ ((x \ y ) \ x \ z) =
= (x \ y \ xc ) [ (x \ y \ z c) [ (xc \ x \ z) [ (y c \ x \ z ) =
= (x \ y \ z c ) [ (y c \ x \ z ) :
L’unità è data da U (cioè l’1 dell’anello coincide con l’1 dell’algebra) : Infatti,
per ogni x 2 C; si ha U \ x = x \ U = x: Ciò conclude la dimostrazione.
Vale anche il passaggio inverso, la cui dimostrazione, sostanzialmente analoga
alla precedente, non facciamo.
54
Teor ema 1.94
Sia (A; +; ¢) un anello booleano. Ponendo
x ^ y = x ¢ y;
x0 = 1 + x
x _ y = x + y + (x ¢ y);
(1.6)
abbiamo che la struttura (A; ^; _;0 ; 0; 1) è una algebra di Boole, il cui anello
booleano corrispondente (ottenuto tramite il Th.1.93) è (A; +; ¢)
Gli anelli booleani sono dunque tutti e soli quelli che si ottengono tramite il
Teorema 1.93. Poiché per ogni x 6= 1 non esiste y tale che x \ y = 1, nessun
anello booleano che contenga un elemento x diverso da 0 e da 1 è un campo, in
quanto A ¡ f0g non può essere un gruppo rispetto all’operazione di prodotto.
E sem pio 1.95 Consideriamo l’algebra di Boole di 4 elementi (A; _; ^;0 ; 0; 1)
dove A = f0; a; b; 1g (con b = a0 ). Applicando la conversione (1.5) otteniamo
la seguenti tabelle per le operazioni + e ¢ (trattandosi di operazioni commutative possiamo riempire solo metà matrice) :
+
0
a
b
1
0
0
a
a
0
b
b
1
0
1
1
b
a
0
¢
0
a
b
1
0
0
a
0
a
b
0
0
b
1
0
a
b
1
Il Teorema 1.93 ci dice che la struttura (A; +; ¢) è un anello booleano. Ora,
applicando la conversione (1.6) su (A; +; ¢), otteniamo
_
0
a
b
1
0
0
a
a
a
b
b
1
b
1
1
1
1
1
^
0
a
b
1
0
0
a
0
a
b
0
0
b
1
0
a
b
1
0
1
b
a
0
0
a
b
1
cioè l’algebra di Boole (A; _; ^;0 ; 0; 1) da cui siamo partiti.
Vediamo ora di caratterizzare gli anelli booleani finiti. Sappiamo che, dato un
numero m, se m non è una potenza di 2 non vi è alcuna algebra di Boole avente
m elementi, mentre se m è una potenza di 2, allora (a meno di isomorfismi) ne
esiste una ed una sola. Quindi, per la corrispondenza dimostrata, avremo un
solo anello booleano per ogni potenza di 2, e nessuno altrimenti.
Consideriamo l’algebra di Boole di 2 elementi 2 = (B; ^; _;0 ; 0; 1) dove B =
^ 0 1
_ 0
f0; 1g e le operazioni sono descritte dalle seguenti tabelle: 0 0 0 ; 0 0
1 0 1
1 1
1
1 ; 1
1
0
0
0 :
1
55
L’anello booleano corripondente all’algebra 2 è Z2: Infatti dalle trasformazioni
¢ 0 1
+ 0 1
x+y = (x ^ y 0)_(x0 ^y ) e x¢y = x^y otteniamo 0 0 0 e 0 0 1 :
1 0 1
1 1 0
n
Consideriamo ora l’algebra di Boole di 2 elementi facendo il pr odotto diretto
2 £ 2 £ ::: £ 2 n-volte, cioè consideriamo l’algebra (B; ^; _;0 ; 0; 1) dove
n
B = f0; 1g = f(c1; :::; cn) : ci = 0 o ci = 1g
(c1; :::; cn) ^ (d1 ; :::; d n) = (c1 ^ d1; :::; cn ^ dn )
(c1; :::; cn) _ (d1 ; :::; d n) = (c1 _ d1; :::; cn _ dn )
(c1; :::; cn)0 = (c01; :::; c0n): (si osservi come la definizione di prodotto diretto
tra algebre sia equivalente a quella tra gruppi).
Tale algebra viene indicata con 2n :
Ovviamente, poiché le operazioni sono definite per componenti e poiché l’algebra 2 corrisponde all’anello Z2, avremo che l’anello corripondente a 2n sarà
n
(Z2) , cioè il prodotto diretto di Z 2 £ ::: £ Z2 : Gli unici anelli booleani finiti
sono dunque i prodotti diretti di Z2 :
Riferendoci ai campi di insiemi, ci chiediamo che cosa corrisponda in tale contesto all’operazione +. Dati x e y abbiamo:
x + y = (x ^ y 0 ) _ (x0 ^ y) = (x \ y c ) [ (xc \ y):
Tale elemento prende il nome di differ enza sim metr ica di x e y, poiché (x \ y c )[
(xc \ y) è uguale (x ¡ y ) [ (y ¡ x); ed è sovente indicato con x © y . Vale
anche x © y = x [ y ¡ (x \ y) e x © y = (x [ y ) \ (x \ y) c
Se consideriamo le algebre di Boole F e F n ottenute dalla logica proposizionale, abbiamo
¡
0 ¢ ¡
0¢
[']n + [Ã]n = [']n ^ [Ã]n _ [Ã]n ^ [']n = [(' ^ :Ã) _ (:Ã ^ ')]n :
La formula (' ^ :Ã)_(:à ^ ') è vera quando una ed una sola tra ' e à è vera.
Sovente si introduce un nuovo connettivo, detto disgiunzione for te (o XO R)
¹ ; al quale è attribuita la tavola di verità di (' ^ :Ã) _
e simbolizzato con _
¹ Ã]n.
(:Ã ^ '). In tal modo, [']n + [Ã]n = ['_
¹Ã
' Ã
'_
0 0
0
¹Ã
² disgiunzione forte: '_
0 1
1
1 0
1
1 1
0
Riassumiamo le corrispondenze trovate:
negli anelli booleani:
somma +
j
j
nei campi di insiemi:
differenza simmetrica ©
j
j
in logica proposizionale:
¹
disgiunzione forte _