Dipartimento di Fisica
Scuola di Specializzazione in
Fisica Medica
A.A. 2012/2013
Statistica nelle applicazioni
sanitarie
Maria Roberta Monge:
[email protected]
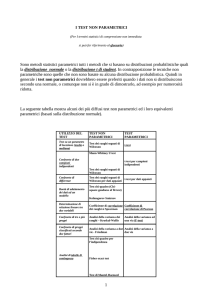
Test parametrici e non parametrici
• I test statistici si dividono in due diverse tipologie,
i test parametrici ed i test non parametrici.
• Si parla di test parametrici quando si suppone
nota la distribuzione di probabilità della v.a.
studiata per cui l’inferenza si riferisce solo ai
parametri che la caratterizzano. Si possono
effettuare test parametrici anche quando si ha
una conoscenza solo parziale della distribuzione,
ad esempio la sua caratteristica asintotica.
• Si parla invece di test non parametrici
quando la verifica viene fatta senza fare
alcuna assunzione stringente sulla
distribuzione della v.a. studiata per cui
l’inferenza può riguardare sia la forma
della distribuzione, sia i suoi parametri
(distribution free).
• Occorre però osservare che è comunque
necessaria una conoscenza minimale
della funzione di ripartizione (o funzione
cumulativa) della v.a. sottoposta al test.
Verifiche d’ipotesi
Test parametrici
Forma nota (tipicamente:
X~N(μ,σ2)
Inferenza su una
singola popolazione:
test sul valor medio,
test sulla varianza,
test sulle proporzioni
Test non parametrici
Test di
bontà
dell’adattamento
Inferenza su due
popolazioni:
test sulle differenze
di valori medi,
di proporzioni,
su campioni appaiati
Test di
confronto
fra due campioni
Test parametrici
• Si assume nota la forma della popolazione
considerata.
• Le inferenze si fanno sui parametri.
• Tipicamente si applicano a popolazioni
normali o approssimativamente normali.
• A seconda del parametro che si testa e
della conoscenza degli altri parametri
vengono utilizzate le statistiche normale,
di Student e di Helmert (χ2).
Test su campioni appaiati o prove
ripetute
• Sono test parametrici che riguardano quelle analisi
in cui occorra verificare la variazione di un
parametro, tipicamente il valore medio, di un unico
campione in tempi diversi (prima e dopo un certo
avvenimento, prima e dopo un certo trattamento
medico, prima e dopo un certo addestramento,
etc.)
• Nei test sulle differenze di valori medi o proporzioni
i due campioni considerati sono assunti
indipendenti tra loro e quindi il confronto è tra due
v.a. indipendenti X e Y. In questo caso invece le
due v.a. X e Y che descrivono il “prima” e il “dopo”
non sono tra loro indipendenti in quanto sono
associate alla stessa unità statistica.
• Non è pertanto possibile utilizzare l’usuale
test sulle differenze che presuppone che i
due campioni siano indipendenti tra loro.
• In questo caso tuttavia è possibile utilizzare
la variabile aleatoria “differenza”
D=X-Y
• Le realizzazioni di = xi –yi di questa v.a.
risultano infatti tutte indipendenti tra loro
come le realizzazioni di una singola v.a..
• La verifica d’ipotesi si riduce quindi ad un test sul
valore medio con varianza incognita con le
seguenti ipotesi statistiche:
H 0 : E (D ) = 0
H1 : E (D ) ≠ 0 oppure > o < 0
• La test-statistica risulta quindi una distribuzione di
Student con υ = n-1 gradi di libertà se le
osservazioni sono n ed X e Y possono essere
assunte normali o approssimativamente normali.
Test non parametrici
• Queste verifiche d’ipotesi non partono da
assunzioni fatte sulla possibile distribuzione che
descrive le osservazioni (distribution free).
• Sono pertanto utili in tutti i casi in cui:
¾Si voglia verificare anche il tipo di
distribuzione tipica delle osservazioni
effettuate (test di bontà dell’adattamento).
¾Non si possa assumere che la
distribuzione dei valori osservati sia nota e
assuma forma normale.
Test di bontà dell’adattamento
• Quando il problema che ci si pone è un
problema di bontà dell’adattamento, cioè
di come delle osservazioni o delle misure
si adattino ad un modello probabilistico di
distribuzione nota che si ipotizza per esse,
il test non parametrico più utilizzato è il
test di significatività del χ2 . In questo caso
la verifica riguarda l’intera distribuzione
della variabile aleatoria considerata.
• Esso viene utilizzato sia per v.a. continue
sia per v.a. discrete.
• Abbiamo visto inoltre che può essere
utilizzato quando si considerano v.a.
qualitative come verifica di indipendenza tra
caratteri o di omogeneità tra due campioni
(tabelle di contingenza). La distribuzione di
Helmert può essere utilizzata per
quantificare la bontà dell’adattamento se i
campioni sono sufficientemente numerosi in
quanto la statistica utilizzata tende
asintoticamente a questa distribuzione.
Test di Kolmogorov
• Un altro test di bontà dell’adattamento
molto utilizzato quando si hanno v.a.
continue è il test di Kolmogorov che, invece
di utilizzare il confronto tra le frequenze
osservate ed attese nelle diverse classi,
utilizza il massimo della differenza assoluta
fra la funzione di ripartizione (funzione
cumulativa) osservata e quella teorica
specificata dall’ipotesi nulla H0 .
• In questo caso l’ipotesi formulata è
H 0 : F ( x ; ϑ ) = F0 ( x )
Si calcola la funzione di ripartizione sperimentale
Fn ( x ) e, se è vera H0 , Fn ( x ) → F0 ( x ) e la
differenza fra funzione sperimentale e teorica
sarà minima.
• Si utilizza quindi come test-statistica
Dn = sup Fn ( x ) − F0 ( x )
e si può dimostrare che la sua distribuzione è
indipendente dalla distribuzione di X ~ F0 ( x ; ϑ )
specificata nell’ipotesi nulla, purchè essa sia
continua, per cui il test risulta non parametrico.
• Il calcolo esatto della funzione di
ripartizione della statistica Dn è possibile,
ma diventa dispendioso al crescere di n
per cui Kolmogorov e Smirnoff hanno
valutato la distribuzione asintotica, già
valida per n≥35 a partire dalla quale si
possono costruire apposite tabelle.
Test di confronto fra due campioni
• Anche nel caso dei test non parametrici, l’ipotesi
di fondo che si esprime con l’ipotesi nulla è che i
due campioni provengano dalla stessa
popolazione di cui però non si hanno
informazioni dettagliate sulla distribuzione ma
solo una conoscenza parziale della v.a. che la
descrive, in particolare la sua natura (discreta o
continua) e l’andamento della sua funzione di
ripartizione.
• In base all’ipotesi nulla si testa, come nel caso
dei test parametrici, se la v.a. differenza abbia o
meno valore atteso nullo, utilizzando indicatori
diversi dai parametri della popolazione.
• Solitamente questi test verificano l’ipotesi su un
indice di posizione della distribuzione e
tipicamente utilizzano come indicatore la
mediana.
• Infatti, partendo dalla considerazione che, per
qualsiasi v.a. X per definizione di mediana Me si
ha
1
P( X ≥ Me ) = P( X ≤ Me ) =
2
risulta più semplice, utilizzando la distribuzione
binomiale con parametro 0.5, derivare per la teststatistica una distribuzione “libera” da parametri
della popolazione da cui il campione viene
estratto.
• Alternativamente si utilizzano le v.a. rango
(rank) definite come l’intero corrispondente al
posto occupato dalla realizzazione della v.a.
Xi una volta che la sequenza campionaria sia
ordinata in senso crescente. La v.a. rango
per un campione casuale di dimensione n
costituisce una permutazione casuale degli
interi (1,2,…,n). Poiché tutte queste n!
permutazioni sono equiprobabili, è possibile
determinare il valore atteso delle v.a. rango.
Test dei segni
• Si utilizza per verificare se due campioni
provengono dalla stessa popolazione o in
alternativa per verificare, a partire da un unico
campione, un’ipotesi sul valore della mediana
della popolazione.
• Nel primo caso si vuole verificare se la mediana
della v.a. differenza sia nulla. Nel secondo si
verifica l’ipotesi che la mediana della
osservazioni sia compatibile con il valore
ipotizzato.
• In entrambi i casi il test si riconduce ad
utilizzare valori critici che provengono
dalla distribuzione binomiale in quanto si
vanno a determinare il numero di
osservazioni Xi con valore superiore alla
mediana ipotizzata o in cui la differenza
Di = Xi –Yi risulta maggiore di zero.
Questo numero di osservazioni risulterà
essere una v.a. Tn distribuita secondo una
binomiale con parametri n, numero di
osservazioni e p, probabilità di avere Xi >
mediana ipotizzata o Di >0.
• Ne segue che le ipotesi iniziali nel caso di un
singolo campione
H 0 : Me( X ) = Me0
H1 : Me( X ) ≠ Me0
si riformulano come
1
H0 : p =
2
1
H1 : p ≠
2
in quanto T n ~ Bin (n , p )
da cui la regione critica si determinerà come
α⎞
n
⎛
Tn − ≥ tc ⎜ ⎟
2
⎝2⎠
• Analogamente, nel caso di due campioni, le
ipotesi
H 0 : Me(Di = X i − Yi ) = 0
H1 : Me(Di = X i − Yi ) ≠ 0
si riformulano come nel caso precedente.
• Questa procedura inferenziale viene detta test
dei segni in quanto solitamente si indicano con +
le osservazioni che superano la mediana
considerata e con – quelle che non la superano o
viceversa e si contano quindi i segni positivi.
• Solitamente questo test nel caso di due campioni
si utilizza per campioni appaiati o prove ripetute
in quanto i due campioni devono avere la stessa
numerosità.
• Se si ottengono valori di Xi ed Yi coincidenti, per
cui la differenza risulta nulla, viene suggerito di
escludere tali valori dall’analisi in quanto
modificano il livello di significatività del test.
• Il motivo è che, se X e Y sono v.a. continue, la
probabilità che si verifichino valori coincidenti è
nulla: in pratica però nel campionamento questo
può succedere.
• L’analisi dei valori coincidenti va comunque
curata con molta attenzione perché le probabilità
di errore possono modificarsi sensibilmente.
Test dei ranghi con segno di
Wilcoxon
• Anche questo test può essere utilizzato sia
per verificare se un unico campione
possieda una mediana prefissata Me0 o se
le differenze di campioni appaiati abbiano
mediana pari a zero.
• Come il precedente è quindi l’equivalente
non parametrico del test t di Student
quando si tratta test sulla mediana anziché
sul valor medio o di campioni appaiati ed è
con esso che va confrontato.
• Si considerano in entrambi i casi le
differenze Di = Xi – Me0 oppure Di = Xi – Yi
nel caso di campioni appaiati.
• Si assume che le v.a. Di siano tutte
indipendenti tra loro, simmetriche, continue e
con la stessa mediana.
• Si considerano tutte le Di non nulle e si
attribuiscono loro i ranghi da 1 a n dopo
averle ordinate in senso crescente da min|Di|
a max|Di|.
• In caso di ranghi coincidenti di utilizza la
media aritmetica dei ranghi.
• L’ipotesi nulla da verificare è
H 0 : Me(Di ) = 0
contro le possibili ipotesi alternative
bidirezionale o unidirezionali.
• La test-statistica dei ranghi con segno di
Wilcoxon è la somma dei ranghi corrispondenti
alle differenze Di >0:
n
Tn = ∑ r ( Di ) I (Di > 0 )
i =1
dove I è la funzione indicatrice che vale 1
oppure 0 a seconda che Di > 0 sia vero o
falso.
• Si dimostra che
n(n + 1)
n(n + 1)(2n + 1)
E (Tn ) =
; Var (Tn ) =
4
24
• I valori critici sono tabulati per piccoli valori di n.
• Già per n>15 si può ricorrere alla
approssimazione normale per la validità del
teorema del limite centrale poiché la v.a. Tn è
definita come somma di v.a. indipendenti e
simili e sotto l’ipotesi nulla risulta simmetrica
attorno al valor medio, per cui la corrispondente
v.a centrata ridotta, modificata per la correzione
di continuità (approssimazione per interi), tende
alla normale standard.
Test U di Mann Whitney
• Questo test è stato proposto da Mann e Whitney
per il confronto fra campioni di numerosità
diversa ed è collegato ad un test analogo
proposto da Wilcoxon per campioni appaiati o di
pari numerosità (Wilcoxon sum rank test).
• Si considerano due campioni casuali di
numerosità diversa (X1,X2 ,…,Xi ,…,Xn) e
(Y1,Y2 ,…,Yj ,…,Ym) provenienti da due
popolazioni X e Y.
• Si vuole verificare se i due campioni provengano
dalla stessa popolazione cioè se X≡Y.
• L’ipotesi nulla sarà
H 0 : FX (u ) ≡ FY (u ) ∀u
(dove F rappresenta la funzione di ripartizione
delle due popolazioni X e Y) contro le usuali
ipotesi alternative bidirezionale e monodirezionale
destra e sinistra.
• Si considera un unico campione combinato ed
ordinato di m+n elementi, ottenuto dalle
osservazioni di X e Y ordinate in senso crescente.
• Si costruiscono le seguenti v.a. per definire la
test-statistica:
⎧1 se Y j < X i
Dij = ⎨
⎩0 se Y j > X i
∀ i = 1,2,..., n ; j = 1,2,..., m
• Si definisce la test-statistica U di Mann e Whitney
n
m
U = ∑∑ Dij
i =1 j =1
Essa rappresenta il numero di volte che Y
precede X nel campione combinato ed ordinato
e, poichè si ha
p = P(Y < X ) =
∞ x
∫ ∫ f ( y)f
Y
−∞ −∞
∞
X
( x )dydx = ∫ FY ( x ) f X ( x )dx
−∞
se è vera l’ipotesi nulla f X (u ) ≡ fY (u ) ,
la probabilità p sopra riportata vale ½.
Le Dij sono allora v.a. di Bernoulli e quindi, se è
vera l’ipotesi nulla, U è la somma di mn v.a.
bernoulliane con parametro p=1/2.
• Quindi, se è vera H0, si avrà
mn
mn(m + n + 1)
E (U ) =
; Var (U ) =
12
2
Nel ricavare le espressioni riportate sopra,
occorre tenere conto che le Dij non sono
indipendenti tra loro, per cui il valore atteso della
somma sarà la somma dei valori attesi, ma
questo non vale per la varianza il cui calcolo
risulta pertanto un po’ più complesso.
• Per il teorema del limite centrale la v.a. centrata
ridotta che si ottiene da U, modificata per la
correzione di continuità, tende alla normale
standardizzata.
Test W di Wilcoxon della somma
dei ranghi
• Come abbiamo già detto, questo test è l’analogo
del precedente, che ne è la generalizzazione,
nel caso di campioni di stessa numerosità.
• Si basa sulla considerazione che, date due
popolazioni X e Y, se la mediana MeX di X
supera la mediana MeY di Y, allora i ranghi del
campione combinato e ordinato delle unità
statistiche provenienti da X saranno
prevalentemente superiori ai ranghi delle unità
provenienti da Y.
• Si testerà pertanto l’ipotesi nulla
H 0 : Me X − MeY = 0
contro le usuali ipotesi alternative bidirezionale o
monodirezionali destra o sinistra.
• Si utilizza la test-statistica W di Wilcoxon definita
come
n
n+m
W = ∑ r ( X i ) = ∑ iQi
i =1
i =1
dove r ( X i ) è il rango che compete ad Xi nel
campione combinato ed ordinato e Qi è una v.a.
così definita:
⎧1 se l' elemento i − esimo proviene da X
Qi = ⎨
per i = 1,2,...n + m
⎩0 se l' elemento i − esimo proviene da Y
• La distribuzione di W varia tra n(n + 1) / 2 quando
tutti gli elementi di X sono nei primi n posti (ed
allora W = 1 + 2 + ... + n ) a mn + n(n + 1) / 2 quando
gli elementi di X sono agli ultimi n posti (ed
allora W = (m + 1) + (m + 2 ) + ...(m + n ) ).
• La distribuzione di W risulta simmetrica rispetto
al suo valore atteso e si ha
n(m + n + 1)
mn(m + n + 1)
E (W ) =
; Var (W ) =
2
12
• Inoltre la distribuzione di W già per campioni di
numerosità >12 può essere sostituita dalla teststatistica centrata ridotta, modificata per la
correzione di continuità
Tn ,m
W − E (W ) − 0.5
=
σ (W )
che tende asintoticamente alla normale
standardizzata N(0,1).
Test di Kolmogorov-Smirnoff
• Un altro test non parametrico per verificare
se due campioni di diversa numerosità
provengano dalla stessa popolazione è il
test di Kolmogorov-Smirnoff.
• Si applica quando si hanno due campioni
casuali indipendenti, rispettivamente di
numerosità n e m.
• Non è pertanto applicabile a campioni
appaiati.
• Si formula l’ipotesi nulla
H 0 : FX ( w) ≡ GY ( w) ∀w
contro l’ipotesi alternativa
H1 : FX ( w) ≠ GY ( w) per almeno un w
dove le F rappresentano le funzioni di ripartizione
di X e Y rispettivamente.
• Si calcolano per entrambi i campioni le funzioni di
ripartizione sperimentali Fn ( w) e Fm ( w) .
• Si costruisce la test-statistica
Dn = sup Fn ( w) − Gm ( w) ∀ − ∞ < w < ∞
• Per rifiutare l’ipotesi nulla si verifica se Dn > dα ,n ,m
dove dα , n , m è il valore critico per il livello di
significatività α.
• I valori critici sono tabulati per piccoli valori di n e
m.
• Smirnoff ha dimostrato anche l’approssimazione
asintotica della distribuzione campionaria della
test-statisitica che è calcolabile in modo esatto
ma complicata.
• Limitando lo sviluppo in serie al primo ordine, si
ottiene che i valori critici asintotici valgono
1 ⎛ 1 1 ⎞ ⎛α ⎞
dα ,n ,m ≅ − ⎜ + ⎟log ⎜ ⎟
2⎝ n m⎠ ⎝ 2 ⎠