EFFETTO HALL
Mario Gervasio, Marisa Michelini, Lorenzo Santi
Unità di Ricerca in Didattica della Fisica, Università di Udine
Obiettivi: Misurare il coefficiente di Hall su campioni metallici ed a semiconduttore. Determinare il
segno ed il numero dei portatori liberi e la mobilità di deriva degli stessi.
Il modello classico (a gas di elettroni liberi) considera gli elettroni di valenza come un gas di particelle che si muovono in maniera disordinata all’interno del reticolo cristallino del metallo.
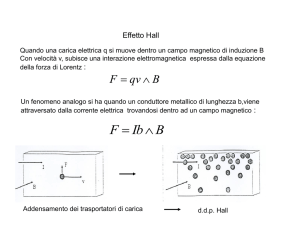
Prendiamo in considerazione un campione
(uno strato di materiale di forma parallelepipeda) come indicato in Figura 1,
immerso in un campo magnetico uniforme
di intensità B e diretto secondo l’asse z.
Si fa passare una corrente di intensità Ix
diretta lungo l’asse delle x.
Gli elettroni, sotto l’effetto del campo elettrico Ex, acquistano una velocità di deriva
v nel verso contrario al campo elettrico.
Essi risultano pertanto sottoposti alla forza
di Lorentz FL = q · v · B diretta lungo Figura 1. Geometria dell’effetto Hall.
l’asse delle y negative e tendono quindi
ad accumularsi sulla faccia del campione perpendicolare all’asse y e posta verso chi guarda la figura.
Questo accumulo di cariche determina una differenza di potenziale VH tra le due facce del campione
perpendicolari all’asse y. Il campo elettrico EH che si viene a generare (campo di Hall) determina
una forza elettrica q · EH uguale ed opposta alla forza di Lorentz nei termini che EH = v · B dalla
quale si evidenzia che il campo di Hall è direttamente proporzionale sia al campo magnetico B che
alla velocità di deriva v.
Si definisce il coefficiente di Hall come RH = EH /(Jx · B) dove EH = v · B. Ricordando che
Jx = Ix / a · s = q · n · v si ottiene
RH = v B / (q · n · v B) = 1/ q · n = - 1/ e · n
(1.1)
quindi la misura di RH ci permette di conoscere la concentrazione n dei portatori liberi.
La misura della conducibilità elettrica , associata alla misura di RH ci permette inoltre di conoscere
la mobilità di deriva !, definita come rapporto tra la velocità di deriva v ed il campo elettrico Ex
RH
= RH (Jx / Ex) = 1/ q · n (q · n · v · ! / v) = !
(1.2)
Per effettuare la misura del coefficiente di Hall è necessario misurare VH, Ix, B e lo spessore del campione s, in quanto RH = EH / (Jx · B) dove EH = VH / a e Jx = Ix / a · s e pertanto
RH = VH · s / (Ix · B)
(1.3)
Misura su campioni metallici
L’ordine di grandezza di RH per i metalli più comuni è dell’ordine di 10-11 m3 C-1 ed è chiaro che per
avere valori di VH misurabili occorrerà utilizzare un campo magnetico sufficientemente intenso (un
valore facilmente ottenibile è di 1 T), una corrente elevata (almeno 10 A) ed uno spessore del campione ridotto a qualche centesimo di millimetro.
Progetto IDIFO - Proposte didattiche sulla fisica moderna
195
Dalla relazione (1.3) si evince che, anche con spessori del campione di qualche micron, la tensione
di Hall VH risulterà dell’ordine di pochi microvolt e sarà quindi necessario l’utilizzo di un amplificatore con guadagno almeno 1.000 ed una altissima impedenza di ingresso.
Per la misura del campo magnetico B viene utilizzata una sonda ad induzione collegata ad un integratore di carica.
Per un campione di Rame di spessore 30 m, sottoposto ad un campo magnetico di 0,98 T, si sono
ottenuti i seguenti risultati:
Figura 2. tensione di Hall VH in funzione della corrente I per B = 0,98T.
L’interpolazione lineare dei dati ottenuti fornisce RH = - 5,8 · 10-11 m3/ C
In letteratura si trova. Lo scostamento da questo valore è dovuto principalmente alla incertezza data
dagli errori sullo spessore del campione e sul valore di B.
Dalla 1.1 si ricava che la concentrazione degli elettroni liberi n, col valore da noi ottenuto per RH è:
n = 1/(e · RH) = 1 / (1,6·10-19 · 5,8·10-11) = 10,8·1028 m-3
Il confronto di questo risultato con il valore della previsione teorica (n " 8,5·1028 m-3) conferma che
entro un margine di errore del 22 % la prova sperimentale conferma le previsioni del modello a gas
di elettroni liberi.
Le previsioni del modello a gas di elettroni liberi trovano conferma sperimentale per la tutti i metalli
del gruppo I della tabella di Mendeleev, ma non, ad esempio, per quelli del gruppo II. Questi metalli
hanno addirittura un valore di RH positivo come se i portatori liberi non fossero elettroni ma cariche positive.
I risultati ottenuti per un campione di Zinco di spessore 30 m, sottoposto ad un campo magnetico
di 0,99 T, sono evidenziati nella Figura 3.
Per poter spiegare queste anomalie occorre introdurre nuovi concetti, come la teoria delle bande di
energia per gli elettroni.
Il segno positivo di RH per questi metalli si spiega in quanto per essi la banda di valenza risulta essere
quasi piena. L’agitazione termica porta alcuni elettroni ad occupare i livelli più alti di tale banda e
quindi in essa rimangono presenti livelli energetici non occupati, ossia delle lacune che, sottoposte
all’azione del campo elettrico E si muovono, intuitivamente, nel verso del campo elettrico stesso
come fossero cariche positive.
196
Capitolo 3. Esperimenti
Figura 3. Tensione di Hall VH in funzione della corrente I per B = 0,99T.
Figura 4. Tensione di Hall VH in funzione della corrente I per B = 0,427 T.
Misura su campioni a semiconduttore
Le misure verranno effettuate su campioni di Ge con drogaggio sia di tipo P che di tipo N.
Il coefficiente di Hall dei semiconduttori è di molti ordini di grandezza inferiore a quello dei metalli,
dato il numero nettamente inferiore dei portatori liberi. L’esperimento richiede correnti di polarizzazione dei campioni dell’ordine dei mA per ottenere tensioni di Hall già dell’ordine dei mV.
Anche per i semiconduttori i risultati sperimentali evidenziano il fatto che il segno della tensione
di Hall non è sempre negativo e questo naturalmente mette in discussione il modello a gas di elettroni liberi.
Vi è inoltre una osservazione da fare e riguarda la deviazione dalla linearità che si riscontra per i
valori più elevati della corrente di polarizzazione. Ciò è dovuto al fatto che RH diminuisce al crescere della temperatura ed addirittura, nel semiconduttore di Ge drogato P, si riscontra l’inversione
Progetto IDIFO - Proposte didattiche sulla fisica moderna
197
Figura 5. Valore medio, sulle misure precedentemente effettuate, della tensione di Hall VH in
funzione della corrente I per B = 0,427 T.
del segno della tensione di Hall qualora si riscaldi con un phon il campione mentre si trova tra le
espansioni polari del magnete.
Le prove su un campione di GeP sono state effettuate introducendo il campione nel campo magnetico prima in un senso e poi ruotato di 180° (ciò equivale ad invertire la direzione di B).
In un secondo tempo si è fatta la media delle due letture (in modulo) e questo per annullare totalmente l’effetto della d.d.p. dovuta al non perfetto allineamento dei contatti trasversali del campione
su una linea equipotenziale.
In Figura 4 sono riportati i risultati ottenuti nelle due serie di letture ed in Figura 5 la media delle
misure effettuate.
Figura 5. Tensione di Hall VH in funzione della corrente I per B = 0,46 T.
198
Capitolo 3. Esperimenti
Dal fit del grafico otteniamo per RH il seguente valore:
RH = VH s / (Ix B) = (VH / Ix) · s /B = 3,02 ·10-2 m3/ C
Misurando anche la resistenza elettrica del campione, le sue dimensioni e calcolandone quindi la resistività si può anche calcolare la mobilità di Hall (per questo campione #=15 $ cm):
! H = RH / # = 0,201 m2V-1s-1
La mobilità di Hall, per campioni di Ge fortemente drogati, deve risultare circa uguale alla mobilità
di deriva (3900 cm2V-1s-1 per gli elettroni e 1900 cm2V-1s-1 per le lacune)
La concentrazione dei portatori liberi (nel nostro caso lacune) risulta p = 2,1 ·1020 m-3
I risultati ottenuti per un campione di GeN dello spessore di 1,65 mm sottoposto ad un campo magnetico di 0,46 T sono riportati in Figura 5.
Dal fit del grafico otteniamo per RH il seguente valore:
RH = VH s / (Ix B) = (VH / Ix) · s /B = - 3,23 ·10-3 m3/ C