calcolo delle distanze di mappa

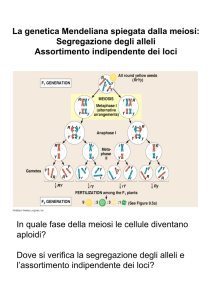
RB

CALCOLO DELLE DISTANZE DI MAPPA
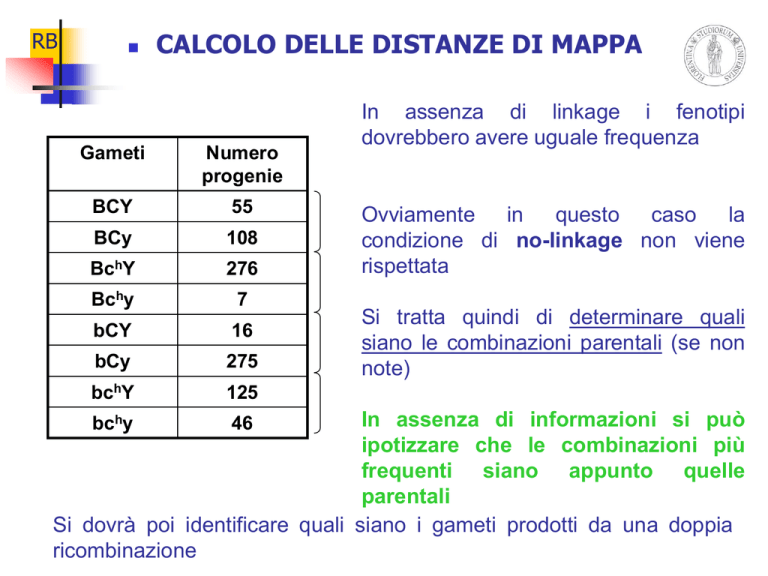
Gameti
Numero
progenie
BCY
55
BCy
108
BchY
276
Bchy
7
bCY
16
bCy
275
bchY
125
In assenza di linkage i fenotipi
dovrebbero avere uguale frequenza
Ovviamente in questo caso la
condizione di no-linkage non viene
rispettata
Si tratta quindi di determinare quali
siano le combinazioni parentali (se non
note)
In assenza di informazioni si può
ipotizzare che le combinazioni più
frequenti siano appunto quelle
parentali
Si dovrà poi identificare quali siano i gameti prodotti da una doppia
ricombinazione
bchy
46
RB
CALCOLO DELLE DISTANZE DI MAPPA
Gameti
Numero
progenie
BCY
55
BCy
108
BchY
276
Bchy
7
bCY
16
bCy
275
bchY
125
bchy
46
Le due forme evidenziate potrebbero
essere appunto dei doppi crossing
Mettendo insieme questa informazione con la conoscenza dei genotipi
parentali si può ipotizzare l’ordine dei loci sul cromosoma
CALCOLO DELLE DISTANZE DI MAPPA
RB
Vediamo un esempio:
A
b
C
c
a
B
c
b
C
A
B
c
B
c
a
b
C
A
b
C
a
B
A
x
a
A
b
C
x
a
B
c
NO CROSSING
SINGLE CROSSING
SINGLE CROSSING
A
b
c
a
B
C
CALCOLO DELLE DISTANZE DI MAPPA
RB
A
b
x
a
C
x
B
DOUBLE CROSSING
c
A
B
C
a
b
c
Il locus centrale si ricombina con gli altri due
I nostri dati reali mostrano che le combinazioni parentali
BchY
bCy
diventano
Bchy
bCY
I loci che rimangono insieme sono quindi
Bch
bC
E quindi il locus intermedio è Y/y
Ordine corretto degli alleli sui cromosomi parentali: BYch
byC
RB
CALCOLO DELLE DISTANZE DI MAPPA
Va ora calcolata la distanza tra loci
Si computerà la distanza tra B e Y e quella tra Y e C
Si usa il numero di ricombinanti tra loci
Le combinazioni parentali per B e Y sono BY e by
quindi By e bY sono ricombinanti e vanno considerati
n. = 108 + 7 + 16 + 125 = 256
(256 / 908) * 100 = 28,19 %
La distanza stimata tra questi loci è quindi 28,19 unità di mappa
CALCOLO DELLE DISTANZE DI MAPPA
RB
Similarmente
Per il secondo gruppo di loci Ych e yC avremo:
n. = 55 + 16 + 7 + 46 = 124
(124 / 908) * 100 = 13,66 %
La distanza stimata tra questi loci è quindi 13,66 unità di mappa
La mappa appare come:
28,19
B
13,66
Y
ch
RB
CALCOLO DELLE DISTANZE DI MAPPA
Se si esclude il locus Y il calcolo della distanza tra B e C si può basare su
Bch e bC
Avremo in questo caso:
n. = 55 + 108 + 125 + 46 = 334
(334 / 908) * 100 = 36,78 %
Che non è uguale alla somma di 28,19 + 13,66 = 41,85
La discrepanza è dovuta ai doppi crossing over di cui non si è tenuto conto
Il calcolo deve quindi comprendere i 23 doppi ricombinanti per due volte
dato che la distanza di mappa è basata sul numero di eventi di
ricombinazione
n. = 233 + 101 + 2(16+7) = 380
RB
CALCOLO DELLE DISTANZE DI MAPPA
(380 / 908) * 100 = 41,85 %
Che è uguale alla somma di 28,19 + 13,66 = 41,85
233 = 125 + 108  single crossing tra b e y
101 = 55 + 46  single crossing tra y e c
23 = 7 + 16  double crossing
combinazioni parentali
BYch
byC
Gameti
Numero
progenie
BYC
55
ByC
108
BYch
276
Bych
7
bYC
16
byC
275
bYch
125
bych
46
Se due loci sono più distanti di 50 unità di mappa (50% di ricombinazione) la
probabilità di crossing over è così elevata che i geni ai due loci sono sostanzialmente
unlinked e quindi segregano indipendentemente
RB
Ricapitoliamo ….
Il calcolo delle distanze è fondamentale per posizionare i
nostri marcatori sul genoma!!!
Gli esperimenti come quello visto prima non sempre sono
realizzabili
La possibilità di avere dei CROSSING OVER non visti sussiste
sempre
RB
Due geni che mappano sullo
stesso cromosoma si dicono
SINTENICI
Due
geni
sintenici
segregherebbero
sempre
assieme se non esistesse il
crossing-over nella prima
divisione meiotica
L’evento di crossing-over da
luogo alla formazione di
gameti RICOMBINANTI
RB
Il crossing-over separerà raramente loci che si trovano molto
vicini sullo stesso cromosoma, in quanto un solo evento di
crossing-over localizzato esattamente nel piccolo spazio tra i
due loci creerà dei ricombinanti
Più due loci sono distanti, più e’ probabile che un evento di
crossing-over li separi
Si definisce un valore detto frazione di ricombinazione,
misura della distanza di due loci
RB
 Determinare la frequenza con cui due loci ricombinano fra loro alla meiosi
= TETHA (
•
se due loci sono su cromosomi diversi segregano indipendentemente.
La probabilità che vengano ereditati insieme è del 1/2   = 50%
•
Se due loci sono vicini fra loro sullo stesso cromosoma saranno ereditati
insieme più frequentemente   < 50%
Tanto più sono vicini, tanto più piccola è la probabilità che avvenga un
crossing-over
LA FREQUENZA DI RICOMBINAZIONE () E’ UNA MISURA DELLA DISTANZA
GENETICA
RB
LE COSE SONO UN PO’ PIU’ COMPLICATE ….
Dopo una certa distanza fisica la frazione di
ricombinazione non rispecchia più la distanza genetica per
l’esistenza di doppi crossing-over
Loci che distano su una mappa 40 cM hanno una
ricombinazione molto inferiore al 40%, in quanto la
frazione di ricombinazione non supera mai lo 0,5
La frazione di ricombinazione sarà uguale a 0,5 non solo
per loci non sintenici, ma anche per loci sintenici molto
distanti fra loro
RB
Studiando quindi le meiosi o comunque le
ricombinazioni avvenute è necessario tener
conto di questi eventi non visibili
LE FUNZIONI DI MAPPA
definiscono le relazioni tra funzione di ricombinazione e
distanza genetica
RB
DISTANZA TRA GENI O LOCI
Abbiamo visto che la distanza tra geni si definisce:
DISTANZA DI MAPPA  (d)
d è funzione della frequenza di ricombinazione 
La relazione che lega queste due quantità è detta funzione di mappa
La più semplice funzione di mappa è d= 
Questa funzione assume una completa interferenza ( = 1)
Se si verifica un crossing-over in un cromosoma questo evento interferisce
totalmente con la possibilità che se ne verifichi un altro
RB
DISTANZA TRA GENI O LOCI
In realtà sono possibili più crossing over sullo stesso cromosoma
• dobbiamo utilizzare una funzione di mappa più complessa
• dobbiamo considerare  come la probabilità che in un dato intervallo si
verifichi un numero dispari di crossing-over (se infatti ne avviene un
numero pari non osserveremo alcuna ricombinazione)
• di conseguenza (1 – ) è la probabilità che si verifichi un numero pari
(zero incluso) di crossing over
RB
Esempio:
 AB = 0,20
A
 BC = 0,15
B
C
Supponiamo di tipizzare un individuo ABC/abc:
Aplotipi trasmissibili
Aplotipi visibili tipizzando solo i loci A e C
ABC e abc
AC e ac
Parentali
ABc e abC
Ac e aC
Ricombinanti
Abc e aBC
Ac e aC
Ricombinanti
AbC e aBc
AC e ac
Parentali
In realtà i parentali nascondono insieme ai veri parentali anche i doppi ricombinanti
(AbC e aBc)
RB
1   AC   1   AB 1   BC    AB  BC
La prob. che non si verifichi nessun crossing over (o un numero pari) tra A e C è
uguale alla probabilità che non si verifichi alcun crossing over (o un numero pari di
questi) tra A e B e tra B e C simultaneamente.
A questa probabilità va aggiunta quella che si verifichi simultaneamente un
crossing over (o un numero dispari di questi) tra A e B e tra B e C.
Dalla formula precedente e riassumendo:
 AC   AB   BC  2  AB  BC
RB
DISTANZA TRA GENI O LOCI
 AC   AB   BC  2  AB  BC
La formula implica che la probabilità di un doppio crossing over dipenda
dal semplice prodotto della probabilità degli eventi, considerati quindi
indipendenti.
Si assume quindi una totale mancanza di interferenza  = 0
Generalizzando:
 AC   AB   BC  2 1    AB  BC
Nell’esempio precedente assumendo  = 0 avremo:
AC = 0,20 + 0,15 – 2(0,20*0,15) = 0,29 a differenza di AC = 0,35 assumendo  = 1
Con valori di  piccoli (inferiori a 0,1) l’assunto di una completa interferenza può non
essere molto lontano dalla realtà e la funzione di mappa d =  è ragionevolmente
precisa.
RB
Sull’assunto dell’interferenza nulla è costruita la funzione di mappa di
Haldane
Haldane ha dimostrato che seguendo la distribuzione di Poisson si ottiene:
1
 2d 
   1  e


2
da cui
d 
1
2
ln 1  2  
Idealmente come abbiamo ricordato la distanza di mappa dovrebbe essere
additiva
(A-B)+(B-C)=(A-C)
Nell’esempio:
AB = 0,20
BC = 0,15
AC = 0,29
d = 0,255413
d = 0,178337
d = 0,433750
RB
DISTANZA TRA GENI O LOCI
Poisson  adatta  eventi rari in spazi o tempi grandi
Nel nostro caso il numero dei punti dove può avvenire un crossing over è
molto grande  100 cM = n (dimensione del campione)
La probabilità che avvenga nell’intervallo di 1 cM è molto piccola
 = 0,01 = 1%
La media della distribuzione è   = np = n = 100 * 0,01 = 1
Ossia 1 crossing over in 100 cM
In un intervallo di 1 cM esaminando molte meiosi, avremo eventi diversi
con probabilità descritte da:
P(x) = x * e- / x!
costante
RB
P(x) = x * e- / x!
Evento x
(n di X over)
e-

0
0,367879
1
1
1
0,367879
1
1
2
0,367879
1
2
3
0,367879
1
6
4
0,367879
1
24
5
0,367879
1
120
6
0,367879
1
720
7
0,367879
1
5040
8
0,367879
1
40320
9
0,367879
1
362880
10
0,367879
1
3628800
Totale
1–
P(x pari)
x!

P(x dispari)
Totale
0,3679
0,3679
0,1839
0,0613
0,0153
0,0031
0,0005
7,3E-05
9,1E-06
1,0E-06
1,0E-07
0,5677
0,4323
1
RB
Relazione tra theta e distanza di mappa
2,50
Distanza di mappa
(numero atteso di crossing over)
2,00
Haldane
1,50
1,00
Morgan
0,50
0,00
0
0,05
0,1
0,15
0,2
0,25
0,3
0,35
Frequenza di ricombinazione (theta)
0,4
0,45
0,5
0,43
Sommando tutte le meiosi in cui è avvenuto un numero dispari di crossing over
(ossia quelle che ci fanno vedere l’avvenuta ricombinazione) ne conteremo circa il 43%
Quindi quando  = 0,43
 d = 1 (Morgan)
DISTANZA TRA GENI O LOCI
RB
N.B.  la distanza di 1 cM corrisponde ad un numero di paia di basi molto
variabile da specie a specie (da 10 kb a 1000 kb).
Anche tra i sessi le distanze variano molto:
mammiferi  femmine maggiore distanza di mappa
Vi sono altre funzioni di mappa tra cui quella di Kosambi che assumono
valori di interferenza compresi tra 0 e 1
Kosambi suppone quindi che i crossing over non siano infiniti
cM 
1
4
ln
1  2
1  2

e
4 cM
2  e

4 cM
1
 1 

Sotto i 10 cM qualunque formula fornisce il risultato corretto
RB
DISTANZA TRA GENI O LOCI
Qual è la probabilità che un marcatore sia vicino ad un gene di interesse?
d = distanza da un marcatore
1 marcatore
L = lunghezza del genoma
P vicino
P non vicino
p= 2d/L
p=(1 – 2d/L)
p=(1 – 2d/L)m
m marcatori
Quindi la probabilità che sia vicino ad almeno 1 marcatore è:
2d 

p  1  1 

L


m
RB
DISTANZA TRA GENI O LOCI
Lunghezza del genoma mammiferi ~ 3000 cM
ESERCIZIO
L = 3000
m = 50
d = 20
p = ??
0,488
Ragionando al contrario 
m 
ln 1  p 
2d 

ln  1 

L 

Volendo una probabilità del 95% con i dati di prima
ci vogliono ~ 223 marcatori
Se vogliamo d = 5 con p = 0,95 ci vorranno ~ 900 marcatori