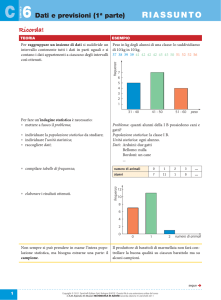
Michael C. Whitlock • Dolph Schluter
ANALISI STATISTICA
DEI DATI BIOLOGICI
Capitolo 16:
La correlazione tra variabili numeriche
M.C. Whitlock, Dolph Schluter, ANALISI STATISTICA DEI DATI BIOLOGICI, Zanichelli editore S.p.A. Copyright © 2010
16 | 1
M.C. Whitlock, Dolph Schluter, ANALISI STATISTICA DEI DATI BIOLOGICI, Zanichelli editore S.p.A. Copyright © 2010
16 | 2
M.C. Whitlock, Dolph Schluter, ANALISI STATISTICA DEI DATI BIOLOGICI, Zanichelli editore S.p.A. Copyright © 2010
16 | 3
Ricordo la definizione teorica di covarianza
Cov(X,Y) = E ( (X – µX)(Y-µY) )
e quella di correlazione
Cov(X, Y )
ρ(X, Y ) = �
V (X) · V (Y )
La covarianza (e quindi la correlazione)
viene stimata usando formule simili a
quelle usate per la varianza campionaria:
M.C. Whitlock, Dolph Schluter, ANALISI STATISTICA DEI DATI BIOLOGICI, Zanichelli editore S.p.A. Copyright © 2010
16 | 4
Correlation coefficient
Aim: establish and estimate association between two variables.
�n
(yi − ȳ )(zi − z̄)
�
Formula: rYZ = i=1
.
(Pearson’s)
(n − 1) SY2 SZ2
Property: −1 ≤ rYZ ≤ 1.
Confidence intervals and test of the hypothesis ρ = 0 use
assumption (Y , Z ) bivariate normal with correlation coefficient ρ.
If variables not normal, other coefficients used:
Kendall’s correlation coefficient τ use rank of observations, instead
of values.
Spearman’s correlation coefficient rS is also computed from ranks.
M.C. Whitlock, Dolph Schluter, ANALISI STATISTICA DEI DATI BIOLOGICI, Zanichelli editore S.p.A. Copyright © 2010
16 | 5
Esempi di dati corrispondenti a vari coefficienti di
correlazione.
M.C. Whitlock, Dolph Schluter, ANALISI STATISTICA DEI DATI BIOLOGICI, Zanichelli editore S.p.A. Copyright © 2010
16 | 6
Il coefficiente di correlazione stima le associazioni lineari
e non quelle non-lineari
M.C. Whitlock, Dolph Schluter, ANALISI STATISTICA DEI DATI BIOLOGICI, Zanichelli editore S.p.A. Copyright © 2010
16 | 7
M.C. Whitlock, Dolph Schluter, ANALISI STATISTICA DEI DATI BIOLOGICI, Zanichelli editore S.p.A. Copyright © 2010
16 | 8
Calcoli
r (Pearson) = 0.308
int.conf.95%: (0.02,0.55)
Test ρ = 0: P = 0.037
M.C. Whitlock, Dolph Schluter, ANALISI STATISTICA DEI DATI BIOLOGICI, Zanichelli editore S.p.A. Copyright © 2010
16 | 9
In forma grafica, l’ipotesi di distribuzione normale
bivariata usata nel test di correlazione
M.C. Whitlock, Dolph Schluter, ANALISI STATISTICA DEI DATI BIOLOGICI, Zanichelli editore S.p.A. Copyright © 2010
16 | 10
Possibili violazioni delle ipotesi
M.C. Whitlock, Dolph Schluter, ANALISI STATISTICA DEI DATI BIOLOGICI, Zanichelli editore S.p.A. Copyright © 2010
16 | 11
La stima può
dipendere
dall’intervallo di valori
considerato
M.C. Whitlock, Dolph Schluter, ANALISI STATISTICA DEI DATI BIOLOGICI, Zanichelli editore S.p.A. Copyright © 2010
16 | 12
I vari coefficienti di
correlazione
nell’esempio
r (Pearson) = 0.308
int.conf.95%: (0.02,0.55)
Test ρ = 0: P = 0.037
r (Kendall) = 0.234
Test ρ = 0: P = 0.033
r (Spearman) = 0.301
Test ρ = 0: P = 0.042
M.C. Whitlock, Dolph Schluter, ANALISI STATISTICA DEI DATI BIOLOGICI, Zanichelli editore S.p.A. Copyright © 2010
16 | 13
Si può calcolare il coefficiente di Spearman anche con dati
(non numerici) ordinali , ossia che si possono ordinare.
M.C. Whitlock, Dolph Schluter, ANALISI STATISTICA DEI DATI BIOLOGICI, Zanichelli editore S.p.A. Copyright © 2010
16 | 14