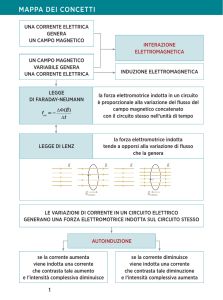
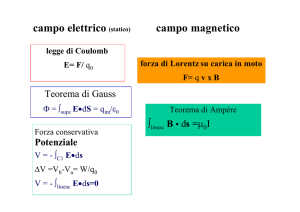
2. L’induzione elettromagnetica
Nel 1821 il fisico danese Oersted aveva osservato come la corrente stazionaria in un
filo generava un campo magnetico stazionario tutt’intorno. La parola stazionario indica
che il vettore B , pur non avendo intensità e direzione costanti, fissato un punto dello
spazio, il suo valore in quel punto non cambia nel tempo. Ad esempio, è stazionario il
campo espresso dalla legge di Biot e Savart, che ha direzione e verso che variano nello
spazio, ma non nel tempo. Negli anni immediatamente dopo il 1821 i fisici ritennero
ragionevole supporre che, così come la corrente generava un campo B , il campo B
stazionario avrebbe dovuto generare corrente. Questa ipotesi, per quanto verosimile, era
errata, perché un campo B stazionario, come sappiamo, non compie lavoro sulle
cariche, e non può quindi conferire loro l’energia che occorre per innescarne il
movimento in un circuito. Nel 1831 il fisico inglese Michael Faraday scoprì che, affinché
B potesse mettere in moto le cariche in un circuito, doveva attingere ad una sorgente
esterna di energia, che facesse variare l’intensità oppure la direzione e il verso di B . Il
campo magnetico variabile così prodotto, trasferiva l’energia dalla sorgente esterna alle
cariche, riuscendo a metterle in movimento. In questo modo Faraday stabilì l’esistenza
di una stretta connessione fra le variazioni del campo magnetico e l’apparire di un campo
elettrico, un fenomeno fisico fondamentale detto induzione elettromagnetica. In particolare
egli scoprì che le variazioni del flusso magnetico concatenato ad un circuito, generano
corrente nel circuito stesso.
B1
Induzione elettromagnetica
Quando il flusso magnetico concatenato ad un circuito chiuso subisce una variazione,
appare una corrente elettrica nel circuito stesso, detta corrente indotta.
B2
I
Consideriamo la figura a lato come esempio. Abbiamo una spira quadrata di filo
metallico, attraversata dalle linee di un campo magnetico uniforme B1 . Se facciamo
crescere il flusso del campo magnetico concatenato alla spira, aumentando il campo fino
a B2 , nella spira si genera la corrente indotta I , con il verso come nel disegno.
Che cosa indica l’apparire di questa corrente?
B A
f VB VA
L’apparire di una corrente indica che la variazione del flusso magnetico concatenato
produce nel circuito una forza elettromotrice f , detta forza elettromotrice indotta. Come
sappiamo, “forza elettromotrice” è il nome che si usa per indicare il lavoro per unità di
carica eseguito - in un percorso chiuso - dalle forze che producono la corrente. Se il circuito viene
aperto, come in figura, il valore di f si manifesta come differenza di potenziale
misurabile fra i capi A e B, dove si accumulano le cariche messe in moto nel circuito,
impossibilitate a completare il percorso chiuso. Analogamente, la forza elettromotrice di
una batteria è uguale alla differenza di potenziale che si misura fra i terminali della
batteria. Trattando i circuiti elettrici abbiamo visto che il campo elettrostatico, cioè quello
regolato dalla legge di Coulomb, è conservativo, cioè incapace di compiere lavoro su di
un percorso chiuso. Pertanto, ogni volta che c’è corrente in un circuito, e quindi una forza
elettromotrice, si produce nel circuito un particolare tipo di campo elettrico non
conservativo, capace di innescare il moto delle cariche in un percorso chiuso. Questo
campo originato dall’induzione elettromagnetica si dice campo elettrico indotto. Quindi, il
campo magnetico e il campo elettrico appaiono connessi, giacché una variazione del
flusso di B genera la comparsa di E indotto.
Quali leggi regolano il fenomeno dell’induzione elettromagnetica?
Gli esperimenti mostrano che la forza elettromotrice generata dall’induzione
elettromagnetica in un circuito, non dipende dal modo in cui il cambiamento nel flusso
4
magnetico viene prodotto, ma soltanto dalla rapidità con cui il flusso varia. Come sappiamo,
il flusso magnetico concatenato a un circuito dipende da tre grandezze fisiche: l’intensità
del campo, l’area delimitata dal circuito e l’angolo che il versore normale forma col
campo. Quindi possiamo produrre una forza elettromotrice in un circuito in tre modi:
(1) cambiando l’intensità del campo B concatenato al circuito (ad esempio mentre gli
avviciniamo o allontaniamo un magnete);
(2) variando l’area del circuito attraversata da B (ad esempio schiacciando una spira
circolare facendole assumere una forma ovale molto stretta);
(3) ruotando il circuito in modo che cambi la sua inclinazione rispetto al campo.
La forza elettromotrice indotta in tutti questi casi è sempre regolata dalla seguente:
Legge di Faraday-Neumann
La forza elettromotrice media indotta in un circuito in un intervallo t , è pari al rapporto
fra la variazione (B ) del flusso magnetico concatenato al circuito, e l’intervallo stesso,
cambiata di segno:
(B )
f
t
Quando l’intervallo t è così piccolo da chiudersi attorno ad un singolo istante, la forza
elettromotrice indotta istantanea è la variazione istantanea del flusso magnetico
concatenato - cioè la derivata rispetto al tempo di (B ) - cambiata di segno:
d (B )
f
dt
La Controfisica
In realtà Faraday, pur essendo il
primo ad aver dato notizia di aver
rivelato l’effetto, vista la sua avversione per la matematica, non
scrisse mai la formula che lega la
forza elettromotrice indotta alla
variazione del flusso concatenato.
Altri importanti esperimenti che
condussero alla formulazione
della legge dell’induzione, condotti quasi in contemporanea a
quelli di Faraday, si devono al
fisico statunitense Joseph Henry
(1797-1878). La legge dell’induzione elettromagnetica venne
stabilita matematicamente nel
1845 dal fisico tedesco Franz
Ernst Neumann (1798–1895), e
per questo è nota come legge di
Faraday-Neumann.
Come si esprime la fem in una spira che ruota in un campo uniforme?
Consideriamo una spira di area A che ruota con velocità angolare costante,
mantenendo il suo asse di rotazione (tratteggiato in figura) perpendicolare a un
campo magnetico uniforme B . Il versore n̂ normale alla spira forma con B un
angolo che in ogni istante si può scrivere t (proprio come nel moto rettilineo
uniforme si scrive x vt ). Quindi il flusso concatenato al circuito all’istante t è:
(t ) |B | A cos t
La derivata rispetto al tempo della funzione composta cos t è sin t , e quindi la
forza elettromotrice istantanea in funzione del tempo f (t ) risulta:
n̂
wt
B
f(t )
A |B |
f (t ) (t ) |B | A( sin t ) |B | A sin t
Che come si vede è una funzione oscillante, il cui valore massimo |B | A è tanto mag-
giore quanto maggiore è , cioè quanto più rapidamente avviene la rotazione, (e quindi
quanto più rapida è la variazione del flusso).
t
A |B |
Come si esprime la fem di un circuito che varia l’area attraversata dal campo B?
In un piano orizzontale, consideriamo un circuito di filo metallico, a forma di qua
drato, di lato , che sta uscendo a velocità v da una regione in cui c’è un campo
magnetico uniforme, B , avente direzione verticale. Inizialmente quadrato è interamente immerso nel campo, ma dall’istante in cui inizia ad uscire dalla regione, solamente una porzione della sua area è attraversata dalle linee del campo e contribuisce
al flusso magnetico concatenato. La porzione di quadrato HKMN è la sola in cui il
circuito ha flusso non nullo, ed essa diminuisce la sua area man mano che il circuito
si porta fuori dal campo. La sua area è A(t ) MK HK . Indicando con x (t ) la lunghezza della porzione di quadrato già fuori dalla zona del campo al tempo t , il flusso magnetico concatenato al circuito vale:
5
B
N
H
M
K
x (t )
v
(t ) |B | A(t ) cos 0 |B | MK HK |B | [ x (t )] |B | 2 |B | x (t )
Calcolando la derivata rispetto al tempo, la quantità costante |B | 2 scompare, e
ricordando che x (t ) v(t ) , la forza elettromotrice istantanea in funzione del tempo
f (t ) risulta:
f (t ) (t ) |B | v(t )
Se la velocità è costante, il di f (t ) si mantiene costante nel tempo finché il quadrato
non è completamente uscito dal campo magnetico.
La forza elettromotrice indotta dipende dal valore del flusso magnetico?
È importante notare che la forza elettromotrice indotta non dipende dal valore del flusso
magnetico concatenato, ma è legata alla rapidità del cambiamento di tale flusso. Infatti,
rapporto (B )/t è tanto più grande quanto più piccolo è l’intervallo in cui è
avvenuta la variazione. Sottolineiamo che questo rapporto fornisce solo un valore
medio della forza elettromotrice indotta durante t . La formulazione rigorosa della
legge di Faraday è quella tramite la derivata rispetto al tempo, che dà il valore di f
istante per istante.
Qual è il significato del segno meno nella legge di Faraday?
n̂
La Controfisica
Se per legare il versore normale
all’orientamento del percorso,
avessimo scelto la convenzione
della mano sinistra - anziché quella della mano destra - nella legge
di Faraday-Neumann ci sarebbe
stato un segno positivo.
B2
I
B
Ricordiamo che si ha un flusso concatenato di segno positivo quando le linee del campo
B attraversano la superficie delimitata dal circuito nel senso indicato dal versore n̂ . E se
il numero di linee di campo nel verso di n̂ aumenta, si ha d /dt 0 . Invece, la forza
elettromotrice f è positiva se produce corrente nel senso scelto come positivo per il
circuito. Come abbiamo visto però, il verso di n̂ e l’orientamento del circuito non sono
indipendenti, ma per convenzione si è stabilito che il versore normale deve sempre
puntare ad un osservatore che vede antiorario l’orientamento del circuito. Oppure – che è
lo stesso – i due versi sono legati dalla regola della mano destra. Avendo presente questa
scelta degli orientamenti, il segno meno davanti alla variazione del flusso indica che le
quantità f e d /dt hanno sempre segni opposti. Se aumenta il flusso in direzione di n̂ ,
la corrente indotta ha verso opposto all’orientamento del circuito, e se diminuisce il
flusso in direzione di n̂ , la corrente indotta ha il verso dell’orientamento del circuito. Ciò
significa che la corrente indotta è sempre diretta in modo da contrastare la variazione di
flusso che l’ha generata. Infatti, essa produce un proprio campo magnetico, il cui verso è
stabilito dalla regola della mano destra (come normalmente accade per tutti i campi
prodotti da una spira). In base alla scelta degli orientamenti, il flusso di questo campo
aggiuntivo ha lo stesso segno della corrente indotta. Esso, quindi, tende a riportare il
flusso concatenato al valore che aveva prima che la corrente comparisse. In figura è
riportata la sua direzione, con riferimento all’esempio di inizio paragrafo. Tale proprietà
è un corollario della legge di Faraday-Neumann, ma per la sua importanza viene
enunciata esplicitamente dalla seguente legge di Lenz.
Legge di Lenz
La corrente indotta genera a sua volta un campo magnetico, con verso tale da contrastare
la variazione del flusso magnetico che l’ha generata.
Che cosa prevede la legge di Lenz quando un magnete si avvicina ad una spira?
Come sappiamo, quanto più siamo vicini ad un magnete, tanto maggiore è l’intensità del
campo B . E tanto maggiore è anche il numero di linee di campo che attraversano l’unità
di superficie ortogonale, in accordo col criterio di Faraday. Quindi, in un moto relativo di
avvicinamento fra il magnete e una spira di filo conduttore, aumenta il flusso magnetico
concatenato alla spira stessa. Per effetto della legge dell’induzione di Faraday, nella spira
compare una corrente indotta, con verso tale da generare un campo magnetico le cui
6
linee tendono a riportare il flusso al valore precedente l’avvicinamento. Un modo
diverso di vedere il fenomeno è pensare che la spira in cui scorre la corrente indotta
diviene un elettromagnete i cui poli sono orientati in modo da respingere quelli del
magnete mentre avanza, esercitando su di esso una forza repulsiva. In figura il magnete
in avvicinamento ha il polo nord verso la destra di chi legge, quindi la corrente indotta
trasforma la spira. in un elettromagnete col nord a sinistra. Il fenomeno non dipende dal
fatto che sia la spira a spostarsi verso il magnete, oppure che sia il magnete a spostarsi
verso la spira, ma solo dall’esistenza di un moto relativo di avvicinamento. Viceversa, in
un moto relativo di allontanamento fra magnete e spira, il flusso concatenato diminuisce, e
fra i due oggetti si genera una forza attrattiva. Con riferimento alla figura, questa volta la
corrente indotta trasforma la spira in un magnete col sud alla sinistra di chi legge.
v
S
N
F
avvicinamento
In cosa si trasforma l’energia cinetica del magnete che viene rallentato?
La forza repulsiva che la legge di Lenz innesca fra la spira e il magnete che ad essa si
avvicina, esegue un lavoro resistente che rallenta il magnete. Mentre il magnete perde
velocità, la sua energia cinetica è convertita in energia cinetica degli elettroni che si
mettono in moto all’interno della spira, formando la corrente indotta. La corrente indotta
a sua volta produce un riscaldamento del circuito per effetto Joule, così che alla fine del
processo, l’energia cinetica del magnete sulla scala degli oggetti si è trasformata in energia
di agitazione termica sulla scala delle particelle. Sulla base di queste considerazioni,
appare chiaro che le forze attivate dalla legge di Lenz non potrebbero mai far aumentare la
velocità del magnete, perché altrimenti violerebbero la legge di conservazione dell’energia.
Infatti, il contenuto energetico del sistema isolato costituito dal magnete e dalla spira, non
può cambiare. Ad ogni diminuzione nell’energia cinetica in una parte di un sistema
isolato, deve necessariamente accompagnarsi un incremento energetico in un'altra sua
parte. Se, in assenza di azioni dall’esterno del sistema spira-magnete, il magnete
aumentasse la propria velocità, e contemporaneamente il filo si riscaldasse per effetto
Joule, avremmo incrementato l’energia complessiva del sistema senza attingere ad alcuna
sorgente, violando i principi della fisica. Analogamente, anche il magnete in
allontanamento dalla spira viene rallentato dal lavoro resistente delle forze innescate dal
fenomeno dell’induzione magnetica, e la sua energia cinetica convertita in energia di
agitazione termica al livello delle particelle. Per mantenere il magnete in moto a velocità
costante, in allontanamento o avvicinamento, è necessario che una forza esterna al
sistema compia lavoro sul magnete, in modo da mantenerne costante l’energia cinetica.
Il lavoro di una forza esterna è necessario in tutti i casi d’induzione esaminati?
Sì, in presenza di un campo magnetico uniforme, bisogna lavorare dall’esterno sia per far
ruotare una spira con velocità angolare costante, sia per mantenere in moto la barretta
mobile del circuito con le due rotaie collegate. In mancanza di lavoro esterno, la spira
rotante e la barretta mobile si arresterebbero non appena tutta la loro energia cinetica
iniziale fosse stata trasformata in energia di agitazione termica delle particelle cariche in
moto. Uno dei modi in cui le centrali idroelettriche producono corrente è proprio quello
di far lavorare la forza gravitazionale, facendo mantenere in rotazione una spira in un
campo magnetico attraverso il flusso di acqua che, precipitando da una cascata colpisce
delle pale solidali alla spira, simili a quelle di una ruota di mulino.
Una legge di Lenz “al contrario”, produrrebbe una sorgente inesauribile di energia?
Supponiamo che il verso della corrente indotta fosse opposto a quello stabilito dalla legge
di Lenz. L’avvicinamento di un magnete ad una spira produrrebbe allora un ulteriore
aumento di flusso magnetico dovuto al campo magnetico generatosi nella spira stessa.
Tale campo, infatti, anziché contrastare l’incremento di flusso dovuto al movimento del
magnete, contribuirebbe alla sua crescita. Con il risultato che la corrente indotta
aumenterebbe ancora di più a causa del flusso aggiuntivo da essa stessa generato, e il
fenomeno si sosterrebbe da solo, senza bisogno di compiere lavoro dall’esterno.
7
I
v
S
N
F
allontanamento
I
Avremmo un dispositivo che, violando le leggi della fisica, genererebbe corrente – e
quindi energia – senza attingere ad una sorgente esterna.
Che cosa s’intende per forza elettromotrice cinetica e come si calcola?
FL
E
v
B
Consideriamo un conduttore rettilineo, ad esempio una barretta metallica, che avanza con
velocità v , perpendicolarmente alle linee di un campo magnetico B . Gli elettroni di
conduzione, liberi di muoversi nel metallo, per effetto della forza di Lorentz si
accumulano ad un estremo e svuotano l’altro: Si produce così una separazione di carica,
che può fungere da forza elettromotrice se la barretta costituisce la parte mobile di un
circuito più grande. Per calcolare il valore di questa fem cinetica si può applicare la legge
di Faraday-Neumann, in modo opportuno collegando la barra ad un circuito e calcolando
la variazione di flusso magnetico. Tuttavia riesce più semplice concentrarsi solo sulla
barretta mobile, e calcolare il valore della fem cinetica attraverso la forza di Lorentz,
seguendo un ragionamento che si basa sul raggiungimento di una situazione di
equilibrio nella barretta. Le cariche nella barretta subiscono una forza qvB per effetto
della quale si mettono in moto all’interno del conduttore, cioè perpendicolarmente al
campo magnetico. Gli elettroni, non potendo lasciare il conduttore, si accumuleranno ad
uno dei due capi, lasciando nell’altro un eccesso di carica positiva. La separazione di
carica così prodotta, genera nella barretta un campo elettrico, che contrasta l’accumulo di
carica negli estremi, fino ad arrestarlo del tutto quando si crea la condizione di equilibrio:
q |E | q |v ||B |
La forza elettromotrice ai capi di una barretta di lunghezza è il lavoro per unità di
carica delle forze elettriche. Il suo modulo è dunque:
|fem| |E | |B | |v |
Ricordiamo ora che |B | esprime le linee di campo per metro quadro di area ortogonale al
campo, e osserviamo che |v | x /t A/t è proprio l’area spazzata ogni
secondo nel piano dove si muove il conduttore, che in questo caso è ortogonale a B .
Come possiamo generalizzare la formula se v,B ed non sono ortogonali fra loro?
B
n̂
v
v
In generale, il conduttore si può muovere su di un piano il cui versore n̂ forma un
angolo qualsiasi con il campo. Inoltre, la velocità può non essere perpendicolare al
conduttore stesso, se rettilineo. La formula della fem cinetica va modificata osservando
che nel caso della barretta, la formula si può leggere:
componente di componente di
distanza fra gli
|fem|
B piano del moto v conduttore estremi del conduttore
v
Quindi nel caso generale, |B | viene sostituito dalla quantità |B | |B | cos , che è la
componente di B lungo n̂ , e rappresenta le linee per metro quadro di superficie del
piano dove si muove il conduttore. Il fattore |v | va rimpiazzato con la quantità |v | ,
componente della velocità perpendicolare al conduttore. Allora, si vede bene come la
quantità |v ||B| rappresenti il numero di linee tagliate dal conduttore ogni secondo:
area spazzata nel
x
A
| fem | |v| |B |
|B|
|B| piano del moto
t
t
ogni secondo
numero linee al m 2
piano del moto
Se poi il moto è più complicato di un semplice moto piano di traslazione, occorrono gli
strumenti del calcolo integrale per calcolare la fem. Vale però la proprietà generale:
8
La forza elettromotrice indotta ai capi di un conduttore in moto è data dal numero di
linee di campo magnetico che il conduttore taglia ogni secondo.
La formula | fem | |B | |v | della forza elettromotrice cinetica vale anche se la velocità
o la lunghezza del conduttore rettilineo cambiano nel tempo. Essa fornisce solo il modulo
della forza elettromotrice, per avere il segno bisogna applicare la legge di Lenz o
ragionare sull’accumulo di carica prodotto dalla forza di Lorentz.
In che modo possiamo ottenere questo risultato tramite la legge di Faraday-Neumann?
Consideriamo un circuito come quello in figura, formato da due rotaie collegate, e
dalla una barra conduttrice mobile che scorre verso destra a velocità costante v . Il
B
dispositivo è immerso in un campo magnetico B , perpendicolare al piano del cirI
cuito. Indichiamo con la lunghezza del tratto che unisce le rotaie, e con x (t ) la di
x (t )
stanza della barra mobile da questo tratto. Scegliamo come versore normale quello
che punta al lettore e, di conseguenza, verso di percorrenza positivo del circuito
quello che il lettore vede antiorario. Il flusso magnetico concatenato vale:
(t ) |B | x (t )
v
La fem istantanea f (t ) è la derivata rispetto al tempo del flusso, cambiata di segno.
Come sappiamo dalla cinematica, x (t ) v(t ) quindi:
f (t ) (t ) |B | v(t )
Il segno meno nella forza elettromotrice indica che la corrente indotta scorre in senso
opposto al verso di percorrenza positivo del circuito. Va osservato che, se si desidera
mantenere a velocità costante la barra, occorre l’azione di una forza esterna verso destra,
altrimenti la barra rallenta per l’azione della forza magnetica verso sinistra, che il campo
B esercita sulla barra non appena inizia a scorrere la corrente indotta.
Quanto spazio percorre la barretta prima di arrestarsi se non agisce la forza esterna?
Se la forza esterna non è presente, la velocità della barretta diminuisce nel tempo.
Applichiamo la formula della fem cinetica con un valore di velocità variabile v(t ) , nel
caso in cui campo, velocità e barretta sono ortogonali fra loro:
|fem| |B | v (t )
Possiamo calcolare lo spazio percorso prima di arrestarsi osservando che, se R è la
resistenza complessiva del circuito, la forza magnetica ha intensità:
fem
|B | 2 2v(t )
|FM | |IL B | |I ||B |
|B |
R
R
La forza magnetica agisce verso sinistra. Lungo un asse delle ascisse orientato verso
destra possiamo scrivere la seconda legge della dinamica per la barretta, indicandone con
m la massa:
|B | 2 2v
F
ma
R
Scrivendo a v /t e v x /t , e semplificando t si ottiene la relazione:
|B | 2 2
x m v
R
Lo spazio x necessario per far arrestare la barretta si calcola imponendo che il
cambiamento di velocità v sia quello dal valore iniziale v finché non si ferma, cioè
v 0 v . Sostituendo si ottiene:
9
B
FM
I
x
x
mvR
|B | 2 2
Che succede alla velocità se invece continua ad agire una forza esterna costante?
Supponiamo la barra inizialmente ferma. Per l’azione della Fest il conduttore si mette in
moto con una velocità che in una prima fase non è costante, ma il cui valore v(t )
aumenta col tempo. Avendo già visto che |FM | |B | 2 2v(t )/R , la legge di Newton si
scrive:
Fest
|B | 2 2v(t )
ma
R
Ragionando sull’equazione ottenuta si vede la velocità v , inizialmente nulla, aumenta in
modo uniforme a causa di Fest , ma l’aumento è contrastato dalla forza magnetica, tanto
maggiore quanto più grande è v(t ) . Non appena la velocità raggiunge quel valore per cui
forza magnetica e forza di gravità sono uguali, l’accelerazione si annulla. Da quel
momento in poi la velocità resterà costante. Indichiamo con vL , questo valore costante,
che viene detto velocità limite , e che si ricava imponendo a 0 :
vL
RFest
|B | 2 2
Come si calcola la fem cinetica se il conduttore è di forma irregolare?
H
B
K
Se il conduttore non è rettilineo, ma ha una forma irregolare, e si muove di sola
traslazione, la forza elettromotrice cinetica che genera è uguale a quella prodotta da un
conduttore rettilineo che unisce gli estremi di quello irregolare, perché i due tagliano lo
stesso numero di linee ogni secondo. Infatti, il conduttore chiuso che si viene così a
creare, non subisce alcuna variazione di flusso magnetico concatenato Quindi la forza
v
elettromotrice ai capi del conduttore rettilineo che unisce gli estremi ha uguale valore (e
senso opposto) rispetto a quella ai capi del conduttore irregolare. Ad esempio, per
calcolare la fem cinetica ai capi H e K del filo metallico ricurvo in figura, non è necessario
conoscere il dettaglio di ciò che accade in tutte le sue parti. Se conosciamo la velocità v
alla quale esso spazza l’area, possiamo applicare la formula |fem| |v ||B| con
HK , distanza fra gli estremi.
I
O
Come si calcola la fem fra due contatti che strisciano contro un conduttore in moto?
C
V
A
B
B
V
Consideriamo ora un conduttore esteso, detto disco di Faraday. Si tratta di un disco
metallico che ruota con velocità angolare costante , immerso in un campo magnetico
uniforme B perpendicolare al piano del disco stesso. Ci proponiamo di calcolare la fem
che si produce fra due contatti striscianti fissi nello spazio, mentre il conduttore,
scorrendo si strofina contro di essi. Che s’instauri una fem fra il contatto strisciante A,
posto sul bordo del disco, e il contatto strisciante O, posto sull’asse centrale attorno a cui il
disco ruota, si deduce osservando che gli elettroni, liberi di muoversi, sono spinti verso il
bordo esterno perché, ruotando subiscono l’azione della forza di Lorentz FL qv B ,
in direzione radiale. Con riferimento alla nostra figura, il punto O, è continuamente
A
svuotato di elettroni, e quindi mantenuto a potenziale maggiore del punto A.
C
Cambiando il senso di rotazione oppure verso del campo, la forza di Lorentz punta
invece verso il centro. Anche effetti centrifughi contribuiscono, in misura molto minore,
O
allo spostamento di elettroni in direzione radiale. Come abbiamo visto, la forza
elettromotrice indotta fra due punti è data dal numero di linee di campo tagliate ogni
secondo dal segmento che sul conduttore unisce i due punti. Si traccia allora segmento
10
che unisce i contatti striscianti e si calcola il numero di linee di campo che ogni secondo
questo segmento attraversa, mentre si sposta insieme al conduttore. Il percorso della
corrente all’interno del disco non è noto, tuttavia, considerato il verso della rotazione, si
può supporre un tragitto geometricamente semplice, come il tratto AC lungo il bordo,
seguito dal raggio CO. Si individua così il circuito A-C-O-V-A, attraverso il quale
calcolare la variazione del flusso magnetico concatenato, dove V indica un voltmetro che
misura la differenza di potenziale fra i contatti striscianti. Poiché B rimane costante e il
dispositivo è sempre fermo, il solo di cambiamento di flusso proviene dall’incremento di
area da esso delimitata. Come abbiamo visto, il cambiamento di flusso può essere anche
scritto come numero di linee di campo tagliate, ogni secondo, dalla parte mobile del
circuito, cioè dal raggio OC. In un intervallo di tempo t , il raggio OC ruota di un
B
FL
e
v
angolo , spazzando il settore circolare AOC di area A 1 r 2 . L’area A è
2
attraversata ortogonalmente da un numero di linee di campo che si scrive |B | A ,
infatti, |B | esprime il numero di linee per unità di superficie ortogonale ad esse. La forza
elettromotrice fra A e O è quindi:
|B | 12 r 2 1 2
linee tagliate in t
|B | A
fem
|B | r
t
t
t
2
dove abbiamo usato la relazione /t . Osserviamo ora che qualunque altro
percorso la corrente segua all’interno del disco per andare da A ad O, esso taglia un
uguale numero di linee di campo nell’unità di tempo. Infatti, una curva nel disco può
essere scomposta in tanti piccoli tratti radiali e tratti circolari consecutivi. Poiché i tratti
circolari non tagliano alcuna linea di campo durante la rotazione, mentre la somma dei
tratti radiali riproduce il raggio r del disco, spezzettato, il risultato che si ottiene per la
fem è lo stesso, qualunque sia il percorso della corrente.
Esercizi
18. Un avvolgimento di N 300 spire circolari di raggio r 3.60 cm , di resistenza
R 6.00 giace su un piano orizzontale, immerso in un campo magnetico uniforme
verticale, diretto dal basso in alto, d’intensità |B | 0.500 T . Si calcoli la corrente indotta
media nell’avvolgimento se: (a) la spira viene ruotata di 180° in t 0.150 s ; (b) in un
intervallo t 0.150 s le spire vengono schiacciate al punto che l’area racchiusa diviene
nulla. (c) Calcolare la corrente indotta istantaneamente se le spire ruotano attorno al loro
asse orizzontale passante per il centro, con una velocità angolare costante 4.00 rad/s
.
(a) Calcoliamo il flusso magnetico concatenato inizialmente all’avvolgimento, quando il
versore normale è parallelo al campo magnetico:
1 (B ) N |B | A cos 0 N |B | r 2
B
n̂
Dopo che la spira è stata ruotata di 180 il flusso è diventato:
2 (B ) N |B | A cos 180 N |B | r 2
La forza elettromotrice media generata dal capovolgimento di 180° è:
1
(N |B | r 2 N |B | r 2 ) 2N |B | r 2
fa
2
t
t
t
t
2 300 0.500 3.14 0.03602
8.14 V
0.150
e la corrente indotta media vale:
f
8.14
Ia a
A 1.36 A
R
6.00
(b) La forza elettromotrice media, si calcola osservando che dopo lo schiacciamento
2 (B ) 0 :
11
n̂
wt
B
2 1
(0 N |B | r 2 ) N |B | r 2
fb
t
t
t
t
300 0.500 3.14 0.03602
4.07 V
0.150
e la corrente indotta media vale:
f
4.07
Ib b
A 0.678 A
R
6.00
(c) Mentre la spira ruota, il suo versore n̂ forma con il campo B un angolo che
all’istante t vale t . Quindi il flusso concatenato al circuito all’istante t è:
(t ) N |B | A cos t
Calcolando la derivata di questa espressione abbiamo la forza elettromotrice
istantanea in funzione del tempo:
f (t ) (t ) N |B | A( sin t ) N |B | A sin t
4.00 300 0.500 3.14 0.03602 sin 4.00t 2.44 sin 4.00t
Che come si vede è una funzione oscillante, il cui valore massimo N |B | A 2.44 V è
tanto maggiore quanto maggiore è , cioè quanto più rapidamente avviene la rotazione,
(e quindi la variazione del flusso). La corrente indotta all’istante t vale:
f (t) 2.44 sin 4.00t
i(t )
0.407 sin 4.00t
R
6.00
R
B
x (t )
19. Una barra metallica di massa m 400 g scivola senz’attrito lungo un binario
verticale. Le rotaie sono separate da una distanza 90.0 cm , hanno resistenza
trascurabile come la barretta, e sono collegate da un resistore R 0.500 . Il dispositivo
è immerso in un campo magnetico uniforme, orizzontale, perpendicolare al piano del
circuito, d’intensità |B | 0.600 T . Mostrare che l’accelerazione della barretta diviene
nulla dopo una fase iniziale, e calcolare la velocità costante alla quale essa scende.
v(t)
R
I
FM
mg
Nel circuito composto dai binari, dalla resistenza, e chiuso dalla barretta, deve scorrere
corrente indotta I come in figura. Infatti, in questo modo l’aumento del flusso causato
dallo scendere della barretta tende ad essere compensato dal campo magnetico generato
dalla corrente indotta, che è entrante nel foglio e quindi di verso opposto a B .
Scegliendo come versore normale quello uscente dal foglio, il verso di percorrenza
positivo del circuito appare antiorario al lettore, e quindi ci aspettiamo che I abbia segno
negativo. La velocità di caduta v(t ) non è costante, perché la barretta parte da ferma e
accelera sotto l’azione della gravità, ed è frenata dalla forza magnetica. Indicando con
x (t ) la distanza della barretta dalla resistenza R , risulta per il flusso concatenato:
|B | x (t )cos 0 |B | x (t )
Osservando che la sola quantità variabile nel flusso è x (t ) , la cui derivata vale:
x (t ) v(t )
Abbiamo per la forza elettromotrice indotta e per la corrente:
|B | v(t )
d
fem
fem [ |B | x (t )] |B | x (t ) |B | v(t ) I
dt
R
R
Il segno meno indica scorrimento contro il verso positivo del circuito, come ci
aspettavamo. Come si vede, il risultato è lo stesso che si ottiene con la formula per la forza
elettromotrice cinetica: | fem | |B | |v | |B | |v (t )| . Per calcolare il modulo della
forza magnetica inseriamo il modulo della corrente nella formula:
|B | v(t )
|B | 2 2v(t )
| FM | |I || L || B | sin 90
( | B | 1)
R
R
12
La FM è diretta verso l’alto, a contrastare la forza peso, che esegue il lavoro necessario a
far scendere la barretta. Dalla seconda legge della dinamica abbiamo:
|B | 2 2v(t )
| FM | mg ma
mg ma
R
Ponendo che la barretta sia lasciata andare da ferma, man mano che cresce la velocità di
caduta v(t ) , aumenta anche la corrente, e con essa aumenta | FM | . Al contrario, la forza
peso rimane costante. L’accelerazione prodotta dalla differenza fra queste due forze,
diminuisce col tempo, finché non diviene nulla quando la forza magnetica uguaglia, in
intensità, la forza peso. Da quel momento in poi la velocità non aumenta più ma si
mantiene ad un valore costante vL , che si trova imponendo a 0 :
|B |2 2vL
Rmg
0.500 0.400 9.81
mg 0 vL
m/s 6.73 m/s
2
2
R
|B |
0.6002 0.9002
20. Sopra a un piano orizzontale, un filo di rame scorre senz’attrito, a velocità costante
v 0.200 m/s , a contatto con altri due fili saldati per il capo A . Si crea così un circuito a
forma di triangolo equilatero come in figura, il cui lato (t ) aumenta nel tempo, ed è
immerso in un campo magnetico verticale uniforme, d’intensità |B | 0.280 T . Sapendo
B
A
v
che la resistività del rame è 1.69 108 m , e che la sezione dei fili ha raggio
r 0.600 mm , esprimere in funzione del tempo, la forza elettromotrice indotta nel
circuito dal campo B . Calcolare la corrente nel circuito.
L’altezza h(t ) del triangolo equilatero è pari alla distanza percorsa dal filo che avanza a
velocità v , partendo dal vertice A dove sono saldati gli altri due fili:
h(t ) vt
e quindi la misura del lato del triangolo in funzione del tempo vale:
h(t )
3
(t )
2
(t )
2
h(t )
2
vt
3
3
Scegliamo la normale orientata verso il lettore, e quindi verso positivo quello che al lettore
appare antiorario. La forza elettromotrice e la corrente indotta valgono:
1
1
|B | v 2 2
2
(t ) |B | A cos 0 |B | h(t ) (t ) 1 |B | vt
vt
t
2
2
3
3
Indicando con R la resistenza del triangolo:
|B | v 2
2 |B | v 2
fem
fem (t ) 2
t I
t
R
3
3R
In alternativa possiamo ritrovare questo risultato applicando la tecnica della forza
elettromotrice cinetica. La porzione di conduttore mobile compresa nel circuito è lunga
(t ) (2 / 3)vt , quindi ai suoi capi si stabilisce una forza elettromotrice:
2
fem |B | v (t )
|B | v 2t
3
Dalla seconda legge di Ohm possiamo calcolare R ed inserirla:
R
I
Ltriangolo
S filo
2 |B | v 2
3(t )
r
2
3
r
2
2
3
vt
2 |B | v 2 r 2 3
|B | v r 2
t
t
6vt
3
3
3R
Il segno meno indica che la corrente indotta scorre contro il verso positivo di percorrenza
del circuito, cioè in senso orario per il lettore. Calcoliamo la corrente, il cui valore è
costante nel tempo:
13
(t )
0.280 0.200 3.14 (0.600 103 )2
A 1.25 A
I
3 1.69 108
B
C
21. Una barretta metallica di massa m scivola senza attrito lungo un binario di resistenza
elettrica trascurabile (come quella della barretta), inclinato di un angolo . Le rotaie sono
separate fra loro da una distanza , e collegate elettricamente nel punto più alto da un
condensatore di capacità C . Il dispositivo è immerso in un campo magnetico uniforme
B , verticale, diretto in alto. Calcolare l’accelerazione con cui la barretta scende.
n̂
Per ottenere l’accelerazione occorre conoscere l’intensità di tutte le forze che compiono
lavoro sulla barretta. Oltre alla gravità, non appena si genera corrente indotta per effetto
dell’aumento del flusso concatenato al circuito causato dal moto della barra, agisce la
forza magnetica FM IL B in direzione perpendicolare a B e alla barretta, come in
figura. Proiettando lungo i binari queste due forze, dalla seconda legge della dinamica
otteniamo il valore dell’accelerazione:
| FM | cos mg sin ma
Dobbiamo quindi ricavare l’intensità di FM , per la quale ci occorre il valore della
B
n̂
FM
I
corrente. La corrente è la derivata della funzione Q(t ) , che a sua volta esprime la carica
mg
complessivamente passata attraverso una sezione della barretta, dall’istante iniziale fino
al tempo t , e depositata sull’armatura del condensatore. Come sappiamo dalla
definizione di capacità, la carica sul condensatore è legata in ogni istante alla differenza di
potenziale VC (t ) fra le sue armature dalla relazione:
Q(t ) C VC (t )
E quindi sostituendo nella definizione di corrente, e osservando che, nella derivata
rispetto al tempo, C è solo una costante moltiplicativa:
I Q (t ) CVC (t )
In base alla legge di Ohm, la differenza di potenziale fra le armature del condensatore è
uguale alla forza elettromotrice indotta dovuta al moto della barretta. Indicando con v(t )
la velocità – crescente - con cui scende la barretta, la forza elettromotrice cinetica vale:
| f | |B | v |B | cos v(t ) VC (t )
Ricordando ora che l’accelerazione è la derivata della velocità, v (t ) a abbiamo:
I CVC (t ) C |B | cos v (t ) C |B | cos a
Il verso della corrente deve apparire orario ad un osservatore in alto, in modo che il
campo magnetico da essa creato sia verso il basso, a compensare l’aumento del flusso
verso l’alto, come previsto dalla legge di Lenz. Per calcolare il modulo della forza
magnetica ci occorre solo il modulo della corrente:
| FM | |I || L || B | sin 90 (C |B | cos a )( | B | 1) C |B | 2 2a cos
Possiamo infine ricavare l’accelerazione sostituendo | FM | nell’equazione impostata
precedentemente a partire dalla seconda legge della dinamica:
a(C |B | 2 2 )cos2 mg sin ma
a
B (t )
r
mg sin
m C |B | 2 2 cos2
22. Una spira circolare di raggio r 60.0 cm è immersa in un campo magnetico
uniforme B0 0.0900 T , attraversata perpendicolarmente dalle linee di B come in
figura. Ad un certo istante l’intensità del campo inizia a variare nel tempo, secondo la
legge B(t ) B0 0.0400t 2 . Sapendo che la spira è costruita con un filo d’argento
14
( 1.62 108 m) di sezione S 1.20 mm2 , calcolare la corrente indotta al suo
[R: 2.26 A,oraria ]
interno dopo 4.00 s , e stabilirne il verso.
Scegliamo la normale orientata verso il lettore, e quindi verso positivo quello che al lettore
appare antiorario. La forza elettromotrice e la corrente indotta valgono:
(t ) |B(t )| A cos 0 (B0 0.0500t 2 )r 2
fem (t )
d
(B r 2 r 2 0.0400t 2 ) 2r 2 0.0400t r 2 0.0800t
dt 0
fem
r 2 0.0800t
R
R
La resistenza della circonferenza è:
L
2r
R
S
S
Per la corrente risulta:
I
fem
r 2 0.0800t
rS 0.0800t
R
2r
2
S
E dopo 4.00 s :
I
I (4.00 s)
0.600 1.20 106 0.0800 4.00
A 2.26 A
6.28 1.62 108
Il segno positivo indica uno scorrimento contro il verso di percorrenza, pertanto la
corrente appare oraria al lettore.
y
23. In un piano orizzontale, si ha un filo piegato a forma di parabola, di equazione
y kx 2 , su cui scorre senz’attrito una barra conduttrice. La barra parte ferma dall’origine
avanzando di moto uniformemente accelerato lungo l’asse delle ordinate, con velocità
v(t ) at . Esprimere la forza elettromotrice indotta nel circuito in funzione del tempo.
Suggerimento: in base al teorema di Archimede, l’area di un segmento parabolico è due
terzi dell’area del rettangolo HKLM in cui è inscritto.
[R: fem (|B | 2a 3 /k )t 2 ]
L’area del circuito che si viene a creare è un segmento parabolico inscritto in un
rettangolo di base 2x ed altezza y kx 2 . L’area di tale segmento, in funzione di x , si
scrive:
2
2
4
A(x ) 2x y 2x kx 2 kx 3
3
3
3
Per avere l’area in funzione del tempo osserviamo che nel moto rettilineo uniformemente
accelerato, se la barra parte ferma dell’origine e la sua accelerazione è ay a :
1
1
y y0 v0y t ay t 2 at 2
2
2
Considerato che tutte le quantità sono positive, risulta:
y
at 2
x
k
2k
3
4 at 2
4 a 3t 6 1 16k 2a 3t 6
1 2a 3 3
A(t ) k
t
k
3 2k
3 8k 3 3
3 k
8k 3
Scegliamo la normale orientata verso il lettore, e quindi verso positivo quello che al lettore
appare antiorario. La forza elettromotrice vale:
1 2a 3 3
(t ) |B | A(t ) cos 0 |B |
t
3 k
fem (t ) |B |
2a 3 2
t
k
15
H
v(t)
M
O
L x
B
K
v
L
B
h (t )
O
M
24. In un piano orizzontale, un filo di rame scorre senz’attrito, a velocità costante
v 0.300 m/s , a contatto con altri due fili perpendicolari fra loro, saldati per il capo O .
Si crea così un circuito a forma di triangolo rettangolo con angolo alla base costante
30 , e la cui altezza h(t ) aumenta nel tempo. Il circuito è immerso in un campo
magnetico verticale uniforme, d’intensità |B | 0.180 T . Sapendo che la resistività del
rame è 1.69 108 m , e che la sezione dei fili ha raggio r 0.800 mm , esprimere
in funzione del tempo, la corrente indotta nel circuito dal campo B . Calcolare la corrente
nel circuito.
[R: I 2.77 A (oraria per chi legge) ]
L’altezza h(t ) del triangolo rettangolo è pari alla distanza percorsa dal filo che avanza a
velocità v , partendo dal vertice O dove sono saldati gli altri due fili:
h(t ) vt
e quindi le misure dei cateti del triangolo in funzione del tempo valgono:
h(t )
vt
OM sin h(t ) OM
2vt
sin 30 1/2
h(t )
vt
2vt
sin 60
3 /2
3
L’area A(t ) del triangolo rettangolo in funzione del tempo è:
OL sin(90 ) h(t )
OL
1
1
2vt
2v 2 2
A(t ) OL OM sin 2vt
t
2
2
3
3
Scegliamo la normale orientata verso il lettore, e quindi verso positivo quello che al lettore
appare antiorario. La forza elettromotrice e la corrente indotta valgono:
2v 2 2
(t ) |B | A(t )cos 0 |B |
t
3
Indicando con R la resistenza del triangolo:
|B | v 2
4 |B | v 2
fem
fem (t ) 4
t I
t
R
3
3R
Dalla seconda legge di Ohm possiamo calcolare R ed inserirla:
2 2
Ltriangolo
OL OM LM
1 2
2
R
vt 2vt
vt (2vt )
2
2
3
S filo
r
r 3
1 2
4
vt 6 2 3
R
vt 2vt vt
2
2
r 3
r
3
3
4 |B | v 2
4 |B | v 2
r 2 3
4 |B | vr 2
I
t
t
3R
3
vt(6 3)
(6 3)
Il segno meno indica che la corrente indotta scorre contro il verso positivo di percorrenza
del circuito, cioè in senso orario per il lettore. Calcoliamo la corrente:
4 0.180 0.300 3.14 (0.800 103 )2
A 3.32 A
I
8
(6 3) 1.69 10
R
I
B
F
25. Una barretta metallica tirata da una forza costante F , scivola senz’attrito, alla velocità
di 3.00 m/s , lungo un binario orizzontale. Le rotaie sono separate da una distanza
70.0 cm , hanno resistenza trascurabile come la barretta, e sono collegate da un
resistore R 1.25 . Il dispositivo è immerso in un campo magnetico perpendicolare al
piano del circuito, d’intensità |B | 0.500 T . Nel circuito che si viene a formare, scorre
una corrente I 2.00 A come in figura. Calcolare l’intensità di F .
[R: 0.294 N ]
16
La forza elettromotrice cinetica e la corrente indotta valgono:
| fem |
|B | v
| fem | |B | v I
R
R
La corrente indotta scorre in senso orario, come in figura, perché il campo che essa crea
dev’essere entrante nella pagina, per compensare l’aumento di flusso in direzione
uscente causato dall’avanzare della barretta. Per calcolare il modulo della forza magnetica
inseriamo modulo della corrente nella formula:
|B | v
|B |2 2v
| FM | |I || L || B | sin 90
( | B | 1)
R
R
La forza magnetica è diretta verso sinistra, e dalla seconda legge della dinamica abbiamo
che per far avanzare la barretta a velocità costante (e quindi accelerazione nulla) occorre
una forza F verso destra, d’intensità e direzione uguali a quelle della forza magnetica.
Orientando un asse delle ascisse verso destra si ha:
Fx | FM | | F | max 0
| F | | FM |
|B | 2 2v
0.5002 0.7002 3.00
| F | | FM |
N 0.294 N
R
1.25
26. Una barretta metallica scivola senz’attrito, alla velocità di 2.50 m/s , lungo un binario
orizzontale. Le rotaie sono separate da una distanza 55.0 cm , hanno resistenza
trascurabile, e sono collegate da un resistore R1 1.00 ai capi di sinistra, e da
v R
2
R1 B
R2 3.00 ai capi di destra. Il dispositivo è immerso in un campo magnetico
perpendicolare al piano del circuito, d’intensità |B | 0.400 T . Calcolare la differenza di
potenziale ai capi della barretta e la corrente che vi scorre, sapendo che la sua resistenza
vale R 2.00 .
[R: 0.550 V, 2.00 A ]
Utilizzando la tecnica della forza elettromotrice cinetica, ai capi della barretta si stabilisce
una forza elettromotrice:
fem |B | v
Si giunge allo stesso risultato scegliendo una qualunque delle due maglie che si formano,
una per ogni resistenza, mentre scorre la barretta, e calcolando la forza elettromotrice
come derivata del flusso in una di esse. Il circuito pertanto equivale allo schema
rappresentato a lato. La resistenza equivalente si calcola considerando che R1 ed R2 sono
in parallelo, e la resistenza R12 ed esse equivalente è in serie ad R :
RE R R12 R
1.00 3.00
2.75
2.00
R1 R2
1.00 3.00
R1R2
R1
f |B |l v
R2
R
V fem |B | v (0.400 2.50 0.550) V 0.550 V
|B | v
fem
0.400 2.50 0.550
I
A 2.00 A
RE
RE
2.75
27. Una barretta metallica di resistenza trascurabile, scivola senz’attrito su un binario
orizzontale lungo 2 160 cm , seguendo un moto armonico di equazione
x (t ) sin t , con 2.40 rad/s ed equilibro nel punto centrale del binario. Le rotaie
sono separate da una distanza 80.0 cm , e sono dei fili di rame ( 1.69 108 m )
la cui sezione ha raggio r 1.50 mm . Il dispositivo è immerso in un campo magnetico
perpendicolare al piano del circuito, d’intensità |B | 0.0130 T . Calcolare la differenza
di potenziale ai capi della barretta e la corrente che vi scorre, in funzione del tempo.
62.6 cos 2.40t
A]
[R: f (t ) 2.00 102 cos 2.40t V, I (t )
5 4 cos2 2.40t
17
x(t )
B
x(t )
R1
f
R2
Utilizzando la tecnica della forza elettromotrice cinetica, ai capi della barretta si stabilisce
una forza elettromotrice:
f |B | v(t ) |B | x (t ) |B | 2 cos t 0.0130 0.800 0.800 2.40 cos 2.40t
f 2.00 102 cos 2.40t
Il circuito equivale allo schema qui a lato, dove le resistenze dei due tratti di binario
possono essere calcolate tramite la seconda legge di Ohm, e sono in parallelo fra loro:
2[ x (t )]
3 2 sin t
R1
2
r
r 2
2[ x (t )]
3 2 sin t
R2
2
r
r 2
Calcoliamo la resistenza equivalente:
R1R2
[3 2 sin t ] [3 2 sin t ]
RE
R1 R2
r 2 3 2 sin t 3 2 sin t
92 4 2 sin2 t
[5 4(1 sin2 t )]
(5 4 cos2 t )
2
2
2
6
r
6r
6r
Calcoliamo la corrente nella barretta:
f
6r 2 |B | 2 cos t
6r 2 |B |
cos t
I
2
RE
(5 4 cos t )
5 4 cos2 t
H
B
v
A
6 3.14 (1.50 103 )2 0.0130 0.800 2.40
8
cos 24.0t
2
1.69 10
5 4 cos 24.0t
62.6 cos 2.40t
5 4 cos2 2.40t
28. Una barretta metallica di resistenza R 2.25 , scivola senz’attrito
su di una
8
circonferenza di raggio r 120 cm fatta di filo d’alluminio ( 2.75 10 m ), la cui
sezione ha diametro d 0.600 mm . Il dispositivo è immerso in un campo magnetico
perpendicolare al piano del circuito, d’intensità |B | 0.250 T . Fissato un riferimento in
cui il centro della circonferenza è nell’origine, e la barretta, parallela alle ordinate, parte
dal punto A con velocità costante v 3.00 m/s , calcolare la forza elettromotrice indotta
in funzione del tempo, e la corrente nella barretta quando passa per l’origine.
[R: 2 |B | v 2rvt v2t 2 , 0.600 A ]
K
Il tratto HK della barretta funziona da generatore per il circuito. Ai suoi capi si stabilisce
la forza elettromotrice cinetica:
|fem | |B | v (t ) |B | v HK (t )
La circonferenza ha equazione x 2 y 2 r 2 , pertanto esplicitandone l’equazione rispetto
alla y si ha y r 2 x 2 , che permette di trovare la lunghezza della corda HK in
funzione della posizione x :
HK yH yK 2 r 2 x 2
L’ascissa della barretta, che parte dal punto A(r, 0) ha una legge oraria:
x (t ) r vt
E quindi, sostituendo:
|fem | |B | v 2 r 2 x 2 2 |B | v r 2 (r vt )2 2 |B | v 2rvt v 2t 2
Rc
f |B |l v
Rc
R
Per avere la differenza di potenziale ai capi della barretta nell’istante di attraversamento
dell’origine, si impone x (t ) 0 :
V0 |fem(x 0)| |B | v 2 r 2 02 2 |B | v r (2 0.250 3.00 1.20) V 1.80 V
In quell’istante il circuito è equivalente a due semicirconferenze, ciascuna di resistenza:
18
Rc
r
2
(d / 2)
4r
d
2
2.75 108
4 0.120
(0.300 103 )2
1.47
in parallelo fra loro, ed in serie alla resistenza R della barretta. Lo schema di principio del
circuito è riportato in figura. La resistenza equivalente è:
Rc Rc
1
1.47
3.00
RE R
R Rc 2.25
R R
2
2
c
c
Calcoliamo la corrente:
V0
1.80
I
A 0.600 A
RE
3.00
29. In un piano orizzontale, una barretta metallica di argento ( 1.62 108 m ),
avente sezione S 0.250 mm2 , scivola senz’attrito su di un’iperbole equilatera di
H
equazione x 2 y 2 1 (lunghezze in metri), fatta di filo metallico. Il dispositivo è
immerso in un campo magnetico perpendicolare al piano del circuito, d’intensità
|B | 0.400 T . La barretta parte dal punto A con velocità v 2.60 m/s , che si mantiene
B
v
A
costante. Calcolare la forza elettromotrice indotta in funzione del tempo, il suo valore
quando la barretta ha percorso un tratto d 2.00 m , e la resistenza dell’arco d’iperbole
attraversato sapendo che in quell’istante vi scorre una corrente I 2.80 A .
[R: 2 |B | v 2vt v 2t 2 , 5.88V, 1.73 ]
K
Il tratto HK della barretta funziona da generatore per il circuito. Ai suoi capi si stabilisce
la forza elettromotrice cinetica:
|fem | |B | v (t ) |B | v HK (t )
Esplicitandone l’equazione dell’iperbole rispetto alla y si ha y x 2 1 , che
permette di trovare la lunghezza della corda HK in funzione della posizione x :
HK yH yK 2 x 2 1
L’ascissa della barretta, che parte dal punto A(1, 0) ha una legge oraria:
x (t ) 1 vt
E quindi, sostituendo:
|fem | |B | v 2 x 2 1 |B | v 2 (1 vt )2 1 2 |B | v 2vt v 2t 2
Per avere la differenza di potenziale ai capi della barretta nell’istante richiesto si impone
x (t ) (1.00 2.00) m 3.00 m :
|fem(x 3.00)| |B | v 2 3.002 1 2 |B | v 8 (2 0.400 2.60 2.828) V 5.88 V
In quell’istante il circuito è equivalente a due resistenze in serie alla forza elettromotrice,
una delle quali è la R della barretta, e l’altra RA dell’arco di iperbole. Il verso della
corrente è orario per il lettore, dovendo produrre un campo magnetico entrante, a
compensare l’aumento di flusso uscente dal foglio. Lo schema di principio del circuito è
riportato in figura. Calcoliamo R della barretta:
HK
2 3.002 1
0.367
R
1.62 108
S
0.250 106
La resistenza equivalente è:
RE R RA
Inserendo il valore di corrente fornito dal testo e la forza elettromotrice calcolata,
abbiamo:
5.88
f
f I (R RA ) RA R
0.367 1.73
2.80
I
19
f |B |l v
RA
I
R
B
a
H
K
O
30. Una barra di metallo viene fatta scorrere con accelerazione costante a su di una
semicirconferenza metallica con raggio r . Il dispositivo è immerso in un campo
magnetico B perpendicolare al piano del circuito. Fissare un riferimento in cui il centro
della semicirconferenza è nell’origine, e la barretta, parallela alle ascisse, parte ferma
dall’origine. Ricavare la forza elettromotrice nella barra in funzione della quota y .
[R: 2|B | 2ay(r 2 y 2 ) ]
Il tratto HK della barretta funziona da generatore per il circuito. Ai suoi capi si stabilisce
la forza elettromotrice cinetica:
|fem | |B | v(t ) HK (t ) |B | v(y ) HK (y )
Essendo il moto uniformemente accelerato, risulta che velocità e accelerazione sono legate
allo spazio percorso y dall’equazione:
v 2 v02 2ay
v 2ay
La lunghezza della corda HK in funzione della quota y si trova osservando che:
HK x K x H 2x H 2x
L’equazione della circonferenza è x 2 y 2 r 2 , da cui, esplicitando rispetto alla x si ha
x r 2 y 2 , che sostituita dà:
HK 2x 2 r 2 y 2
E quindi risulta:
|fem | |B | v(y ) HK (y ) |B |
B
2ay(r 2 y 2 )
31. Una barretta metallica di massa m scivola senz’attrito su un binario di resistenza
elettrica trascurabile (come quella della barretta), inclinato di un angolo . Le rotaie sono
separate fra loro da una distanza , e collegate nel punto più alto da una resistenza R . Il
dispositivo è immerso in un campo magnetico uniforme B , perpendicolare al piano dei
binari. Calcolare la velocità costante di caduta che la barretta, partendo ferma dal punto
più alto, raggiunge dopo breve tempo, e la corrente nella barretta.
[R: v Rmg sin /|B | 2 2 , I mg sin /|B | ]
B
R
2ay 2 r 2 y 2 2 |B |
Fissiamo un asse delle ascisse sul piano di scivolamento. Lungo tale direzione agisce la
componente della gravità mg sin , e non appena si genera corrente indotta per effetto
dell’aumento del flusso concatenato al circuito causato dal moto della barra, la forza
magnetica FM IL B . Scegliendo come direzione del versore normale quella verso
n̂
FM
I
mg
l’alto, la corrente indotta sappiamo che ha verso orario se vista da un osservatore a cui
punta n̂ . In un disegno che mostra la vista laterale, la corrente nella barretta è diretta
verso il lettore (vedi figura) . La forza FM ha direzione perpendicolare a B e alla barretta,
quindi è diretta lungo il piano inclinato, e per la regola della mano destra punta verso la
sommità. Proiettando lungo i binari queste due forze, dalla seconda legge della dinamica
otteniamo il valore dell’accelerazione:
| FM | mg sin ma
La forza elettromotrice cinetica è f |B | | v | , e la corrente vale:
f
|B | v
I
R
R
Per calcolare il modulo della forza magnetica ci occorre solo il modulo della corrente:
|B | v
|B | 2 2v
| FM | |I || L || B | sin 90 (
)( | B | 1)
R
R
Sostituendo nella seconda legge della dinamica si ha:
20
|B | 2 2v
mg sin ma
R
Mentre la forza di gravità rimane costante, la forza magnetica aumenta d’intensità, e
quando eguaglia la gravità, l’accelerazione diviene nulla, e da quel momento non cambia
più perché anche la forza magnetica rimane costante. Imponendo a 0 si trova il valore
costante di velocità richiesto:
|B | 2 2v
|B | 2 2v
Rmg sin
mg sin 0
mg sin v
R
R
|B | 2 2
Calcoliamo la corrente:
|B | v
|B | Rmg sin mg sin
I
R
R
|B |
|B | 2 2
32. Un disco di metallo di raggio r 30.0 cm ruota con velocità angolare costante,
120 rad/s , immerso in un campo magnetico perpendicolare al piano del disco
stesso, d’intensità |B | 4.00 mT . Calcolare la differenza di potenziale VO VA che
A
B
V
s’instaura fra il bordo del disco e il centro, misurata dal voltmetro V in figura, e stabilirne
il segno utilizzando la forza di Lorentz.
[R: 2.16 mV ]
.
La forza elettromotrice fra A e O è, in valore assoluto, data dal numero di linee tagliate
dal raggio OA nell’unità di tempo:
|B | 12 r 2 1 2
linee tagliate in t
|B | A
fem
|B | r
t
t
t
2
3
0.400 10
B
2
0.300 120
V 2.16 103 V 2.16 mV
2
La forza di Lorentz sposta gli elettroni verso il bordo, quindi il potenziale a cui si A sul
bordo, svuotato di carica negativa, è maggiore del potenziale a cui si trova O, dove gli
elettroni si accumulano. Quindi:
FL
e
v
VO VA 2.16 mV
33. Con riferimento al problema precedente, calcolare la differenza di potenziale VO VA
che in assenza del campo B si produce per gli effetti centrifughi della rotazione.
Suggerimento: considerare elettrone che dal centro raggiunge il bordo del disco, ed
applicare la legge di conservazione dell’energia. Per l’elettrone assumere
e 1.60 1019 C , m 9.11 1031 kg .
[R: 3.69 nV ]
Sull’elettrone al centro del disco compiono lavoro solo forze interne al sistema:
K U (K A KO ) (U A UO ) 0
1
( mv 2 0) (qVA qVO ) 0
2
Ricordando che in un moto circolare uniforme v r :
VA VO
VO VA
1 mv 2
m 2r 2
Quindi:
2 q
2e
m 2r 2
9.11 1031 1202 0.3002
V 3690 1012 V 3.69 nV
19
2e
2 1.60 10
34. Una semicirconferenza di raggio r 25.0 cm , realizzata con del filo di argento
( 1.62 108 m) ha il centro sul bordo di una regione dove c’è un campo magnetico
uniforme, d’intensità |B | 6.00 mT , perpendicolare alla superficie racchiusa dal filo. Il
B
2
circuito ruota con accelerazione angolare costante 5.00 rad/s , partendo fermo
21
O
r
quando l’angolo in figura è nullo. Calcolare la corrente nel circuito nell’istante in cui
vale /2 , sapendo che la sezione del filo misura S 0.280 mm2 . Orientare il
versore normale verso il lettore.
[R: I |B | Sr /( 2) 0.200 A ]
Scegliendo la normale orientata verso il lettore, il verso positivo di percorrenza è quello
che al lettore appare antiorario. La forza elettromotrice e la corrente indotta valgono:
1
(t ) |B | A(t ) cos 0 |B | r 2 (t )
2
L’area A(t ) è quella del settore circolare attraversato dal campo magnetico. La legge
oraria del moto uniformemente accelerato per l’angolo (t ) si scrive:
(t ) 0 0t 1 t 2 1 t 2
2
2
Sostituendo:
1
(t ) |B | A(t )cos 0 |B | r 2 t 2
2
1 2
fem (t ) |B | r (2t ) |B | r 2 t
2
Indicando con R la resistenza della semicirconferenza:
fem
|B | r 2 t
I
R
R
Dalla seconda legge di Ohm possiamo calcolare R ed inserirla:
L
r 2r
r
R
( 2)
S
S
S
2
|B | r t
|B | Sr
I
t
R
( 2)
L’istante in cui /2 è:
1 2
t
t /
2 2
Sostituendo abbiamo:
|B | Sr
|B | Sr
I
( 2)
( 2)
(t )
6.00 103 0.280 106 0.250 3.14 5.00
8
1.62 10 (3.14 2)
A 0.200 10368 A 0.200 A
Il valore negativo indica che I scorre contro il verso scelto come positivo. Dunque la
corrente ha verso orario per il lettore.
A
B
35. Una barretta OC gira con velocità angolare costante 20.0 rad/s strisciando su
C
O
una circonferenza di
raggio r OC 40.0 cm , entrambe di filo
8
di rame
2
( 1.69 10 m) con sezione S 0.320 mm . Perpendicolare al piano della
circonferenza si ha un campo magnetico uniforme, d’intensità |B | 5.00 mT . Il punto A
ed il centro O della circonferenza sono collegati con dei contatti striscianti ed un circuito
di resistenza trascurabile. Dopo aver osservato che per andare da A in O esistono due
percorsi in parallelo, calcolare la differenza di potenziale VA VO ai capi della barretta, la
/2 .
corrente nella barretta in funzione del tempo, e il suo valore quando AOC
[R: 8.00 mV, I S |B | r /[2 t(2 t )],0.174 A ]
In un intervallo di tempo t , il raggio OC ruota di un angolo , spazzando il settore
circolare AOC di area A 12 r 2 . L’area A è attraversata ortogonalmente da un
22
numero di linee di campo che si scrive |B | A , infatti, |B | esprime il numero di linee
per unità di superficie ortogonale ad esse. La forza elettromotrice fra A e O è quindi:
|B | 12 r 2 1 2
linee tagliate in t
|B | A
fem
|B | r
t
t
t
2
3
A
B
2
0.400 20.0
V 8.00 103 V 8.00 mV
2
Per andare da A ad O, la corrente può scorrere lungo l’arco di circonferenza AC, di
5.00 10
C
O
D
resistenza R1 , oppure lungo l’arco ADC, di resistenza R2 . Si tratta di due percorsi in
parallelo, la cui resistenza equivalente è in serie alla resistenza presentata dalla barretta
R3 . Il circuito è quindi equivalente allo schema qui a lato, di resistenza equivalente RE .
La corrente nella barretta è la corrente nel generatore, cioè la corrente nella resistenza
equivalente al circuito:
|B | r 2
fem
I
RE
2RE
Calcoliamo la resistenza dei due archi di circonferenza osservando che all’istante t
l’angolo (t ) spazzato dalla barretta OC, iniziando a misurare il tempo da quando passa
A
fem
R1
R2
R3
per A, segue la legge oraria:
O
(t ) 0 t t
Risulta AC (t ) e ADC 2 (t ) . Sostituendo si ha:
LAC
r AC
r
t
S
S
r
r (2 t )
R2
ADC
S
S
S
Con la formula per le resistenze in parallelo:
r r (2 t )
t
R1R2
r t(2 t )
r
S
R12
S
t (2 t )
R1 R2
r (2 t )
S t (2 t ) 2S
r
t
S
S
Calcoliamo la resistenza della barretta:
L
r
R3 OC
S
S
E quindi la resistenza equivalente al circuito è:
r
r
r
RE R3 R12
t(2 t )
[2 t(2 t )]
S 2S
2S
Da cui:
|B | r 2
|B | r 2
S |B | r
I
2RE
r
[2 t(2 t )]
2
[2 t(2 t )]
2S
Per t AOC /2 risulta:
S |B | r
S |B | r
I
[2 ( /2)(2 / 2)] [2 3 / 4]
R1
S
LADC
6
0.320 10
3
5.00 10
0.400 20.0
1.69 108 [2 3 3.14 / 4]
A 1.74 10638 A 0.174 A
36. Un triangolo equilatero di filo metallico, privato della base, di lato 50.0 cm viene
fatto ruotare attorno ai due contatti girevoli A e C in figura, con velocità angolare costante
12.0 rad/s . Sapendo che la resistenza dell’intero circuito vale R 2.00 , e che il
23
A
C
B
R
dispositivo è immerso in un campo magnetico uniforme come in figura, d’intensità
|B | 0.300 T calcolare la corrente nell’istante in cui è stato compiuto un quarto di giro.
[R: 156 mA ]
L’area spazzata dal triangolo girevole è 43 2 , però il circuito completo comprende
B
anche l’area del rettangolo avente base AC. Tuttavia quest’area è fissa e il flusso
magnetico 0 ad essa concatenato, non varia mai, ma si somma a quello attraverso il
r
t
semicerchio, che è ora positivo, ora negativo a seconda dell’inclinazione.
0 3 2 |B | cos 0 3 2|B | cos t
4
4
Nel calcolare la forza elettromotrice come derivata del flusso, la parte costante scompare:
d
d
0 ( 3 2 |B | sin t ) 3 2 |B | sin t
4
4
dt
dt
e la corrente vale:
V
fem 3r 2 |B |
I
sin t
R
R
4R
Il tempo necessario a percorrere un quarto di giro è un quarto del periodo, cioè:
T
1 2
t1
4
4
2
2
3r |B |
12.0 1.732 0.5002 0.300
I (t1 )
sin
1 A 0.156 A 156 mA
4R
2
4 2.50
fem
a
A
C
B
R
37. Un rettangolo di filo di metallo, aperto da un lato, con dimensioni 40.0 cm ,
a 20.0 cm , viene fatto ruotare attorno ai due contatti girevoli A e C in figura, con
velocità angolare costante 18.0 rad/s . Sapendo che la resistenza dell’intero circuito
vale R 3.20 , e che il dispositivo è immerso in un campo magnetico uniforme come
in figura, d’intensità |B | 0.500 T , calcolare la potenza media da esso dissipata in un
giro. Per il calcolo sfruttare il fatto che il valore medio della funzione sin2 t su di un
periodo è ½.
[R: 162 mW ]
L’area spazzata dal rettangolo girevole è a , mentre il circuito completo comprende
anche l’area del rettangolo di base AC. Tuttavia quest’area è fissa e il flusso magnetico 0
ad essa concatenato, non varia mai, ma si somma a quello attraverso il rettangolo girevole
aperto, che è ora positivo, ora negativo a seconda dell’inclinazione.
0 a |B | cos 0 a|B | cos t
Nel calcolare la forza elettromotrice come derivata del flusso, la parte costante scompare:
d
d
0 ( a |B | sin t ) a |B | sin t
dt
dt
e la potenza dissipata vale:
V 2
fem 2
2 2a 2 |B | 2
P
sin2 t
R
R
R
Il valore medio su di un periodo è quindi:
18.02 0.4002 0.2002 0.500
2 2a 2 |B | 2
W 0.162 W 162 mW
Pmedia
2R
2 3.20
fem
v
b
B
38. Un rettangolo di filo metallico, con dimensioni 50.0 cm e b , di resistenza
complessiva R 25.0 ,
e massa m 160 g ,
avanza a velocità costante
|v | 3.00 cm/s penetrando in una regione in cui si ha un campo magnetico uniforme,
perpendicolare al piano del rettangolo, d’intensità |B | 0.800 T . Sapendo che la regione
24
si estende per una lunghezza maggiore di b , calcolare quanto lungo deve essere b
affinché il circuito si fermi non appena è penetrato per intero nella regione del campo.
[R: 75.0 cm ]
Non appena il rettangolo entra nella regione dove c’è il campo, sul lato davanti si esercita
una forza frenante (verso sinistra rispetto alla figura) d’intensità:
|B | v
|B |2 2v
| FM | |I || L || B | sin 90
( | B | 1)
R
R
La forza agisce finché il rettangolo non è completamento entrato nella regione dove si ha
il campo, perché da quel momento in poi, il flusso magnetico attraverso di esso non
cambia più e la corrente cessa. L’accelerazione del circuito è verso sinistra come la forza.
In un riferimento orientato con le ascisse verso destra vale:
|FM |
|B | 2 2
a
v
m
mR
Scrivendo a v /t e v x /t , e semplificando t si ottiene la relazione:
|B | 2 2
x m v
R
Imponiamo che lo spazio necessario per far arrestare la barretta sia x b e
contemporaneamente imponendo che il cambiamento di velocità v sia quello dal
valore iniziale v finché non si ferma, cioè v 0 v . Sostituendo si ottiene:
|B | 2 2
b m(0 v)
R
b
mvR
0.160 3.00 102 25.0
m 0.750 m 75.0 cm
2 2
|B |
0.8002 0.5002
8
39. Un quadrato di filo di argento ( 1.62 10 m) ,
di lato
v
0 25.0 cm è
immerso in un campo magnetico perpendicolare al piano del circuito, d’intensità
|B | 8.00 mT . La sezione del filo è S 1.40 mm2 . Il campo è uniformemente
B
0
distribuito in una regione anch’essa quadrata, e il filo avanza a velocità costante
|v | 2.00 cm/s in modo che le diagonali dei due quadrati si mantengano sulla stessa
retta, come in figura. Ricavare l’andamento della corrente nel filo metallico in funzione
del tempo durante la fase di uscita dal campo, e rappresentarlo in un grafico.
[R: I (t ) 3.46 ( 2 0.0800t ) mA ]
Scegliamo un versore n̂ che punta al lettore, e di conseguenza un verso di
percorrenza positivo che al lettore appare antiorario.
Il flusso magnetico
concatenato al circuito vale:
(t ) |B | A(t )cos 0 |B | A(t )
dove A(t ) è l’area della porzione di quadrato attraversata dalle linee di campo
all’istante t . Inizialmente A(t ) 20 , ma poi la porzione di circuito immersa nel
campo diviene un quadrato di lato sempre più piccolo, e pari a:
vt
(t ) 0
2
Quindi il flusso vale:
2
vt
0
2
Così che la forza elettromotrice indotta è:
(t ) |B | 2 (t ) |B |
25
v
(t )
B
0
2
vt 2 |B | vt v |B | ( 2v v 2t )
0
0
0
2
2
2
La corrente nel quadrato di filo si trova calcolando la resistenza tramite la seconda legge
di Ohm:
4
L
R 0
S
S
fem
I (t ) [mA]
3.46 2
0.277
t[s]
I (t )
d
d
|B |
dt
dt
fem
|B |
R
8.00 103
2v 0 v 2t
4 0
vS
v
S |B |
( 2 t)
4
0
2.00 102 1.40 106
4 1.62 108
( 2
2.00 102
t)
0.250
3.46 103 ( 2 8.00 102 t ) A 3.46 ( 2 0.0800t ) mA
R
0
0
vertice di una regione anch’essa quadrata di lato 0 , in cui c’è un campo magnetico
uniforme, d’intensità |B | 0.200 T , perpendicolare alla superficie racchiusa dal filo. Il
circuito ruota con velocità angolare costante 2.50 rad/s , partendo fermo quando i
lati dei due quadrati coincidono. Ricavare l’andamento della fem nel circuito in
funzione del tempo finché i due quadrati non sono esattamente sovrapposti. Calcolare il
valore della resistenza R sapendo che nel momento della sovrapposizione la corrente
vale 55.0 mA . Scegliere il versore normale entrante nel foglio.
[R: |B | 20/2 cos2 (t /2),1.84 ]
B
R
0
0
A
40. Un quadrato di filo metallico di lato 0 45.0 cm ha un vertice coincidente col
C
Scegliendo la normale orientata in modo da allontanarsi dal lettore, il verso positivo di
percorrenza è quello che al lettore appare orario. La forza elettromotrice e la corrente
indotta valgono:
(t ) |B | A(t ) cos180 |B | A(t )
Chiamiamo C AE
(t ) , per t 0 si ha (t ) 0 . Misuriamo l’angolo in verso orario.
Fintanto che i due quadrati non sono perfettamente sovrapposti per (t ) /2 , l’area
B
D
E
A(t ) che contribuisce al flusso aumenta, ed è quella di due volte il triangolo rettangolo
ACD di cateto maggiore AC 0 e cateto minore CD 0 tan 1 (t ) . La legge oraria
2
del moto uniformemente accelerato per l’angolo (t ) si scrive:
(t ) 0 t t
Quindi:
1
A(t ) 2 0 0 tan 12 (t ) 20 tan 12 t
2
Sostituendo:
(t ) |B | A(t ) |B | 20 tan( 1 t )
2
Calcoliamo la derivata del flusso concatenato per avere la forza elettromotrice:
2
1
2
|
B
| 0
d
2
2
fem (t ) |B | 0 tan( 1 t ) |B | 0
2
2
1
dt
cos ( 2 t ) 2 cos2 (t / 2)
La corrente è legata alla forza elettromotrice dalla prima legge di Ohm:
|B | 20
fem
I
R
2R cos2 (t /2)
Quando i due quadrati sono sovrapposti, l’angolo è (t ) /2 t . Sostituiamo ed
imponiamo il valore di corrente fornito, così da trovare R :
26
R
|B | 20
2I cos2 (t /2)
0.200 0.4502 2.50
2 0.0550 cos2 ( / 4)
1.84
41. Una barretta metallica di lunghezza 0 50.0 cm , scivola senz’attrito, alla velocità di
2.50 m/s , su di un binario orizzontale, mantenendo sempre un’inclinazione 60 . Le
rotaie hanno resistenza trascurabile, e sono collegate da tre resistori come in figura, di
valori R1 1.00 , R2 3.00 ed R3 6.00 . Il dispositivo è immerso in un campo
magnetico uniforme, perpendicolare al piano del circuito, d’intensità |B | 0.400 T .
R2
R1
B
R3 0
v
Calcolare la differenza di potenziale ai capi della barretta e la corrente che scorre in R3 ,
sapendo che la resistenza della barretta vale RB 5.00 .
[R: 433 mV(+in alto), 26.0 mA(dal basso in alto) ]
Le due resistenze in serie possono essere sostituite dalla loro resistenza equivalente:
R12 R1 R2 (1.00 3.00) 4.00
B
L’area A(t ) spazzata dalla barretta nel tempo t è un parallelogramma di base vt ed
R12
altezza h 0 sin 60 0 23 e pertanto vale:
vt
R3 0
A(t ) 0 3 vt
2
Scegliendo il versore normale che punta al lettore, il verso di percorrenza positivo è
antiorario. Calcoliamo il flusso magnetico concatenato al circuito e la forza elettromotrice:
(t ) |B | A(t ) cos 0 |B | 0 3 vt
2
d
fem (t ) |B | 0 3 vt |B | 0 3 v
2
2
dt
(0.400 0.500 3 2.50)V 0.433 V
2
Il valore negativo indica che la corrente prodotta da questa fem ha verso orario per il
lettore. Il circuito equivale ad un generatore e tre resistenze disposte come in figura, e che
sono il parallelo di R12 ed R3 , posto in serie ad RB . Calcoliamo dapprima la corrente in
RB , che è la stessa che scorre nella resistenza equivalente al circuito:
RE RB
4.00 6.00
7.40
5.00
R12 R3
4.00 6.00
R12R3
f
0.433
A 0.0585 A
RE
7.40
IB
Questa corrente entra nel partitore di corrente formato dal parallelo di R12 ed R3 , e si
separa in due correnti I 12 I 3 I B inversamente proporzionali alle resistenze. Quindi:
I3
I 12
R12
R3
Ricavando I 12 I B I 3 ed inserendo:
I3
R12
R3
I 12
R12
R3
(I B I 3 )
I 3 (1
R12
R3
)
R12
R3
IB
4.00
A 0.0260 A 26.0 mA
0.0585
R3 R12
5.00
4.00
Il segno meno in questo caso indica che la corrente rispetto alla figura è dal basso verso
l’alto.
I3 IB
R12
27
R12
R3
f
RB
42. Una barretta metallica di lunghezza 75.0 cm ,
C
F
B
e massa m 250 g scivola
senz’attrito su di un binario orizzontale, tirata verso destra da una forza costante
d’intensità |F | 3.00 N , muovendosi di moto uniformemente accelerato nel verso della
forza. Le rotaie hanno resistenza trascurabile, e sono collegate fra loro da un condensatore
di capacità a tre resistori come in figura, di valori C 800 mF . Il dispositivo è immerso
in un campo magnetico uniforme, perpendicolare al piano del circuito, d’intensità
|B | 0.900 T . Calcolare l’accelerazione della barretta. Spiegare in cosa si trasforma il
lavoro della forza F .
[R: 4.88 m/s2 , Kbarra e UC ]
Come sappiamo dalla definizione di capacità, la carica sul condensatore è legata in ogni
istante alla differenza di potenziale VC (t ) fra le sue armature dalla relazione:
Q(t ) C VC (t )
E quindi sostituendo nella definizione di corrente I Q (t ) e osservando che, nella
derivata rispetto al tempo, C è solo una costante moltiplicativa:
I Q (t ) CVC (t )
In base alla legge di Ohm, la differenza di potenziale fra le armature del condensatore è
uguale alla forza elettromotrice indotta dovuta al moto della barretta. La forza
elettromotrice cinetica vale:
| fem | |B | v(t ) VC (t )
Ricordando ora che l’accelerazione è la derivata della velocità, abbiamo:
I CVC (t ) C |B | v C |B | a
Per calcolare il modulo della forza magnetica ci occorre solo il modulo della corrente:
| FM | |I || L || B | sin 90 (C |B | a )( | B | 1) C |B | 2 2a
Possiamo infine ricavare l’accelerazione sostituendo | FM | nella seconda legge della
dinamica:
| FM | | F | ma
a (C |B | 2 2 ) | F | ma
|F |
3.00
a
m/s2 4.88 m/s2
2 2
m C |B |
0.250 0.800 0.9002 0.7502
Il lavoro della forza viene convertito in energia cinetica della barretta ed energia
potenziale elettrostatica accumulata nel condensatore.
43. In un campo magnetico verticale uniforme, d’intensità |B | 0.300 T , avanza con
velocità costante |v | 1.20 m/s lungo un piano orizzontale un anello metallico
A
v
B
semicircolare, di raggio r 25.0 cm . Calcolare la differenza di potenziale fra i capi A e
C, stabilendo quale dei due è a potenziale maggiore.
[R:VC VA 0.180 V ]
C
La differenza di potenziale VA VC è uguale alla forza elettromotrice cinetica generata in
FL
e
B
v
una barretta conduttrice immaginaria, che unisce A con B. Sappiamo, infatti, che la
barretta e la semicirconferenza tagliano lo stesso numero di linee di campo al secondo,
perché si mantiene costante il flusso magnetico attraverso il conduttore chiuso formato
dal semi-anello e dalla barretta. Così come lo stesso numero di linee al secondo è tagliato
da un conduttore di qualunque forma che unisca A e B. La forza di Lorentz sugli elettroni
della barretta è diretta verso A, dove si ha quindi un accumulo di carica negativa.
Pertanto VC VA 0 e inoltre:
VC VA fem |B | |v | AC |B | |v | 2R (0.300 1.20 2 0.250) V 0.180 V
28
x
44. Un quadrato di filo metallico di lato HK 90.0 cm , massa m 75.0 g e
resistenza R 4.00 , cade lungo un piano verticale, in una zona di campo magnetico
orizzontale. Orientando le y come in figura, l’intensità del campo cresce procedendo
verso il basso, seguendo la legge B(y ) B0y , con B0 0.800 T/m . Rappresentare un
circuito equivalente al dispositivo, e individuare il verso della corrente indotta e della
forza magnetica complessiva. Mostrare che dopo una fase iniziale, l’accelerazione del
circuito diviene nulla, ed esso cade ad una velocità limite, costante, di cui si chiede il
valore. Calcolare la corrente indotta e la forza magnetica in questa situazione.
[R: I B0v 2 /R, |FM | B02v 4 /R, vL Rmg /B02 4 7.00 m/s, 0.736 N, 1.42 A ]
Durante la caduta, solo i lati HK ed MN tagliano le linee del campo. Solo essi pertanto
generano due forze elettromotrici cinetiche, aventi lo stesso verso, cioè con il positivo a
destra. Infatti, gli elettroni nel tratto HK ed MN hanno velocità in basso e quindi
subiscono una forza di Lorentz verso sinistra. Il verso della corrente prodotta da questi
due generatori contrastanti, si può dedurre prima di fare il calcolo, osservando che il
flusso entrante nel piano del foglio aumenta man mano che il quadrato si sposta in basso.
Occorre quindi una corrente indotta che produca un campo magnetico uscente dal foglio,
cioè antioraria vista dal lettore. Questa deduzione trova conferma nel fatto che la forza
elettromotrice indotta nel tratto MN è maggiore di quella indotta nel tratto HK. Infatti:
fHK |B | | v | HK B0yH v(t )
fMN |B | |v | MN B0yM v(t )
H
y
F
H L e
B
B0v
N
v
H
Il segno meno indica che la forza magnetica risultante complessiva è diretta in basso.
Scrivendo la seconda legge della dinamica abbiamo:
|FHK | |FMN | mg ma
B02 4
R
Ragionando sull’equazione ottenuta si vede la velocità v , inizialmente nulla, aumenta in
modo uniforme a causa della gravità, ma l’aumento è contrastato dalla forza magnetica,
tanto maggiore quanto più grande è v . Non appena la velocità raggiunge quel valore per
cui forza magnetica e forza di gravità sono uguali, l’accelerazione si annulla. Da quel
momento la velocità resterà costante. Indichiamo con vL , questo valore, detto velocità
limite. Imponendo a 0 si trova:
vL
Rmg
B02 4
4.00 0.0750 9.81
0.8002 0.900 4
m/s 7.00 m/s
A cui corrisponde:
29
K
R
M f
MN
H
I
B
M
v mg ma
fHK
I
2
R
R
La forza magnetica su HK è quindi diretta in basso (positiva nel nostro riferimento),
quella su MN in alto (negativa). Su tratti HM e KN le due forze magnetiche sono uguali
ed opposte, data la simmetria del campo in direzione orizzontale, e si annullano.
Sommando i due contributi si ha:
2 4
B v 2
B () B0 v
|FHK | |FMN | I BH I BM I B0 (yH yM ) 0
0
R
R
v
M
Avendo sfruttato che nel nostro riferimento si ha yM yH . Per la corrente si ha:
K
FL e
elettromotrice complessivamente indotta nel quadrato è allora:
fMN fHK |B | | v | HK B0v yM yH B0v yM B0v (yM yH ) B0v 2
fMN fHK
N
v
M
Scegliendo come positivo il verso della corrente che appare antiorario al lettore, si ha
fMN 0 perché tende a far scorrere la corrente in tale verso, e fHK 0 . La forza
I
K
N
FHK
K
FMN
I
N
B 2 4 Rmg
|FHK | |FMN | 0
mg (0.0750 9.81) N 0.736 N
R B 2 4
0
Cioè la forza magnetica diviene uguale alla gravità, nel caso limite, e per la corrente:
I
B
R
B0 2 Rmg
mg
0.0750 9.81
A 1.42 A
2
R B 2 4
B0
0.8002 0.9002
0
45. Una barretta di lunghezza 1.20 m , di massa e resistenza trascurabili, scorre
senz’attrito in un piano orizzontale, sopra a due rotaie conduttrici di resistenza
trascurabile, collegate da un resistore R 2.00 . La barretta è tirata da un filo ideale,
che passa per la gola di una puleggia ed ha una massa pendente m 150 g agganciata
m
all’altro estremo. Il dispositivo è immerso in un campo magnetico uniforme, verticale,
d’intensità |B | 0.700 T . Ricavare la tensione del filo in funzione della velocità v(t ) della
barretta. Mostrare che, dopo una fase iniziale, l’accelerazione della barretta diviene nulla,
e viene raggiunta una velocità limite vL , costante, di cui si chiede il valore.
[R: |T | |B |2 2v(t )/R, 4.17 m/s ]
La barretta è tirata verso destra dalla tensione del filo T e verso sinistra dalla forza
magnetica. Le intensità delle due forze sono uguali, essendo nulla la massa della barretta:
|FM | |T | max 0 ax 0
|T | |FM |
La forze elettromotrice cinetica generata dalla barretta, e la corrente nella resistenza sono:
|B | v(t )
f
f |B | v(t ) I
R
R
La forza magnetica (verso sinistra), e quindi la tensione (verso destra), valgono:
|B | v(t )
|B |2 2v(t )
|FM | I |B |
|B |
|T |
R
R
Per trovare l’accelerazione dobbiamo scrivere le equazioni della dinamica per la massa
pendente:
|T | mg ma
Ragionando sull’equazione ottenuta si vede la velocità v , inizialmente nulla, aumenta in
modo uniforme a causa della gravità, ma l’aumento è contrastato dalla forza magnetica,
tanto maggiore quanto più grande è v . Non appena la velocità raggiunge quel valore per
cui forza magnetica e forza di gravità sono uguali, l’accelerazione si annulla. Da quel
momento la velocità resterà costante. Indichiamo con vL , questo valore, detto velocità
limite. Imponendo a 0 si trova:
|T | mg 0
vL
A
H
E
v
K
R2
|B | 2 2vL
R
mg
mgR
0.150 9.81 2.00
m/s 4.17 m/s
2 2
|B |
0.7002 1.202
46. Una barretta orizzontale HK ha resistenza trascurabile, lunghezza 1.30 m , e
massa m 150 g . Essa scorre senz’attrito lungo due rotaie conduttrici, verticali, AE e
R1 C
B
|T | mg
D
CD, di resistenza trascurabile, collegate ai due estremi dalle resistenze R1 2.00 ,
R2 3.00 come in figura. Il dispositivo è immerso in un campo magnetico orizzontale,
perpendicolare al piano del circuito, d’intensità |B | 0.800 T . Rappresentare il
dispositivo con un circuito equivalente, e calcolare la velocità limite e la potenza dissipata
quando la discesa avviene alla velocità limite.
[R: 1.77 m/s,2.81 W ]
La fem cinetica indotta nella barretta alla velocità limite vale:
30
f |B | |v L |
Il dispositivo equivale ad un circuito come quello rappresentato qui a lato. Il polo positivo
del generatore è dalla parte di K perché la forza di Lorentz sposta gli elettroni verso H. Le
due resistenze sono fra loro in parallelo, quindi la corrente I nella barretta vale:
R1R2
2.00 3.00
RE
1.20
R1 R2
2.00 3.00
|B | |v L |
f
I
RE
RE
La velocità limite si raggiunge quando la forza magnetica sulla barretta |FM | I |B |
R1 C
A
f
H
K
I
E
D
R2
uguaglia la forza di gravità. Da questa condizione possiamo ricavare la corrente nella
barretta:
|B | |v |
mgR
L
|B | mg
I |B | mg
|vL | E
RE
|B |2 2
mgR
0.150 9.81 1.20
|v L | E
m/s 1.766 m/s
2 2
|B |
0.8002 1.302
Quindi possiamo ora calcolare la potenza dissipata dal circuito:
|B | 2 |vL | 2 2
f2
0.8002 1.7662 1.302
P
W 2.81 W
RE
RE
1.20
47. Un rettangolo ACDE è fatto di un filo metallico, avente base ED 75.0 cm ,
altezza AE 23 , diviso da un collegamento FG in modo che EG /3 . Il tratto di
filo ED ha resistenza R 1.00 . Il dispositivo è immerso in un campo magnetico B(t )
perpendicolare al piano del rettangolo, d’intensità uniforme, ma crescente nel tempo in
ragione di 50.0 mT/s . Ricavare la forza elettromotrice in ciascuna delle maglie FAEG e
FGDC, disegnare il circuito equivalente e calcolare la corrente nei rami FAEG, FG, FCDG.
[R: 4.99 mA,6.07 mA,1.08 mA ]
A
F
C
E
B(t )
G
D
Scegliamo la normale verso il lettore, e quindi il verso di percorrenza positivo del circuito
è in senso antiorario per chi legge. Il flusso 1 concatenato alle maglie AFGE e il flusso
2 concatenato alle maglie FCDG valgono rispettivamente:
1 EG AE |B(t )| cos180 13 23 |B(t )| 29 2 |B(t )|
2 GD AE |B(t )| cos180 2 2 |B(t )| 4 2 |B(t )| 21
A
Per il calcolo della forza elettromagnetica osserviamo che il dato del testo sulla velocità di
variazione del campo magnetico equivale a:
d |B(t )|
50.0 mT/s 50.0 103 T/s
dt
E
3
3
F
C
I1
I2
9
Dalla legge di Faraday-Neumann:
2 0.7502 50.0 103
2 d |B(t )|
2
fem1 1 1 9
V 6.25 mV
dt
9
A
fem2 2 21 12.5 mV
Il verso delle correnti in entrambe le maglie FAEG e FCDG dev’essere antiorario per il
lettore, in quanto deve produrre un campo uscente dalla pagina, per compensare
l’aumento del flusso magnetico entrante nella pagina. Pertanto il dispositivo equivale al
circuito qui a lato raffigurato. Calcoliamo ora le resistenze di ciascun tratto. Se chiamiamo
31
G
R1
D
R2
F
f1
C
R3
f2
E
G
D
R1 la resistenza dell’intero ramo FAEG, R2 la resistenza dell’intero ramo FCDG, ed R3
A
R1
f1
R3
I1
E
R2
F
G
I3
I2
quella del ramo FG, si ha:
4
1
R1 R , R2 2R , R3 R
C
3
3
Indicando
con
I
la
corrente
nel ramo FG, supponendola da F verso G, possiamo
3
risolvere il circuito applicando i principi di Kirchhoff.
f2
Maglia FAEG percorsa in senso antiorario, cadute di potenziale:
R1I 1 f1 R3 I 3 0 (1)
D
Maglia FGDC percorsa in senso antiorario, cadute di potenziale:
R3I 3 f2 R2I 2 0 (2)
Nodo F:
I 2 I1 I 3
(3)
Ricavando I 3 I 2 I1 dall’equazione (3) ed inserendola nella (2) e nella (1) si ha il
sistema:
R I f R (I I ) 0
I (R R ) R I f 0
11
1
3 2
1
3
3 2
1
1 1
R3 (I 2 I 1 ) f2 R2I 2 0
R3 I1 I 2 (R2 R3 ) f2 0
Sostituendo i valori delle resistenze:
5 RI 1 RI f
5I 1 I 2 3f1 /R
5(7I 2 3f2 /R) I 2 3f1 /R
3 1 3 2
1
1
7
RI RI f
I 1 7I 2 3f2 /R
I 1 7I 2 3f2 /R
2
3 1 3 2
34I 2 3(f1 5f2 )/R
I 3(f1 5f2 )/ 34R
2
I 1 7I 2 3f2 /R
I 1 7I 2 3f2 /R
I 3(f 5f )/ 34R [3(6.25 5 12.5)/ 34] mA 6.07 mA
2
1
2
I 1 7I 2 3f2 /R (7 6.07 3 12.5) mA 4.99 mA
I 3 I 2 I 1 (6.07 4.99) mA 1.08 mA
32