Simulazione Nazionale di Fisica – 11 Marzo 2015

Simulazione Nazionale di Fisica – 11 Marzo 2015 - INDUZIONE
Possibile svolgimento
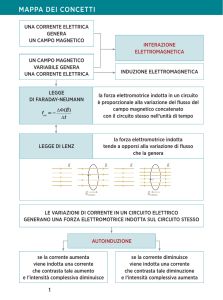
1. Luigi vuole generare una tensione alternata muovendo opportunamente un circuito elettrico
all’interno di un campo magnetico uniforme. La superficie attraversata dal campo magnetico varia
nel tempo poiché parte del circuito è collegata ad una molla ed è pertanto possibile applicare la
legge di Faraday Neumann Lenz per determinare l’intensità di tale d.d.p, nota la resistenza elettrica
del circuito.
Prima di collegare la resistenza tra i due poli, nel circuito non circola corrente e quindi la barretta è
soggetta alla sola forza elastica. Si muove di moto armonico con equazione
𝑥 = 𝑎𝑐𝑜𝑠(2𝜋𝑓𝑡)
dove con x si indica la posizione della barretta, con 𝑎 l’ampiezza massima del moto, con 𝑓 la
frequenza dell’oscillazione e con 𝑡 l’istante di tempo.
La frequenza di oscillazione è data da
𝑓=
1 𝑘
√
2𝜋 𝑚
Sostituendo i dati forniti dal testo si ottiene
𝑘 = (2𝜋𝑓)2 ⋅ 𝑚 = (2𝜋 ⋅ 50)2 ⋅ 2 ⋅ 10−2 = 1,97 ⋅ 103 𝑁/𝑚
2. Per la presenza del campo magnetico, il moto della barretta genera una forza elettromotrice
indotta proporzionale alla variazione di flusso attraverso la superficie delimitata dalla guida e dalla
barretta. Assumendo come verso del campo magnetico quello uscente dal piano del foglio (asse +z),
il flusso Φ del campo magnetico attraverso la superficie rettangolare delimitata dalla guida e dalla
barretta è dato da:
Φ = 𝐵 ⋅ 𝑆 = 𝐵 ⋅ 𝐿 ⋅ (𝑑 + 𝑥)
Sostituendo con l’espressione di x trovata in precedenza si ha:
Φ = 𝐵 ⋅ 𝑆 = 𝐵 ⋅ 𝐿 ⋅ [𝑑 + 𝑎𝑐𝑜𝑠(2𝜋𝑓𝑡)]
Per la legge di Faraday-Neumann-Lenz la forza elettromotrice indotta f.e.m. è pari a:
𝑓. 𝑒. 𝑚. = −
𝑑Φ
= −𝐵𝐿 ⋅ [−𝑎 ⋅ 2𝜋𝑓 ⋅ 𝑠𝑒𝑛(2𝜋𝑓𝑡)] = 𝑎𝐵𝐿 ⋅ 2𝜋𝑓 ⋅ 𝑠𝑒𝑛(2𝜋𝑓𝑡)
𝑑𝑡
La f.e.m. massima ha pertanto valore pari a
𝑓. 𝑒. 𝑚.𝑚𝑎𝑥 = 𝑎𝐵𝐿 ⋅ 2𝜋𝑓 = 1,0 ⋅ 10−2 ⋅ 0,30 ⋅ 1,0 ⋅ 10−1 ⋅ 2 ⋅ 𝜋 ⋅ 50 = 94,2 𝑚𝑉
⃗⃗ × 𝐵
⃗⃗ il cui effetto è quello di una forza frenante in
3. La barretta subisce l'azione di una forza 𝐹⃗ = 𝑖𝐿
quanto il verso è opposto a quello della velocità istantanea. Infatti, nell’ipotesi fatta per il verso di B
(uscente dal foglio, lungo +z), quando 𝑣 > 0 (cioè la barretta si muove verso destra) allora la forza
elettromotrice farà circolare la corrente in senso orario. La corrente nella sbarretta sarà lungo –y e
quindi la forza F lungo – x (verso sinistra), cioè in verso opposto alla velocità.
4. La barretta si muove quindi sotto l’azione della risultante che si ottiene sommando vettorialmente
la forza elastica e la forza frenante. Il moto risultante è un moto armonico smorzato. La differenza
di potenziale tra i terminali è proporzionale alla velocità 𝑣 = 𝑑𝑥/𝑑𝑡.
5. Dal punto di vista energetico la forza frenante F agente sulla barretta compie un lavoro negativo,
in quanto ha verso opposto allo spostamento. L’energia cinetica della barretta diminuisce nel tempo
e così anche la velocità. Se diminuisce la velocità diminuisce anche la forza elettromotrice indotta e
quindi la corrente indotta. La barretta si fermerà e la forza elettromotrice indotta si annullerà.
La potenza dissipata dalla forza F frenante risulta pari a :
𝑃𝐹 = |𝐹 ⋅ 𝑣| = 𝑖𝐿𝐵𝑣
mentre la potenza dissipata nella resistenza R è data da
𝑃𝑅 = 𝑖 ⋅ 𝑓. 𝑒. 𝑚 = 𝑖𝐿𝐵𝑣
Il lavoro compiuto dalla forza F resistente nell’unità di tempo (ovvero la potenza) è eguale alla
potenza dissipata per effetto Joule dalla corrente indotta nella resistenza R. Quindi il generatore di
Luigi non funziona in modo ideale per la produzione di corrente alternata, limitandosi a dissipare
per effetto Joule l’energia inizialmente fornita alla barretta.
Problema (variante sul tema)
Considera un apparato fisico simile a quello dell’esercizio precedente. La molla ha costante elastica
pari a 3000 N/m. Quale deve essere la massa collegata alla molla affinché si generi una corrente
alternata a 50 Hz?
[30,4 g]
Sapendo che l’ampiezza dell’oscillazione è pari a 2 cm, la barretta è larga 20 cm e il campo
magnetico ha intensità pari a 200 mT, rappresenta in un piano cartesiano l’andamento della fem in
funzione del tempo trascurando attriti ed effetti dissipativi. Qual è il valore massimo della fem?
[251 mV]
Supponi che l’estremità fissa della molla sia ora agganciata a destra del circuito. Come variano i
risultati sopra indicati? Si hanno variazioni dal punto di vista energetico rispetto all’esercizio
precedente?