Emissione gamma - INFN

Revisione Maggio 2012
Emissione Gamma
Formule preliminari
1 – Lunghezza d’onda di un raggio gamma di 1 MeV:
px ≈  per il principio di indeterminazione di Heisenberg o anche dato che per fotoni è E = pc:

c
p ≈  quindi ≈

= 197 MeV fm / 1 MeV = 197 fm
E / c E
2 – Larghezza energetica di un livello nucleare eccitato:
c
197 MeVfm
≈  e quindi 
=
c
3x10 14 fm
 (ns)
ns
per  1 ps = 10-3 ns abbiamo 0.66 10-3 eV.
3 – Energia di rinculo di un nucleo che emette un raggio gamma da 1 MeV, m = A=100:
pnucleo = p con |p = E/c
2
E
12
2
Erinculo = p /2m =
≈
= 5 eV
2 x100 x1000
2mc 2
[Per raggi gamma da 0.1 MeV sara’
Erinculo = 0.05 eV ( >> possibile del livello del caso sopra considerato)]
4 – Energia del decadimento gamma da un livello iniziale di energia Ei a un livello finale Ef
E = Ei -Ef , energia cinetica del nucleo di massa M che rincula Er = pr2 /2M, E = c p
conservazione dell’energia: E = E+ Er
conservazione dell’impulso: |ppr|
si ha equazione di secondo grado: E = E + E / 2M c2


E 

le cui soluzioni sono: E = Mc2  1   1  2
2 
Mc



La soluzione negativa e’ ovviamente da scartare perche’ non fisica e
1
1
sviluppando in serie la radice al 2 ordine ( 1  x  1  x  x 2 + ...)
2
8
2
(E )
si ottiene E
e quindi con ottima approssimazione, considerato anche che la
2Mc 2
risoluzione sperimentale ottenibile con rivelatori gamma è dell’ordine del keV, e’
E≈praticamente per tutte le transizioni gamma.
(E ) 2
[Inoltre per esempio per E = Ei -Ef = 1 MeV e M = 100,  E
≈eV da confrontare con il valore
2Mc 2
per  1 ps = 10-3 ns della larghezza del livello 0.66 10-3 eV calcolato sopra]
5 – L’effetto Moessbauer
Dai conti fatti, si vede che l’energia presa dal nucleo emettitore a seguito del suo rinculo e’
maggiore praticamente sempre per tutti i casi realistici della larghezza del livello che emette gamma.
Ne segue che poichè il raggio gamma ha di conseguenza una energia (un po’) minore di quella del
livello emettitore (vedi anche dopo) , non si sovrappone alla larghezza naturale del livello e quindi
non corre (per fortuna) il rischio di essere subito riassorbito dal nucleo che lo riemetterebbe in un
ciclo INFINITO !!!
Se poi abbiamo un emettitore gamma e vogliamo che detto gamma vada a eccitare un nucleo
uguale questo non sara’ mai possibile perche’ ci manca un po’ di energia.
Questo puo’ essere compensato (effetto Moessbauer) in due modi:
a) legando se possibile il nucleo emettitore ad una struttura cristallina che assorbirebbe in toto
l’impulso
b) facendo variare la velocita’ del nuleo emettitore il cui gamma grazie all’effetto Doppler puo’
guadagnare proprio la piccola energia mancante. A conti fatti si ottengono delle velocita’ realistiche
realizzabili in laboratorio
A titolo di esempio:
E v
 v


E  E 0 1  cos   che per  0º diventa
E0 c
 c

per gamma da 100 keV di cui sopra si ha: v = c 0.05 eV / 100 keV ≈ 150 m/sec.
Probabilita’ di emissione nelle transizioni e.m.
Un tipico esempio di decadimento gamma.
3.30 MeV
47%
2.13 MeV
E2
2+
165 fs
M1+E2 +
2
fs
53%
E2
0+
0 MeV
34
S
Il punto di partenza e’ l’osservazione che i raggi gamma di diseccitazione nucleare sono di
natura elettromagnetica per cui l’inizio della trattazione, con un approccio semiclassico, e’ quello
delle emissione delle onde elettromagnetiche da una opportuna sorgente che puo’ essere costituta
solo da una distribuzione di cariche in moto descrivibile da un densita’ di corrente variabile nel
tempo.
Iniziamo considerando il caso di un dipolo elettrico, per semplicita’, dato il tipo di corso
istituzionale rimandando a testi piu’ specializzati i casi di multipoli magnetici ed elettrici di ordine
superiore al dipolo.
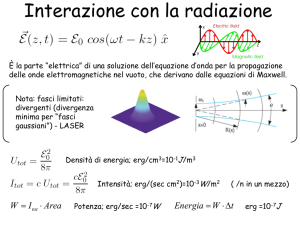
Dalla trattazione delle onde elettromagnetiche derivata dalle equazioni di Maxwell risulta
che grandi distanze r il campo elettrico E di un dipolo elettrico di ampiezza massima statica p che
oscilla con la pulsazione lungo l'asse polare z, nell’ipotesi agggiuntiva che la lunghezza d’onda
emessa sia >> delle dimensioni “a” del dipolo p, [e cioe’ r>>>>a] e’ quello di un’onda sferica
uscente trasversale, cioe’ solo con la componente  ed e’ dato da :
p sin   2 1
E=
sin( kr  t ) con k= 2/e  2/T, c = /T
40 c 2 r
La formula e’ abbastanza simile a quella del campo statico di un dipolo elettrico
p sin  1 1
E=
40 r 2 r
(nota 1: il campo magnetico B ha solo la componente normale ad E lungo .= E/c come si ricava dalle equazioni
di Maxwell
nota 2: nell’equazione il termine (/c)2 = (2 sostituisce il termine 1/r2 che compare nel campo statico del dipolo.
Il modo di ricavare questo termine esula da questa trattazione semplificata.
nota 3: La origine del termine t , la cui dimostrazione comporta MOLTI calcoli, si puo’ grossolanamente motivare
dal fatto che a queste grandi distanze i campi generati dal sistema oscillante non arrivano subito ma ovviamente hanno
bisogno del tempo necessario dalla velocita’ finita delle onde, = c, per arrivare t = r/c. Sono cioe’ dei campi cosiddetti
ritardati).
Ricordando che la densita’ di volume di energia (elettr.+magne.) e’ data da E2 si ha che la
intensita’ dell’onda e.m. (energia trasportata per unita’ di tempo e di superficie), mediata sul tempo,
e’ data da:
1
1
p 2 sin 2   4 1
2
I =  0 cE   0 c
2
2
(40 ) 2 c 4 r 2
Per ottenere tutta l’energia trasportata per unita’ di tempo a grandi distanze dal dipolo bisogna
integrare I in dS = r2sindd. Approssimativamennte basta moltiplicare per la superficie della
sfera 4r2 e approssimare a cioe’ un’onda piana uscente dal dipolo.
Per cui alla fine si ha che la potenza P emessa dal dipolo (energia per unita’ di tempo) e’ data da:
p2  4
P=
(n.b. il coefficiente 12 al denominatore viene dall’integrazione esatta). Per un
120 c 3
dipolo magnetico oscillante la formula e’ analoga con il dipolo magnetico al posto di quello
elettrico (coefficienti dimensionali a parte).
Dopo di che approssimativamente e’
p2 3 1
P
Probabilita’ di transizione = 1/ =



120 c 3 
Nel caso piu’ generale di un multipolo di ordine L (per il dipolo L=1) il campo elettrico e quello
magnetico hanno espressioni assai piu’ complesse come si ricava dalle equazioni di Maxwell. In
modo schematico ed un po’ approssimato le funzioni che descrivono i campi sono soluzioni
dell’equazioni scalare di Helmolz
u + k2 u = 0
[con  
che sono date dalle funzioni uLM = CL jL (kr) YLM ( , con CL costante di normalizzazione.
Le jL(kr) sono le funzioni di Bessel sferiche che all’origine, cioe’ per kr → 0, sono approssimate da
(kr) L
jL (kr) →
(2 L  1)!!
kr<< 1, cioe’ r<<, e’ nel nostro caso una approssimazione assai realistica dato per gamma di circa 1 MeV abbiamo
≈ 200 fm, e con r si intende la dimensione nucleare R cioe’ attorno a 10 fm,
Al posto di p2 bisognera’ inserire il campo attorno a r = 0 per cui in modo approssimato in questo
caso si puo’ scrivere
2
L

1  1   2   
1
2
 2  r 
I =  0c
e YLM
2  40  c  c  (2 L  1)!! 
2
2
viene in realta’ dalla normalizzazione della funzione d’onda del
c2
campo elettrico, alla fine si ottiene la formula seguente:
n.b. il termine aggiuntivo
2 L2
2( L  1)
 
c 
( M (L)) 2
2 
 o L[( 2L  1)!!]  c 
M(L) e’ l’intensita’ del multipolo dal quale e’ emessa la radiazione
[vedi anche lo sviluppo in multipoli descritto in seguito].
nel caso quantistico il multipolo e’ sostituito con l’elemento di matrice:
*
M(L) = | f | er LYLM | i |2 . =  f m(L) i dV con m(L) = erLYLM(
P=

la probabilita' di transizione per unita’ di tempo cioe’ la vita media della transizione gamma e’
quindi data dalla formula:
2 L 1
P
2( L  1)
 
2
 

 (M (L))
2 
  o L[( 2 L  1)!!]   c 
Nel caso magnetico l’operatore ha la forma
 1
m(L) = e
[L . grad (rL YLM)] ≈ (in prima grossolana approssimazione)
mc L  1
 1

e
r L 1YLM 
mc L  1

La classica stima di Weisskopf dell’elemento di matrice delle transizioni e.m.
Cosiddette stime di particella singola
La stima tradizionale dell’elemento di matrice e’ stata fatta da Weisskopf assumendo che la
transizione sia fatta da un solo nucleone, cioe’ si tratti di una sola particella, ci troviamo quindi in
una descrizione di modello a Shell estremo
Si assume inoltre che entrambe le funzioni d’onda radiali sia uguali, costanti sul nucleo e zero al di
fuori e cioe’:
 f (r )   i (r )  (cos t ) e ovviamente normalizzate ad 1.
L’integrale sulle tre armoniche sferiche che descrivono la dipendenza angolare delle due funzioni
d’onda e del operatore multipolare si approssima all’unita’ fermo rimanendo che deve esere
soddisfatta la regola triangolare: Ji = Jf + L
.Allora abbiamo, integrando fra 0 e R (raggio nucleare), dato che la funzione d’onda è = 0 al di
fuori del nucleo per ipotesi:
R
e (cos t )2 r L r 2 dr
R L 3 3
3R L
*
e
M(L) =   f m(L) i dV =
=
=
e
2 2
L  3 R3
( L  3)
0
 (cos t ) r dr
1
Bisogna inoltre aggiungere un termine 4 al denominatore che viene dalla normalizzazione della
parte angolare della funzione d’onda dello stato finale: f(r, = cost / 4
______________________________
Mettendo assieme le formule ricavate si ha alla fine:
2( L  1)
 


2 
  o L[( 2 L  1)!!]   c 
1
2 L 1
e2  3 


4  L  3 
2
1


 r0 A 3 




2L

2L
2 L 1
2
1

e 2  3  
c

  r0 A 3 
40  L  3  

Nel caso del dipolo elettrico abbiamo L=1 , la formula diventa con r0 = 1.2 fm:
2( L  1)
  
=


2
L[( 2 L  1)!!] c  c 
2
1


1.2 xA3  c = 10+14 E3 A2/3 sec -1.




e2
[Inserendo i valori numerici: c  197 MeVfm ,
= 1.44 MeV fm, c = 3 x 10+23 fm/sec.]
40
2(1  1)
1
e2  3 
2 L 1


E
 

1[( 2  1)!!]2
c 2 L2 40  4 
2
L ’ordine di grandezza dell’ operatore multipolo elettrico e’ circa: erL

er L = circa 1/10 erL
mentre per il multipolo magnetico:
mcR
B(E2) sp = 5.94 10-2 A4/3 e2fm4
P(E2)=1/ (sec-1) = 1.22 10+9 E(MeV) B(E2)e2fm4
Nucleo Ex(keV)
J 
Multipo. B(E2)W.u.
41
Ca7/21943
3/2- 0.44ps
E2
5.5
41
Sc 7/21716
3/2- 0.36ps
E2
12.7
17
17
F5/2+
O5/2+
495.33
870.73
1/2+ 286ps
1/2+ 179ps
E2
E2
25.0
2.39
Sviluppo di una distribuzione di carica in serie di multipoli
Il potenziale V(R) di una distribuzione di carica qualunque r) in un punto genrico P distante R
dall’origine con R >> r e’ dato da:
 (r )dV
 (r )dV
 (r )dV
4V(R) =  _ _  
=
=
2
2
2
R

r

2
rR
cos

r
r
| R r |
R 1  2 cos   2
R
R
il secondo e il terzo addendo sotto radice sono molto piccoli e quindi si puo’ sviluppare in serie;
consideriamo i termini fino al secondo ordine in r/R, e ricordando che lo sviluppo in serie di Taylor
e’ del tipo:
f(1+dx) = f(1) + f’(1)dx + f”(1)/ 2! dx2 + ......... si ottiene:
2

 1 3  r 2 2r

 (r )  1  r 2 2r
 2  cos    ......dV =
=
1   2  cos   
R  2 R
R
R
 2! 4  R



 (r )dV  (r )r cos dV  (r )r 2  3 2
1
=


 cos   dV  ....
2
3
R
2
R
R 2

 (r ) 
r
r2
=
P

P

P  ......dV con Pi polinomio di Legendre di ordine “i”.
 0
1
2 2
R 
R
R

Il primo addendo e’ il termine classico di potenziale di una carica tipo puntiforme, il secondo e’
quello di dipolo il terzo e’ quello di quadrupolo e cosi’ via.
In realta’ lo sviluppo vero e proprio in multipoli e’ piu’ complesso se si tiene in mente che il dipolo
e’in realta’ un vettore , quindi il quadrupolo e’ un ente piu’ complesso (cioe’ un tensore) e cosi’ via
per i termini di ordine superiore.
Alla fine nel caso di una sola carica e (per es. un protone):
m (L) = e rL YLm (

L
m
PL 0
YL,0
1
0
0
1
1
0
cos 
2
0
(3 cos2-1)/2
4
3
cos 
4
5
(3 cos 2   1)
16
ALCUNE FIGURE PER APPLICAZIONI, ESERCIZI