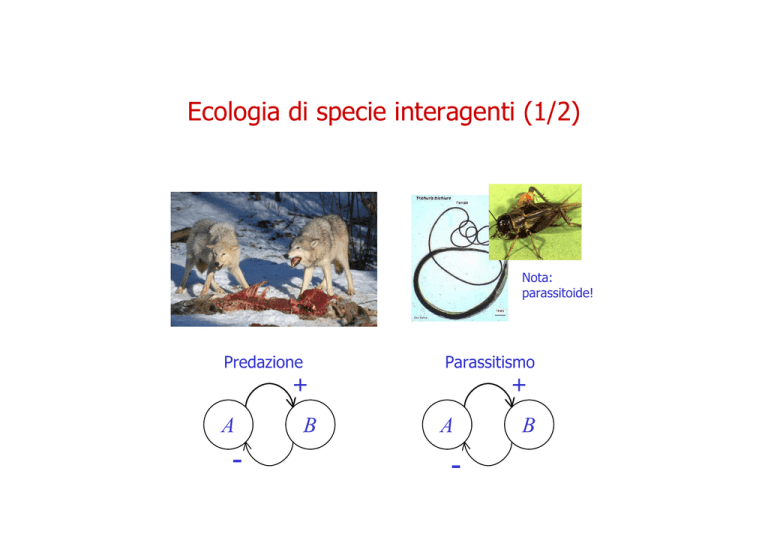
Ecologia di specie interagenti (1/2)
Nota:
parassitoide!
Predazione
+
A
-
B
Parassitismo
+
A
-
B
Ecologia di specie interagenti (2/2)
Competizione
Mutualismo
A
A
-
-
B
+
+
B
erbivoro
Diversificazione
dei consumatori
scavenger (spazzino)
carnivoro
La predazione:
reti trofiche e piramidi ecologiche
• Quali relazioni fra le popolazioni di un ecosistema
• Cos’è una rete trofica?
• Keystone species
• Approccio funzionalistico allo studio degli ecosistemi
• Piramidi ecologiche e bilanci energetici
Cos’è una rete trofica? E una catena?
•
Elton (1923): who eats whom?
• seppure la più semplice rimase
incompleta: osservazione +
contenuti stomacali o pellet
• convenzioni (frecce)
•
Reti trofiche in comunità tropicali ed esplosiva (i.e., esponenziale) difficoltà
•
Catene trofiche: livelli e ambiguità (secondo i cammini), lunghezza media
Esempio: Relazioni trofiche nella tundra a Barrow (Alaska)
Gufo delle nevi
Gufo dalle
orecchie corte
Cacciatore di
Pomerania
Gabbiano glauco
Cacciatore di
Pomerania parassita
Volpe artica
Volpe rossa
Donnola
minore
Cacciatore di
Pomerania dalla
coda lunga
Donnola dalla
coda corta
Lemming (specie
Lemmus e Dicrostonyx )
Vegetazione a tundra
Catene di pascolo e di detrito a Wytham Woods
Luce
Produttori
primari
Consumatori
primari
Lettiera
Alberi e
cespugli
Erbe
Falene
invernali
Insetti
Querce
Tortrix
Arvicole
e topi
Consumatori
secondari
Ragni
Consumatori
terziari
Parassiti
Cinciallegre
Gufi
Donnole
Cyzenis
Iperparassiti
Altri
defoliatori
Vermi
del suolo
Philonthus
Abax
Feronia
Topiragno
Funghi
Insetti
del suolo
Talpe
Interazioni forti, keystone species e rischi
• Si può semplificare la struttura tenendo conto dei soli legami forti
• Keystone species : cosa sono? (Paine, 1966)
Heliaster
(stella marina)
Muricanthus
(gasteropode)
Acanthina tuberculata
(gasteropode)
Hexaplex
(gasteropode)
Morula
(gasteropode)
Columbellidae
(gasteropodi)
5 specie
Bivalvi
13 specie
Cantharus
(gasteropode)
Gasteropodi erbivori
14 specie
Heliaster sp.
Acanthina angelica
(gasteropode)
Cirripedi
3 specie
Chitoni
2 specie
Brachiopodi
1 specie
Specie esogene e semplificazione di reti trofiche:
Il pesce persico nel lago Vittoria
Approccio funzionalistico
(1/3)
• Cosa sono gli organismi?
• Flussi di materia e di energia (differenze e difficoltà)
• Catene di pascolo e di detrito
R
R
CD2
C2
R
Schema
semplificato
dei flussi
energetici
R
C1
M
M
CD1
R
R
H
M
M
D
M
R
P
SOLE
M
M
MOM
Approccio funzionalistico
(2/3)
• Equazione di bilancio
• Da cui
dE
= Fin − Fout
dt
ì dP
ï dt = es Fs − µ P P − FH
ï
ï dH = e F − µ H − F
H H
H
C1
ï dt
í
ï dC1 = e F − µ C − F
C1 C1
C1 1
C2
ï dt
ï dC
ï 2 = eC 2 FC 2 − µC 2C2
ïî dt
• Significato dei parametri
• Relazioni di equilibrio e degradazione
(piramidi energetiche)
Approccio funzionalistico
Prateria
in estate
(3/3)
C2 = 1
C1=90000
H=200000
P = 1500000
Inverno
Estate
C1=6
H = 12
C1=3
H = 10
P = 100
P=2
C2 = 2
C1=120000
Piramidi di numeri
(individui in 0.1 ha)
H = 150000
P = 200
Foresta temperata
(Wytham Woods)
in estate
Piramidi di biomassa
(mg peso secco per m3 nel lago e
g peso secco per m2 in foresta)
C1=1
D=10 H=4
P = 40000
Foresta tropicale
(Panama)
Plancton nel lago Maggiore
Biomassa
C2=1.5
C1=11
D=5
H=37
P = 809
Piramidi di biomassa (kcal per m2)
e di flussi energetici entranti
nei diversi comparti (kcal per m2 per anno)
a Silver Spring (Florida)
D=5060
Flussi
C2=1
C1=383
H=3368
P = 20810
(1/3)
predator density
Vito Volterra (1928)
Approccio popolazionistico
prey density
Can we reproduce oscillations at least in
laboratory populations?
Approccio popolazionistico
“No mathematical theories
can be accepted by biologists
without a most careful
experimental verification ”
– Gause, 1934 (Chapter 4)
Paramecium
caudatum
Didinium
nasutum
(2/3)
Approccio popolazionistico
(3/3)
Eotetranychus
sexmaculatus
Typhlodromus
occidentalis
Modelli consumatori risorsa
• Ipotesi
• Forma generale
• Il modello di Lotka-Volterra
K
Il concetto di risposta funzionale
Holling 1959
Tre tipi di risposta funzionale
Il modello del chemostato (o dell’agricoltore!)
αx
ì dx
ï dt = φin − δx − y x + β
ï
í
ï dy = −µy + ey αx
ïî dt
x +β












