Esercitazioni di Economia Politica (Microeconomia) – [email protected]
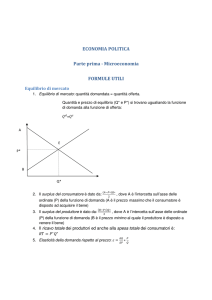
DOMANDA E OFFERTA
Introduzione
La funzione o curva di domanda esprime la quantità domandata di un certo bene in funzione del
suo prezzo ed è solitamente scritta nella seguente forma:
QD = 12 – 2P
Si è, infatti, interessati a come varia il comportamento del consumatore rappresentativo in risposta
ad una variazione del prezzo. La relazione negativa è assolutamente intuitiva: all’aumentare del
prezzo, il consumatore domanderà una quantità minore del bene perché è diventato relativamente
più povero (effetto reddito) o perché sceglierà altri beni meno costosi (effetto sostituzione). In
particolare, il coefficiente associato al prezzo, – 2, rappresenta la pendenza, cioè la variazione della
quantità domandata al variare del prezzo. Il valore 12 è invece l’intercetta verticale (detta anche
costante perché non dipende da P), cioè il valore di QD che si raggiunge quando P = 0.
(IMPORTANTE): dal momento che si parlerà sempre di rette (cioè di funzioni aventi pendenza
costante), quando ci si trova di fronte ad una equazione (sia di domanda che di offerta), il modo
più semplice per calcolare la pendenza è ricordarsi questa semplice regola:
Pendenza = ∆QD / ∆P = variazione di QD al variare di P = coefficiente associato alla variabile
indipendente.
Nel caso analizzato, è appunto pari a – 2.
Se l’equazione fosse QD = 12 – P la pendenza sarebbe – 1 e non zero!
È possibile, tuttavia, esprimere la funzione o curva di domanda nella sua forma “inversa”, vale a
dire esprimere il prezzo in funzione della quantità domandata attraverso semplicissimi passaggi
algebrici:
QD = 12 – 2P
2P = 12 – QD
P = 6 – 0,5QD.
Come si vedrà in seguito sono utili entrambe le rappresentazioni; anzi, in alcuni casi è preferibile
usare la prima (come nel calcolo dell’elasticità), mentre in altri casi è preferibile usare la forma
“inversa” (determinazione del surplus del consumatore). Sono, quindi, due opzioni che a seconda
dei casi consentono di risolvere in maniera più intuitiva gli esercizi (combinando ragionamento
economico e procedimento matematico).
Ovviamente se siamo interessati a come varia P al variare di Q, dobbiamo tener conto della
funzione nella sua forma “inversa” e ripetere la regola già vista prima:
P = 6 – 0,5QD
Pendenza = ∆P / ∆QD = variazione di P al variare di QD = – 0,5
Equazione e grafico
Nel costruire il grafico dell’equazione occorre fare attenzione alla forma scelta/usata della funzione.
Infatti, utilizzando la funzione di domanda “diretta” QD = 12 – 2P, 12 è l’intercetta verticale, 12/2 =
6 è l’intercetta orizzontale (il valore di P quando QD = 0) e – 2 è la pendenza.
Se la forma usata, invece, è quella “inversa”, cioè P = 6 – 0,5QD, allora 6 è l’intercetta verticale, 12
è l’intercetta e – 0,5 è la pendenza.
1
Esercitazioni di Economia Politica (Microeconomia) – [email protected]
La funzione o curva di offerta esprime la quantità offerta di un certo bene in funzione del prezzo
ed è solitamente scritta nella forma:
P = 2 + QO
Ciò per via della stretta relazione che lega prezzo, costo (marginale) e quantità offerta. Un aumento
della quantità offerta implica un incremento del costo variabile (quello legato alla produzione del
bene); di conseguenza, l’impresa aumenterà il prezzo al fine di “coprire” l’incremento del costo
variabile (cioè il costo marginale).
La relazione può anche essere vista sotto un altro punto di vista: all’aumentare del prezzo, il
venditore sarà invogliato a offrire una quantità maggiore del bene:
QO = P – 2
Come nel caso della domanda, le due forme della funzione di offerta rappresentano utili opzioni da
usare a seconda dei casi per risolvere più facilmente gli esercizi.
La regola introdotta in precedenza vale anche per la curva di offerta:
Pendenza = ∆P / ∆QO = variazione di P al variare di QO = + 1
Discorsi analoghi a quelli fatti per la costruzione del grafico della curva di domanda valgono per la
curva di offerta. Nel caso della curva di offerta espressa nella forma QO = P – 2 si faccia solo
attenzione all’intercetta verticale che è negativa.1
Esercizi
1) Si scriva l’equazione della retta rappresentata nella figura in basso (in entrambe le forme).
P
12
A
8
4
B
2
4
6
Q
È immediato notare che si tratta di una funzione di domanda: la retta, infatti, rappresenta una
relazione negativa tra prezzo e quantità. Inoltre, l’intercetta verticale (il valore di P quando Q = 0)
è pari a 12, mentre quella orizzontale (il valore di Q quando P = 0) è pari a 6.
Per calcolare la pendenza è necessario scegliere due punti (abbiamo bisogno della variazione di P
e Q) qualsiasi poiché la pendenza non cambia. Passando dal punto A al punto B, ad esempio, la
distanza verticale è pari alla variazione/riduzione del prezzo ∆P = (4 – 8) = – 4, mentre quella
orizzontale è pari alla variazione/incremento della quantità domandata ∆QD = (4 – 2) = 2.
Di conseguenza, la pendenza della funzione inversa di domanda ∆P / ∆QD = – 4/2 = – 2, mentre il
suo reciproco – 0,5 è la pendenza della funzione diretta, infatti ∆QD / ∆P = 2 / – 4 = – 0,5:
P = 12 – 2Q
Q = 6 – 0,5P
1
In realtà, la funzione di offerta andrebbe espressa come P = β·QO, dove è la pendenza. In questo caso quando P = 0
anche QO = 0 e viceversa.
2
Esercitazioni di Economia Politica (Microeconomia) – [email protected]
Un modo forse più semplice e intuitivo di ricavare la pendenza è costruire una tabella con i valori
riportati nel grafico:
Prezz
o
Quantit
à
12
0
8
2
4
4
0
6
È immediato notare che quando il prezzo scende (sale) di 4 punti, la quantità domandata sale
(scende) di due unità. Quindi, la variazione di P al variare di un’unità di Q D è pari a – 2 e la
variazione di QD al variare di un’unità di P è – 0,5.
2) Sia P = 2 + 2QO la funzione di offerta e QD = 11 – P quella di domanda (diretta). Si ricavi
prezzo e quantità di equilibrio.
La condizione di equilibrio è QD = QO = Q (domanda e offerta sono eguagliate dal prezzo finale di
vendita che “soddisfa” venditore e compratore). Di conseguenza, riscrivendo la funzione di offerta
come QO = 0,5P – 1, si ricava che:
0,5P – 1 = 11 – P, cioè 1,5P = 12 da cui P = 12/1,5 = 8 e Q = 3
Tuttavia, nello specifico è forse più semplice eguagliare i prezzi, poiché è semplicissimo ricavare la
curva di domanda inversa che è P = 11 – QD. Il risultato finale ovviamente non cambia:
2 + 2Q = 11 – Q, quindi 3Q = 9 da cui si ricava Q = 9/3 = 3.
3