misure di resistenza con il metodo di confronto

MISURE DI RESISTENZA
CON IL METODO DI CONFRONTO DELLE CADUTE DI TENSIONE
1. Premessa
Oggigiorno esistono strumenti compatti e semplici da utilizzare per la misura di resistenza: gli ohmetri
(parte integrante dei multimetri). Tali strumenti mostrano però evidenti limiti quando si intendono
-2
-6
misurare con elevata precisione resistenze di piccolo valore (pochi ohm o frazioni: 10 ÷ 10 Ω) quali
avvolgimenti di macchine elettriche, spezzoni di cavi o conduttori di linee, shunt, di barre di rame, ecc.,
per la misura della resistività attraverso la misura della resistenza di un campione filiforme. In questi
casi è necessario ricorrere a “metodi” alternativi agli strumenti quali:
• Metodi a caduta di tensione
• Ponte di Thompson.
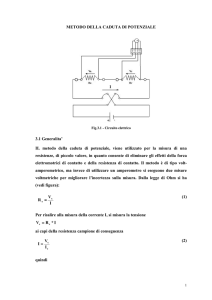
La resistenza di un resistore in c.c. è definita, per la legge di Ohm, come il rapporto tra la tensione ai
morsetti e la corrente di circolazione (fig. 1):
E
I metodi di misura che si basano sulla applicazione della definizione della legge di Ohm si chiamano
Metodi a caduta di tensione ed esistono diversi metodi a seconda degli schemi e degli strumenti che si
adoperano. Il più semplice prevede l’impiego di un voltmetro e di un amperometro ed è noto come
Metodo voltamperometrico, in fig. 2 è riportato uno dei possibili schemi.
E
E
Il metodo sembra semplice: in realtà i due strumenti (a causa delle loro resistenze interne:
“piccola” ma non nulla per l’amperometro, “grande” ma non infinita per il voltmetro), una
volta inseriti nel circuito, provocano variazioni delle grandezze elettriche (corrente e tensione)
rispetto
a
quelle
che
si
avrebbero
in
assenza
degli
strumenti
(fig.
3).
È impossibile misurare la corrente e la tensione che interessano la resistenza R senza
prescindere da tali variazioni.
Osserviamo che:
• Con una opportuna scelta degli strumenti le variazioni di corrente e di tensione possono essere
trascurabili
• Le variazioni di corrente e di tensione possono essere determinate e portate in conto.
2. Metodo di confronto delle cadute di tensione
Con detto metodo le “perturbazioni” causate dagli strumenti di misura, nella maggior parte dei casi
pratici, hanno minore influenza sulla misura: il metodo prevede che la stessa corrente attraversi sia la
resistenza oggetto della prova, sia una resistenza campione, con un voltmetro si confrontano le due
rispettive cadute di tensione.
E
Fig. 4 metodo di confronto delle cadute di tensione (schema di principio)
Un terzo metodo (Metodo potenziometrico) è analogo al precedente: si sostituisce al voltmetro un
potenziometro rendendo nulle le perturbazioni ed ottenendo anche maggior precisione (con costi
superiori).
3. Difficoltà nella misura di piccole resistenze
Supponiamo di voler misurare la resistenza R definita tra le estremità A e B dei morsetti accessibili M
(fig. 5):
Il valore di R può essere determinato dal rapporto tra la CdT che si stabilisce tra A e B e la
relativa corrente di circolazione.
In pratica, quando si deve realizzare l’inserzione di R nel circuito di misura, sono possibili i due schemi
di montaggio indicati in fig.6 e fig.7 (si è fatta per semplicità l’ipotesi di porre i
puntali del voltmetro in posizioni simmetriche):
dove:
-c sono i cavetti di adduzione della corrente
-rc sono le resistenze di contatto localizzate nei punti in cui i morsetti A e B si innestano ai cavetti c
-r1, ed r'1, sono, rispettivamente, le resistenze di una parte dei morsetti M e di un tratto dei cavetti c.
A prescindere dal consumo dello strumento volumetrico (corrente derivata nel voltmetro), si osserva
che la misura della resistenza, intesa come rapporto tra le tensione letta al voltmetro e la corrente
inviata, è affetta da un “errore sistematico”.
Infatti, nei casi riportati in fig. 6 e 7, detto Rm il valore della misura, risulta rispettivamente:
La differenza tra valore misurato Rm ed il valore effettivo della R è funzione (a seconda dei casi) delle
resistenze rc, r1, ed r'1,. Infatti: r1 ed r'1 dipendono dalla lunghezza e sezione dei rispettivi tratti; le
resistenze di contatto rc dipendono dallo stato delle superfici, dalla pressione dei contatti, dalla natura
dei materiali, ecc. ed hanno valori variabili; anche in collegamenti accurati le rc possono assumere
-4
valori dell'ordine di 10 Ω.
Di conseguenza, se la misura riguarda resistenze dell'ordine della decina di ohm o maggiore l’errore
sistematico rappresentato da 2*r1 o da 2*(rc+r’1) non ha influenza sulla precisione propria del
-1
-2
metodo di misura adottato, se invece la resistenza da misurare ha valori dell’ordine di 10 ÷ 10 Ω o
inferiore, l'errore dovuto alle sole resistenze di contatto, nel caso si voglia misurare un centesimo di
ohm, potrebbe assumere valori anche di qualche percento. Questa conclusione mette in luce una delle
difficoltà che presenta la misura di precisione di piccole resistenze. Diviene perciò indispensabile
ricorrere ad accorgimenti particolari.
4. Resistori a 4 morsetti
Uno di questi accorgimenti consiste nel munire la resistenza oggetto della misura di 4 morsetti
accessibili come indicato in fig. 8:
E
I morsetti più esterni servono per addurre la corrente e sono detti morsetti amperometrici;
l morsetti più interni servono per rilevare la tensione e sono detti morsetti voltmetrici.
Il valore di resistenza che in tal caso si misura è quella definita tra i punti di attacco dei
morsetti interni:
R = V/I.
Questo valore non include le resistenze di contatto ra presenti in corrispondenza dei morsetti
amperometrici.
D'altra parte il circuito collegato ai morsetti voltmetrici ha di solito resistenza elevata rispetto
ad R ed è attraversato da correnti molto piccole; quindi le CdT sulle resistenze di contatto rv,
sono trascurabili rispetto a V, e non causano errore apprezzabile nella determinazione di R.
Riepilogando:
Il valore della resistenza a 4 morsetti definito come rapporto tra la CdT misurata ai morsetti
voltmetrici e la corrente di circolazione non è praticamente affetto da errore sistematico dovuto alle
resistenze di contatto.
5. Misura di resistenza con il metodo di confronto delle cadute di tensione
Il metodo di confronto delle cadute di tensione, che deriva dal metodo voltamperometrico, ben si presta
per la rapida misura di piccole resistenze (quali di spezzoni di cavo elettrico, di avvolgimenti di
macchine elettriche, ecc.) quando non si dispone contemporaneamente (come nel metodo
voltamperometrico) di un voltmetro e di amperometro di adeguate portate ed accuratezze, e si dispone
invece di un solo millivoltmetro e di resistori di precisione e quattro morsetti.
E
fig. 9 - Schema del circuito di misura
Con riferimento al circuito in figura, quando il millivoltmetro è commutato su Rc, la caduta di tensione
Vc misurata dallo strumento ai morsetti voltmetrici di Rc vale:
Quando il millivoltmetro è commutato su Rx, la caduta di tensione Vx misurata dallo strumento ai
morsetti voltmetrici di Rx vale:
Dove Rv indica la resistenza interna del millivoltmetro ed Rs rappresenta la somma di tutte le altre
resistenze presenti nella maglia di alimentazione (eventuale reostato di regolazione della corrente, cavi
di collegamento, resistenza interna della batteria o dell’alimentatore stabilizzato). Dividendo membro a
membro le precedenti espressioni si ottiene:
Dividendo numeratore e denominatore per Rv si ottiene
E considerato che solitamente Rv >> Rx :
risulta, nel caso peggiore:
NB:
Nell’ipotesi che sia verificata la (5), alla determinazione della Rx e della sua incertezza ( (6) e (7) ),
non danno contributo:
• il valore di Rs, b
• l’indicazione dell’amperometro,
quindi:
• non è indispensabile che la Rs sia nota con precisione, è invece indispensabile che non vari durante la
misura ad esempio a causa di riscaldamento per effetto Joule,
• non è indispensabile che l’amperometro sia uno strumento particolarmente preciso: la sua funzione è
solo quella di “monitorare” la corrente di circolazione.
6. Esempio numerico
Si vuole misurare la piccola resistenza Rx di una barra di rame a quattro morsetti, avente le
caratteristiche riportate nella tabella 1, con il metodo di confronto delle cadute di tensione disponendo
un millivoltmetro digitale in corrente continua (Multimetro HP 34401 A) con le caratteristiche riportate
nella tabella 2. È richiesta una incertezza di 1 %
Tab.1
Componente in prova: barra di rame con le seguenti caratteristiche:
1,76 *10-8 Ω m
resistività a 20 °C (ρ)
lunghezza (l)
0,9 m
sezione (s)
(3 * 30) mm2
0,0042 K-1
coefficiente medio di temperatura tra 0 e 100 °C (α)
Resistenza Rx stimata
0,176 mΩ
Tab. 2
Voltmetro (multimetro HP 34401 A)
Portata
100 mV
risoluzione
100 nV
resistenza di ingresso
> 10 GΩ
incertezza di misura UV
± (0,0050 % della lettura + 0,0035 % della portata)
Con riferimento al circuito di figura ed utilizzando:
• una resistenza campione a quattro morsetti Rc = 0,10000 mΩ nota con una incertezza pari allo 0,01
%, corrente massima sopportabile Imax=10A;
• un alimentatore stabilizzato HP 3631 A (avente ripple, rumore e resistenza interna trascurabili) che
può fornite una tensione variabile massima pari a E ≅ 6 V che consente la circolazione di una corrente
di lavoro massima di I ≅ 5 A
Determiniamo la massima corrente che può circolare:
In condizioni di regime termico:
2
Rx · I = k · S ·∆T
dove:
(8)
2
•
k = 10 W /(m K) è il fattore di adduzione del calore che porta in conto fenomeni di convezione
ed irraggiamento (il valore assegnato è desumibile da tabelle riportate sul Manuale dell’ingegnere;
•
S è la superficie attraverso cui avviene la trasmissione del calore (che coincide con la superficie
2
laterale del conduttore rigido assegnato) e vale S = 0,059 mm . Essendo l’incertezza richiesta pari a 1
%, la variazione di resistenza a causa dell’autoriscaldamento della barra deve essere contenuta entro
0,05%; quindi, essendo:
R(T2 ) = R(T1) ·(1+α·∆T)
(9)
l’errore dovuto al riscaldamento del conduttore vale:
quindi il valore massimo della corrente che può circolare vale:
Tab. 3
Il nostro alimentatore stabilizzato è in grado di fornire 5 A e risulta quindi idoneo per l’alimentazione
del circuito di misura.
Essendo la somma delle resistenze Rx, Rc e dei collegamenti pari circa a R = 0,3 mΩ è necessario
applicare (per consentire la circolazione di una corrente inferiore a 20 A ed anche inferiore a 5 A) una
f.e.m.:
-3
E = R*I = 0,3 *10 *5 =1,5 mV.
Non avendo l’alimentatore stabilizzato disponibile in laboratorio una adeguata sensibilità di
regolazione, siamo costretti a inserire un reostato (ad esempio da 5Ω, Imax =10A) impostato su 1 Ω
allo scopo di ottenere 5 A con una tensione di alimentazione di 5 V.
Si eseguono quindi le seguenti misure di caduta di tensione:
Vx = 0,7948 mV;
Vc = 0,4524 mV
(12)
La misura è effettuata nelle seguenti condizioni ambientali: temperatura: 20,5 °C; umidità relativa: 60
%; aria ferma.
Con riferimento alla tabella 3 che riporta le specifiche in c.c. del voltmetro non occorre
effettuare correzioni dovute alla temperatura ambiente.
Considerato che risulta verificata la relazione (5) :
risulta:
e quindi sostituendo i valori numerici:
(la precedente relazione è scritta in modo non corretto con tutte le cifre fornite dalla calcolatrice)
Per quanto riguarda le incertezze di misura, essendo:
possiamo quindi scrivere:
In definitiva:
Rx = (175,7 ± 2,1) µΩ = 175,7 µΩ ± 1,2 %
N.B.1: Valutazione dell’incertezza, tenendo presente che si è usato un voltmetro digitale (con
incertezza espressa in formula binomia), adoperandolo sulla medesima portata.
Come si ricorda dalla teoria, un voltmetro digitale con dichiarazione d’incertezza in formula binomia
utilizzato sulla portata VFS presenta nella misura di una tensione V, un errore assoluto complessivo
somma di un errore di lettura (che porta in conto l’errore di guadagno) proporzionale alla lettura, e di
un errore di portata in generale indipendente dalla lettura (che porta in conto errore di offset, di non
linearità integrale e di quantizzazione). Tale errore assoluto e la sua versione relativa sono
rispettivamente espressi dalle seguenti relazione:
EV = ELV + EPV = EG ⋅ V + EPV
eV =
EV ELV + EPV
E
=
= EG + PV = eLV + ePV
V
V
V
Risulta quindi che l’errore relativo di lettura non dipende dalla lettura V, risultando quindi costante su
tutta la scala e pari all’errore di guadagno: questo significa che tutte le letture che vengono effettuate
sulla stessa scala presentano il medesimo errore relativo di lettura, maggiorato dal costruttore con
l’incertezza relativa (%) di lettura, che ritroviamo nella dichiarazione dell’incertezza:
incertezza di
misura UV
± (0,0050 % della lettura + 0,0035 % della portata)
Di contro, l’errore relativo di portata ePV = EPV V dipende non solo dalla lettura a denominatore del
rapporto, ma anche dal numeratore, che come è stato già precisato, porta in conto gli errori di offset, di
non linearità integrale e di quantizzazione, dei quali gli ultimi due dipendono anch’essi dalla particolare
lettura. Di conseguenza l’errore relativo di portata non è costante né in modulo, né in segno.
Veniamo ora alla misura del rapporto Vx/Vc, il cui errore relativo, come è noto, è espresso da:
eVx Vc =
EVx
Vx
−
EVc
Vc
=
ELVx
Vx
+
EPVx
Vx
−
ELVc
Vc
−
EPVc
Vc
= eLV +
EPVx
Vx
− eLV −
EPVc
Vc
=
EPVx
Vx
−
EPVc
Vc
Questo significa che la maggiorazione del suo modulo (incertezza relativa) è pari a:
eVx Vc =
EPVx
Vx
−
EPVc
Vc
≤
EPVx
Vx
+
EPVc
Vc
≤
⎛ 1
U PV U PV
1 ⎞
+
= U PV ⎜⎜
+
⎟⎟ = uVx Vc
Vx
Vc
⎝ Vx Vc ⎠
e pertanto le formule da adoperare nella misura della resistenza col metodo di confronto a CdT, con
sensibile riduzione nella valutazione dell’incertezza rispetto al caso precedente, risultano:
⎡
⎛ 1
1
+
U Rx = Rx ,m ⎢U PV ⎜
⎜ Vx ,m Vc ,m
⎢⎣
⎝
U Rx , std = Rx ,m U
2
PV , std
⎞ UR
c
⎟+
⎟ Rc ,m
⎠
⎤
⎥
⎥⎦
2
⎛ 1
1 ⎞ U Rc , std
⎜⎜ 2 + 2 ⎟⎟ + 2
⎝ Vx ,m Vc ,m ⎠ Rc , m
Naturalmente, UPV risulta dalla tabella di cui sopra, come incertezza assoluta di portata:
incertezza di
misura UV
± (0,0050 % della lettura + 0,0035 % della portata)
N.B.2: Valutazione dell’incertezza, tenendo presente che si è usato un voltmetro digitale (con
incertezza espressa in formula polinomia), adoperandolo sulla medesima portata.
Come si ricorda dalla teoria, un voltmetro digitale con dichiarazione d’incertezza in formula polinomia
utilizzato sulla portata VFS presenta nella misura di una tensione V, un errore assoluto complessivo
somma di un errore di lettura (che porta in conto l’errore di guadagno) proporzionale alla lettura,
nonché dei seguenti errori: un errore di offset indipendente dalla lettura, un errore di non linearità
integrale dipendente dalla lettura, ed un errore di quantizzazione, anch’esso dipendente dalla lettura.
Tale errore assoluto e la sua versione relativa sono rispettivamente espressi dalle seguenti relazioni:
EV = EG ⋅ V + Eo + Einl (V ) + Eq (V )
eV =
EV EG ⋅ V + Eo + Einl (V ) + Eq (V )
E E (V ) Eq (V )
=
= EG + o + inl
+
V
V
V
V
V
Risulta quindi che l’errore relativo dovuto al guadagno non dipende dalla lettura V, risultando quindi
costante su tutta la scala: questo significa anche qui che tutte le letture che vengono effettuate sulla
stessa scala presentano il medesimo errore relativo dovuto al guadagno (errore relativo di lettura).
Di contro, gli altri tre errori relativi dipendono dalla lettura: in particolare, l’errore relativo di offset
eo = Eo V dipende dalla lettura a denominatore del rapporto (ma il numeratore è costante su tutta la
scala), l’errore relativo di non linearità integrale einl = Einl (V ) V e l’errore relativo di quantizzazione
eq = Eq (V ) V dipendono non solo dalla lettura a denominatore del rapporto, ma anche dal numeratore,
variabile a seconda della particolare lettura. Di conseguenza, questi ultimi due errori relativi non sono
costanti né in modulo, né in segno, mentre il primo dei tre ( eo = Eo V ), essendo costante il suo
numeratore, cambia solo in modulo al variare della lettura, ma non nel segno.
Veniamo quindi alla misura del rapporto Vx/Vc, il cui errore relativo è ora espresso da:
eVx Vc =
EVx
Vx
−
EVc
Vc
= EG +
Eo Einl (Vx ) Eq (Vx )
E E (V ) E (V )
+
+
− EG − o − inl c − q c =
Vx
Vx
Vx
Vc
Vc
Vc
⎛ 1 1 ⎞ E (V ) E (V ) E (V ) E (V )
= Eo ⎜ − ⎟ + inl x − inl c + q x − q c
Vx
Vc
Vx
Vc
⎝ Vx Vx ⎠
Questo significa che la maggiorazione del suo modulo (incertezza relativa) è pari a:
⎛ 1 1 ⎞ E (V ) E (V ) Eq (Vx ) Eq (Vc )
1 1
1
eVx Vc = Eo ⎜ − ⎟ + inl x − inl c +
−
≤ Eo
−
+ Einl (Vx )
+
Vx
Vc
Vx
Vc
Vx Vx
Vx
⎝ Vx Vx ⎠
+ Einl (Vc )
⎛ 1
1
1
1
1 1
1 ⎞
+ Eq (Vx )
+ Eq (Vc )
≤ Uo
−
+ (U inl + U q ) ⎜⎜
+
⎟⎟ = uVx Vc
Vc
Vx
Vc
Vx Vx
⎝ Vx Vc ⎠
e pertanto le formule da adoperare nella misura di resistenza col metodo di confronto a CdT, con
notevole riduzione nella valutazione dell’incertezza, risultano:
⎡
⎛ 1
1
1
1
U Rx = Rx ,m ⎢UV ,o
−
+ (UV ,inl + UV , q ) ⎜
+
⎜ Vx , m Vc , m
Vx ,m Vc , m
⎢⎣
⎝
2
U Rx , std = Rx ,m U
2
V , o , std
⎞ UR
c
⎟+
⎟ Rc ,m
⎠
⎤
⎥
⎥⎦
2
⎛ 1
⎛ 1
1 ⎞
1 ⎞ U Rc , std
2
2
−
⎜⎜
⎟⎟ + (UV ,inl , std + UV , q , std ) ⎜⎜ 2 + 2 ⎟⎟ + 2
⎝ Vx ,m Vc , m ⎠
⎝ Vx ,m Vc , m ⎠ Rc , m
MISURA DELLA RESISTENZA DI UNO SPEZZONE DI CAVO IN RAME
ATTRAVERSO IL METODO DI CONFRONTO A CADUTA DI TENSIONE
ρl
, dove ρ è la resistività
s
(espressa usualmente in Ω⋅m), l è la lunghezza, s = π D 2 4 (con D diametro) è la sezione del
conduttore.
Per un conduttore filiforme, come è noto, la resistenza è espressa da: Rx =
Sia dato quindi un conduttore di rame in guaina isolante (di diametro
esterno D’), per il quale si assuma ρ ≈ 2 ⋅10−8 Ω⋅m a 20 °C, il coefficiente
medio di temperatura α = 0,0042 K-1, un fattore di adduzione del calore
medio rame+guaina (che porta in conto fenomeni di convezione ed
irraggiamento) pari ancora a k = 10 W /(m2K) circa.
D’
D
Per ottenere un valore di massima della resistenza da misurare, si misura
con il calibro il diametro D del filo in rame, e con un metro estensibile la
lunghezza l compresa tra le due pinze voltmetriche (centro-centro),
adoperando la formula teorica sopra citata.
Si sceglie a questo punto la resistenza campione Rc a quattro morsetti da
collegare in serie alla Rx, prendendo quella di valore ad essa più vicino (ve
ne sono due: una da 0,01 Ω e l’altra da 0,001 Ω, con incertezza U Rc .
A
V
l
Per determinare la corrente massima da far scorrere nel provino, si adotta la
formula già vista nell’esempio numerico, a proposito del calore trasmesso
all’esterno:
4ρl 2
I
2
4ρ I 2
Rx · I 2 = k · Sl ·∆T, da cui: ∆T = π D
= 2
k (π D′l ) kπ D′D 2
V
A
Ipotizzando un errore relativo di temperatura inferiore allo 0,05%, si ottiene, come si è visto:
∆T =
4ρ I 2
≤ 0,12 K , da cui si ricava il valore massimo Imax della corrente di alimentazione.
kπ 2 D′D 2
Scelta una corrente I0 adeguatamente inferiore a Imax, si imposta il generatore in c.c. in modo tale da
fornire una corrente costante pari ad I0.
Si alimenta la resistenza in prova in serie con quella campione Rc (connessa con i suoi morsetti
amperometrici, riconoscibili in quanto più spessi), attraverso il generatore, facendo circolare la corrente
I0. Si connette poi successivamente il voltmetro digitale (multimetro da banco con Rv molto elevata, il
cui valore va ricercato nelle sue specifiche) alle pinze voltmetriche del cavo in prova, rilevando la
misura di tensione Vx corrispondente. Poi si connette lo stesso voltmetro ai morsetti voltmetrici della
resistenza campione, registrando anche qui la misura di tensione Vc corrispondente.
Dopo aver verificato che l’errore di consumo risulta trascurabile, si ricava la misura di Rx attraverso la
nota formula:
V
Rx = x Rc
Vc
La misura va ovviamente scritta in base al congruo numero di cifre significative, in base all’incertezza
assoluta, valutata nel caso peggiore tenendo presente che la misura del rapporto tra le due tensioni è
stata effettuata adoperando lo stesso voltmetro (con formula d’incertezza binomia) sulla stessa portata:
⎡
⎛ 1
1
U Rx = Rx ,m ⎢U PV ⎜
+
⎜
⎢⎣
⎝ Vx , m Vc , m
⎞ UR
c
⎟+
⎟ Rc ,m
⎠
⎤
⎥
⎥⎦
Se invece si è cambiata la portata, la formula diventa ovviamente:
⎛ UV
UV
U Rc
U Rx = Rx , m ⎜ x + c +
⎜ Vx ,m Vc , m
Rc ,m
⎝
⎞
⎟
⎟
⎠
A questo punto si può verificare se il valore approssimativo stimato in partenza per Rx risulta
all’interno dell’intervallo di confidenza al 100 % così determinato.