Disuguaglianze tra gli elementi di un triangolo

Per la prima classe del Liceo
Disuguaglianze tra gli elementi di un triangolo
Problema1
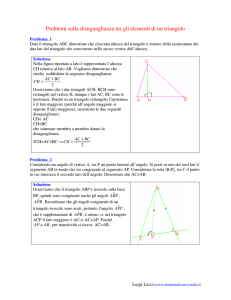
Considerato l’angolo r As di vertice A, non nullo, nè piatto, sia P un suo punto interno. Fissato sul lato r un
punto A in modo che risulti ABAP, si congiunga B con P e si prolunghi il segmento BP dalla parte di P fino
ad incontrare in C il lato s dell’angolo. Dimostrare che AC > AB.
Problema2
Dimostrare che in un triangolo qualsiasi l’altezza relativa ad un lato è minore della semisomma degli altri
due lati che concorrono nello stesso vertice da cui parte l’altezza suddetta.
Problema3
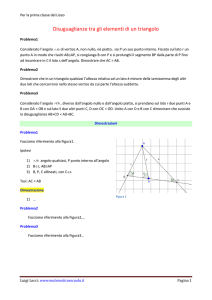
Considerato l’angolo rOs , diverso dall’angolo nullo e dall’angolo piatto, si prendano sul lato r due punti A e
B con OA < OB e sul lato S due altri punti C, D con OC < OD. Unito A con D e B con C dimostrare che sussiste
la disuguaglianza AB+CD < AD+BC.
Dimostrazioni
Problema1
Facciamo riferimento alla Figura1.
Ipotesi
1) r As angolo qualsiasi, P punto interno all’angolo
2) Br, ABAP
3) B, P, C allineati, con Cs
Tesi: AC > AB
Dimostrazione
1) Osserviamo che il triangolo ABP è isoscele su BP,
Figura 1
quindi i due angoli alla base ABP , APB sono congruenti (e acuti).
2) L’angolo APB è esterno rispetto al triangolo APC, quindi per il primo teorema dell’angolo esterno,
essendo maggiore di ciascuno degli angoli interni ad esso non adiacenti sarà APB  ACP . Dalla
congruenza ABP  APB deduciamo che ABP  ACP .
3) Nel triangolo ABC i due angoli nei vertici B, C sono disuguali, essendo ABC  ACB , poiché in un
triangolo all’angolo maggiore si oppone il lato maggiore, deduciamo che AC > AB. (C.V.D.)
Problema2
Facciamo riferimento alla Figura2, nella quale AH è l’altezza del triangolo relativa al lato BC.
Ipotesi
1)
ABC triangolo qualsiasi
Luigi Lecci: www.matematicaescuola.it
Pagina 1
Per la prima classe del Liceo
2) AH altezza relativa al lato BC
AH 
Tesi
1
 AB  AC 
2
Dimostrazione
Ricordato che “in un triangolo rettangolo l’ipotenusa è il
lato maggiore”, per i due triangoli AHB, AHC sussistono le
due disuguaglianze:
AH < AB,
AH<AC,
che sommate membro a membro forniscono la
disuguaglianza 2AH < AB+AC, equivalente alla seguente
AH<(AB+AC)/2, che rappresenta la tesi. (C.V.D.)
Figura 2
Problema3
Facciamo riferimento alla Figura3
Ipotesi
1) rOs angolo qualunque non nullo, né piatto.
2) A e B punti sul lato Or, con OA < OB
3) C e D punti sul lato Os, con OC <OD
Tesi:
AB + CD < AD + BC
Dimostrazione
Premessa - Ricordiamo che in ogni triangolo un lato è
minore della somma degli altri due.
Figura 3
1) Considerando il triangolo OBC sussiste la disuguaglianza OB < OC + BC.
2) Dal triangolo OAD ricaviamo la disuguaglianza OD < OA + AD.
3) Sommando membro a membro le due disuguaglianze otteniamo
OB+OD < OC+BC+OA+AD.
(*)
Osserviamo ora che per come sono stati scelti i punti A, B, C, D sui lati dell’angolo sussistono le
uguaglianze OB=OA+AB, OD=OC+CD, per cui la disuguaglianza (*) può assume la seguente forma
OA+AB+OC+CD < OC+BC+OA+AD
(*)
e sopprimendo nei due membri i segmenti OC, OA otteniamo
AB + CD < BC + AD
che rappresenta la tesi.
(C.V.D.)
Luigi Lecci: www.matematicaescuola.it
Pagina 2