Il calcolo combinatorio

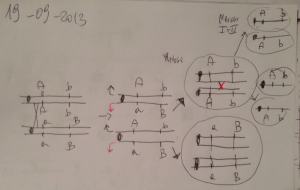
Il calcolo combinatorio
Il fattoriale di un numero
• Si indica con N! e si legge “N fattoriale”
• Indica il prodotto tra tutti i numeri naturali
minori e uguali (escluso lo zero) al fattoriale
del numero indicato
7!= 1●2●3●4●5●6●7
Calcolo combinatorio
• Se il cellulare di Luca ha una password di
accesso di 4 numeri, quanti sono le possibili
password?
Questo è un esempio di testo di un problema
risolvibile attraverso il calcolo combinatorio
Calcolo combinatorio
• Il calcolo combinatorio studia i
raggruppamenti che possono ottenere
ordinando un determinato numero di oggetti
disposizioni
permutazioni
combinazioni
Disposizioni semplici
• il numero degli oggetti è diverso dal numero
dei posti nei quali disporli
• Conta l’ordine della disposizione
D
n!
=
n,k
(n-k)!
___________________________________
Problema:
• Una persona possiede 4 quadri, ma lungo una
parete ne può appendere solo 3. ha importanza
anche l’ordine per questioni di interazioni lucecolore. In quanti modi può appenderli?
Permutazioni semplici
• Il numero degli oggetti è pari al numero dei
posti nei quali inserirli
• Conta l’ordine della disposizione
Pn
= n!
Problema:
• Un bambino gioca sulla spiaggia con 5 biglie di
diverso colore. In quanti modi le può mettere
in fila?
Combinazioni semplici
• Il numero degli oggetti è diverso dal numero
dei posti nei quali inserirli
• Non conta l’ordine della disposizione
C
n!
=
n,k k!(n-k)!
___________________________________
Problema:
• Consideriamo 5 punti nello spazio non
allineati. Quanti triangoli possiamo costruire?
B
E
A
D
C
Le ripetizioni
• Se in un raggruppamento un elemento può
comparire più volte, allora i gruppi che
considero possono essere disposizioni,
permutazioni, combinazioni con ripetizione
Problemi con ripetizione
• Su un MP3 ci sono 12 canzoni. Se ne ascoltano
tre a caso scelte una alla volta. Quante sono le
terne di canzoni?
• Quanti sono gli anagrammi anche senza
significato della parola CIOCCOLATA?
• In quanti modi posso disporre 6 oggetti
identici in 4 scatole?
Problemi di riepilogo:
• Quante cinquine si possono fare con i 90
numeri del lotto?
• In quanti modi diversi 8 persone si possono
disporre su 5 posti?
• A una gara partecipano 8 concorrenti. In
quanti modi si può presentare la classifica
finale?
Probabilità e genetica
Dalle leggi di Mendel all’ereditarietà poligenica
Un po’ di definizioni
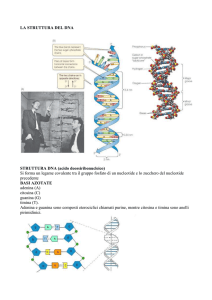
• CROMOSOMA: corpo cellulare di forma costante
contenente i geni disposti in ordine lineare;
• GENE: Unità di ereditarietà, trasmessa con un
cromosoma, in grado di determinare lo sviluppo
di un certo carattere dell’individuo; in termini di
biologia molecolare è la sequenza di un
cromosoma. I geni occupano dunque la stessa
posizione (locus) in cromosomi omologhi;
• ALLELE: una delle varie forme alternative di un
gene.
Le leggi di Mendel
1. I caratteri genetici sono controllati da fattori che
esistono in coppie nei singoli organismi.
2. Quando due fattori diversi, responsabili di un
unico carattere, sono presenti in un dato
individuo, un fattore è dominante sull’altro, che
viene detto recessivo.
3. Durante la formazione dei gameti, i fattori
presenti in coppie si separano, o segregano,
casualmente in modo tale che ciascun gamete
riceve con la stessa probabilità l’uno o l’altro di
essi.
4. Durante la
formazione dei
gameti, le coppie di
fattori segreganti si
assortiscono
indipendentemente
l’una dall’altra.
Frequenza dei genotipi
Osservando campioni di popolazioni, si nota che i
genotipi dominanti non sono necessariamente quelli
più frequenti. Ad esempio, la còrea di Huntington è una
malattia degenerativa dell’encefalo a trasmissione
ereditaria, che è legata all’allele dominante di un gene
del cromosoma umano 18. Tuttavia colpisce solo una
piccolissima parte della popolazione mondiale (dai 3 ai
7 casi su 100 000).
Non si può attribuire la bassa incidenza alla selezione
naturale, perché la malattia colpisce i soggetti tra i 35 e
i 44 anni di età, quando hanno già avuto modo di
riprodursi.
Legge di Hardy-Weinberg
La legge di Hardy-Weinberg trova suo
compimento proprio attraverso questa
domanda: «Come mai se una mutazione è
dominante non siamo tutti soggetti a suddetta
mutazione?».
Punnet pose questa domanda a Hardy, uno dei
più noti matematici inglesi, che dopo poco
tempo trovò la soluzione.
Indipendentemente da lui, anche il tedesco
Weinberg arrivò alle medesime conclusioni.
Legge di Hardy-Weinberg
IPOTESI (POPOLAZIONE IDEALE):
1. Tutti gli individui con qualsiasi genotipo hanno lo
stesso tasso di sopravvivenza e uguale successo
riproduttivo, cioè non c’è selezione.
2. Nessun nuovo allele viene creato o modificato
nella popolazione per mutazione.
3. Non c’è migrazione di individui verso l’esterno o
verso l’interno della popolazione.
4. La popolazione è infinitamente grande.
5. Gli accoppiamenti nella popolazione sono
casuali.
La legge di HardyWeinberg afferma
che le frequenze
degli alleli in un pool
genetico non variano
nel tempo. Se si
considerano ad
esempio due alleli,
dopo un qualsiasi
numero di
generazioni di incroci
casuali le frequenze
genotipiche
rimangono costanti.
In ascissa le frequenze degli alleli (p e q) e in
ordinata le frequenze genotipiche.
Qualche esempio nelle popolazioni
umane
– L’assenza nel sangue del fattore Rh, indicata con Rh-, è
dovuta ad un allele recessivo, indichiamolo con a. Risultano
Rh- gli individui di genotipo aa. Mentre quelli di genotipo
AA, Aa risultano Rh+.
– I gruppi sanguigni sono gestiti da tre diversi alleli che
possono occupare lo stesso locus; l’allele 0 è recessivo,
mentre quelli A e B sono codominanti.
– Lo stesso vale per l’anemia mediterranea o falciforme.
– Altre caratteristiche fisiche (colore degli occhi o dei
capelli, incarnato, altezza) sono regolate da più geni: si parla
di ereditarietà poligenica, e in una popolazione la frequenza
di un certo fenotipo è rappresentata dalla curva gaussiana.