Problema 1
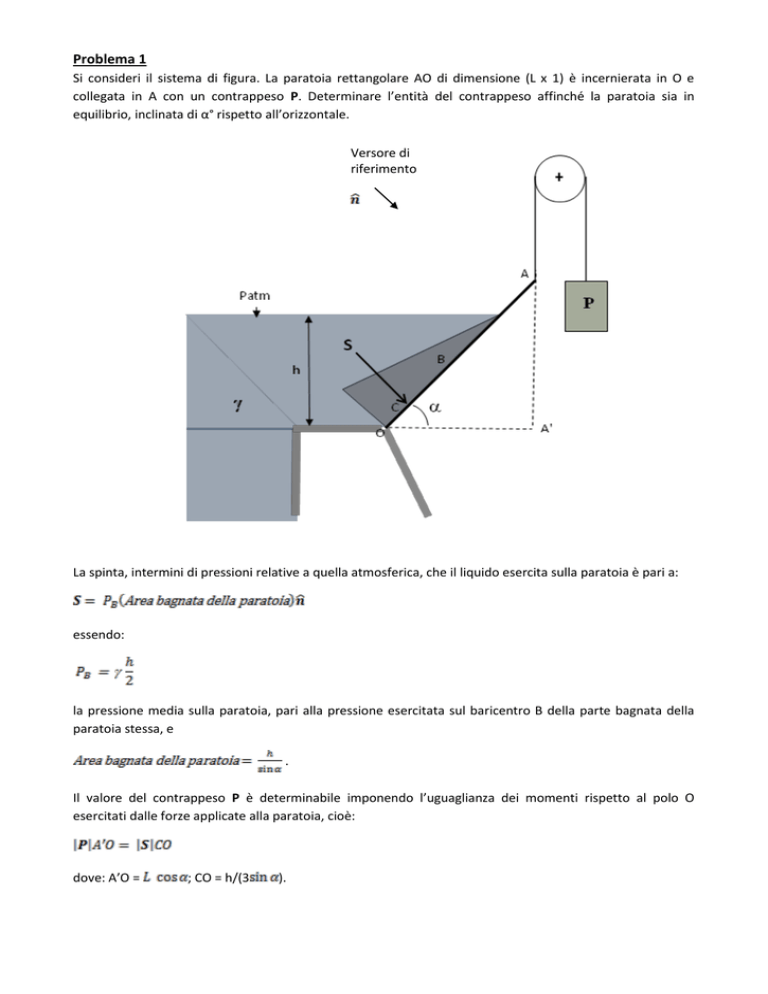
Si consideri il sistema di figura. La paratoia rettangolare AO di dimensione (L x 1) è incernierata in O e
collegata in A con un contrappeso P. Determinare l’entità del contrappeso affinché la paratoia sia in
equilibrio, inclinata di α° rispetto all’orizzontale.
Versore di
riferimento
La spinta, intermini di pressioni relative a quella atmosferica, che il liquido esercita sulla paratoia è pari a:
essendo:
la pressione media sulla paratoia, pari alla pressione esercitata sul baricentro B della parte bagnata della
paratoia stessa, e
.
Il valore del contrappeso P è determinabile imponendo l’uguaglianza dei momenti rispetto al polo O
esercitati dalle forze applicate alla paratoia, cioè:
dove: A’O =
; CO = h/(3
).
Problema 2
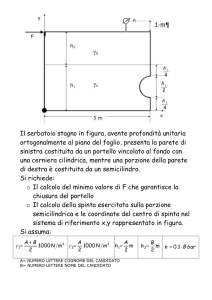
Si consideri il sistema di figura. In una parete laterale del serbatoio è presente un portello rettangolare MN
di dimensioni (MN=L x 1) e incernierato in N. Determinare il modulo della forza F, diretta orizzontalmente
verso l’interno del serbatoio, applicata in M in modo tale che il portello risulti in equilibrio nella posizione
verticale di figura.
Versore di riferimento
h1
L’azione che il portello riceve dal liquido contenuto nel serbatoio è pari alla risultante degli sforzi di
pressione agenti sul portello; l’andamento di tali sforzi, in termini di pressione relativa a quella atmosferica,
è rappresentato dal diagramma di figura (1 + 2). Questa spinta è pari a:
essendo
la pressione media sul portello, pari alla pressione esercitata sul baricentro B del portello stesso.
L’azione può anche essere calcolata come risultante di due spinte parziali, rispettivamente dovute al
contributo 1 e 2 del diagramma delle pressioni rappresentato in figura. Seguendo questo metodo le spinte
parziali sono calcolabili come l’area del rispettivo diagramma delle pressioni parziali agenti sul portello e la
retta di azioni di tali spinte passerà per il baricentro del relativo digramma delle pressioni. Risulta quindi:
e
Il valore del modulo di F, che soddisfa la condizione di equilibrio richiesta, è quindi determinabile dalla
seguente equazione di equilibrio dei momenti rispetto alla cerniera N delle forze applicate al portello, vale
a dire:
dove: BN = L/2; CN = L/3; MN = L.
Problema 3
Si consideri il sistema di figura, nel quale il cassone è diviso in due camere separate da una parete rigida
inclinata di ° rispetto all’orizzontale. Nella parete di separazione è inserito un portello rettangolare MN di
dimensioni (MN=L x 1) e incernierato in N. Determinare il momento risultante rispetto al polo N di tutte le
spinte che agiscono sul portello.
Versore di riferimento
p.c.rel. 2
L sinα
Le spinte idrostatiche che agiscono sul portello, quali risultanti dei campi di pressione relativa (alla
pressione atmosferica) determinati dai liquidi contenuti nelle due camere del cassone, possono essere
calcolate come spinte parziali (vedi il secondo metodo seguito nel Problema 2).
Per quanto riguarda il campo di pressione determinato dal liquido di peso specifico 1, le risultanti parziali
degli sforzi di pressione sono pari a:
e
Per quanto riguarda il campo di pressione determinato dal liquido di peso specifico 2, le risultanti parziali
degli sforzi di pressione risultano essere:
e
Il momento risultante è quindi dato da:
dove: BN = L/2; CN = L/3.
Problema 4
Si consideri il sistema di figura, nel quale una sfera è immersa entro due liquidi. La configurazione di
equilibrio risulta essere quella nella quale la porzione di sferica di volume 1 è immersa nel liquido
superiore, mentre la restante parte della sfera di volume 2 è immersa nel liquido inferiore. Determinare il
peso specifico della sfera.
Versore di
riferimento
Sulla sfera agisce una spinta che è pari alla risultante degli sforzi di pressione esercitati dai due liquidi sulla
superficie della sfera. Nella condizione di equilibrio data è proprio questa spinta che bilancia il peso della
sfera.
Calcolo della spinta S1 risultante sulla superficie della porzione di sfera di volume 1.
Si consideri il volume di controllo ottenuto chiudendo la superficie della calotta sferica superiore con la
superficie piana circolare . L’equazione di equilibrio globale applicata al volume di controllo determina
che:
(1).
La forza di contatto totale sulla superficie del volume di controllo può essere decomposta come:
; inoltre risulta che
.
Sostituendo quanto sopra nella (1), si ottiene:
.
Calcolo della spinta S2 risultante sulla superficie della porzione di sfera di volume 2.
Si consideri il volume di controllo ottenuto chiudendo la superficie della calotta sferica inferiore con la
superficie piana circolare . L’equazione di equilibrio globale applicata al volume di controllo determina
che:
(2).
La forza di contatto totale sulla superficie del volume di controllo può essere decomposta come:
; inoltre risulta che
.
Sostituendo quanto sopra nella (2), si ottiene:
.
La spinta totale che agisce sulla sfera è quindi data da:
dove risulta:
e
;
e
.
Con PB si intende la pressione nel baricentro B della superficie , pressione che è la stessa pressione
determinata sia dal liquido inferiore che dal liquido superiore, poiché la superficie giace sul piano
isobarico di separazione dei due liquidi.
Per cui risulta:
.
Per il galleggiamento della sfera nella condizione di figura deve quindi risultare che il peso della sfera PSfera è
equilibrato dalla spinta che essa riceve dai liquidi, cioè:
ovvero
da cui si può calcolare il peso specifico della sfera come:
dove
.
Problema 5
Si consideri il sistema di figura. Nella parete laterale inclinata del serbatoio è inserito un tappo di forma
tronco conica; la sezione del tappo di volume è immersa nel liquido che riempie il serbatoio e l’area della
superficie ideale di intersezione tra tappo e parete del serbatoio è pari a . Determinare la spinta esercitata
dal liquido sul tappo.
Versori di riferimento
Per risolvere il problema, consideriamo l’equilibrio del volume di controllo costituito dalla porzione di tappo
immersa nel liquido.
L’equazione di equilibrio globale del volume di controllo stabilisce che:
(1).
La forza di contatto totale sulla superficie del volume di controllo può
essere decomposta come:
;
intendendosi con C la risultante degli sforzi di pressione sulla superficie
di base e sulla superficie laterale del tronco di cono; per cui risulta che la
spinta S che si deve determinare è pari a:
.
Sostituendo quanto sopra nella (1), si ottiene:
;
dove risulta:
e
, con
.
Problema 6
Si consideri il sistema di figura, nel quale un cassone è diviso in due camere. In una camera è contenuto un
liquido in pressione, nell’altra un gas. Nell’ambiente in cui è contenuto il gas la pressione assoluta si può
ritenere uguale a Po in ogni punto. Determinare la spinta risultante, dovuta all’azione del liquido e del gas,
sulla cupola semisferica posta nella parete verticale del cassone.
Versori di riferimento
Per determinare la spinta risultante sulla superficie della calotta si può limitare il calcolo alla sola spinta
sulla semisfera determinata dal campo di pressione prodotto dal liquido, purché si considerino le pressioni
relative alla pressione Po.
Per risolvere il problema, consideriamo quindi l’equilibrio del volume di controllo costituito dalla semisfera
immersa nel liquido.
L’equazione di equilibrio globale del volume di controllo stabilisce che:
(1).
La forza di contatto totale sulla superficie del volume di
controllo può essere decomposta come:
; la spinta S che si deve determinare è pari a:
.
Sostituendo quanto sopra nella (1), si ottiene:
;
dove risulta:
e
,
con PB pressione sul baricentro B di , espressa in termini di pressione relativa alla pressione del gas Po, vale
a dire:
.