clicca qui

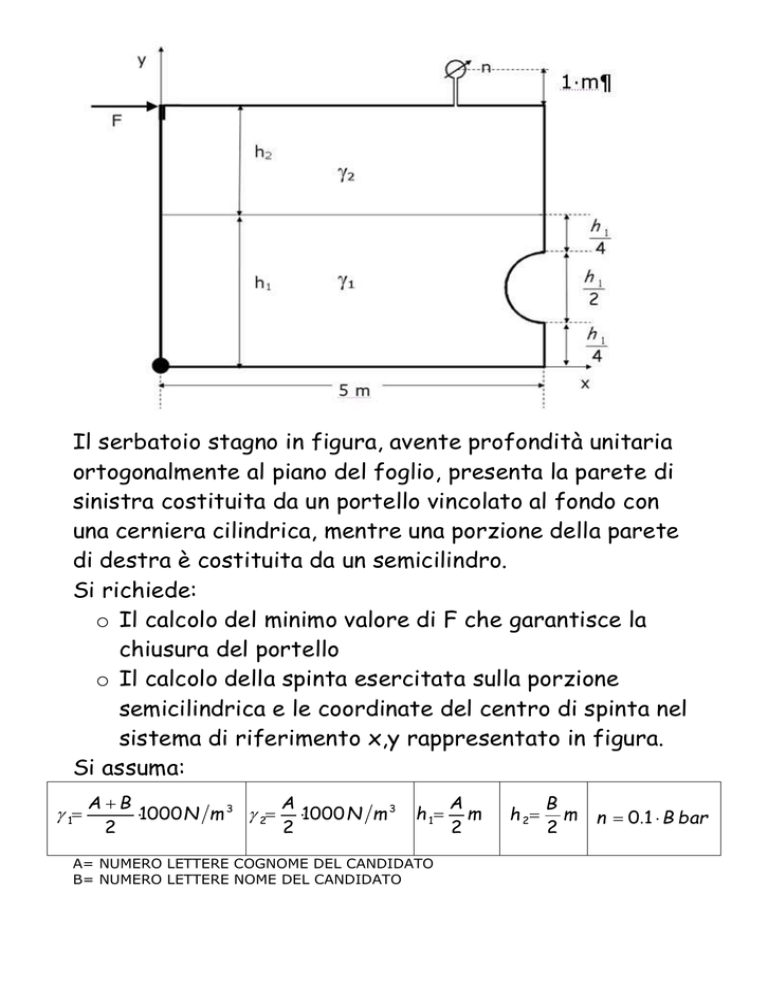
Il serbatoio stagno in figura, avente profondità unitaria
ortogonalmente al piano del foglio, presenta la parete di
sinistra costituita da un portello vincolato al fondo con
una cerniera cilindrica, mentre una porzione della parete
di destra è costituita da un semicilindro.
Si richiede:
o Il calcolo del minimo valore di F che garantisce la
chiusura del portello
o Il calcolo della spinta esercitata sulla porzione
semicilindrica e le coordinate del centro di spinta nel
sistema di riferimento x,y rappresentato in figura.
Si assuma:
 1
A B
A
1000 N m 3  2 1000 N m 3
2
2
h 1
A= NUMERO LETTERE COGNOME DEL CANDIDATO
B= NUMERO LETTERE NOME DEL CANDIDATO
A
m
2
h 2
B
m n  0.1  B bar
2
CORSO DI LAUREA IN INGEGNERIA CIVILE
ANNO ACCADEMICO 2011-2012
INSEGNAMENTO DI IDRAULICA
PRIMO ACCERTAMENTO IN AULA
(IDROSTATICA)
I due serbatoi rappresentati in figura (quello di sinistra in pressione, quello di
destra a pelo libero) sono separati da una paratoia cilindrica che può ruotare in
senso orario intorno alla cerniera C.
La sfera S in PVC (=15000 N/m3) è collegata solidarmente alla paratoia in
corrispondenza della cerniera C.
Si calcoli il massimo valore che può assumere il peso specifico 2 prima che la
paratoia si apra.
In queste condizioni si determinino le coordinate del centro di spinta del fluido
di peso specifico 2 sulla paratoia cilindrica nel sistema di riferimento X,Y
indicato in figura.
Si assuma profondità della paratoia unitaria e:
n
A
bar
10
h  A  B m
Dove: A= Numero Lettere del Nome
1 
A B
 1000 N / m 3
2
B= Numero lettere del Cognome
Esempio:
Nome: Francesco
y
Cognome: Rossi
A=9 : B= 5
n
9
 0.9 bar
10
1 
h  14 m
95
 1000  7000N / m 3
2
7m
x