TECNICHE DI PILOTAGGIO DELL’INVERTER TRIFASE
1
NOZIONI DI BASE
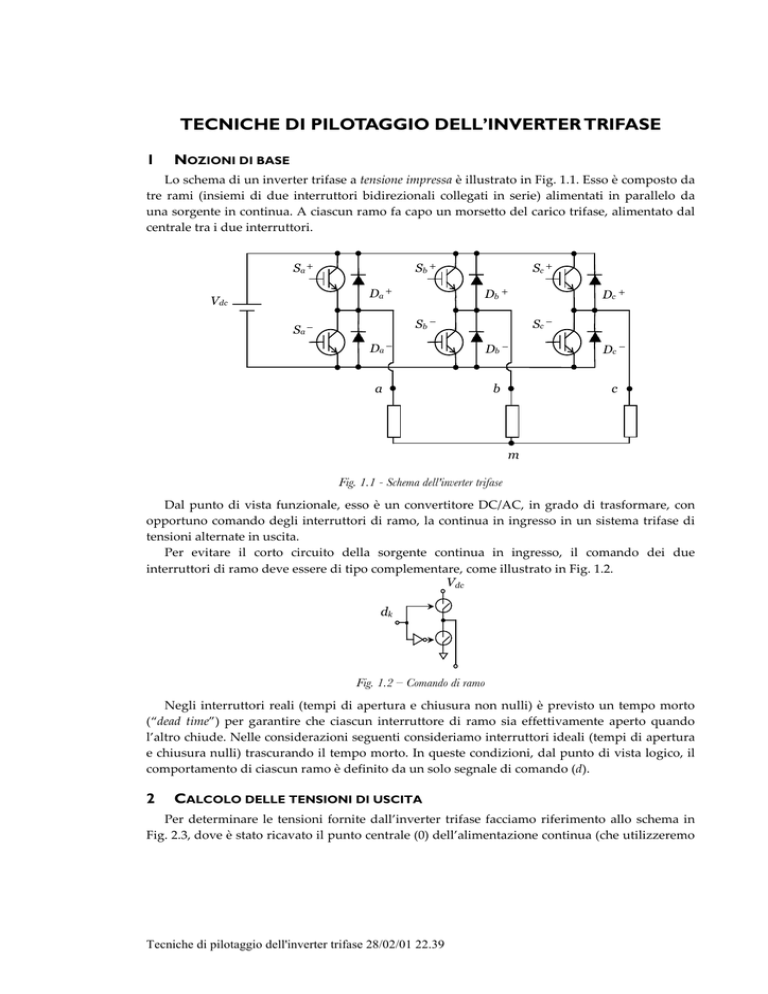
Lo schema di un inverter trifase a tensione impressa è illustrato in Fig. 1.1. Esso è composto da
tre rami (insiemi di due interruttori bidirezionali collegati in serie) alimentati in parallelo da
una sorgente in continua. A ciascun ramo fa capo un morsetto del carico trifase, alimentato dal
centrale tra i due interruttori.
Sa +
Sb +
Da +
Vdc
Sc +
Db +
Dc +
Sc −
Sb −
Sa −
Da −
Db −
Dc −
a
b
c
m
Fig. 1.1 - Schema dell'inverter trifase
Dal punto di vista funzionale, esso è un convertitore DC/AC, in grado di trasformare, con
opportuno comando degli interruttori di ramo, la continua in ingresso in un sistema trifase di
tensioni alternate in uscita.
Per evitare il corto circuito della sorgente continua in ingresso, il comando dei due
interruttori di ramo deve essere di tipo complementare, come illustrato in Fig. 1.2.
Vdc
dk
Fig. 1.2 – Comando di ramo
Negli interruttori reali (tempi di apertura e chiusura non nulli) è previsto un tempo morto
(“dead time”) per garantire che ciascun interruttore di ramo sia effettivamente aperto quando
l’altro chiude. Nelle considerazioni seguenti consideriamo interruttori ideali (tempi di apertura
e chiusura nulli) trascurando il tempo morto. In queste condizioni, dal punto di vista logico, il
comportamento di ciascun ramo è definito da un solo segnale di comando (d).
2
CALCOLO DELLE TENSIONI DI USCITA
Per determinare le tensioni fornite dall’inverter trifase facciamo riferimento allo schema in
Fig. 2.3, dove è stato ricavato il punto centrale (0) dell’alimentazione continua (che utilizzeremo
Tecniche di pilotaggio dell'inverter trifase 28/02/01 22.39
2
2 Calcolo delle tensioni di uscita
come potenziale di riferimento) e si è considerato il caso generale di un carico collegato a stella
con neutro isolato.
d1
d2
Vdc
2
d3
Da +
Db +
Dc +
Da −
Db −
Dc −
b
c
0
Vdc
2
Vab
a
Va0
Vam
m
Vm0
Fig. 2.3 - Tensioni di uscita dell’inverter trifase
•
Si possono distinguere:
le tensioni di ramo Va0, Vb0, Vc0, che sono direttamente individuate dal comando di ramo:
d1 = 0 → V a 0 =
d2 = 1 → Vb0
d 2 = 0 → V b0 =
d3 = 1 → Vc 0
•
V dc
;
2
V
= dc ;
2
V dc
=
;
2
d1 = 1 → V a 0 =
d3 = 0 → Vc0 =
V dc
2
V dc
2
V dc
2
(2.1)
le tensioni concatenate Vab, Vbc, Vca, ottenibili come combinazione delle tensioni di ramo:
V ab = V a0 − V b0
V bc = V b0 − V c 0
(2.2)
V ca = V c 0 − V a0
•
•
le tensioni di fase del carico Vam, Vbm, Vcm;
la tensione del centro stella del carico rispetto al potenziale di riferimento Vm0.
Per quanto concerne l’individuazione delle tensioni di fase, esse possono essere espresse
come:
V am = V a0 − V m0
V bm = V b0 − V m0
V cm = V c 0 − V m 0
In queste relazioni occorre determinare il potenziale (incognito) del centro stella.
(2.3)
Scomposizione in serie di Fourier
3
Sommando membro a membro si ricava:
V am + V bm + V cm = (V a 0 + V b0 + V c 0 ) − 3V m0
(2.4)
Nell’ipotesi di carico trifase simmetrico collegato a stella con neutro isolato, è facile dimostrare1
che la somma delle tensioni di fase è nulla:
V am + V bm + V cm = 0
(2.5)
da cui si ricava:
V mo =
1
(V a0 + Vb0 + Vc0 )
3
(2.6)
Pertanto, note le tensioni di ramo (dal comando), si può calcolare il potenziale del centro
stella con la (2.6) e quindi le tensioni di fase dalle (2.3).
In funzione dello stato logico (0 o 1 ) del comando dei tre rami, l’inverter trifase è in grado di
applicare 8 diverse configurazioni di tensione d’uscita, delle quali 2 corrispondenti a tensione
nulla (stati 0 e 7) e le altre 6 a tensione non nulla (stati 1..6).
La più semplice modalità di comando dell’inverter trifase prevede l’applicazione in
sequenza delle 6 configurazioni non nulle di tensione: si tratta del comando ad onda quadra (o sixstep) illustrato nel paragrafo seguente.
001
010
100
011
101
000
110
111
Fig. 2.4 - Stati dell’inverter trifase
1
stato
0
1
2
3
4
5
6
7
d1
0
1
1
0
0
0
1
1
d2
0
0
1
1
1
0
0
1
d3
0
0
0
0
1
1
1
1
Tab. 2.1 – Stati e rispettivi
comandi di ramo
Nelle condizioni indicate si può scrivere: Vam=Z⋅ia, Vbm=Z⋅ib, Vcm=Z⋅ic, che sommando m. a m. fornisce: Vam+Vbm+Vcm=Z⋅(ia +ib
+ic)=0.
4
3
3 Comando ad onda quadra (Six Step)
COMANDO AD ONDA QUADRA (SIX STEP)
Va0
Vdc
2
Sa+
Sa+
π
Sa– 2π
−
ω1t
Vdc
2
Vb0
Sb+
Sb–
Sb–
ω1t
Vc0
Sc+
Sc–
Sc–
ω1t
Fig. 3.5 - Tensioni di uscita riferite al punto centrale del bus DC
Vab
Vdc
0
π
2π
ω1t
–Vdc
Vbc
ω1t
Vca
ω1t
Fig. 3.6 - Tensioni di uscita concatenate
Scomposizione in serie di Fourier
3.1
5
Scomposizione in serie di Fourier
3.1.1
Tensioni di uscita riferite al punto centrale del bus DC
1
1
1
sin(ω1 t ) + 3 sin(3ω1t ) + 5 sin(5ω1t ) + 7 sin(7 ω1t ) +...
v a0 (t ) =
4 V dc
π 2
vb0 (t ) =
4 Vdc
2π 1
1
2π 1
2π
+ sin(3ω1t ) + sin 5ω1t +
+ sin 7 ω1t −
+...
sin ω1t −
π 2
3 3
5
3 7
3
v c 0 (t ) =
4 V dc
4π 1
1
4π 1
4π
+ sin(3ω1t ) + sin 5ω1t +
+ sin 7 ω1t −
+...
sin ω1t −
3 3
5
3 7
3
π 2
(3.7)
Sono presenti soltanto le armoniche dispari.
k = 6 j + 1 sequenze dirette
k = 6 j + 3 sequenze omopolari
k = 6 j + 5 sequenze inverse
3.1.2
j = 0, 1, 2, ...
Tensioni di uscita concatenate
π 1
π 1
π
sin ω1t + − sin 5ω1t + − sin 7 ω1t + + K
6
5
6
7
6
vab (t ) =
4 3 Vdc
π 2
vbc (t ) =
4 3 Vdc
π 2π 1
π 2π 1
π 2π
sinω1t + − − sin5 ω1t + +
− sin7 ω1t + − +L
6 3 5
6 3 7
6 3
π 2
vca (t ) =
π 4π 1
π 4π 1
π 4π
4 3 Vdc
sinω1t + − − sin5 ω1t + + − sin7 ω1t + − + K
π 2
6 3 5
6 3 7
6 3
(3.8)
Non sono presenti le sequenze omopolari nelle tensioni concatenate.
3.1.3
Tensione del centro stella del carico riferita al punto centrale del bus DC
v m0 (t ) =
1
(v a0 (t ) + v b0 (t ) + v c 0 (t ))
3
(3.9)
6
3 Comando ad onda quadra (Six Step)
v m0 (t ) =
4 V dc
π 2
1
1
1
3 sin(3ω 1 t ) + 9 sin(9ω 1 t ) + 15 sin(15ω 1 t ) + L
(3.10)
Sono presenti soltanto le armoniche multiple di tre.
3.1.4
Tensioni di fase del carico
v am ( t ) =
4 V dc
π 2
1
1
sin( ω 1 t ) + 5 sin( 5ω 1 t ) + 7 sin(7 ω 1 t ) + L
vbm (t ) =
4 Vdc
π 2
2π 1
2π 1
2π
sin ω 1t − 3 + 5 sin 5ω 1t + 3 + 7 sin 7 ω 1t − 3 + L
v cm (t ) =
4 V dc
4π 1
4π 1
4π
sin ω 1 t −
+ sin 5ω 1 t +
+ sin 7 ω 1 t −
+ L
π 2
3 5
3 7
3
(3.11)
Non sono presenti le armoniche multiple di tre nelle tensioni di fase.
Riepilogo delle nozioni fondamentali:
ω1
.
2π
- Non è possibile controllare l’ampiezza della fondamentale:
- È possibile controllare la frequenza fondamentale f 1 =
-
4 V dc
≅ 0.636 Vdc
ampiezza 1a armonica della tensione di fase del carico 1 Vˆ f =
π 2
4 Vdc
3 ≅ 1.1 Vdc
ampiezza 1a armonica della tensione di linea del carico 1 Vˆ l =
π 2
ampiezza 1a armonica della tensione di uscita dell’inverter (riferita al centrale del bus
4 V dc
.
DC) 1 Vˆ f 0 =
π 2
Rappresentazione vettoriale della tensione di uscita
3.2
7
Rappresentazione vettoriale della tensione di uscita
Va0
1 1
Vdc
2
1 π
2π
0 0 0
−
Vdc
2
ω1t
Vb0
1
1
1
0 0
ω1t
0
Vc0
1
1
1
ω1t
0 0 0
stato
6
1
2
3
4
5
Fig. 3.7 – Stati dell’inverter e tensioni ai morsetti nel comando “six-step”
Vm0
V dc
6
2π
π
Vam
100
101
ω 1t
2Vdc
3
110
010
001
ω1t
011
Vbm
ω 1t
Vcm
ω1t
stato
6
1
2
3
4
5
Fig. 3.8 – Stati dell’inverter e tensioni sul carico nel comando “six- step”
Se si considerano le 6+2 possibili configurazioni delle tensioni di fase applicate al carico
dall’inverter trifase (nelle figure precedenti sono riportate le 6 configurazioni non nulle), e si
applica a ciascuna di esse la trasformazione di fasi2 (abc)→(α,β), si ottengono altrettanti vettori di
spazio (ciascuno caratterizzato da una coppia di componenti α,β) la cui rappresentazione nel
piano complesso è indicata in figura:
2
Trasformazione a potenza di fase costante.
8
4 Tecniche di modulazione PWM
b
r
V3 (010)
r
V4
(011)
r
V2 (110)
β
(000)
r
Vo
(111)
r
V7
r
V5 (001)
2
V
3 dc
α≡a
r
V1 (100)
1
V
3 dc
r
V6
(101)
c
Fig. 3.9 - Esagono delle tensioni di uscita dell’inverter trifase
Tale rappresentazione, nota come “esagono delle tensioni di uscita dell’inverter trifase”, consente
di valutare, per ciascuna configurazione del comando, le tensioni applicate al carico sia in
termini di componenti α,β che in termini di tensioni trifasi (queste ultime sono ottenibili come
le componenti di ciascun vettore sugli assi 123 sfasati di 2π/3).
stato
0
1
2
3
4
5
6
7
vettore di
spazio
r
V0
r
V1
r
V2
r
V3
r
V4
r
V5
r
V6
r
V7
d1
d2
d3
0
0
0
1
0
0
1
1
0
0
1
0
0
1
1
0
0
1
1
0
1
1
1
1
Tab. 3.2 – Stati, comandi di ramo e vettori di spazio
I sei vettori della tensione di uscita dell’inverter delimitano altrettanti settori angolari di π/3
(“sestanti”) la cui individuazione è alla base di una tra le più importanti tecniche di
modulazione dell’inverter trifase, la modulazione dei vettori di spazio (SV-PWM) presentata nel
seguito.
4
4.1
TECNICHE DI MODULAZIONE PWM
Modulazione seno-triangolo (S∆-PWM)
In questo tipo di modulazione i componenti statici vengono commutati negli istanti di
intersezione di due funzioni periodiche di frequenza diversa (portante e modulante). In questo
modo è possibile sintetizzare delle tensioni di uscita (Va0, Vb0 e Vc0) che, a bassa frequenza, hanno
Modulazione seno-triangolo (S∆-PWM)
9
lo stesso contenuto armonico (stessa forma d'onda) della funzione di riferimento a frequenza
minore. Come portante è di solito usata una funzione triangolare (Vt) con frequenza angolare ωt
ed un valore di picco V̂t .
Come modulanti si usano tre tensioni sinusoidali di frequenza pari a quella desiderata per la
fondamentale della tensione di uscita:
V a*0 (t ) = Vˆ s sin(ω 1 t )
V b*0 (t ) = Vˆ s sin(ω 1 t − 2π 3 )
(4.12)
V c*0 (t ) = Vˆ s sin(ω 1 t − 4π 3)
Parametri fondamentali
Vˆ
M= s
indice di modulazione
Vˆ
t
ω
P= t
ω1
rapporto tra le frequenze
Tecnica di commutazione
se V a*0 > Vt allora poni Sa+ “on” e Sa‒ “off”
se invece V a*0 < Vt allora poni Sa‒ “on” e Sa+ “off”
Vt
Va*0
Va0
Fig. 4.10 – Modulazione S∆-PWM
Vt
*
Vao
ω1 t
0
π
2π
Fig. 4.11 - Portante e modulante nella S∆-PWM con p = 12, M = 0.6
10
4 Tecniche di modulazione PWM
Va0
tensione fondamentale
V dc
2
ω1 t
π
0
2π
Fig. 4.12 - Tensione di uscita (fase a) riferita al punto centrale del bus DC.
Vab
tensione fondamentale
Vdc
π
0
ω1 t
2π
Fig. 4.13 - Tensione concatenata
4.1.1
Scomposizione in serie di Fourier
Σ
V a0 ( t ) = M
2V dc
+
π
V dc
2V dc
cos(α ) +
π
2
∞
±∞
∞
π
π
∑ J 0 k M 2 sin k 2 cos(kω t t )+
k =1
1 π
π
J n k M sin(k + n) cos(kω t t + nα )
2
2
k =1 n= ±1 k
∑∑
(4.13)
dove:
α = ω1t
J0, ... , Jn: funzioni di Bessel del primo ordine.
• Il primo termine rappresenta la tensione fondamentale che è direttamente proporzionale
all'indice di modulazione se M < 1.
• Il secondo termine rappresenta le componenti armoniche alla frequenza della portante e suoi
multipli. Non esistono armoniche la cui frequenza è multiplo pari della frequenza della
portante: sin(k π / 2 ) = 0 se k è pari.
Modulazione seno-triangolo (S∆-PWM)
11
• Il terzo termine rappresenta le bande di armoniche centrate sulle frequenze multiple
della frequenza della portante. In accordo con il termine sin[(k + n ) π / 2 ] si ha:
- per k dispari, la banda presenta solo armoniche pari;
- per k pari, la banda presenta solo armoniche dispari.
Poiché l'armonica dominante si ha per ω = ωt, si prende un rapporto di frequenze p multiplo
di tre, in modo tale che l'armonica dominante formi una sequenza omopolare (terne di correnti
omopolari non possono circolare).
tensione
p.u.
ω1
1
0.6
0.2
ω1
ωt
2ωt
3ωt
ω
Fig. 4.14 - Tipico spettro della modulazione S∆-PWM (M = 0.8)
k
V̂ a 0
V dc
0.5
0.4
k = 1 (fondamentale)
0.3
k = 2p± 1
0.2
k = p±2
0.1
k = 3p± 2
0
0.2
0.4
0.6
0.8
indice di modulazione
1.0
M
Fig. 4.15 - Ampiezza relativa delle armoniche in funzione dell'indice di modulazione
(tensione di uscita dell’inverter riferita al centrale del bus DC).
Per M = 1, si ha il massimo valore della tensione fondamentale, che è soltanto il 78.5% della
massima tensione fondamentale che si può avere dall'inverter (con la modulazione six step):
1 ˆ
V a0(SIX −STEP ) π
V
4 V dc
1 ˆ
→
= = 0.785 3
V a 0( M =1) = dc ; 1Vˆ a 0(SIX −STEP ) =
(4.14)
1 ˆ
2
π 2
4
V a 0 ( M =1)
3
Queste relazioni valgono anche per la tensione di fase del carico, la cui prima armonica ha la stessa ampiezza della tensione di
uscita dell’inverter riferita al centrale del DC bus.
12
4 Tecniche di modulazione PWM
4.1.2
Sovra-modulazione ( M > 1 )
Per sfruttare meglio la tensione continua disponibile si può operare con M > 1. All'aumentare
di M alcuni impulsi vengono eliminati e per un certo valore di M si torna alla modulazione “six
step” con lo svantaggio di ritrovare le armoniche a bassa frequenza nella tensione di uscita.
Va0*
Vt
Va0
Vdc
2
ω1 t
0
ω1 t
0
π
2π
π
2π
Fig. 4.16 - S∆-PWM con p = 12, M = 1.1
Va0
*
Va0
Vdc
2
Vt
ω1 t
0
ω1 t
0
π
π
2π
2π
Fig. 4.17 - S∆-PWM con p = 12, M = 5
1
V̂l
Vdc
TEORICO
1.10
0.866
lineare sovramodulazione
1
onda quadra
(six steps)
3.24
M
Fig. 4.18 - Ampiezza della 1a armonica della tensione concatenata in funzione dell'indice di modulazione (p = 15)
Modulazione seno-triangolo (S∆-PWM)
13
In pratica, quando un interruttore statico viene commutato, non è possibile commutarlo
ulteriormente prima di un determinato intervallo di tempo che dipende dal suo tempo di
“recovery”. Cioè esiste una durata minima d'impulso nella forma d'onda della tensione. Negli
inverter è quindi sempre presente un circuito di “lockout”. Ciò determina dei salti di tensione
all'estremità della zona lineare e nella zona di sovra-modulazione.
Vk
Vdc 2 1.2
k=1
diminuzione
degli impulsi
1.0
(passaggio all'onda quadra)
0.8
diminuzione
degli impulsi
0.6
0.4
k=3
0.2
0
k=5
k=7
0.2
0.4 0.6
0.8 1.0 1.2
modulazione lineare
1.4 1.6
1.8
2.0
M
sovramodulazione
Fig. 4.19 - Andamento reale delle tensioni armoniche in funzione dell'indice di modulazione,
in presenza del circuito di lockout
4.1.3
Distorsione della modulante
Per sfruttare meglio la tensione continua disponibile si può inserire una distorsione nelle
tensioni di riferimento modulanti. In genere viene usata una terza armonica in quanto, essendo
omopolare, non influisce sulla corrente del carico4:
V a*0 (t ) = Vˆ S1 sin(ω 1 t ) + Vˆ S 3 sin(3ω 1 t )
(4.15)
Con Vˆ S 3 = Vˆ t 6 , l’ampiezza della fondamentale della tensione di uscita può raggiungere il
valore 1.15 Vdc/2.
Vˆ
Vˆ S 3 = t
6
M=
Vˆ S1
Vˆ
t
4
Nelle tensioni di fase non ci sono terze armoniche poiché, come visto nel 6-step, anche se nella vao c’è la terza e le multiple,
queste sono anche nella vmo e facendo vam=vao–vmo si eliminano. Anche nelle concatenate le terze armoniche si elidono (ad es.
vab=vao–vbo). Quindi anche con collegamento a triangolo non si hanno tensioni impresse e quindi correnti di terza armonica.
14
4 Tecniche di modulazione PWM
*
Va0
Va0
Vt
Vdc
2
ω1 t
0
ω1 t
0
π
2π
π
2π
Fig. 4.20 - S∆-PWM con p = 12, M = 1.1: terza armonica nella tensione di riferimento
1
V̂ f
TEORICO
Vdc
con
2
= 0.636
π
0.57
3a
armonica
0.5
lineare
1
sovramodulazione
3.24
onda quadra
(six steps)
M
Fig. 4.21 - Ampiezza della 1a armonica della tensione di fase (collegamento a stella del carico
in funzione dell’indice di modulazione ( p = 15 )
4.2
4.2.1
Modulazione dei vettori di spazio (SV-PWM)
Introduzione
La tecnica di modulazione dei vettori di spazio fa riferimento alla rappresentazione della
tensione di uscita dell’inverter trifase illustrata al paragrafo 3.2. In base ad essa i vettori di uscita
dell’inverter possono essere espressi con notazione complessa nel riferimento bifase α,β come
segue (α ⇒ Re, β ⇒ jIm):
r
Vi = Vαi + jVβi
(4.16)
Dalla Fig. 3.9, ponendo V = 2 / 3V dc , si ricavano quindi le seguenti espressioni (nel caso dei
vettori non nulli):
r
V1 :
V α1 = V
r
, V1 = V
Vβ1 = 0
(4.17)
Modulazione dei vettori di spazio (SV-PWM)
r
V2 :
r
V3 :
r
V4 :
r
V5 :
r
V6 :
15
V α 2 = V cos (π / 3) r
1
3
, V2 = + j
V
2
2
Vβ 2 = V sin (π / 3)
V α 3 = −V cos (π / 3) r
1
3
, V3 = − + j
V
2
Vβ 3 = V sin (π / 3 )
2
V α 4 = −V
r
, V 4 = −V
Vβ 4 = 0
V α 5 = −V cos (π / 3) r
1
3
, V5 = − − j
V
2
2
Vβ 5 = −V sin (π / 3 )
V α 6 = −V cos (π / 3) r
1
3
, V6 = − j
V
2
2
Vβ 6 = V sin (π / 3 )
r
Nella modulazione dei vettori di spazio, la sintesi del generico vettore di tensione ( V * ,
“tensione di riferimento”) avviene modulando tra i vettori di uscita dell'inverter che delimitano
ciascun sestante ed il vettore nullo, come illustrato in Fig. 4.22.
r
Vi + 1
r
V*
r
Vi
Fig. 4.22 - Sintesi del vettore di tensione nello SV-PWM
4.2.2
Calcolo del settore angolare
Per il calcolo del settore angolare si consideri il sistema di assi xyz tra loro sfasati di 2π/3 e
r
r
disposti in modo da rappresentare le bisettrici rispettivamente dei settori delimitati da V 2 − V 3
r
r
r
r
(asse x), V 4 − V 5 (asse y) e da V 6 − V1 (asse z), Fig. 4.23.
r
Le proiezioni su xyz del generico vettore di tensione V * da sintetizzare in un determinato
istante sono date da:
V x = Vβ
1
Vβ −
2
1
V z = −V β cos(π / 3) + V α cos(π / 6 ) = − Vβ +
2
V y = −Vβ cos(π / 3) − V α cos(π / 6 ) = −
3
Vα
2
3
Vα
2
(4.18)
È facile comprendere come il valore istantaneo del segno di ciascuna proiezione sia in
relazione diretta ed univoca con l’appartenenza del vettore di tensione ad uno dei sestanti
delimitati dai vettori di uscita dell’inverter trifase.
16
4 Tecniche di modulazione PWM
r r
Ad esempio, finché il vettore di tensione appartiene al settore delimitato da V1 − V2 , come è il
caso illustrato in Fig. 4.23, sarà certamente Vx ≥ 0 , Vy < 0 e Vz ≥ 0.
Trascurando il caso singolare di vettore nullo (Vx =Vy =Vz = 0) è facile ricavare la seguente la
seguente tabella5:
sestante
r
r
V1 − V 2
r
r
V2 − V3
r
r
V3 − V4
r
r
V4 − V5
r
r
V5 − V6
r
r
V 6 − V1
non applicabile
Vx
Vy
Vz
≥0
<0
≥0
>0
≤0
≤0
≥0
≥0
<0
≤0
>0
≤0
<0
≥0
≥0
≤0
≤0
>0
>0
>0
>0
<0
<0
<0
Tab. 4.3 – Sestanti in funzione delle componenti xyz
x
r
V3 (010)
r
V2 (110)
β
r
V*
Vx
r
V4
Vy
(011)
α
r
V1 (100)
Vz
r
V5 (001)
y
Vx ≥ 0,
Vy < 0,
Vz ≥ 0
r
V6
(101)
z
Fig. 4.23 - Relazione tra le componenti xyz ed i settori angolari
Trascurando le uguaglianze ed attribuendo il valore numerico “1” se il segno di una
componente è positivo, “0” se negativo, dalla tabella precedente si può ricavare una codifica
univoca come segue:
LSBit
sestanti
r
r
V1 − V 2
r
r
V2 − V3
MSBit
codifica
sgn(Vx)
sgn(Vy)
sgn(Vz)
sgn(Vx)+2·sgn(Vy)+4·sgn(Vz)
1
1
0
3
1
0
0
1
5
Si osservi che le proiezioni xyz del vettore di tensione costituiscono, con la rotazione di questo, una terna trifase nel tempo, e
che, pertanto, in ogni istante, non può verificarsi il caso in cui si abbiano tutte le proiezioni contemporaneamente positive o
negative.
Modulazione dei vettori di spazio (SV-PWM)
r
V3
r
V4
r
V5
r
V6
r
− V4
r
− V5
r
− V6
r
− V1
17
1
0
1
5
0
0
1
4
0
1
1
6
0
1
0
2
Tab. 4.4 – Codifica dei sestanti in funzione delle componenti xyz
x
r
V3 (010)
r
V2 (110)
β
1
5
r
V4
(011)
3
4
2
r α
V1 (100)
6
r
V5 (001)
y
r
V6
(101)
z
Fig. 4.24 - Codifica dei sestanti
4.2.3
Sintesi del vettore di tensione
r
Con riferimento alla Fig. 4.22, la sintesi del generico vettore di tensione ( V * ) avviene
r
modulando tra i vettori di uscita dell'inverter che delimitano ciascun sestante dell’esagono ( Vi e
r
r
r
Vi +1 ) ed il vettore nullo ( V0 ). Essendo V0 = 0 , ed indicando con T1 e T2 i tempi di applicazione
r
r
dei vettori non nulli (rispettivamente T1 di Vi e T2 di Vi +1 ) si può scrivere:
T
∫ (V
*
α
)
+ jV β* dt =
0
T1
∫ (V
αi
)
T1 +T2
+ jV βi dt +
0
∫ (V α (i +1) + jVβ(i+1) )dt
(4.19)
T1
Scomponendo nella parte reale ed immaginaria:
T1
T1 +T2
T
V α* dt = V αi dt + V α (i +1) dt
0
T1
0
T
T1
T1 +T2
*
Vβ dt = V βi dt + V β(i +1) dt
0
T1
0
∫
∫
∫
∫
∫
(4.20)
∫
e risolvendo gli integrali (i cui argomenti sono costanti nel passo di campionamento) si ottiene:
18
4 Tecniche di modulazione PWM
V ai T1 + V a(i +1)T2 = V α* T
*
Vβi T1 + V β(i +1)T2 = V β T
(4.21)
Questo sistema può essere risolto, in ogni settore, per calcolare i tempi di applicazione dei
vettori non nulli. Ad esempio, procedendo con il metodo di Kramer si ha:
Vα*T Vα (i + 1)
T1 =
Vβ*T
Vβ(i + 1)
∆
T2 =
Vαi
Vα*T
Vβi
Vβ*T
∆=
∆
Vαi
Vα (i +1)
Vβi
Vβ(i +1)
= Vαi Vβ(i + 1) − Vβi Vα (i +1)
(4.22)
mentre il tempo di applicazione del vettore nullo si può calcolare dalla:
T0 = T − (T1 + T2 )
(4.23)
In ciascun settore la sequenza di applicazione dei vettori non nulli è arbitraria, come pure la
scelta del vettore nullo (0 oppure 7) da applicare.
Al riguardo vengono individuati due metodi principali, noti come SV-PWM simmetrico ed
asimmetrico, in base al fatto che il “pattern” dei segnali di comando di ciascun ramo presenti o
meno un andamento simmetrico.
4.2.4
SV-PWM simmetrico
Nello SV-PWM simmetrico i gradi di libertà presenti nell’applicazione dei vettori di tensione
nulla vengono risolti in modo da generare una configurazione (“pattern”) dei segnali di
comando di tipo simmetrico nel periodo di PWM (nella figura seguente è illustrato il caso del
settore (3) ).
(3)
CMPR3
CMPR2
CMPR1
d3
0
0
0 1
d2
0
0
1 1
d1
0
1
1
1
T0
2
T1
T2
T0
2
T0
2
T2
T1
T0
2
T
TPWM
Fig. 4.25 - SV-PWM simmetrico
Tale metodo permette di minimizzare, in ciascun passo di campionamento, le commutazioni
degli interruttori statici. Infatti le commutazioni sono minimizzate se, nel passaggio da un
vettore al successivo, si ha un solo interruttore statico che cambia stato.
Modulazione dei vettori di spazio (SV-PWM)
19
In termini di vettore nullo, tale condizione porta all'impiego, in ogni passo di
campionamento, di entrambe le configurazioni (0 e 7) suddividendo a metà il tempo T0 ed
applicando tensione nulla all'inizio ed alla fine del passo.
In questo modo si arriva a determinare un pattern dei segnali di comando dell'inverter
trifase di tipo simmetrico, con una fase di “andata” ed una di “ritorno” corrispondenti, nella
pratica implementazione, ai fronti di salita e discesa di una portante triangolare di periodo pari
al periodo di PWM.
Con tali osservazioni, la sequenza di applicazione dei vettori di uscita dell'inverter nei sei
sestanti sarà la seguente:
andata →
sestante
T0/2
(3)
r
V0 Ê
(1)
r
V0 Ê
(5)
r
V0 Ê
(4)
r
V0 Ê
(6)
r
V0 Ê
(2)
r
V0 Ê
T1 (Vi)
r
V1 Æ
r
Å V1
← ritorno
T2 (Vi+1)
r
V3 Æ
r
Å V3
r
V3 Æ
r
Å V3
r
V5 Æ
r
Å V5
r
V5 Æ
r
Å V5
r
V2 Æ
r
Å V2
r
V2 Æ
r
Å V2
r
V4 Æ
r
Å V4
r
V1 Æ
r
Å V1
r
V4 Æ
r
Å V4
r
V6 Æ
r
Å V6
r
V6 Æ
r
Å V6
T0/2
r
Ë V7
r
Ë V7
r
Ë V7
r
Ë V7
r
Ë V7
r
Ë V7
Tab. 4.5 – Tempi di applicazione dei vettori di spazio nei diversi sestanti
L'applicazione delle relazioni per il calcolo dei tempi di applicazione dei vettori non nulli,
tenuto conto della sequenza indicata nelle precedenti tabelle, fornisce i seguenti risultati:
sestante
∆
T1
T2
(3)
3 2
V
2
K 2Vα* − K1Vβ* = −Z
2 K1Vβ* = X
− K 2 V α* + K 1Vβ* = Z
K2Vα* + K1Vβ* = Y
(1)
−
3 2
V
2
(5)
3 2
V
2
2 K 1 Vβ* = X
− K 2 V α* − K 1 Vβ* = −Y
(4)
3 2
V
2
− 2K 1 Vβ* = − X
− K 2 V α* + K 1Vβ* = Z
− K 2 V α* − K1 Vβ* = −Y
K 2 V α* − K 1 Vβ* = −Z
(6)
−
3 2
V
2
Tab. 4.6 – Tempi di applicazione dei vettori attivi in funzione delle variabili X, Y e Z
dove si è posto:
K1 =
3 T
3 T
, K2 =
2 V dc
2 V dc
(4.24)
20
4 Tecniche di modulazione PWM
Nella figura seguente sono illustrati i pattern dei segnali di comando in ciascun sestante
rispetto alla portante triangolare. Le commutazioni dei comandi di ramo dell’inverter sono
ottenute dal confronto (“compare”) della portante con gli istanti di commutazione ta, tb, e tc
definiti come:
T0
T
T
, t b = 0 + T1 , t c = 0 + T1 + T2
2
2
2
ta =
(4.25)
Indicando con CMPR1, CMPR2 e CMPR3 i registri di comparazione che determinano la
commutazione rispettivamente del ramo 1 (segnale d1), 2 (d2) e 3 (d3), in base alla logica di
commutazione sarà necessario caricare, in ciascun sestante i registri con i tempi di
commutazione opportuni. Come è facile ricostruire dalla figura si ha:
sestante
CMPR1
CMPR2
CMPR3
(3)
ta
tb
tc
(1)
tb
ta
tc
(5)
tc
ta
tb
(4)
tc
tb
ta
(6)
tb
tc
ta
(2)
ta
tc
tb
Tab. 4.7 – Attribuzione dei tempi di commutazione nei diversi sestanti
(3)
CMPR3
CMPR2
CMPR1
(1)
CMPR3
CMPR1
CMPR2
d1
0
1
1
1
d1
0
0
1 1
d2
0
0
1 1
d2
0
1
1
d3
0
0
0 1
d3
0
0
0 1
tb tc
ta
tb tc
ta
(5)
CMPR1
CMPR3
CMPR2
1
(4)
CMPR1
CMPR2
CMPR3
d1
0
0
0 1
d1
0
0
d2
0
1
1
1
d2
0
0
1 1
d3
0
0
1 1
d3
0
1
1
tb tc
ta
(6)
CMPR3
1
tb tc
ta
CMPR2
CMPR1
0 1
(2)
CMPR2
CMPR3
CMPR1
d1
0
0
1 1
d1
0
1
1
d2
0
0
0 1
d2
0
0
0 1
d3
0
1
d3
0
1
ta
1
tb tc
0
ta
1
1 1
tb tc
Fig. 4.26 - Pattern dei segnali di comando di ramo nei diversi sestanti
Modulazione dei vettori di spazio (SV-PWM)
21
r
V3 (010)
r
V2 (110)
β
1
2
3
5
1
2
3
r
V4
(011)
1
2
3
3
1
2
3
1
1
2
3
6
4
r
V5 (001)
1
2
3
r
V6
r α
V1 (100)
2
(101)
Fig. 4.27 - Pattern dei segnali di comando di ramo rispetto l’esagono di tensioni
4.2.5
Saturazione dei pattern dello SV-PWM
Un argomento di una certa rilevanza nella pratica applicativa riguarda la modalità di
funzionamento in condizioni al limite di tensione dello SV-PWM, e conseguentemente dei
criteri di saturazione dei segnali di comando.
Al riguardo in Fig. 4.21 sono rappresentati i limiti di funzionamento più significativi
dell’inverter trifase in relazione all’esagono della tensione di uscita. In particolare sono
illustrati i limiti di funzionamento in zona lineare della modulazione seno-triangolo, e dello SVPWM6.
Per sua natura, la tecnica SV-PWM è in grado di sintetizzare vettori di tensione finché questi
sono contenuti nell’esagono della tensione di uscita dell’inverter trifase. Cioè, in altri termini,
l’esagono di tensione rappresenta il luogo dei vertici dei vettori di tensione massimi
sintetizzabili dall’inverter trifase (per questo si parla anche di esagono “limite” di tensione).
Infatti, si può dimostrare analiticamente [1] che l’esagono limite è il luogo dei punti
caratterizzati da tempo di applicazione del vettore nullo pari a zero ( T0 = 0 ), il che corrisponde
all’applicazione dei vettori attivi per tutto il periodo di PWM ( T1 + T2 = T ).
Di contro, per vettori esterni all’esagono limite l’algoritmo dello SV-PWM porta al calcolo di
tempi di applicazione dei vettori attivi la cui somma è maggiore del periodo di PWM
( T1 + T2 > T ).
In questo caso è possibile definire dei criteri di correzione dei tempi tali da soddisfare
determinate caratteristiche di funzionamento e garantire nel contempo il corretto pilotaggio
dell’unità di PWM.
Peraltro, se si vuole assicurare con lo SV-PWM una alimentazione (come media nel periodo)
di tipo sinusoidale, cioè vettori rotanti di ampiezza costante, sarà necessario restare nei limiti
del cerchio inscritto all’esagono di tensione, avente ampiezza pari a 1 / 3 = 0.577 .
6
Per campo di funzionamento lineare di una tecnica di modulazione si intende la zona nella quale la prima armonica della tensione
di uscita varia linearmente con l’ingresso di modulazione. Nel caso della modulazione seno-triangolo l’ingresso è rappresentato
dall’ampiezza della modulante; nello SV-PWM l’ingresso è l’ampiezza del vettore di riferimento.
La modulazione SV-PWM ha un campo di funzionamento lineare pari al massimo ottenibile con l’inverter, più esteso della
modulazione seno-triangolo a meno che in questa non si ricorra all’inserzione della terza armonica (cfr. Fig. 4.21 essendo
1 / 3 = 0.577 ).
22
4 Tecniche di modulazione PWM
b
β
SV-PWM
OL=2/3Vdc
OM = 1 / 3V dc
ON=1/2Vdc
M
O
N
L
α=a
S∆-PWM
c
Fig. 4.28 - Limiti in tensione dell’inverter trifase
Nel seguito sono presentate le tre modalità di funzionamento al limite di tensione più
comuni: la saturazione nel cerchio inscritto, la saturazione sull’esagono limite e la transizione
nel funzionamento a six-step.
4.2.6
Saturazione nel cerchio inscritto all’esagono di tensione
Questa modalità di saturazione viene messa in atto quando si vuole evitare che l’ampiezza
del vettore sintetizzato fuoriesca dal cerchio inscritto, cioè si vuole garantire un funzionamento
sempre “sinusoidale” dell’inverter. In tal caso si rinuncia a sfruttare completamente la capacità
dell’inverter ma si impedisce che la modulazione introduca una distorsione della tensione che,
di solito, è causa di instabilità negli azionamenti controllati in corrente.
La logica di saturazione è la seguente:
•
r
si calcola l’ampiezza del vettore di riferimento |V * |
•
si calcola il rapporto tra questo ed il limite di tensione δ =
r
|V * |
Vdc
3
•
se ξ>1 allora poni: T1,lim
(
T
T
= 1 ; T2,lim = 1 ; T0 ,lim = T − T1,lim + T2 ,lim
δ
δ
)
Questa saturazione conserva la direzione del vettore di tensione (data dal rapporto tra i
tempi di applicazione dei vettori attivi T1 / T2 ) e garantisce un tempo un tempo di applicazione
del vettore nullo T0 ≥ 0 (l’uguaglianza a zero si verifica solo in corrispondenza delle bisettrici
dei sestanti).
4.2.7
Saturazione sull’esagono limite di tensione
Questa modalità di saturazione è attivata quando si voglia sfruttare tutta la capacità di
sintesi vettoriale dell’inverter trifase e si sia in grado di accettare le distorsioni di tensione che
seguono all’applicazione di vettori esterni al cerchio inscritto. Un caso tipico è quello di
Modulazione dei vettori di spazio (SV-PWM)
23
azionamenti con controllo scalare azionati da inverter a pilotaggio mediante condensatori di
“bootstrap”7.
Una semplice logica di saturazione che mantiene la direzione del vettore di tensione è la
seguente:
T1 + T2
T
T1
T
=
; T2 ,lim = 1 ; T0,lim = 0
δ
δ
•
si calcola il rapporto tra i tempi δ =
•
se ξ>1 allora poni: T1,lim
Una semplice variante di questa logica è quella che prevede in ogni caso un tempo minimo
di applicazione del vettore nullo ( T0,min = costante > 0 ). Questo deve essere assicurato ad esempio
nel caso in cui sia prevista la misura della corrente mediante shunt resistivi posti in serie tra gli
switch inferiori dell’inverter e la linea negativa del bus in continua [2].
La condizione T0,min = costante inserita nella logica precedente porta alla saturazione su un
esagono interno all’esagono limite di tensione.
4.2.8
Transizione nel funzionamento a six-step
Questa modalità di saturazione consente di attingere il funzionamento a sei gradini
dell’inverter trifase, consentendo quindi di sfruttare tutta la capacità di tensione in termini di
valore efficace della tensione di uscita. Si ammette la distorsione della tensione (e quindi della
corrente) di uscita.
La logica di saturazione è la seguente:
•
si calcola la somma dei tempi di applicazione dei vettori non nulli δ = T1 + T2
•
se ξ>T allora esegui i controlli seguenti:
- se T1 > T2 allora poni T1,lim = T ; T2,lim = 0 ; T0 ,lim = 0
-
invece se T2 > T1 allora poni T2,lim = T ;
-
T1,lim = 0 ; T0,lim = 0
invece se T2 = T1 allora poni T1,lim = T / 2 ;
T2,lim = T / 2 ; T0,lim = 0
Tale logica sfocia nel comando a sei gradini nel caso l’ampiezza del vettore di riferimento
(supposta costante) sia maggiore del cerchio circoscritto all’esagono. Poiché nel comando a sei
gradini sono utilizzati solo i vettori attivi dell’inverter, ciascuno per un sesto del periodo della
fondamentale, il tempo minimo tra due commutazioni di ramo è proprio pari a tale valore.
Pertanto, tale modalità di funzionamento è applicabile agli azionamenti con controllo scalare
ma azionati da inverter in cui non è utilizzato il pilotaggio mediante condensatori di bootstrap.
4.2.9
Diagrammi delle grandezze nella modulazione SV-PWM
Nel seguito sono illustrati gli andamenti delle principali grandezze alle quali si è fatto
riferimento nella descrizione della modulazione SV-PWM. Tali andamenti sono stati ottenuti
7
In tali inverter il comando di ciascuno degli switch connessi alla linea positiva del bus in continua è fornito dalla carica
immagazzinata in condensatori, detti di “bootstrap”, i quali si caricano quando lo switch inferiore si chiude. Pertanto tali inverter,
per funzionare correttamente, hanno bisogno che ciascun ramo commuti sicuramente entro un certo tempo, progettato in modo
da essere superiore (ma non di molto) del periodo di PWM di funzionamento.
24
4 Tecniche di modulazione PWM
attraverso un programma di simulazione di azionamenti elettrici relativamente al comando di
un motore asincrono.
Gli andamenti da Fig. 4.29 a Fig. 4.33 descrivono il funzionamento quando l’ampiezza del
comando di tensione è interna al cerchio inscritto all’esagono della tensione di uscita
dell’inverter. In particolare, in Fig. 4.29 e Fig. 4.30 sono riportati gli andamenti delle componenti
“alfa” e “beta” della tensione di riferimento, effettiva e della corrente8.
Vα
Vα*
iα
ampiezza
riferimento di
tensione
0.75
frequenza
modulante
100 Hz
periodo PWM
200 us
tensione
sul bus DC
Vdc
= 0.577
3
“per unit”
tensione
1 = cerchio
inscritto
tipo
funzionamento
nel cerchio
inscritto
ampiezza
riferimento di
tensione
0.75
frequenza
modulante
100 Hz
periodo PWM
200 us
tensione
sul bus DC
Vdc
= 0.577
3
“per unit”
tensione
1 = cerchio
inscritto
tipo
funzionamento
nel cerchio
inscritto
Fig. 4.29 – Tensione e corrente “alfa”
Vβ
Vβ*
iβ
Fig. 4.30 – Tensione e corrente “beta”
In Fig. 4.31 sono ancora illustrate le componenti della corrente insieme ai valori ottenuti
campionando in uno dei punti di simmetria del pattern PWM (istanti centrali del tempo di
applicazione del vettore nullo, corrispondenti al vertice ed allo zero della portante triangolare,
cfr. Fig. 4.25).
8
In base alla trasformazione di fase utilizzata, si può osservare come la componente “alfa” corrisponde identicamente alla fase “a”
del sistema effettivo, quindi gli andamenti relativi a questa componente coincidono con quelli effettivamente misurabili sulle fasi del
sistema, mentre la componente “beta” è proporzionale alla differenza tra le grandezze “b” e “c” nel sistema reale, ed è quindi
rappresentativa delle grandezze reali di “linea” anche dette “concatenate”. Questo è evidente dal confronto con le Fig. 3.6
eErrore. L'origine riferimento non è stata trovata..
Modulazione dei vettori di spazio (SV-PWM)
25
Si può osservare come, in un controllo digitale, questa semplice sincronizzazione del
campionamento sia sufficiente ad effettuare una sorta di filtraggio delle forme d’onda di
corrente, consentendo di tagliare fuori le ondulazioni ad alta frequenza (“ripple”) introdotte
dalla modulazione ed ottenere il valore “medio-nel-periodo” di PWM della corrente, che
rappresenta ciò che realmente si può (e talora si deve) controllare in un azionamento a comando
PWM9.
iα
iα#
iβ
iβ#
ampiezza
riferimento di
tensione
0.75
frequenza
modulante
100 Hz
periodo PWM
200 us
tensione
sul bus DC
Vdc
= 0.577
3
“per unit”
tensione
1 = cerchio
inscritto
tipo
funzionamento
nel cerchio
inscritto
Fig. 4.31 – Correnti “alfa” e “beta” effettive e campionate nel punto di simmetria
In Fig. 4.32 è illustrato, per un solo morsetto, l’andamento della tensione di uscita
dell’inverter10 e il corrispondente valore “medio-nel-periodo” di PWM, in corrispondenza dei
sestanti dell’esagono della tensione, rappresentati con la codifica di Tab. 4.4. In Fig. 4.33 sono
invece illustrati gli andamenti delle tensioni “medie-nel-periodo” relativi a due cicli per i tre
morsetti di uscita.
Si puo osservare la tipica forma a doppia cupola molto simile a quella ottenibile dalla
modulazione S∆-PWM con inserzione di terza armonica descritta in Fig. 4.20. Questa
circostanza testimonia del fatto che, con la modulazione SV-PWM, al morsetto dell’inverter è, di
fatto, inserita in modo “automatico” una terza armonica che è quella che consente l’estensione
del campo lineare di funzionamento dell’inverter trifase come indicato in Fig. 4.21.
9
Con il comando PWM digitale si fa riferimento a grandezze che sono costanti nel periodo di modulazione. Tutte le variazioni
all’interno del periodo delle grandezze reali (sia che si tratti di ripple di corrente, che di chopperaggio delle tensioni) va
considerato come un rumore (paraltro inevitabile) del sistema.
10
Diversamente dalla convenzione adottata in Fig. 2.3, negli andamenti presentati in questo paragrafo si suppone che la tensione ai
morsetti di uscita dell’inverter sia misurata rispetto alla linea negativa del DC bus.
26
4 Tecniche di modulazione PWM
V1mα
V1m
sextant
ampiezza
riferimento di
tensione
0.75
frequenza
modulante
100 Hz
periodo PWM
200 us
tensione
sul bus DC
Vdc
= 0.577
3
“per unit”
tensione
1 = cerchio
inscritto
tipo
funzionamento
nel cerchio
inscritto
Fig. 4.32 – Tensione effettiva e “media-nel-periodo” al morsetto dell’inverter e sestante
V1mav
V3mav
V2mav
sextant
ampiezza
riferimento di
tensione
0.75
frequenza
modulante
100 Hz
periodo pwm
100 us
tensione
sul bus dc
Vdc
= 0.577
3
“per unit”
tensione
1 = cerchio
inscritto
tipo
funzionamento
nel cerchio
inscritto
Fig. 4.33 – Tensione “media-nel-periodo”ai morsetti dell’inverter e sestante
In Fig. 4.34 è illustrata la modalità di variazione dei tempi di applicazione dei vettori attivi e
nulli lungo i sestanti dell’esagono di tensione.
Si può osservare come il tempo di applicazione del vettore nullo abbia un minimo in
corrispondenza della bisettrice di ciascun sestante, punto in cui è minima la distanza
dall’esagono limite, mentre i vettori attivi assumano valore massimo e rispettivamente zero nel
passaggio da un sestante all’altro.
Modulazione dei vettori di spazio (SV-PWM)
27
ampiezza
riferimento di
tensione
0.75
frequenza
modulante
100 Hz
periodo PWM
200 us
T0
tensione
sul bus DC
Vdc
= 0.577
3
T2
“per unit”
tensione
1 = cerchio
inscritto
“per unit” tempi
1 = ½ TPWM
tipo
funzionamento
nel cerchio
inscritto
sextant
T1
Fig. 4.34 – Tempi di applicazione dei vettori attivi e nulli lungo i sestanti
In Fig. 4.35 sono illustrati gli stessi tempi nel caso di imposizione di un riferimento di
tensione di ampiezza pari al raggio del cerchio inscritto all’esagono limite di tensione. Rispetto
alla figura precedente si può notare come il tempo di applicazione del vettore nullo diventi pari
a zero in corrispondenza delle bisettrici dei sestanti, punto nel quale la somma dei tempi di
applicazione dei vettori attivi diventa uguale al semiperiodo di PWM (1 pu).
T1
T0
T2
sextant
ampiezza
riferimento di
tensione
1
frequenza
modulante
100 Hz
periodo pwm
100 us
tensione
sul bus dc
Vdc
= 0.577
3
“per unit”
tensione
1 = cerchio
inscritto
“per unit” tempi
1 = ½ TPWM
tipo
funzionamento
sul cerchio
inscritto
Fig. 4.35 – Tempi di applicazione dei vettori attivi e nulli lungo i sestanti
Negli andamenti da Fig. 4.36 fino a Fig. 4.38 è illustrato il caso in cui venga applicato un
riferimento di tensione di ampiezza pari al raggio del cerchio circoscritto all’esagono di
tensione, e venga applicata la modalità di saturazione del comando sull’esagono stesso descritta
al par. 0.
In Fig. 4.34 sono presentati gli andamenti del riferimento di tensione e della corrispondente
tensione “media nel periodo” in forma polare. Essi sono ottenuti componendo, rispettivamente
in ascissa ed ordinata, le componenti “alfa” e “beta” nel tempo. Nella successiva Fig. 4.37 le
componenti della tensione “media-nel-periodo” sono presentate nel tempo e rispetto al sestante.
28
4 Tecniche di modulazione PWM
Vβ*
Vβav
Vα*
Vαav
ampiezza
riferimento di
tensione
1.156
frequenza
modulante
100 Hz
periodo PWM
100 us
tensione
sul bus DC
Vdc
= 0.577
3
“per unit”
tensione
1 = cerchio
inscritto
tipo
funzionamento
sul cerchio
circoscritto
Fig. 4.36 – Tensioni “alfa-beta” di comando e “medie-nel-periodo” in forma polare
Vαav
Vβav
sextant
ampiezza
riferimento di
tensione
1.156
frequenza
modulante
100 Hz
periodo pwm
100 us
tensione
sul bus dc
Vdc
= 0.577
3
“per unit”
tensione
1 = cerchio
inscritto
tipo
funzionamento
sul cerchio
circoscritto
Fig. 4.37 – Tensioni “alfa-beta” “medie-nel-periodo” lungo i sestanti
In Fig. 4.38 è riportato l’andamento delle tensioni “alfa-beta” effettive e delle omologhe
correnti, queste ultime presentate in forma polare in Fig. 4.3911.
Questi andamenti consentono di valutare la distorsione di corrente causata dalla saturazione
delle tensioni, peraltro trascurabile in forma polare. Consente anche di comprendere le
caratteristiche del ripple di corrente dovuto alla modulazione. Si possono notare, infatti, sei
zone in cui il ripple è più elevato. Considerando lo sfasamento di circa π/2 esistente, nel caso
considerato, tra tensione e corrente, ne risulta che l’ondulazione di corrente è massima quando
il riferimento di tensione è allineato con le bisettrici dei sestanti, laddove sono entrambi
massimi i tempi di applicazione dei vettori attivi, mentre è minimo il tempo di applicazione del
vettore nullo12.
11
È possibile osservare la costanza della tensione beta in corrispondenza dei settori 1 e 6, il che non vuol dire assenza di
commutazioni, ma solo che si sta commutando tra vettori di spazio aventi la stessa compoonente.
12
Si ricordi che vettore nullo vuol dire fase di ricircolo nei diodi dell’inverter, la corrente tende a zero spinta dalla tensione
indotta nelle fasi del motore; vettore attivo vuol dire invece fase di alimentazione attraverso i transistors, la corrente è forzata a
variare dalla differenza tra la tensione applicata e quella indotta nelle fasi.
Modulazione dei vettori di spazio (SV-PWM)
29
Vα
ampiezza
riferimento di
tensione
1.156
Vβ
frequenza
modulante
100 Hz
periodo pwm
100 us
tensione
sul bus dc
Vdc
= 0.577
3
“per unit”
tensione
1 = cerchio
inscritto
tipo
funzionamento
sul cerchio
circoscritto
iα
iβ
Fig. 4.38 – Tensioni e correnti “alfa-beta”
iβ*
iα*
ampiezza
riferimento di
tensione
1.156
frequenza
modulante
100 Hz
periodo PWM
100 us
tensione
sul bus DC
Vdc
= 0.577
3
“per unit”
tensione
1 = cerchio
inscritto
tipo
funzionamento
Sul cerchio
circoscritto
Fig. 4.39 – Correnti “alfa-beta” in forma polare
V1mav
V2mav
V3mav
sextant
ampiezza
riferimento di
tensione
1.156
frequenza
modulante
100 Hz
periodo PWM
100 us
tensione
sul bus DC
Vdc
= 0.577
3
“per unit”
tensione
1 = cerchio
inscritto
tipo
funzionamento
sul cerchio
circoscritto
Fig. 4.40 – Tensioni “medie-nel-periodo” ai morsetti dell’inverter lungo i sestanti
30
4 Tecniche di modulazione PWM
In Fig. 4.41 sono illustrati i tempi di applicazione dei vettori dello SV-PWM. Si può verificare
il tempo di applicazione del vettore nullo costantemente a zero, mentre i tempi di applicazione
dei vettori attivi variano in modo lineare lungo il settore riempiendo l’inetro semiperiodo do
PWM.
T1
sextant
T2
T0
ampiezza
riferimento di
tensione
1.156
frequenza
modulante
100 Hz
periodo PWM
100 us
tensione
sul bus DC
Vdc
= 0.577
3
“per unit”
tensione
1 = cerchio
inscritto
“per unit” tempi
1 = ½ TPWM
tipo
funzionamento
sul cerchio
circoscritto
Fig. 4.41 – Tempi di applicazione dei vettori attivi e nulli lungo i sestanti
Le curve in Fig. 4.42 fino alla Fig. 4.46 mostrano infine il caso in cui il riferimento di tensione
assume una ampiezza intermedia tra il raggio del cerchio inscritto e circoscritto, sempre nel
caso in cui si ponga in atto la saturazione sull’esagono limite di tensione.
Vβ*
Vβav
Vα*
Vαav
ampiezza
riferimento di
tensione
1.078
frequenza
modulante
100 Hz
periodo PWM
100 us
tensione
sul bus DC
Vdc
= 0.577
3
“per unit”
tensione
1 = cerchio
inscritto
tipo
funzionamento
tra il cerchio
inscritto ed il
circoscritto
Fig. 4.42 – Tensioni “alfa-beta” di comando e “medie-nel-periodo” in forma polare
Modulazione dei vettori di spazio (SV-PWM)
Vαav
sextant
Vβav
31
ampiezza
riferimento di
tensione
1.078
frequenza
modulante
100 Hz
periodo PWM
100 us
tensione
sul bus DC
Vdc
= 0.577
3
“per unit”
tensione
1 = cerchio
inscritto
tipo
funzionamento
tra il cerchio
inscritto ed il
circoscritto
Fig. 4.43 – Tensioni “alfa-beta” “medie-nel-periodo” lungo i sestanti
T1
sextant
T0
T2
ampiezza
riferimento di
tensione
1.078
frequenza
modulante
100 Hz
periodo PWM
100 us
tensione
sul bus DC
Vdc
= 0.577
3
“per unit”
tensione
1 = cerchio
inscritto
“per unit” tempi
1 = ½ TPWM
tipo
funzionamento
tra il cerchio
inscritto ed il
circoscritto
Fig. 4.44 – Tempi di applicazione dei vettori attivi e nulli lungo i sestanti
V1mav
V2mav
V3mav
sextant
ampiezza
riferimento di
tensione
1.078
frequenza
modulante
100 Hz
periodo PWM
100 us
tensione
sul bus DC
Vdc
= 0.577
3
“per unit”
tensione
1 = cerchio
inscritto
tipo
funzionamento
tra il cerchio
inscritto ed il
circoscritto
Fig. 4.45 – Tensioni “medie-nel-periodo”ai morsetti dell’inverter lungo i sestanti
32
4 Tecniche di modulazione PWM
V1mα
sextant
V1m
ampiezza
riferimento di
tensione
1.078
frequenza
modulante
100 Hz
periodo PWM
100 us
tensione
sul bus DC
Vdc
= 0.577
3
“per unit”
tensione
1 = cerchio
inscritto
tipo
funzionamento
tra il cerchio
inscritto ed il
circoscritto
Fig. 4.46 – Tensione al morsetto dell’inverter e “media-nel-periodo” lungo i sestanti
Bibliografia
[1] L. Egidi “Modulatore digitale per il comando di un inverter a tensione impressa secondo la tecnica
dei vettori di spazio”, Tesi di Laurea della Facoltà di Ingegneria dell’Università dell’Aquila, a.a.
1992/93.
[2] R. Petrella, F. Parasiliti, M. Tursini “Low Cost Phase Current Sensing in DSP Based AC Drives”,
Proc. of the IEEE International Symposium on Industrial Electronics, (ISIE’99), p.1284-1289, Bled
(Slovenia), 12-16 luglio 1999.
Test di apprendimento
Indice delle figure e delle tabelle
Fig. 1.1 - Schema dell'inverter trifase ............................................................................................................................. 1
Fig. 1.2 – Comando di ramo.......................................................................................................................................... 1
Fig. 2.3 - Tensioni di uscita dell’inverter trifase ............................................................................................................. 2
Fig. 2.4 - Stati dell’inverter trifase .................................................................................................................................. 3
Fig. 3.5 - Tensioni di uscita riferite al punto centrale del bus DC................................................................................. 4
Fig. 3.6 - Tensioni di uscita concatenate ........................................................................................................................ 4
Fig. 3.7 – Stati dell’inverter e tensioni ai morsetti nel comando “six-step” .................................................................... 7
Fig. 3.8 – Stati dell’inverter e tensioni sul carico nel comando “six- step” ..................................................................... 7
Fig. 3.9 - Esagono delle tensioni di uscita dell’inverter trifase ........................................................................................ 8
Fig. 4.10 – Modulazione S∆-PWM................................................................................................................................ 9
Fig. 4.11 - Portante e modulante nella S∆-PWM con p = 12, M = 0.6 ........................................................................ 9
Fig. 4.12 - Tensione di uscita (fase a) riferita al punto centrale del bus DC. ................................................................ 10
Fig. 4.13 - Tensione concatenata ................................................................................................................................. 10
Fig. 4.14 - Tipico spettro della modulazione S∆-PWM (M = 0.8) ............................................................................. 11
Fig. 4.15 - Ampiezza relativa delle armoniche in funzione dell'indice di modulazione (tensione di uscita dell’inverter
riferita al centrale del bus DC)................................................................................................................ 11
Fig. 4.16 - S∆-PWM con p = 12, M = 1.1 ................................................................................................................... 12
Fig. 4.17 - S∆-PWM con p = 12, M = 5 ...................................................................................................................... 12
Fig. 4.18 - Ampiezza della 1a armonica della tensione concatenata in funzione dell'indice di modulazione (p = 15) .. 12
INDICE
33
Fig. 4.19 - Andamento reale delle tensioni armoniche in funzione dell'indice di modulazione, in presenza del circuito
di lockout ................................................................................................................................................ 13
Fig. 4.20 - S∆-PWM con p = 12, M = 1.1: terza armonica nella tensione di riferimento........................................... 14
Fig. 4.21 - Ampiezza della 1a armonica della tensione di fase (collegamento a stella del carico in funzione dell’indice
di modulazione ( p = 15 )........................................................................................................................ 14
Fig. 4.22 - Sintesi del vettore di tensione nello SV-PWM ............................................................................................ 15
Fig. 4.23 - Relazione tra le componenti xyz ed i settori angolari ................................................................................. 16
Fig. 4.24 - Codifica dei sestanti ................................................................................................................................... 17
Fig. 4.25 - SV-PWM simmetrico.................................................................................................................................. 18
Fig. 4.26 - Pattern dei segnali di comando di ramo nei diversi sestanti ........................................................................ 20
Fig. 4.27 - Pattern dei segnali di comando di ramo rispetto l’esagono di tensioni........................................................ 21
Fig. 4.28 - Limiti in tensione dell’inverter trifase.......................................................................................................... 22
Fig. 4.29 – Tensione e corrente “alfa” ......................................................................................................................... 24
Fig. 4.30 – Tensione e corrente “beta” ........................................................................................................................ 24
Fig. 4.31 – Correnti “alfa” e “beta” effettive e campionate nel punto di simmetria..................................................... 25
Fig. 4.32 – Tensione effettiva e “media-nel-periodo” al morsetto dell’inverter e sestante............................................ 26
Fig. 4.33 – Tensione “media-nel-periodo”ai morsetti dell’inverter e sestante .............................................................. 26
Fig. 4.34 – Tempi di applicazione dei vettori attivi e nulli lungo i sestanti................................................................... 27
Fig. 4.35 – Tempi di applicazione dei vettori attivi e nulli lungo i sestanti................................................................... 27
Fig. 4.36 – Tensioni “alfa-beta” di comando e “medie-nel-periodo” in forma polare ................................................. 28
Fig. 4.37 – Tensioni “alfa-beta” “medie-nel-periodo” lungo i sestanti......................................................................... 28
Fig. 4.38 – Tensioni e correnti “alfa-beta”................................................................................................................... 29
Fig. 4.39 – Correnti “alfa-beta” in forma polare.......................................................................................................... 29
Fig. 4.40 – Tensioni “medie-nel-periodo” ai morsetti dell’inverter lungo i sestanti ..................................................... 29
Fig. 4.41 – Tempi di applicazione dei vettori attivi e nulli lungo i sestanti................................................................... 30
Fig. 4.42 – Tensioni “alfa-beta” di comando e “medie-nel-periodo” in forma polare ................................................. 30
Fig. 4.43 – Tensioni “alfa-beta” “medie-nel-periodo” lungo i sestanti......................................................................... 31
Fig. 4.44 – Tempi di applicazione dei vettori attivi e nulli lungo i sestanti................................................................... 31
Fig. 4.45 – Tensioni “medie-nel-periodo”ai morsetti dell’inverter lungo i sestanti ...................................................... 31
Fig. 4.46 – Tensione al morsetto dell’inverter e “media-nel-periodo” lungo i sestanti................................................. 32
Tab. 2.1 – Stati e rispettivi comandi di ramo................................................................................................................. 3
Tab. 3.2 – Stati, comandi di ramo e vettori di spazio ................................................................................................... 8
Tab. 4.3 – Sestanti in funzione delle componenti xyz.................................................................................................. 16
Tab. 4.4 – Codifica dei sestanti in funzione delle componenti xyz .............................................................................. 17
Tab. 4.5 – Tempi di applicazione dei vettori di spazio nei diversi sestanti .................................................................. 19
Tab. 4.6 – Tempi di applicazione dei vettori attivi in funzione delle variabili X, Y e Z ........................................... 19
Tab. 4.7 – Attribuzione dei tempi di commutazione nei diversi sestanti...................................................................... 20
INDICE
TECNICHE DI PILOTAGGIO DELL’INVERTER TRIFASE........................................1
1
Nozioni di base ..........................................................................................................1
2
Calcolo delle tensioni di uscita ................................................................................1
3
Comando ad onda quadra (Six Step) ......................................................................4
3.1
Scomposizione in serie di Fourier................................................................................ 5
3.1.1
3.1.2
3.1.3
3.1.4
3.2
4
4.1
Tensioni di uscita riferite al punto centrale del bus DC ........................................................5
Tensioni di uscita concatenate ..............................................................................................5
Tensione del centro stella del carico riferita al punto centrale del bus DC............................5
Tensioni di fase del carico .....................................................................................................6
Rappresentazione vettoriale della tensione di uscita ................................................. 7
Tecniche di modulazione PWM ..............................................................................8
Modulazione seno-triangolo (S∆-PWM) ...................................................................... 8
34
4.1.1
4.1.2
4.1.3
4.2
4.2.1
4.2.2
4.2.3
4.2.4
4.2.5
4.2.6
4.2.7
4.2.8
4.2.9
4 Tecniche di modulazione PWM
Scomposizione in serie di Fourier ....................................................................................... 10
Sovra-modulazione ( M > 1 ) .............................................................................................. 12
Distorsione della modulante ............................................................................................... 13
Modulazione dei vettori di spazio (SV-PWM) ...........................................................14
Introduzione ....................................................................................................................... 14
Calcolo del settore angolare................................................................................................ 15
Sintesi del vettore di tensione.............................................................................................. 17
SV-PWM simmetrico ......................................................................................................... 18
Saturazione dei pattern dello SV-PWM ............................................................................. 21
Saturazione nel cerchio inscritto all’esagono di tensione .................................................... 22
Saturazione sull’esagono limite di tensione ......................................................................... 22
Transizione nel funzionamento a six-step........................................................................... 23
Diagrammi delle grandezze nella modulazione SV-PWM ................................................. 23
Bibliografia ..................................................................................................................................32
Test di apprendimento ..............................................................................................................32
Indice delle figure e delle tabelle...............................................................................................32
INDICE ........................................................................................................................................33