Teoremi sui triangoli rettangoli
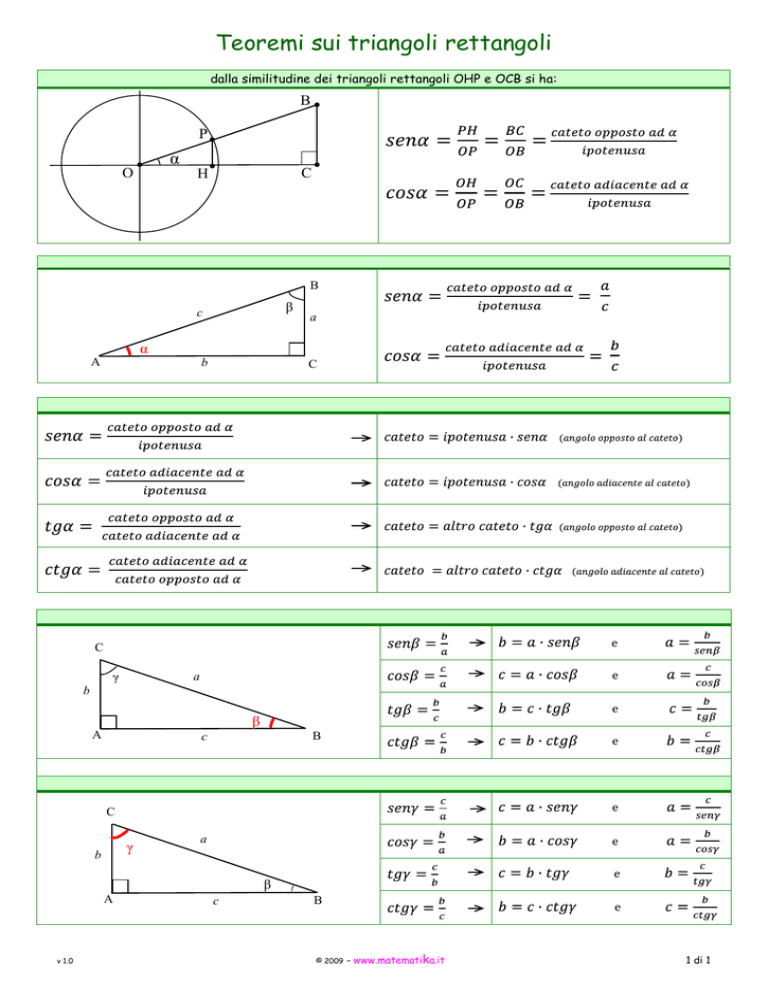
dalla similitudine dei triangoli rettangoli OHP e OCB si ha:
B
P
α
O
C
H
B
β
c
a
α
A
b
C
e
C
γ
e
a
b
e
β
A
B
c
e
e
C
γ
b
e
a
e
β
A
v 1.0
c
B
© 2009
e
- www.matematika.it
1 di 1
Teoremi sui triangoli qualsiasi
teorema della corda
B
la misura di una corda è uguale al prodotto del diametro per il
seno di uno degli angoli alla circonferenza che insistono sulla
corda:
β
r
A
α
teorema dei seni o di Eulero
in un triangolo il rapporto tra la misura di un lato e il seno
dell’angolo opposto è costante:
C
γ
b
a
α
β
A
oppure
B
c
corollari
C
per il teorema della corda, detto r il raggio della circonferenza
circoscritta al triangolo, il rapporto tra un lato e il seno dell’angolo
opposto è uguale a 2r:
γ
r
β
α
B
A
teorema delle proiezioni
in un triangolo la misura di un lato è uguale alla somma dei
prodotti di quelle degli altri due lati per il coseno dell’angolo
che ciascuno di questi forma con il primo:
C
b
a
γ
α
A
β
H c
B
teorema del coseno o di Carnot
in un triangolo il quadrato della misura di un lato è uguale alla
somma dei quadrati delle misure degli altri due lati, meno il
doppio prodotto delle misure di questi due lati per il coseno
dell’angolo tra essi compreso:
C
b
a
γ
β
α
A
c
B
area di un triangolo
C
b
a
γ
α
A
v 1.1
L’area di un triangolo è uguale al semiprodotto di due lati per il
seno dell’angolo tra essi compreso
β
c
B
© 2009
- www.matematika.it
1 di 1
Formule di Trigonometria
formule di Briggs
C
b
dato un triangolo qualsiasi di cui siano note le misure dei
lati e il semiperimetro p, i seni delle semiampiezze degli
angoli sono espresse dalle seguenti relazioni:
a
γ
α
β
A
c
B
formula di Erone
C
b
A
l’area di un triangolo qualsiasi si esprime in funzione del
semiperimetro p come:
a
B
c
teorema delle tangenti o di Nepero
C
a
b
α
A
β
c
B
applicazioni della trigonometria alla geometria analitica
significato trigonometrico del
angolare m di una retta y=mx+q
P2
α
P1
coefficiente
α
r
α
v 1.2
s
© 2009
tangente dell’angolo formato da due rette r ed
s di coefficiente angolare mr ed ms
- www.matematika.it
1 di 2
Formule di Trigonometria
applicazioni della trigonometria alla geometria
raggio della circonferenza circoscritta ad un
triangolo
C
γ
b
A
a
R
α
O
β
c
oppure
B
raggio della circonferenza inscritta in un
triangolo
C
γ
b
a
r
α
A
= area
β
B
c
oppure
= area p = semiperimetro
raggio della circonferenze ex-inscritte
(cioè tangente a un suo lato e ai prolungamenti degli altri due)
oppure
ra
C
oppure
γ
b
a
α
oppure
β
A
= area p = semiperimetro
B
c
mediane di un triangolo
C
b
α
A
a
γ
M
β
ma
B
c
bisettrici di un triangolo
C
γ
b
ba
α/2
A
D
a
β
B
c
area di un parallelogramma
area di un quadrilatero
D
C
C
D
b
A
v 1.2
α
a
A
B
α
d1
d2
B
© 2009
- www.matematika.it
2 di 2












