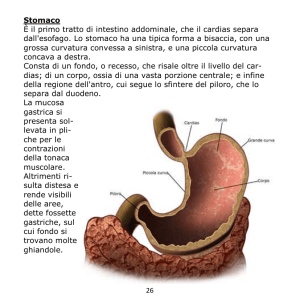
La gravità (secondo Tullio Regge)
La gravità non è una forza come
le altre: Einstein interpreta gli
effetti gravitazionali osservati
-tra corpi dotati di massacome indotti dalla curvatura di un
continuum quadridimensionale,
lo spazio-tempo
Annalisa Marzuoli
Dipartimento di Matematica
Università di Pavia
Grugliasco,7 aprile 2017
Nella Relatività Speciale
(Einstein 1905) erano stati già
‘unificati’ spazio e tempo nello
spazio-tempo di Minkowski,
la cui curvatura è nulla
1
I successi della teoria:
• modelli cosmologici,big bang
• precessione del perielio di
Mercurio
• deviazione dei raggi luminosi
• buchi neri (astrofisici e
galattici)
• prima rivelazione diretta di
onde gravitazionali (2016)
I problemi aperti
sono essenzialmente connessi alle
difficoltà di conciliare la teoria
classica di Einstein con la fisica
quantistica (supergravità,
II parte della conferenza → )
2
Equazioni di Einstein
della Relatività Generale:
curvatura
contenuto di massa-energia
[formalismo tensoriale,
covarianza generale,
principi variazionali,
geometrie riemanniane
(non euclidee)…]
3
I molteplici tipi di sorgenti
del campo gravitazionale
che si possono studiare
entrano nelle equazioni
di Einstein tramite il
tensore energia-impulso
Tik
Deep Sky map
(Hubble telescope)
Termini di curvatura nelle equazioni di Einstein
Rik – ½ R gik
(da ora in avanti)
4
La curvatura è percepibile attraverso l’ immersione di una
superficie generica S nello spazio fisico a 3 dimensioni.
Guardando regioni diverse emergono tre tipologie di
‘geometrie modello’, distinguibili per il segno della
curvatura di Gauss
La superficie di
una ‘sella’ (curvatura
di Gauss negativa)
La superficie di
una sfera
(curvatura di
Gauss positiva)
Il piano euclideo
è piatto, cioè ha
curvatura nulla
5
Curvatura di Gauss & theorema egregium
Definizione: in ogni punto p della superficie S la curvatura di Gauss è il
prodotto delle due ‘curvature principali’ (ciascuna uguale all’inverso del
raggio del cerchio osculatore) (*)
K (p) = K1 (p) K2 (p) = (1/R1) (1/R2) (p)
Teorema: la curvatura gaussiana di una superficie S dipende solo da una
quantità intrinseca, la prima forma fondamentale o tensore metrico g
di S, e dalle sue derivate prime e seconde.
La curvatura di Gauss totale per
una superficie S è una quantità
adimensionale.
Per una sfera di raggio r vale
Area / r ² = 4π ,
non dipende dal raggio ed è positiva.
(*) (Materiale di approfondimento su
6
questa parte: in fondo alle trasparenze)
Geometrie di Riemann (‘non euclidee’)
Il messaggio contenuto nel teorema di Gauss, cioé
le grandezze geometriche (lunghezze, aree, curvatura) sono definibili e
calcolabili senza ricorrere all’ uso di ‘arene esterne’
è la base delle generalizzazioni a spazi (e spazi-tempo) di dimensione n > 2
Le varietà riemanniane n-dimensionali sono spazi dotati di una metrica intrinseca
(tensore metrico) g la cui conoscenza permette di calcolare:
• le distanze tra punti lungo curve geodetiche (cioè di minima lunghezza)
• la curvatura in ogni punto e la curvatura totale.
Controparte della curvatura gaussiana K per le varietà riemanniane: curvature
sezionali, a loro volta derivabili dal tensore di Riemann.
Da quest’ ultimo, e dal tensore metrico g, si costruisce il termine geometrico delle
equazioni di Einstein ( Rik – ½ R gik )
I ‘gradi di libertà’ del campo gravitazionale sono contenuti nel tensore
metrico g di uno spazio-tempo 4-dimensionale (pseudo-riemanniano,
con segnatura lorentziana)
7
Queste curvature gaussiane e di Riemann sono
così complicate da definire e da calcolare in pratica…
C’ è un modo di visualizzare e calcolare la curvatura
che sia al contempo semplice e ‘intrinseco’?
Strada promettente: rinunciare alla
descrizione di geometrie ‘lisce’ (continue)
per passare a oggetti che ne costituiscano
discretizzazioni o ‘approssimazioni’, ma
senza perdere informazioni essenziali
Tullio Regge
8
La Relatività Generale senza Coordinate
Il Nuovo Cimento Vol XIX (1961) pp 558-571
D. Hilbert &
S. Cohn-Vossen
Anschauliche
Geometrie
1932
Traduzione inglese
Amer. Math.Soc.
Geometry and the
Imagination
1952 (→ 1999)
I edizione italiana
Geometria Intuitiva
1972,
con appendice di
Aleksandrov
I primi fondamenti
della topologia
(Ristampato nel 2016)
9
Il Regge Calculus [così è intitolato il capitolo scritto da
J A Wheeler, coautore del volume “Gravitation” (1973) ]
A. E’ una procedura di discretizzazione degli spazi (o anche degli
spazi-tempo): una varietà riemanniana n-dimensionale viene
rimpiazzata da una collezione di blocchi n-dimensionali, all’
interno dei quali la geometria è quella euclidea, cioè la metrica
è piatta
B. La geometria di un tale ‘scheletro’ deve essere completamente
caratterizzata, in modo intrinseco, assegnando:
o la collezione delle lunghezze (euclidee) dei lati dei blocchi
o le regole di incollamento dei blocchi tra di loro
C. La curvatura risulta essere concentrata in sotto-blocchi di
dimensione (n-2) chiamati cardini (o ‘ossa’ dello scheletro)
10
Negli spazi (o reticoli) di Regge
i blocchi costitutivi sono di forma triangolare (simplessi)
O-simplessi (vertici)
1-simplessi (lati)
2-simplessi (triangoli)
3-simplessi (tetraedri solidi)
(4-simplessi, ecc.)
al fine di ottenere dissezioni rigide, non deformabili (punto B.)
vedi → blocchi 3D a confronto: tetraedro e cubo.
Di conseguenza la geometria dei reticoli di Regge è
determinata dalla collezione delle lunghezze dei suoi lati,
senza dover specificare indipendentemente degli angoli
11
12
Nei reticoli di Regge
i blocchi simpliciali non sono in generale equilateri:
si adattano a modellare geometrie complicate
NB. La collezione delle lunghezze dei lati gioca il ruolo del
tensore metrico g che contiene (nel caso lorentziano) i gradi
di libertà del campo gravitazionale
→ si può quindi parlare di RETICOLI ‘DINAMICI’
13
Il Regge Calculus
non fornisce direttamente l’ analogo delle equazioni di Einstein
•
La quantità fondamentale è l’ azione di Regge IR, che in
sostanza rappresenta la curvatura totale del reticolo
espressa in termini delle lunghezze dei lati e di angoli:
questi ultimi sono calcolati a partire dalle lunghezze stesse
con formule della geometria euclidea ricordando il punto A.
•
Vediamo come si costruisce l’ azione di Regge, e di
conseguenza cosa significa l’ affermazione precedente:
C. La curvatura risulta essere concentrata in sotto-blocchi di
dimensione (n-2), i cardini
14
Azione di Regge per reticoli 2D
BLOCCHI: triangoli (2-simplessi euclidei)
CARDINI: vertici (0-simplessi) : v
IR (v) = ε (v) = 2 π – Σtri αtri
IR (reticolo 2D) = Σv ε (v)
ε (v): angolo di deficit
del vertice v; α è
l’ angolo formato dai
due lati del triangolo
‘tri’ che si incontrano
nel vertice v (calcolo
di geometria piana)
Il simbolo Σ indica la sommatoria
15
Es.) calcolo della azione di Regge per la superficie del
tetraedro regolare (bordo del tetraedro solido)
In ogni vertice v concorrono 3 triangoli equilateri
IR (v) = ε (v) = 2 π – Σtri αtri
= 2π – 3 (π/3) = π
IR (tetraedro) = Σv ε (v) = 4π
(valore della curvatura gaussiana della superficie della sfera)
16
Azione di Regge per reticoli 2D (continua)
IR (v) = ε (v) = 2 π – Σtri αtri
ε (v), l’ angolo di deficit del vertice v, può essere positivo
(esempio precedente), nullo o negativo
Nel vertice centrale i triangoli
si affollano: la somma dei loro angoli
al vertice è > 2 π e quindi ε (v) < 0
Porzione di piano
tessellata con triangoli
equilateri: ε (v) = 0
17
(Cupole semisferiche triangolate): la curvatura di
Regge dei vertici è positiva oppure nulla
18
Nella superficie triangolata (lati di lunghezze diverse) i vertici
hanno curvatura di Regge differenziata, e di segno positivo,
(nullo) e negativo. È quindi una rappresentazione di un reticolo
bidimensionale “generico”, così come era “generica” la
superficie usata per illustrare la geometria secondo Gauss
19
Azione di Regge per reticoli 3D
BLOCCHI: tetraedri solidi (3-simplessi euclidei)
CARDINI: lati (1-simplessi) : ɩ
ε (ɩ) = 2 π – Σtetra βtetra
IR (reticolo 3D) = Σɩ ε (ɩ) |ɩ|
In 3D l’ azione di Regge è dunque la somma degli angoli di
deficit, attribuiti ai lati, ‘pesati’ con la rispettiva lunghezza.
|ɩ| è la lunghezza del lato ɩ
ε (ɩ) è l’ angolo di deficit del lato ɩ ; β è l’ angolo diedrale
racchiuso dai due triangoli nel tetraedro ‘tetra’ che si
incontrano nel lato ɩ (calcolo di geometria solida)
20
Un esempio: non si può dissezionare lo spazio 3D
in tetraedri (solidi) regolari senza lasciare ‘vuoti’
Il lato centrale, in secondo piano, è condiviso da 4 tetraedri;
un quinto tetraedro potrebbe essere aggiunto, ma non
arriverebbe a ‘chiudere’ la configurazione (lato grigio).
Ogni lato condiviso da 5 tetraedri regolari ha deficit ε>0
21
Azione di Regge per reticoli 4D
BLOCCHI: 4-simplessi euclidei
CARDINI: triangoli (2-simplessi) : T
ε (T) = 2 π – Σ4sim θ4sim
IR (reticolo 4D) = ΣT ε (T) Area( T )
In 4D l’ azione di Regge è la somma degli angoli di deficit,
attribuiti ai triangoli T, ‘pesati’ con l’ area del rispettivo
triangolo, Area(T) (esprimibile in termini dei quadrati dei
suoi lati, cfr. la formula di Erone)
ε (T) è l’ angolo di deficit del triangolo T; θ è l’ angolo
(iperdiedrale) formato dai due tetraedri del 4-simplesso
‘4sim’ che si incontrano nel triangolo T
22
Cos’è un quadrisimplesso
Politopo in 4 dimensioni, analogo del tetraedro in 3D
← ← Dal suo grafo si riconoscono:
5 vertici (0-simplessi)
10 lati (1-simplessi)
10 facce triangolari (2-simplessi)
5 tetraedri (3-simplessi)
Realizzazione geometrica:
prendere un tetraedro, aggiungere
un vertice ‘nella quarta dimensione’,
congiungere il quinto vertice con
quelli originari generando così gli
altri 4 tetraedri
23
Domande frequenti sul Regge Calculus
•
•
•
Perché usare triangoli, tetraedri, ecc. e non altri tipi di
blocchi elementari? (a questo spero di aver già risposto)
E’ possibile formalizzare il ‘passaggio’ da reticoli di Regge a
varietà riemanniane (lisce), cioè qualche sorta di limite
continuo? Sì (sotto certe condizioni): l’azione di Regge 4D quando le lunghezze diventano sempre più piccole- diventa
l’ azione di Hilbert-Einstein della Relatività Generale
Esistono le equazioni di Regge, l’ analogo delle equazioni
di Einstein? Sì, ricavate nel lavoro del 1961 con un
procedimento variazionale a partire dalla azione di Regge.
Grazie per l’ attenzione. Ci sono altre domande?
24
25
Materiale supplementare: geometria delle
superficie e cenni di geometria riemanniana
26
Curvature principali: definite per mezzo delle proprietà
‘estrinseche’ della superficie, cioè dal modo in cui questa
appare (ri)piegata nello spazio ambiente euclideo
Costruzione: in ogni punto si
introduce il piano tangente e il
vettore normale alla superficie
in quel punto.
I piani normali, intersecati con
la superficie, individuano delle
linee curve. Utilizzando
la nozione di cerchio osculatore
si misura la curvatura di tali
curve. Casi:
• > 0 e uguale a 1/r
• < 0 e uguale a -1/r
• =0
r: raggio del cerchio osculatore
27
(Teorema) ci sono 2 direzioni principali distinte e ortogonali tra
loro in ogni punto di una superficie immersa nello spazio,
oppure tutte le direzioni sono principali
Curvature
principali
(in modulo)
Superficie della sella:
Curvature principali di segno diverso
K1 = + 1/r1 K2 = - 1/r2
K1 = 1/r1
K2 = 1/r2
(r1, r2 : raggi dei
cerchi osculatori)
Piano: caso limite
della sfera per
r → ∞ (K1 = K2 = 0)
Sfera di raggio r:
K1 = K2 = 1/r > 0
Curvature
principali uguali
tra loro e pari a
1/r in ogni punto
28
Curvatura di Gauss & theorema egregium
Definizione: in ogni punto p della superficie S la curvatura di
Gauss è il prodotto delle curvature principali in quel punto:
K (p) = K1 (p) K2 (p) [dimensioni: 1/area]
Teorema: la curvatura gaussiana di una superficie S dipende
solo da una quantità intrinseca, la prima forma fondamentale
o metrica di S, e dalle sue derivate prime e seconde.
La curvatura gaussiana totale della superficie S (compatta) è data dall’
integrale esteso a S della curvatura K(p)
K (S) = ∫ K(p) dσ
dσ è l’ elemento infinitesimo di area espresso, e.g., in opportune coordinate
parametriche (u,v), e inoltre K(p)=K(u,v) dipende in modo regolare dal posto
29
Esercizio: calcolo della curvatura gaussiana totale di una
sfera S di raggio r
•
•
•
Non serve ricordare cos’ è una sfera (luogo dei punti nello spazio
euclideo tridimensionale (x,y,z) tali che il quadrato della loro distanza dall’
origine sia pari al quadrato del raggio)
La sfera ha due (qualsiasi) curvature principali uguali tra loro ( = 1/r )
La curvatura gaussiana è il prodotto di due curvature principali
K (p) = (1/r ) (1/r ) in ogni p che giace su S
Nella formula generale K (S) = ∫ K(p) dσ :
o K(p) esce dall’ integrale poiché è costante: K (S) = K ∫ dσ
o l’ area della sfera, ∫ dσ, vale: 4π x (quadrato del raggio r)
Segue che K (S) = 4π (non dipende da r)
30
Conseguenze per lo studio della geometria delle superficie
e prospettiva sulle geometrie di Riemann
• L’ integrale della curvatura gaussiana è un invariante topologico per le
superficie (connesse, compatte, orientabili), cioè è indipendente da
dettagli quali lunghezza, estensione ecc.
• Quindi, per la sfera, non dipende dal raggio r. Questo si formalizza
attraverso la formula di Gauss-Bonnet (la sfera S non ha buchi)
Curvatura gaussiana totale = 2π [2 – 2 (numero di buchi) ]
• Il messaggio contenuto nel teorema ‘egregio’ di Gauss è alla base
delle generalizzazioni a spazi (o spazi-tempo) di dimensione > 2 . Le
varietà riemanniane n-dimensionali sono spazi dotati di una metrica
intrinseca (tensore metrico) la cui conoscenza permette di calcolare,
punto per punto, tutte le quantità legate alla curvatura senza ricorrere
all’ uso di ‘arene esterne’ in cui ‘immergere’ questi oggetti geometrici.
• Controparte di K per le varietà riemanniane: curvature sezionali, a loro
volta derivabili dal tensore di Riemann. Da quest’ ultimo si costruisce il
termine geometrico delle equazioni di Einstein ( Rik – ½ R gik )
31