INFORMAZIONE
TOPOGRAFIA.
DAL 3-4-5 DEI MURATORI AL CERCHIO SARDO E ALLA “PROCEDURA BORUTTA”
In attesa della separazione dei percorsi fra scienza teorica ed applicata, una
delle attività più affascinanti, probabilmente fra le più antiche del mondo, fu misurare: grazie all’osservazione ed alle misure fu realizzata la prima base di conoscenza,
che ci aiutò a costruire quello che siamo oggi. In omaggio a chi venne prima di noi,
abbiamo riesumato uno strumento elementare di antiche origini e bassissimo costo,
con il fine di valutare se un metodo antico si possa utilizzare ancora oggi, noto il
margine di errore.
Rispetto a qualche millennio fa abbiamo a disposizione, non da molto, Google
Earth (GE in seguito), uno straordinario strumento gratuito di misura che ci consente
rapidamente di ottenere distanze ed angoli orientati su tutto il nostro pianeta. In
particolare GE ci consente di visualizzare in qualunque punto del globo, in pochi
secondi, sia la direzione dell’asse di rotazione del pianeta, il Nord, che il valore
dell’angolo rispetto al Nord di una qualunque altra direzione, o Azimut. L’azimut è
restituito attualmente in gradi decimali, riferiti anche come decimal degrees o dd. La
precisione di GE è al centesimo di grado decimale, per intenderci nel formato 359.99;
il verso di misura è antiorario. Est risulta a 90°, Sud a 180°.
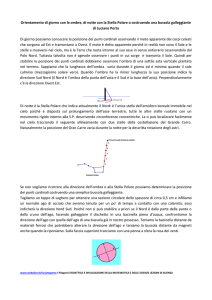
Tramite GE è stato stimato rispetto al Nord l’angolo dell’asse di un fabbricato
(Azimut), utilizzando lo strumento disponibile righello-linea; il
fabbricato è quello della Essei Servizi a Siamaggiore. È risultato un angolo di circa 25,25° decimali verso Est rispetto al
Nord geografico. La precisione ottenuta in questo modo risulSS 131
ta limitata dalla definizione delle foto e dal fatto che il fabbrikm 100
cato ha modeste dimensioni.
L’errore in un caso del genere è stato stimato in circa
0,20-0,25 gradi decimali: non si riesce a stabilire se 25,35°dd
sia migliore di 25,15°dd con una trentina di metri a disposizione: dipende dalla linea che si prende come riferimento. Effettuare questa misura ha comunque richiesto meno di un minuto.
Senza Google Earth, gratuito ma con dietro qualche bilione di
dollari, o senza un sistema GPS topografico da migliaia di euro
saremmo riusciti rapidamente ad eseguire la stessa misura?
Per fare delle misure assolute rispetto al Nord geografico è fondamentale individuare la direzione del Nord geografico. Prima di continuare, se non potete utilizzare un’attrezzatura topografica, chiedetevi come riuscireste a tracciare la direzione del Nord geografico con gli strumenti disponibili, con
quale precisione ed in quanto tempo.
Nel nostro percorso scolastico ci hanno indicato vari metodi
empirici: il muschio, la bussola, la stella polare etc. Tralasciamo il primo: in Sardegna
il muschio non è diffusissimo ed in ogni caso il metodo è molto approssimativo.
Vediamo gli altri.
La bussola era ed è un rivelatore di campo magnetico facilmente realizzabile
con una calamita sospesa ad un filo o poggiata sull’acqua tramite un supporto di
legno. Normalmente la calamita si allinea parallelamente al campo magnetico terrestre; se ciò non succede, è perché vi sono alterazioni locali del campo. Come noto da
tempo, la bussola indica una direzione, tuttavia la direzione indicata non è quella del
Nord geografico (90°N, 0°E) per via della declinazione magnetica. Vi è una differenza fra le direzioni dovuta al fatto che il Nord magnetico ed il Nord geografico -
pagina
17
GLI AUTORI.
L’ingegnere Giorgio Demontis
svolge la libera professione presso
ESSEI Servizi srl, società di ingegneria.
telefono: 328.8967225
e-mail: [email protected].
I geometri Filippo Contini
(339.6125766, [email protected])
e Roberto Defendente (328.2799196,
[email protected])
lavorano con la Geo's Team di Oristano.
Polo Nord
asse rotazione
angolo
Google Earth
25°, 25 DD
ESSEI Servizi
z.i. Siamaggiore
Illustrazione 1. La sede della ESSEI Servizi
(39°58'14.89"N, 8°37'37.57"E)
116
Tracciare il Nord geografico
con metodi empirici antichi e moderni
116
INFORMAZIONE
Topografia
per il quale passa l’asse di rotazione - non coincidono, come
evidenziato nell’illustrazione 2. Questa differenza angolare
tra la direzione del Nord magnetico e quella del Nord geoNord
geografico
grafico viene chiamata declinazione magnetica.
La posizione in coordinate del Nord magnetico 2010 è
stata ripresa dalle pubblicazioni IGRF-11 (International
Geomagnetic Reference Field) e riportato come segnaposto
su GE. L’angolo misurato tramite GE indica 356,21 dd (3,79°
Ovest). La distanza fra i due poli risulta di circa 700 km. La
declinazione
differenza di direzione risulta inoltre essere parecchio ballemagnetica 2010
3.79° DD Ovest
rina nel tempo. Nel 1500 pare che il Nord magnetico fosse
ubicato ad Est, sul confine russo-svedese (Murmansk). Oggi
risulta al largo del Canada. (85,0°N, 132,6°W nel 2010). Il
percorso della migrazione del Nord magnetico dell’ultimo secolo è riportata nell’illustrazione 3.
ESSEI
Ovviamente esistono online dei software che calcolano
la declinazione magnetica in base alle coordinate geografiche. Se alla pagina http://www.ngdc.noaa.gov/geomagmodels/
Declination.jsp inserite le coordinate ESSEI (39 58 14 N - 8
37 37 E), troverete che la declinazione in tali coordinate il 23
ottobre 2010 risulta 1°26’ Est (+1.43 dd) con variazione 0,6’ Est/anno. NOOA è un
Illustrazione 2: la declinazione magnetica
sito governativo USA e si basa anch’esso su IGRF-11.
evidenziata su Google Earth. Rispetto alla
Il segnaposto del Nord magnetico 2010 messo su GE è sicuramente ad ovest di
sede della ESSEI Servizi, sono riportate le
congiungenti con il polo Nord e con il Nord
Siamaggiore; la direzione che dovrebbe assumere la bussola secondo NOOA si trova
magnetico IGRF-11 2010.
ad Est. Sul tutto non vi sono dubbi, in quanto il calcolatore di declinazione NOOA fa
vedere una bella bussola su Google Maps che non lascia incertezze sulla direzione e
sulle coordinate immesse, come riportato nell’illustrazione 4.
Per sapere a chi dare retta, non è rimasto che svolgere una verifica sul campo
con la bussola. Sono state quindi eseguite delle misure dell’angolo
fra l’asse del fabbricato e la direzione indicata dalla bussola. Con lo
Emisfero
scopo di consentire a tutti la ripetizione delle misure, non sono stati
settentrionale
adoperati strumenti particolari. È stato necessario eseguire delle
misure a terra ad una certa distanza dal fabbricato. La precisione
delle due bussole graduate utilizzate è dell’ordine di un grado
sessagesimale.
Tracciare la perpendicolare con un metodo antico. Per
riportare l’asse del fabbricato a terra e quindi eseguire delle misure
comode e ripetibili abbiamo usato un metodo antico arrivato ai giorni nostri, quello che i muratori ed i carpentieri ancora oggi chiamano
il 3-4-5. Questo metodo consente di tracciare la perpendicolare ad
polo magnetico
una linea e quindi ad un lato dell’edificio: tramite esso troveremo la
perpendicolare al fabbricato, direzione che servirà per verificare le
altre misure. Il 3-4-5 è diverso dal metodo insegnatoci a scuola per
polo geomagnetico
trovare la perpendicolare: non richiede il compasso. Per applicarlo
modernamente servono al massimo tre persone, ognuna con un metro
flessibile tipo Stanley. Il metodo si basa sull’unico triangolo rettangolo con i lati di lunghezza pari a tre numeri naturali consecutivi.
Tale triangolo rettangolo ha due cateti di lato 3 e 4. Secondo Pitagora,
2+42=9+16=25, da cui si deduce che l’ipotenusa è pari a 5. Da qui
3
Qui sopra (illustrazione 3):
il nome 3-4-5.
deriva del Nord Magnetico
Non esistendo alcune migliaia di anni fa un metro ufficiale si
come da dati IGRF.
A destra (illustrazione 4):
utilizzavano misure relative: tagliando 3+4+5=12 legni tutti uguali si
declinazione magnetica
realizzava facilmente la dima per lo schema 3-4-5, pur senza sapesecondo NOOA presso
re la misura assoluta dei legni. Se il metro pieghevole a stecche da
la Essei a Siamaggiore.
muratore avesse 12 stecche (240 cm) invece che 10, si potrebbe
usarlo egregiamente per lo scopo.
Anche se oggi vi sono sistemi economici basati sul laser, abbiamo tracciato la perpendicolare al lato Sud dell’edificio con il 3-4-5,
Nord magnetico
2010
pagina
18
INFORMAZIONE
Coordinate di calcolo 39° 58' 14" N , 8° 37' 37" E – 39.97°, 8.63° deg
declinazione
NOOA
il 30 giugno
deriva
annuale
angolo tra
le declinazioni
GE-NOOA
x
x
-11°11' (W)
0° 4' E
x
-96,70
x
x
-10°14' (W)
0° 8' E
x
74,60
-100,80
x
x
-4°17' (W)
0° 5' E
x
1960
75,30
-101,00
x
x
-3°20' (W)
0° 5' E
x
1990
78,10
-103,70
x
x
-0° 30' (W)
0° 5' E
x
2000
81,00
-109,70
350,31
-9,69°
0° 27'
0° 5' E
10,14
2005
83,10
-117,80
353,17
-6,83°
0° 54'
0° 5' E
7,73
2010
85,00
-132,60
356,12
-3,88°
1° 24'
0° 6' E
5,28
Gradi minuti
+ Est
- Ovest
GG mm
Lat N, dd
Lon W, dd
1900
70,50
-96,20
1910
70,80
1950
Posizione del polo magnetico
secondo IGRF-11
International Geomagnetic Reference Field
angolo su
Google Earth
+verso Est
Decimal Degrees
direzione Ovest
Dec Deg
per eseguire una ricostruzione storica mantenendo gli errori compatibili con il passato, e anche perché non tutti abbiamo quel tipo di strumento. La bussola migliore
adoperata ha due scale. La prima ha tacche ogni 5°, la seconda ogni 360/
(64x5)=1,125°.
È stato rilevato un angolo di circa 4,8x5x1,125, ovvero circa 27° gradi di inclinazione Ovest, fra la perpendicolare al lato Sud dell’edificio e la direzione dell’ago
che punta al Nord magnetico. L’asse
del fabbricato ESSEI ha una direzione
25,25° Est (DD) rispetto al Nord geografico, come da misurazione effettuata
tramite GE.
La differenza fra la direzione del
Nord stimata con la bussola e la direzione rispetto al Nord dell’asse del fabbricato è risultata pari a 27°-25,25°
ovvero 1,75° Ovest. Tale valore è diverso sia dall’angolo rispetto alla posizione del Nord Magnetico nel 2010
misurato su Google Earth pari a
356,21° o 3,79° dd Ovest (3°47’ W)
sia da 1,43°dd Est come
calcolato da NOAA per
il 20 ottobre 2010. In
base a quanto rilevato,
sembra tuttavia che la declinazione sia ad Ovest, e non ad Est come
indicato dal software online NOOA.
La determinazione del Nord geografico tramite una misurazione basata sulla bussola presuppone la conoscenza della declinazione
magnetica e della sua variazione nel tempo, fatto che, alla luce di
quanto visto oggi, migliaia di anni fa fece propendere - per l’effettuazione di misure di precisione - verso l’utilizzo di altri metodi più semplici, ripetibili ed affidabili.
Va ricordato che la precisione raggiunta da alcune misure antiche fu non solo notevole, ma anche straordinaria, sia per l’ingegno
che per i mezzi di cui allora si disponeva. A parte la misurazione del
raggio terrestre (6314 km contro i 6356 km misurati oggi) ottenuta
da Eratostene fra il 240-230 AC contando i passi di cammello su una
distanza di 800 km, va ricordato senz’altro Ipparco di Nicea, che nel
pagina
19
Gradi Decimali
Dec Deg
Tabella 1. Sintesi delle posizioni
del Nord Magnetico
e della declinazione magnetica
secondo NOOA in varie date.
Illustrazione 5 (a sinistra): schema 3-4-5.
In basso (illustrazione 6): stima dell'angolo
fra l'asse della Essei servizi ed il Nord.
116
declinazione
magnetica
via segnaposto
anno
116
INFORMAZIONE
Topografia
130 AC stimò la precessione degli equinozi pari a 46’ l’anno, contro i 50,26’ odierni,
e che per primo documentò mediante calcoli la durata dell’anno sidereo pari a
[365+1/4+1/144 giorni] 365 giorni 6 ore e 10 minuti (oggi 365 giorni 6 ore 9
minuti e 9 secondi). Le opere originali di Ipparco risultano disperse, come in genere
tutto ciò che prima di Tolomeo riguardò gli studi sul sole ed il sistema solare. Un
dispositivo quale quello di Antikythera, custodito e ricostruito funzionante al Museo
nazionale di Atene, trascina con sè quintali di domande.
La stella polare. L’osservazione del moto notturno delle stelle evidenzia
la presenza di un centro di rotazione, per cui la stella candidata ad indicare il
centro di rotazione era quella che ruotava meno delle altre, era luminosa, stava
in una costellazione. Questa stella prende il nome di stella polare. La scelta era
sicuramente influenzata dalla luminosità e rintracciabilità della stella, più che
dalla precisione. Attualmente la stella polare di riferimento sta nella costellazione dell’Orsa Minore (piccolo carro). Lo scarto attuale della direzione vale circa
0,75 gradi rispetto al nord geografico.
stella
Illustrazione 7. Moto delle stelle nel cielo.
Tabella 2 e illustrazione 8 (in basso):
stelle polari nel tempo
(da Wikipedia, edizione italiana).
magnitudine
dal
al
durata
Vega
-13050
-11050
2000
0,03
3,9
Pi.greco Herculis
-11050
-8850
2200
3,2
6,8
Eltanin
-8850
-8150
700
2,2
7,6
Eta Herculis
-8150
-6550
1600
3,5
7,9
I Draconis
-6550
-2750
3800
3,3
3,1
Pherkad
-2750
-2650
100
3
9
Kochab
-2650
450
3100
2,1
3,7
Polaris
450
3100
2650
2
0,4
apparente
angolo
L’attuale stella polare, salvo imprevisti, regnerà fino al 3100 DC, cedendo
quindi il ruolo ad Alrai. Le stelle precedenti alla polare hanno avuto errori molto
maggiori, dell’ordine di qualche grado. Ad esempio Vega, la stella polare di 13.000
anni fa, aveva un errore di almeno 3.9°. Sicuramente si evidenzia che quando nacque Nostro Signore la stella polare (Kochab, allora) aveva almeno 3-4 gradi di
errore.
Per via del trottolamento nello spazio dell’asse di rotazione terrestre vi sono
state diverse stelle polari più o meno vicine all’asse di rotazione.
Il tempo in cui l’asse ripassa per lo stesso punto è molto superiore alla vita umana: ha un periodo pari a circa 26.000 anni.
L’ubicazione del Nord geografico tramite la stella polare, essendo legata alle vicende dell’asse di rotazione terrestre, aveva una
precisione legata alla stella di riferimento. Per capire ciò che
accade in 26.000 anni rovesciamo ed acceleriamo il tutto fino a
farlo avvenire in pochi secondi: immaginate di essere ormeggiati
in barca a vela e di guardare dove punta l’albero nel cielo. Normalmente tutto dondolerà in cerchio, puntando varie stelle.
Il cerchio sardo. Un sistema più pratico per effettuare
misure angolari orientate (azimut) ripetibili ed utilizzabili sul pianeta fu utilizzare come riferimento la direzione dell’asse di rotazione, ovvero il Nord geografico. Ciò implicò l’identificazione del
meridiano, la linea passante per il punto di misura e per i due
poli di rotazione, Sud e Nord. Ma era possibile identificare il
meridiano senza strumenti moderni? E con quale precisione?
Il meridiano, e quindi il Nord, è risultato identificabile facilmente proprio usando un metodo vecchio, con oltre 5.000 anni
sulla groppa, detto il cerchio. Il metodo risulta essere stato adoperato in India, Egitto, Nord America. L’uso in Italia è citato da
pagina
20
21
116
pagina
INFORMAZIONE
Vitruvio, l’autore del De Architectura, I secolo a.C.; la
Siamaggiore (OR), 25 settembre 2010 - 39.97°N, 8.63°E, ora legale
paternità sarda attribuita deriva anche dal fatto che in
A alle 11.17 - B alle 15.16
quest’isola per la prima volta è stato riutilizzato e ne
sono stati misurati i risultati, originando una nuova vita
per il metodo. Vediamo quindi come funziona questo
Cerchio passante per A
novello Frankenstein e con quale precisione.
Centro in C
Per trovare il Nord tramite il cerchio sardo occorre semplicemente un’ombra con origine stabile.
Per procurarla possiamo utilizzare come asta un tondo d’acciaio da cemento armato da 100 cm, oppure
una canna. Basta piantare il tondo in terra, verticalC
mente, e l’ombra col sole appare subito: non sono
A
necessarie batterie. Il metodo sfrutta la simmetria
dell’ombra rispetto al transito sul meridiano. Il senno
di poi ha evidenziato che conviene usare per l’asta
M
una stecca di legno: la bussola è risultata parecchio
disturbata dall’acciaio.
Nord
A Siamaggiore il mezzogiorno solare 2010 al solstizio di giugno si è verificato verso le 13.27 dell’ora
B
legale o le 12.27 dell’ora solare. Il ritardo di un’ora e
mezza del solstizio è dovuto all’ora legale ed al tempo
di rotazione rispetto al fuso orario: all’interno del fuso
orario, il mezzogiorno del segnale orario è contemporaneo in tutto il fuso. Quando il
Illustrazione 9.
segnale orario, caso di ora solare, al bip lungo dichiara che è mezzogiorno è mezzoDeterminazione del Nord
giorno circa a Catania, dove passa il meridiano 15°. Il giorno del solstizio d’estate
per via geometrica.
Metodo basato
abbiamo dovuto aspettare che la terra ruotasse per circa mezz’ora affinché il punto
sulla simmetria dell’ombra,
dove avevamo i piedi, Siamaggiore (8°37’), si allineasse con la congiungente fra il sole
detto “cerchio sardo”.
ed il centro della terra. Se è in vigore è l’ora legale, bisogna aggiungere un’altra ora.
Ad esempio, all’equinozio di autunno a Siamaggiore l’ombra si allinea con il meridiano
nell’intorno delle 13.17 circa dell’ora civile.
Avendo ben chiaro questo, infiggiamo l’asta nel terreno prima del mezzogiorno solare e mettiamola approssimativamente a piombo in direzioni ortogonali, ad
occhio, mediante un filo a piombo od addirittura tramite un sofisticatissimo livello a
bolla. Se vi è sole, l’asta proietterà immediatamente un’ombra sul terreno. Va segnato il punto A in cui termina l’ombra
dell’asta e quindi va tracciato il cerchio passante per il punto
A che abbiamo segnato, con centro nel punto C, l’asse dell’asta. Si può usare uno spago ed un chiodo oppure, come
fatto da noi, un marker indelebile (a parole).
Se rimaniamo a guardare, noteremo che nel tempo la
punta dell’ombra ruota attorno all’asta e si accorcia, per poi
riprendere ad allungarsi. In pratica, dovendo aspettare che l’ombra ripassi sul cerchio, tanto vale andare a pranzo. Qualche
tempo dopo, quando la punta dell’ombra ripassa sul cerchio
tracciato la mattina, va segnato il secondo punto B. Ora è fatta.
Tracciamo il segmento congiungente A con B, quindi determiniamo il punto di mezzo M del segmento AB. La congiungente il
punto di mezzo M con il centro del ferro C corrisponde alla direzione del Nord geograIllustrazione 10. Misura del cateto
fra direzione Nord
fico. Il metodo è stato applicato presso la sede della Essei Servizi il 23 giugno 2010 (il
e perpendicolare al fabbricato.
21 ed il 22 era nuvoloso). L’errore riscontrato rispetto a quanto determinato con GE,
anche senza aver utilizzato dei particolari accorgimenti, ovvero piazzando il ferro in
verticale ad occhio, utilizzando uno spago etc, è risultato contenuto.
La direzione del Nord rispetto all’asse del fabbricato, stimata tramite GE con
un incertezza di circa 0,20-0,25 dd, è risultata pari a 25,25°dd. Tramite il cerchio
sardo abbiamo ottenuto arcTan (9,5/20)=arcTan (0,475)= 25,41° dd. La misura
dell’angolo è stata eseguita inizialmente con una bussola e quindi mediante misurazioni geometriche dirette, in quanto la bussola si è rivelata troppo approssimata.
È stato usato un metro da muratore a stecche da 20 cm. Abbiamo misurato,
116
INFORMAZIONE
Topografia
Dall’alto verso il basso:
pannelli del render di Progecad 2009
(illustrazione 11); immissione delle
coordinate Essei (illustrazione 12);
calcolo dell'ora in cui ad Essei il 23 ottobre
2010 Azimut = 180 (illustrazione 13).
pari a 9,5 cm, il cateto corto del triangolo rettangolo formato dalla perpendicolare al
fabbricato e la direzione del Nord trovata (ipotenusa). Il cateto lungo la perpendicolare al fabbricato è stato preso pari a 20 cm. La perpendicolare è stata trovata con
l’ausilio di una squadretta scolastica in plastica a 90°. L’angolo corrispondente alla
tangente è stato ricavato tramite una calcolatrice scientifica da 10 euro. La misura
diretta sul terreno con un goniometro scolastico dà una precisione molto minore per
via dell’inevitabile spessore delle linee di tracciamento. La differenza con GE è risultata pari a 25,41-25,25=0,16 dd, circa 10 minuti sessagesimali.
Il fatto che il valore ottenuto risulti all’interno dell’incertezza della misura eseguita
con GE, non rappresenta la precisione del metodo, dato che l’abbiamo comparato con
una misura approssimata. L’informazione ottenuta finora è che il risultato ottenuto è all’interno dell’approssimazione di GE, fatto peraltro positivo e incoraggiante; tuttavia servono sicuramente dei riscontri migliori
per valutare la bontà del metodo.
Trovare rapidamente il
Nord: il metodo “Borutta”. La
procedura vista precedente ci fornisce il Nord praticamente senza
l’uso di tecnologia ma presuppone
un impegno diretto di tempo di circa un’ora ed indiretto di diverse
ore, essendo costretti a rimanere
nei dintorni del luogo di misura per
effettuare la seconda lettura. Durante il tracciamento di un grande
orologio solare a Borutta (SS) è
stato sviluppato un metodo differente, che richiede meno tempo ed
ha un costo accettabile, per cui lo
proponiamo.
Questo metodo si basa sull’utilizzo di un computer portatile e di un software
tipo Autocad (costo complessivo minimo dell’insieme circa 1.000 euro). Il CAD utilizzato è Progecad Professional 2009 (costo circa 500 euro). Normalmente un tecnico ha già entrambi, per cui gli investimenti da fare sono equivalenti a quelli del
cerchio sardo. Sorvoliamo sul costo dell’orologio atomico dell’ex Istituto Nazionale
Galileo Ferraris e del segnale orario nazionale.
Fra le opzioni di rendering di Progecad vi è l’illuminazione ed è prevista l’illuminazione solare (tipo di luce distante). Le coordinate del luogo dove siamo le possiamo rilevare tramite Google Earth o - se non abbiamo un collegamento alla rete - con
un GPS stradale da 50 euro (precisione media ormai circa 7-10 m). Note le coordinate del luogo, le immettiamo nel CAD (vedi illustrazione 12). Progecad
consente l’utilizzo di 2 decimali nelle coordinate del luogo, ovvero ha
un passo di 36 secondi d’arco. Questo ad esempio introduce, a
Siamaggiore, una approssimazione media nell’ubicazione del luogo
pari a circa 850 m in longitudine e a circa 1100 m in latitudine. Per
visualizzare e stimare con maggior precisione l’errore planimetrico
locale si può usare sempre Google Earth usando quattro segnaposti
ed il righello-linea, come riportato meglio più avanti.
Metodo diretto. Messe le coordinate del luogo nel CAD si fanno un paio di tentativi per ottenere l’ora per cui l’azimuth risulta 180
(vedi illustrazione 13). Progecad non tiene conto dell’ora legale, per
cui le 12h.09m.49s corrispondono il 23/10/2010 alle 13h.09m.49s
dell’ora legale, quella del segnale orario. Trovata l’ora dell’azimut 180
si va sul terreno e si traccia la direzione dell’ombra all’ora indicata col
CAD, ricordando che va aggiunta un’ora durante il periodo di vigenza
pagina
22
Shadows 3.2.2
Ora passaggio meridiano (hh.mm.ss)
differenza tempo
per 0,01°
8°37'12"
(8.62 dd)
8°37'48"
(8.63 dd)
differenza tempo
per 0,01°
Differenza assoluta
di tempo
fra Progecad
e Shadows
(hh.mm.ss)
13.17.53
00.00.03
13.18.06
13.18.03
00.00.03
00.00.10
13.11.20
13.11.17
00.00.03
13.11.26
13.11.24
00.00.02
00.00.06
23/10/10 (ora legale)
13.09.52
13.09.49
00.00.03
13.09.57
13.09.54
00.00.03
00.00.05
26/10/10 (ora legale)
13.09.31
13.09.28
00.00.03
13.09.34
13.09.31
00.00.03
00.00.03
26/11/10 (ora solare)
12.12.47
12.12.44
00.00.03
12.12.39
12.12.36
00.00.03
00.00.08
Ovest/basso
Est/basso
Ovest/basso
Est/basso
SX
DX
SX
DX
Longitudine da Greenwich
(+EST)
Longitudine da Greenwich
(+EST)
8°37'12"
(8.62 dd)
8°37'48"
(8.63 dd)
23/09/10 (ora legale)
13.17.56
15/10/10 (ora legale)
Latitudine 39°58'12"N – 39,97°N dd
Gli errori legati al “metodo Borutta” dipendono da quattro fattori:
1) l’errore di marcatura sul terreno dell’asse dell’ombra;
2) l’orologio non sincronizzato;
3) in Progecad i valori di latitudine e longitudine sono limitati ai centesimi di grado;
4) la bontà dell’algoritmo di calcolo.
1. Stima dell’errore di marcatura. L’errore del posizionamento è funzione della stagione in cui si misura e dell’altezza e della larghezza dell’asta. Le ombre sono più
corte d’estate e più lunghe d’inverno. All’aumentare dell’altezza dell’asta la punta
della sua ombra diventa sempre meno nitida, probabilmente per via dei fenomeni
ottici legati alle maggiori lunghezze di attraversamento dell’aria.
Si è stimato un errore massimo di 5 mm sulla determinazione dell’asse di un
ombra a distanza 100 cm dal ritto. Su una misura di 100 cm l’errore risulta pertanto stimabile in circa 0,28648° dd o 17’ 11” sessagesimali, ottenuti tramite
Arctan(0.5/100).
pagina
23
Tabella 3. Comparazione delle differenze
di tempo ottenute con due software.
116
Siamaggiore (OR)
sede ESSEI
Progecad 2009
Ora azimut=180 (hh.mm.ss)
INFORMAZIONE
dell’ora legale. In tal modo ottengo direttamente la direzione del Nord
con qualche minuto d’arco di precisione.
alto DX
L’errore dipende dal fatto che l’ombra è calcolata su coordinate
39.98° - 8.63° dd
approssimate al centesimo di grado decimale, che l’algoritmo di calcolo
dell’ombra contiene approssimazioni, che l’orologio (nostro o del pc)
può essere non sincronizzato con l’ora I.N.R.I.M. (ex ora Galileo Ferraris
1109
di Torino). Questo approccio richiede di essere al mezzogiorno solare sul
posto e come contropartita offre la determinazione diretta sul terreno
della direzione. Se invece si vuole stimare la direzione del meridiano in
qualunque momento del giorno, si può adoperare il metodo indiretto.
basso SX
Metodo indiretto. Sfruttando le equazioni di Progecad per deter39.97° - 8.62° dd
basso DX
minare l’angolo, devo semplicemente marcare sul terreno la direzione
39.97° - 8.63° dd
dell’ombra e scrivere l’ora esatta in cui fisso tale direzione sul terreno. A
853
quel punto sono in grado di determinare l’angolo rispetto al Nord dell’ombra segnata, semplicemente immettendo in Progecad le coordinate
del luogo, la data e l’ora (non legale) del tracciamento. Noto l’angolo
rispetto al Nord della direzione rilevata, traccio sul terreno la direzione del Nord Illustrazione 14. Stima delle distanze
geografico, sfruttando il CAD che ho appresso o uno strumento. Il metodo indiretto corrispondenti ad una differenza di 0,01°dd
introduce per forza un ulteriore errore, dovuto alla determinazione indiretta della presso Essei ricavata tramite GE.
direzione Nord, tuttavia ha il pregio di farci tracciare una direzione in qualunque
istante. Questo approccio sembra avere tutte le caratteristiche per diventare un
metodo rapido alternativo per il tracciamento generale di una direzione geograficamente orientata; peraltro nel presente lavoro - per motivi di tempo e spazio carta - il
metodo indiretto non è stato sottoposto a test approfonditi.
116
INFORMAZIONE
Topografia
Illustrazione 15.
Istantanea dell'ombra alle 13h.09m.30s
del 26 ottobre 2010 ad Essei.
Illustrazione 16.
Allineamento fra Nord GPS ed ombra
alle 12h.09m.55s del 13 novembre 2010
a 39°54'26"N, 8°34'25"E
o 39.91dd, 8.57dd.
La stima dei restanti errori si può eseguire appoggiandosi a Google
Earth. In tabella 3 sono stati riassunti alcuni valori calcolati in due punti
distanti un centesimo di grado decimale. I due punti sono stati chiamati
basso SX (Ovest) e basso DX (Est).
2. Stima dell’errore dell’orologio. Se il nostro orologio non è sincronizzato con il tempo campione italiano introdurremo un errore. Secondo
quanto calcolato da Progecad 2009 il giorno 23 ottobre 2010 l’azimut
180 viene raggiunto
• alle 12h 09 m 52s solari con longitudine 8.62 Est (basso SX),
• alle 12h 09 m 49s solari con longitudine 8.63 Est (basso DX).
Da questo si deduce che 52-49=3 secondi di orologio corrispondono in
questo caso a circa 0,01° gradi decimali, 0,6 minuti sessagesimali.
3. Incidenza dell’errore delle coordinate. Il 26 ottobre 2010, alla coordinata basso SX, (8,62 dd Est), l’angolo azimut alle 12 h 09m 28s, ora in
cui transita il meridiano ad 8,63°dd Est, risulta secondo Progecad
179,98°dd. Da quanto esposto si deduce che l’errore dovuto alla posizione risulta
contenuto in circa 0,02° gradi decimali ovvero 60x0,02 = 1’ 12” sessagesimali.
4. Bontà dell’algoritmo di calcolo. L’ora del passaggio al meridiano manifesta differenze anche di una decina di secondi in funzione dell’algoritmo di calcolo, entro circa
0,04° gradi decimali, meno di 3’ sessagesimali.
Errore peggiore stimato. L’errore peggiore che si può commettere risulta quindi 0,29°+0,01°+0,02°+0,04°= 0,36 °dd, ovvero circa 22’ sessagesimali. L’utilizzo
di una macchina fotografica, di un orologio sincronizzato e di un righello può ridurre
le componenti d’errore del posizionamento e dell’orologio. In tal caso l’errore dovrebbe ridursi ad un decina di minuti sessagesimali.
Errore ottenuto su una misurazione. Se sincronizziamo il nostro
orologio o quello del pc col segnale orario nazionale (server ora internet:
ntp.inrim.it) si presume un errore massimo di un secondo nell’indicazione del tempo. Circa un secondo di tempo di errore lo attribuiamo
alla marcatura della punta dell’ombra sul terreno. Gli errori di misura
si possono stimare contenuti entro tre o quattro secondi di tempo, cui
abbiamo visto corrispondere a Siamaggiore circa 0,02° dd o 12’ di
errore.
Per valutare che cosa succeda in pratica, abbiamo adoperato un
orologio radio controllato, quello della stazione meteo montata sul tetto
della Essei Servizi (PWS-Ioristan4), insieme ad una macchina fotografica. La differenza fra il Nord trovato con il metodo basato sul CAD e
quello trovato con il cerchio sardo è risultata pari a meno di un millimetro
verso Est ad 83 cm dall’asta. Ora arcTan (0,1/83)= arctan (0,00121)= 0,069 dd,
circa 4’ 9”. La differenza di direzione fra i due metodi analizzati risulta all’interno del
valore di errore massimo stimato, 23 minuti sessagesimali, e in valore assoluto è
contenuta.
Valutazione tramite GPS. Per verificare il “metodo Borutta” è stata eseguita una
prova. Sono stati posizionati due punti a longitudine costante ed è stato verificato l’allineamento dell’ombra con tale direzione. È stato usato un GPS della Trimble Navigation,
modello Trimble R6, un aggeggio da circa 10.000 euro. I punti GPS sono stati battuti in
tempo reale grazie al collegamento via cellulare alla rete di punti GPS fissi SARNET. Il
luogo scelto per le prove è vicino alla sede Geo’s Team, proprietaria del GPS, precisamente in prossimità del punto IGM95 codice 217905, ubicato ad Oristano in viale Repubblica. Il primo punto utilizzato è un chiodo sul marciapiede alla base di un palo d’illuminazione, l’altro, a circa 20 m, nel parcheggio adiacente, su asfalto.
Il 13 novembre 2010 è stata quindi tirata una lenza fra i due punti; come ombra è
stata usata quella dell’asta in carbonio del GPS, messa a bolla su un treppiede a filo con
la lenza sul lato EST. L’asta ha un diametro di 32 mm, misurati col calibro, pertanto l’asse
dell’ombra era atteso a 16 mm dalla lenza. Le foto non sono tecnicamente impeccabili:
per leggerle è stato necessario ritoccarle, come evidente nell’illustrazione 16.
La differenza è stata stimata contenuta entro 2 mm; l’angolo relativo, essendo
l’ombra dell’asta lunga 2520 mm, vale atan(2/2520) circa 0,04547 dd, 2’44”
pagina
24
INFORMAZIONE
NORD via CAD
0,125 dd Ovest (ombra del 26.10.2010)
NORD cerchio sardo
0,16 dd Ovest (ombra del 23.6.2010)
NORD GEOGRAFICO da Google Earth
0 gradi
NORD bussola
1,75 dd Ovest (bussola)
NORD magnetico 2010 IGRF-11
angolo da segnaposto su Google Earth
3,88 dd Ovest
DECLINAZIONE calcolata da NOOA IGRF-11
1,43 dd Est (20 Ott 2010)
ASSE fabbricato ESSEI
25.25 dd Est (GE)
osa
ldo
mis
ure
25.25°
cap
Discussione.
NORD GEOGR AFICO
OVEST
EST
Sul marciapiede Essei, tre metodi abissalmente diversi come approccio hanno fornito
la direzione del Nord con valori compresi fra
25.25°dd e 25,41°dd. L’incertezza maggiore
riguarda in fondo quella rilevata tramite Google
Earth: 25,25° dd per via della intrinseca difficoltà di misurazione. La media delle tre misure
risulta 25.345° dd, quella delle due misure
(25,41° e 25,375°) più vicine fra loro
SUD
25,393°dd. I primi riscontri effettuati in altro
luogo con il GPS, assunto come strumento di
riferimento, hanno confermato la discreta preIllustrazione 17. Sintesi grafica
cisione ottenibile con i metodi empirici.
Le differenze fra i due metodi a bassa tecnologia utilizzati ed il GPS sono delle misurazioni effettuate ad Essei.
risultate contenute in qualche minuto sessagesimale. La bussola e la stella polare
hanno teoricamente errori di almeno un ordine di grandezza superiore.
Conclusioni.
Il metodo del “cerchio sardo” è risultato molto robusto ed è straordinario il rapporto fra costo dell’hardware utilizzato e precisione ottenibile. Il “metodo Borutta“ proposto
prevede l’utilizzo del CAD, è molto semplice e ha dimostrato di essere affidabile e
potenzialmente in grado di raggiungere buone precisioni. L’errore principale è risultato
imputabile al posizionamento sul terreno ed all’algoritmo di calcolo dell’ombra.
Quanto sperimentato è risultato molto promettente. Una volta verificato in
tutte le situazioni, probabilmente basterà un GPS stradale con apposito SW (parecchi GPS stradali si possono trasformare via software in un pocket pc con Windows
CE), oppure un pc con CAD o altri programmi, o ancora un’applicazione per iPhone,
per trasformare una qualunque ombra in una direzione orientata con buona precisione. L’orologio sincronizzato al secondo è presente intrinsecamente nei GPS ed è
ottenibile nei pc tramite la sincronia con un server ora internet.
Contributo Inarcassa in fattura al 4%
Nuovo codice IBAN per l'Ordine
Il contributo Inarcassa sulle fatture emesse da ingegneri e architetti è passato dal 2 al 4%, a partire dal 1º gennaio 2011. Sul numero 4/
2010 del notiziario InarcassaNews Medio Campidano - scaricabile dal
sito internet dell’Ordine - sono stati pubblicati alcuni utili schemi di fattura che prendono in considerazione diverse ipotesi, per iscritti e non
iscritti alla Cassa (fatturazione a titolare di codice fiscale; fatturazione a
titolare di partita Iva; fatturazione a ingegneri o architetti con partita
Iva, a società di ingegneria, ad associazione di professionisti), anche
per i “contribuenti marginali”, secondo la Finanziaria 2007.
La Banca di Credito Sardo (Gruppo Intesa-San Paolo) nei mesi
scorsi ha riorganizzato la propria rete di sportelli a Cagliari. La filiale di
via Pergolesi è stata accorpata a quella di largo Gennari angolo via
Tuveri. Di conseguenza dal 25 ottobre 2010 per tutti i bonifici bancari a
favore dell'Ordine è necessario indicare un nuovo codice IBAN. La quota albo, ad esempio, si può pagare con bonifico sul conto corrente
numero 100000011140, intestato all'Ordine degli Ingegneri della provincia di Cagliari, presso Banca di Credito Sardo, largo Gennari angolo
via Tuveri - Cagliari (IBAN: IT73 X030 5904 8281 0000 0011 140).
pagina
25
116
sessagesimali. Si può pertanto affermare che ai
fini del tracciamento del Nord geografico su piccole distanze (2-3 m) i risultati ottenuti con questi metodi empirici sono paragonabili a quelli
ottenibili con il GPS.
L’ora del transito al meridiano, 12h 09m
55 s, è stata ottenuta da effemeridi calcolate su
coordinate ai secondi sessagesimali (39°54’26”N,
8°34’25”E) tramite il programma Shadows 2.3.3.
Progecad avrebbe fornito come orario 12h 09m
59s, con 4 secondi di differenza.
I prossimi test prevedono il tracciamento
di varie direzioni utilizzando l’ombra e la successiva verifica di quanto tracciato mediante
ribattitura con il GPS.
116
INFORMAZIONE
Topografia
La nostra vera sfida è stata rientrare per un poco in contatto con le difficoltà di
misurazione del nostro recente e meno recente passato. Quanto fatto ci ha regalato
la percezione del fatto che ripercorrere, anche per gioco, le strade seguite dai nostri
predecessori ci consente di comprenderle meglio, grazie alla migliore conoscenza
dei metodi che avevano a disposizione e delle relative difficoltà.
Risolvere oggi i problemi di allora è molto facile, con tutto quello che abbiamo
a disposizione: basti pensare che oggi non dobbiamo costruire una squadra a 90° o
forgiare un pezzo di metallo diritto, né costruirci una bolla o un metro. La parte
difficile resta capire come ci si ingegnò per risolvere i problemi con i limitati strumenti a disposizione.
Quanto esposto costituisce semplicemente uno dei possibili approcci alla ricostruzione di quanto successo nella nostra storia tecnica, molte cose del passato sono
ormai praticamente abbastanza sconosciute tanto da sembrare quasi magiche. Avete
qui visto come sia possibile utilizzare un navigatore stradale ed un pc - due oggetti
ormai abbastanza comuni e di costo medio basso - per tracciare sul terreno reale con
buona approssimazione una direzione reale orientata usando un trasduttore solare da
quattro soldi. Al primo impatto, anche per un tecnico, tutto questo ha un po’ l’aria di
una stregoneria, pur derivando dall’applicazione di conoscenze consolidate.
Il cerchio sardo rappresenta sia un esempio di applicazione di geometria con
risvolti non astratti per le scuole sia un gioco da fare al mare, disegnando sulla sabbia.
Il resuscitare un sapere del passato, che per la sua semplicità e precisione merita
sicuramente di sopravvivere nel tempo, è un debito che speriamo di aver onorato.
Giorgio Demontis
Filippo Contini
Roberto Defendente
pubblicità
keykom dati BN 195x135.pdf
pagina
26