ANGOLI OPPOSTI AL VERTICE ANGOLI GENERATI DA DUE RETTE PARALLELE
CON UNA TRASVERSALE SOMMA DEGLI ANGOLI INTERNI DI UN TRIANGOLO
di Luciano Porta
Il percorso parte dalla dimostrazione attribuita a Talete del teorema dell’ uguaglianza degli angoli opposti al vertice,
prosegue con lo studio delle proprietà degli angoli generati da due rette parallele tagliate da una trasversale e giunge alla
meta fondamentale del teorema attribuito alla scuola pitagorica della somma degli angoli interni di un triangolo.
Questo percorso, opportunamente adattato per non sovraccaricarlo di un formalismo fuorviante, può essere compiuto anche
da alunni della prima classe della scuola secondaria di primo grado, indicando gli angoli con numeri e evidenziandoli con
archetti colorati (di uguale colore quelli di uguale ampiezza).
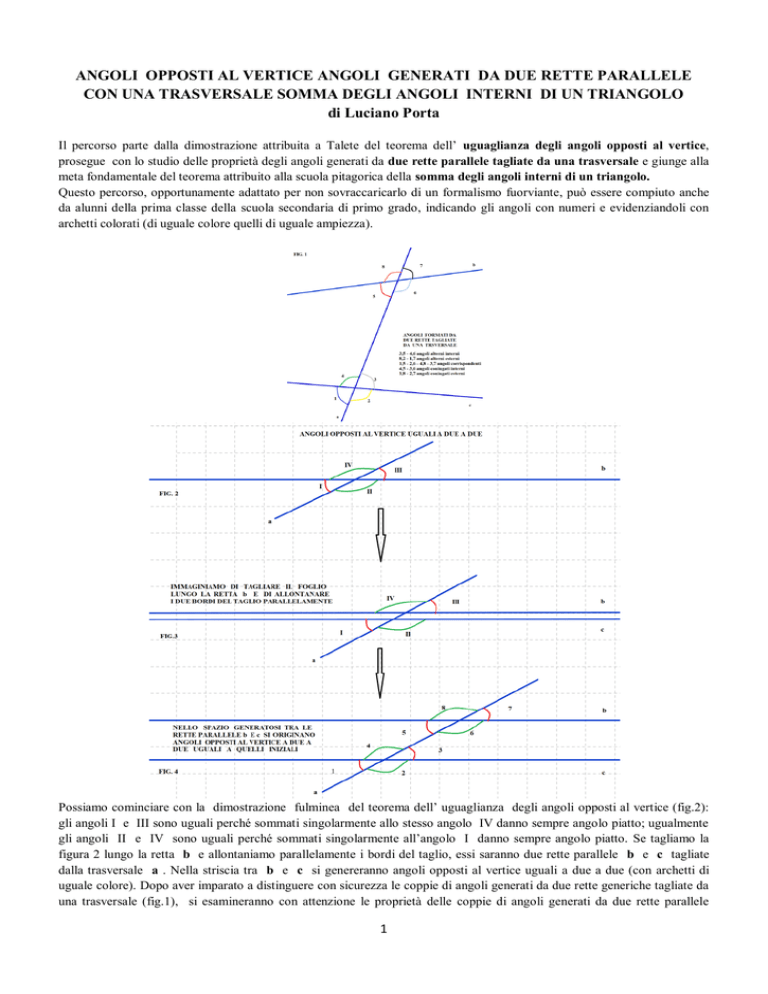
Possiamo cominciare con la dimostrazione fulminea del teorema dell’ uguaglianza degli angoli opposti al vertice (fig.2):
gli angoli I e III sono uguali perché sommati singolarmente allo stesso angolo IV danno sempre angolo piatto; ugualmente
gli angoli II e IV sono uguali perché sommati singolarmente all’angolo I danno sempre angolo piatto. Se tagliamo la
figura 2 lungo la retta b e allontaniamo parallelamente i bordi del taglio, essi saranno due rette parallele b e c tagliate
dalla trasversale a . Nella striscia tra b e c si genereranno angoli opposti al vertice uguali a due a due (con archetti di
uguale colore). Dopo aver imparato a distinguere con sicurezza le coppie di angoli generati da due rette generiche tagliate da
una trasversale (fig.1), si esamineranno con attenzione le proprietà delle coppie di angoli generati da due rette parallele
1
tagliate da una trasversale. Gli allievi non impareranno passivamente a memoria, come solitamente accade, ma ricaveranno le
proprietà col ragionamento:
-
coppie di angoli alterni interni uguali
coppie di angoli alterni esterni uguali
coppie di angoli corrispondenti uguali
coppie di angoli coniugati esterni supplementari (conviene considerare prima i coniugati esterni di quelli interni)
coppie di angoli coniugati interni supplementari.
Ora possiamo affrontare uno dei teoremi fondamentali della geometria euclidea: la somma degli angoli interni di un
triangolo è un angolo piatto.
Gli allievi possono avere una prima intuizione di esso in modo sperimentale piegando, come indicato nelle figure 5, 6, 7, 8 ,
un triangolo di carta.
Poi affronteranno la dimostrazione rigorosa, ma priva di eccessivi formalismi (fig. 9):
Tracciando la retta a parallela alla retta b e passante per C, si generano l’angolo 1 bis (è uguale all’angolo 1 perché
alterni interni) e l’angolo 2 bis ( è uguale all’angolo 2 perché alterni interni):
essendo 1 bis + 3 + 2 bis = angolo piatto, sarà 1 + 3 + 2 = angolo piatto .
www.webalice.it/lucianoporta i Pitagorici DIDATTICA E DIVULGAZIONE DELLA MATEMATICA E DELLE SCIENZE LEZIONI TRE
2










