CLASSE QUINTA GINNASIO
1. La somma degli angoli interni di un ottagono è:
a) un angolo piatto
b) un angolo giro
c) quattro angoli piatti
d) tre angoli giro
e) otto angoli piatti
2. Un numero intero tale che la differenza tra il suo quadrato e i 3/2 del numero stesso sia
uguale a 52 è:
a) 8
b) 15
c) –13/2
d) Non esiste alcun numero intero che soddisfi la relazione
e) Nessuna delle altre quattro risposte
3. L’equazione x(a − 3) = 2a 2 − 6a ha per soluzione:
x = 2a 2 − 6 a + 3
x = 2a per a diverso da 3
x = 2a per a diverso da zero
x = a per a diverso da zero
2a 2 − 6a
e) x =
a −3
a)
b)
c)
d)
4. Se si sottrae da un numero intero il suo reciproco, si ottiene il doppio del numero intero che
lo precede. Qual è il numero in questione ?
a) 0
b) + 1
c) – 2
d) – 1
e) + 2
5. Una prova di ammissione è costituita da due test: il 45% dei candidati supera la prima prova
e solo 4/9 di quelli che hanno superato la prima prova supera anche la seconda. Su 180
candidati quanti saranno gli ammessi ?
a) 90
b) 30
c) 36
d) 40
e) 45
6. Le seguenti affermazioni:
• Il circocentro di un triangolo è sempre un punto interno al triangolo.
• L’ortocentro di un triangolo può essere un punto che appartiene al contorno del
triangolo.
• Il baricentro di un triangolo è sempre un punto interno al triangolo.
• L’incentro di un triangolo è un punto equidistante da tutti e tre i vertici del triangolo
Sono rispettivamente:
a) falsa, vera, falsa, falsa
b) falsa, vera, falsa, vera
c) vera, vera, vera, falsa
d) falsa, vera, vera, falsa
a) vera, vera, falsa, falsa
4a 2 − 4ab + b 2
, purché siano verificate le condizioni per la sua
2ab + 2a − b 2 − b
esistenza, è equivalente alla frazione:
2 − 2a
4a + 2b
2a − b
2a − b
b − 2a
a)
b)
c)
d)
e)
b
b −1
b −1
b +1
b −1
7. La seguente frazione:
8. Un animale ha una massa m1 = 40 kg; dopo 4 mesi, la sua massa, che indichiamo ora con
m2, è aumentata del 25% rispetto a m1. Dopo altri 4 mesi, la sua massa, che indichiamo ora
con m3, è aumentata del 20 % rispetto a m2; dopo un ulteriore aumento del 10%, la massa
finale è:
b) 66 kg
c) 60 kg
d) 58 kg
e) 68 kg
a) 70 kg
9. L’equazione (x – a) = (x – a)2 ammette:
a) una soluzione
b) nessuna soluzione
c) infinite soluzioni
d) due soluzioni
e) il numero delle soluzioni dipende da a
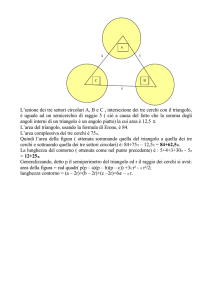
10. Due cerchi uguali sono tangenti esternamente.
Le quattro corde in figura sono uguali e
perpendicolari alla retta che unisce i centri
dei due cerchi. Se la distanza fra le due
corde più lontane dei due cerchi è 20 cm e
la distanza fra due corde dello stesso
cerchio è 8 cm, qual è l’area di uno dei due
cerchi?
b) 36π cm 2
c) 25π cm 2
d) 16π cm 2
a) 49π cm 2
e) Non è calcolabile perché non si conosce la lunghezza delle corde
11. In un triangolo isoscele la base e' uguale all'altezza ad essa relativa.
Si sa che sottraendo 10 m alla base ed aggiungendo 20 m all'altezza, l'area del triangolo
aumenta di 100 m2. Qual è l’area della superficie del triangolo ?
b) 200 m2
c) 600 m2
d) 900 m2
e) 800 m2
a) 400 m2
12. Quale delle seguenti affermazioni è corretta se riferita all’equazione (nell’incognita x)
2a 2b − 6ab x = a 3 − 3a 2
a) Se a = 0 l’equazione è impossibile
a
b) L’equazione è sempre determinata e la sua soluzione è x =
2b
c) Se a ∈ R − {0;3} e b ≠ 0 l’equazione è determinata
d) L’equazione ha sempre almeno una soluzione
e) Se b = 0 l’equazione è impossibile
(
)