Il controllo di sistemi ad avanzamento temporale si basa sulle tecniche
di controllo in retroazione, ovvero, elabora le informazione sullo stato
del processo (provenienti dai sensori) in modo sa inviare agli attuatori
le informazioni sulle azioni da compiere per imporre ad alcune
variabili un andamento desiderato specificato, su un intervallo
temporale finito o infinito, con una determinata precisione
La teoria classica del controllo, basandosi su una conoscenza del
modello del processo sotto forma di equazioni differenziali o alle
differenza, propone varie metodologie per effettuare la sintesi del
controllore
Sistemi ad avanzamento temporale - Controllo tempo continuo
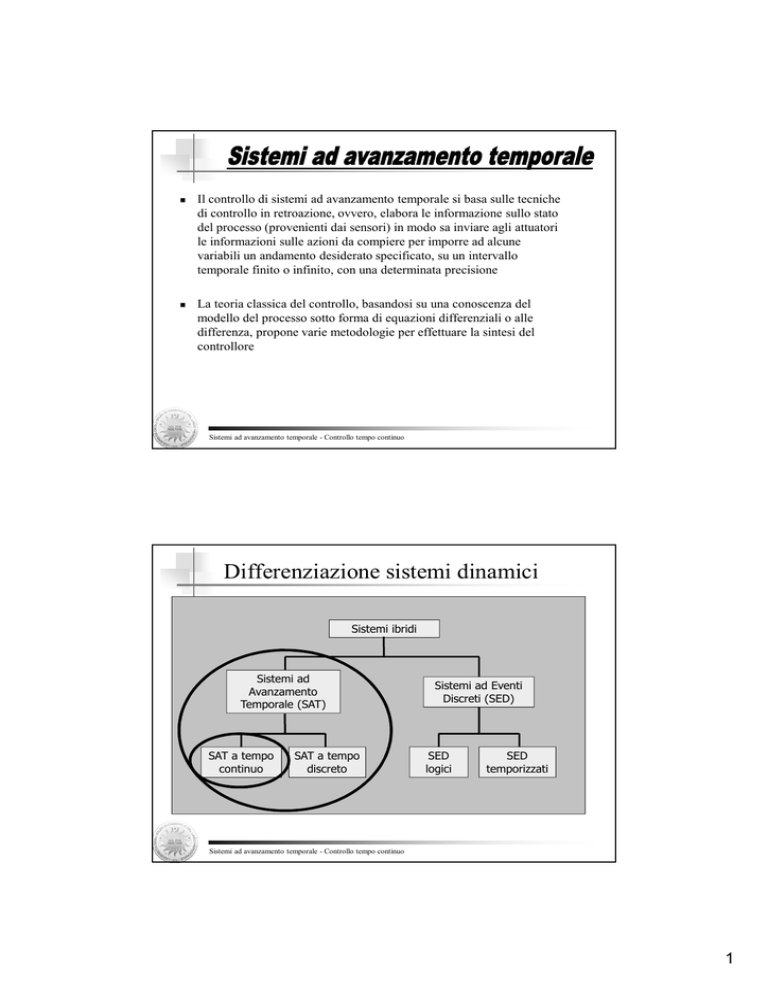
Differenziazione sistemi dinamici
Sistemi ibridi
Sistemi ad
Avanzamento
Temporale (SAT)
SAT a tempo
continuo
SAT a tempo
discreto
Sistemi ad Eventi
Discreti (SED)
SED
logici
SED
temporizzati
Sistemi ad avanzamento temporale - Controllo tempo continuo
1
Modello di sistema automatizzato
DISTURBI
ANDAMENTO
DESIDERATO
SISTEMA DI
CONTROLLO
ATTUATORI
PROCESSO
FISICO
SENSORI
Sistemi ad avanzamento temporale - Controllo tempo continuo
Esempi
Processo fisico Sensori
Attuatori
Sist. termici
Temperatura: termocoppie termoresistenze Generatori di calore
Sist. a fluido
Pressione: manometri a colonna,
estensimentri
Portata: dischi forati, sensori
elettromagnetici
Livello: principio idrostatico, capacitivo
Circuiti idraulici
Valv. di regolazione
Pompe
Sist. meccanici
Sensori di posizione/velocità: encoder
Sensori di accelerazione: accelerometri
Motori elettrici
Attuatori
oleodinamici
Sist. elettrici
Misure di corrente
Misure di tensione
Generatori di
corrente/tensione
Sistemi ad avanzamento temporale - Controllo tempo continuo
2
Richiami ai problemi di controllo
Obiettivo del controllo è quello di portare un sistema a comportarsi in
modo desiderato sulla base delle misure del suo stato attuale ed agendo
in modo opportuno.
L’oggetto del controllo è un sistema, detto impianto o processo, del
quale si vuole prefissare il comportamento in relazione ad un
opportuno insieme di dati di specifica.
Sistemi ad avanzamento temporale - Controllo tempo continuo
Richiami ai problemi di controllo
Ai fini del controllo di un impianto conviene distinguere le grandezze
di ingresso in due classi:
ingressi manipolabili — sono le grandezze mediante le quali è più agevole
influire sull’uscita;
ingressi non manipolabili — sono le grandezze che influenzano
l’andamento dell’uscita, ma non possono essere variate ad arbitrio.
Gli ingressi manipolabili sono quelli utilizzabili per il controllo, gli
ingressi non manipolabili giocano tipicamente il ruolo di grandezze di
disturbo del comportamento del sistema.
L’obiettivo viene espresso da un insieme di valori di riferimento di
certe variabili (variabili da controllare) mentre le azioni si effettuano
conferendo certi valori ad altre variabili (variabili di controllo)
Sistemi ad avanzamento temporale - Controllo tempo continuo
3
Modelli matematici
Il sistema viene descritto con l’ausilio di un modello matematico
desunto da leggi fisiche che ne esprimono il comportamento (e.g.
equazioni differenziali).
es. Sistema tempo continuo
lineare e stazionario
Altrimenti, un modello in forma discreta (e.g. equazioni alle
differenze) può essere ottenuto tramite identificazione parametrica a
partire da dati misurati
es. Sistema tempo discreto
lineare e stazionario
Sistemi ad avanzamento temporale - Controllo tempo continuo
Modelli matematici – Tempo Continuo
Modello Implicito Ingresso-Stato-Uscita per un sistema
SISO continuo e lineare
Modello Implicito Ingresso-Uscita per un sistema SISO
continuo e lineare
Sistemi ad avanzamento temporale - Controllo tempo continuo
4
Trasformata di Laplace
Trasformata di Laplace: permette di passare dal dominio del tempo al
dominio della variabile complessa s
Tempo
Laplace
Anti-trasformata di Laplace
Laplace
Tempo
Esempio: trasformata di Laplace della funzione esponenziale
Sistemi ad avanzamento temporale - Controllo tempo continuo
Trasformata di Laplace - Proprietà
Derivazione in t
Integrale in t
Il vantaggio più significativo della trasformata di Laplace è che
l'integrale e la derivata diventano una moltiplicazione e una divisione
rispettivamente
Teorema del valor finale
Sistemi ad avanzamento temporale - Controllo tempo continuo
5
Trasformata di Laplace-Sistema II° ordine
Sistema del 2° ordine nel dominio del tempo
Sistema del 2° ordine nel dominio di Laplace
Evoluzione libera
Evoluzione forzata
Sistemi ad avanzamento temporale - Controllo tempo continuo
Esempio
Sistema massa - molla - smorzamento
σ
m
f
k
x
Sistemi ad avanzamento temporale - Controllo tempo continuo
6
Risposta del sistema- Evoluzione libera
Risposta del sistema
Evoluzione libera
Poli
radici del polinomio caratteristico
Sistemi ad avanzamento temporale - Controllo tempo continuo
Modi di evoluzione
Modi di evoluzione con k = 0:
modi aperiodici
α >0
α =0
Il sistema risulta asintoticamente
stabile se tutti i poli hanno parte
reale negativa α<0
modi pseudoperiodici
α <0
α >0
α =0
α <0
Sistemi ad avanzamento temporale - Controllo tempo continuo
7
Modi di evoluzione
Costante di tempo associata al modo
Il modo di evoluzione si estingue in un tempo pari a 4-5
volte la sua costante di tempo
Sistemi ad avanzamento temporale - Controllo tempo continuo
Risposta del sistema- Evoluzione forzata
Risposta del sistema
Evoluzione forzata:
Risposta ad ingressi standard:
Risposta impulsiva
Risposta indiciale
Risposta ad ingressi polinomiali
Risposta ad ingressi sinusoidali (Bode, Nichols, Nyquist)
Sistemi ad avanzamento temporale - Controllo tempo continuo
8
Risposta indiciale
Risposta indiciale
W(s)
Sistemi ad avanzamento temporale - Controllo tempo continuo
Risposta indiciale
Risposta indiciale
Sistemi ad avanzamento temporale - Controllo tempo continuo
9
Caratteristiche della risposta
Regime (steady-state): situazione corrispondente all’equilibrio del
sistema
Transitorio: situazione temporanea di passaggio da uno stato di
equilibrio all’altro
Tempo morto: tempo necessario per osservare uno scostamento
significativo della variabile da controllare dalla banda di rumore in
seguito ad una variazione della variabile di controllo
Tempo di salita: tempo necessario perché la variabile da controllare si
sposti dal 10% al 90% del valore di regime
Tempo di assestamento: tempo necessario perché la variabile da
controllare rimanga prossima al set-point
Sovraelongazione: scostamento della variabile da controllare dal
setpoint
Sistemi ad avanzamento temporale - Controllo tempo continuo
Risposta armonica
Un generico segnale periodico u(t) di periodo T può essere
decomposto in serie di Fourier:
in cui
è la pulsazione fondamentale
Da ciò si evidenzia l’importanza di studiare la risposta del sistema ad
ingressi sinusoidali con diverse pulsazioni
Sistemi ad avanzamento temporale - Controllo tempo continuo
10
Risposta ad ingressi sinuisodali
Se il sistema ha tutti modi convergenti
a regime permanente l’uscita
del sistema sarà una sinusoide con la stessa pulsazione della sinusoide
di ingresso ma (generalmente) con diversa ampiezza e fase
Tale condizione si definisce di regime sinuisodale
W(s)
Sistemi ad avanzamento temporale - Controllo tempo continuo
Funzione di risposta armonica
valido qualunque sia ω
Nel caso di sistemi lineari e stazionari con modi di evoluzione
convergenti a zero, la funzione W(j ω) caratterizza completamente il
legame ingresso-uscita in condizioni di regime sinuisodale e viene
definita funzione di risposta armonica
Sistemi ad avanzamento temporale - Controllo tempo continuo
11
Diagramma di Bode
I diagrammi di Bode sono una coppia di grafici che rappresentano
l’andamento di modulo e fase in funzione della pulsazione (o frequenze)
della funzione di risposta armonica
I moduli sono
riportati in decibel
Le pulsazioni sono
in scala logaritmica
Sistemi ad avanzamento temporale - Controllo tempo continuo
Diagramma di Bode
La banda passante ωb rappresenta l’intervallo delle pulsazioni
all’interno del quale il contenuto spettrale di un segnale si trasmette
indistorto all’uscita
Il modulo di risonanza Mr è il
valore del picco di risonanza
normalizzato rispetto al
guadagno statico
Mr
ωb
Sistemi ad avanzamento temporale - Controllo tempo continuo
12
Legami globali
Banda passante ωb
Prontezza del sistema
Modulo di risonanza Mr
Sovraelongazione risposta indiciale
Mr
ω
b
Sistemi ad avanzamento temporale - Controllo tempo continuo
Obiettivi del sistema di controllo
Il controllore deve determinare (istante per istante) il valore da
attribuire alle variabili di controllo (u) in modo che l’andamento della
variabile da controllare (y) sia, malgrado l’influenza di disturbi
imprevedibili (d), il più possibile simile a quello desiderato (yd)
Un modo di classificare i sistemi di controllo riguarda l’andamento
dell’uscita desiderata yd. Rispetto ad esso si distinguono:
sistemi di regolazione: caratterizzati dall’avere un’uscita desiderata
costante
sistemi di asservimento: caratterizzati dall’avere un’uscita desiderata che
varia nel tempo
Sistemi ad avanzamento temporale - Controllo tempo continuo
13
Obiettivi del sistema di controllo
L’obiettivo del controllo potrebbe essere conseguito con una semplice
azione di compensazione statica in avanti, ma la presenza di una
retroazione (feedback) diviene indispensabile per contrastare gli effetti
degli ingressi non manipolabili, delle variazioni parametriche
sull’impianto e delle incertezze di modellazione
disturbi
Andamento
desiderato
legge di
controllo
organi di
comando
sistema da
controllare
misura
Sistemi ad avanzamento temporale - Controllo tempo continuo
Effetti della retroazione
Gli effetti della retroazione riguardano:
la sensibilità del sistema di controllo alle variazioni parametriche
dei suoi organi componenti
la sensibilità dell’uscita ai disturbi
la larghezza di banda del sistema
la capacità di linearizzare un legame ingresso uscita
la capacità di condizionare le caratteristiche prestazionali del
sistema
Sistemi ad avanzamento temporale - Controllo tempo continuo
14
Funzioni di trasferimento
Funzioni di trasferimento ingresso/uscita e disturbo/uscita:
C(s)P(s)
P(s)
G1(s)=
G2(s)=
1+C(s)P(s)H(s)
1+C(s)P(s)H(s)
d
e
yd
C(s)
u
P(s)
y
H(s)
Funzione di trasferimento ad anello aperto F(s)=C(s)P(s)H(s)
Sistemi ad avanzamento temporale - Controllo tempo continuo
Prestazioni e specifiche di controllo
Lo scopo del sistema di controllo è quello di portare a zero l’errore a
regime e di ottenere ciò nel minor tempo possibile, limitando gli
scostamenti della variabile controllata dal valore di riferimento e
cercando di contenere le oscillazioni (che si ripercuotono sugli organi
di comando)
Il sistema di controllo deve garantire una buona reiezione ai disturbi
La robustezza di una legge di controllo è una misura della capacità di
far fronte alle diverse condizioni di lavoro garantendo le prestazioni
desiderate
Sistemi ad avanzamento temporale - Controllo tempo continuo
15
Prestazioni e specifiche di regolazione
Prestazioni e specifiche chieste al sistema di controllo:
Stabilità: il regolatore deve smorzare le oscillazioni del processo e
costituire, insieme con esso, un sistema stabile ad anello chiuso
Errore nullo a regime: variabile di processo uguale al setpoint
Rapidità di risposta a variazioni di setpoint e disturbi: il regolatore
deve abbreviare i tempi di raggiungimento di equilibrio e
mantenerlo nonostante l’azione di disturbo
Limitate sovraelongazioni
Robustezza alle nonlinearità
Robustezza alle variazioni parametriche
Robustezza al rumore
Moderazione nelle variabili di controllo
Sistemi ad avanzamento temporale - Controllo tempo continuo
Precisione a regime
Ingressi canonici e tipo di sistema
Tipo di
sistema
0
1
2
gradino
er = cost
er =0
er = 0
rampa
lineare
er = ∞
er = cost
er = 0
rampa
parabolica
er = ∞
er = ∞
er = cost
La precisione a regime è determinata dal numero di poli
nell’origine e dalla costante di guadagno della funzione di
trasferimento di andata
Sistemi ad avanzamento temporale - Controllo tempo continuo
16
Errore regime: ingresso a gradino
kc,kp guadagni
statici di controllore
e processo
yd
e
C(s)
P(s)
y
-
Sistemi ad avanzamento temporale - Controllo tempo continuo
Precisione a regime
Ingressi canonici e tipo di sistema
Tipo di
sistema
0
gradino
rampa
lineare
er = ∞
rampa
parabolica
er = ∞
1
2
er =0
er = 0
er = 0
er = ∞
La precisione a regime è determinata dal numero di poli
nell’origine e dalla costante di guadagno della funzione di
trasferimento di andata
Sistemi ad avanzamento temporale - Controllo tempo continuo
17
Errore regime retroazione algebrica
R(s)=
R(s)
;
r
e
C(s)
P(s)
y
H0
Sistemi ad avanzamento temporale - Controllo tempo continuo
Errore regime retroazione algebrica
Per ingresso a gradino R
;
e
Per sistemi di tipo 0 (no poli origine tra C e P), a regime:
lim
lim
→
"# "$
→!
; lim
lim
→
r
e
"# "$
→!
C(s)
P(s)
y
H0
Sistemi ad avanzamento temporale - Controllo tempo continuo
18
Errore regime retroazione algebrica
Per ingresso a gradino R
;
e
Per sistemi di tipo 0 (no poli origine tra C e P), a regime:
lim
lim
→
"# "$
→!
;
lim
→
lim
"# "$
→!
Per sistemi di tipo 1 (un polo origine tra C e P), a regime:
lim
lim
→
%# %$
→!
=0
&
Sistemi ad avanzamento temporale - Controllo tempo continuo
Errore regime retroazione algebrica
Per ingresso a gradino R
'
'
e
;
'
Per sistemi di tipo 1 (un polo origine tra C e P), a regime:
lim
→
lim
&
'
lim
→
lim
→!
%( %$
'
→!
="
( "$
'
;
%( %$
&
"( "$
Sistemi ad avanzamento temporale - Controllo tempo continuo
19
Parametri caratteristici della risposta
Tempo morto: tempo necessario per osservare uno scostamento
significativo della variabile da controllare dalla banda di rumore in
seguito ad una variazione della variabile di controllo
Tempo di salita: tempo necessario perché la variabile da controllare si
sposti dal 10% al 90% del valore di regime
Tempo di assestamento: tempo necessario perché la variabile da
controllare rimanga prossima al set-point
Sovraelongazione: scostamento della variabile da controllare dal
setpoint
Sistemi ad avanzamento temporale - Controllo tempo continuo
Risposta a gradino unitario
Risposta a gradino unitario
Sistemi ad avanzamento temporale - Controllo tempo continuo
20
Criteri di stabilità per sistemi in retroazione
Una delle principali proprietà richieste ad un sistema di controllo è la
stabilità asintotica; essa infatti è premessa necessaria per il
conseguimento di una condizione di funzionamento in regime
permanente nella quale valutare la precisione mostrata nell’inseguire il
riferimento imposto e/o la capacità di reiezione di disturbi permanenti
la stabilità del sistema ad anello chiuso dipende dall’analisi della
funzione razionale fratta 1+F(s) (dove F(s) è la funzione trasferimento
ad anello aperto)
G1(s) =
C(s)P(s)
= C(s)P(s)
1+C(s)P(s)H(s)
1+F(s)
In particolare le soluzioni di
1+F(s)=0
devono essere tutte con parte reale negativa per garantire la stabilità
asintotica del sistema in retroazione
Sistemi ad avanzamento temporale - Controllo tempo continuo
Criteri di stabilità per sistemi in retroazione
Il criterio di Routh consente di analizzare le proprietà di stabilità di un
sistema dinamico lineare e stazionario mediante la costruzione di una
tabella che fornisce indicazione sul numero di radici a parte reale
negativa, nulla, e positiva del polinomio caratteristico senza richiedere
la soluzione dell’equazione caratteristica.
Il criterio di Nyquist è basato sull’analisi dell’andamento del
diagramma di Nyquist della funzione di trasferimento ad anello aperto,
F(s), valutata per s=jω.
“Un sistema in retroazione è asintoticamente stabile se e solo se il
vettore rappresentativo del numero complesso 1+F(jω)al variare di ω
da -∞ a +∞ compie intorno al proprio punto di applicazione un
numero di giri, valutati positivamente in verso antiorario, pari al
numero di poli a parte reale positiva della funzione di trasferimento ad
anello aperto”
Sistemi ad avanzamento temporale - Controllo tempo continuo
21
Margini di fase e guadagno
Il margine di fase cambiato di segno è il valore della diminuzione di
fase che forza il sistema ad anello chiuso ad avere poli immaginari
coniugati (limite di stabilità).
Il margine di guadagno è l’inverso del modulo di F(jω) quando il suo
diagramma polare attraversa l’asse delle ascisse.
Sistemi ad avanzamento temporale - Controllo tempo continuo
Sintesi del controllore
C(s) =
K (1+α s)
sr (1+β s)
Guadagno statico (rapidità sistema e precisione a regime er ≠ 0 )
Numero poli nell’origine (precisione a regime er=0)
Rete correttrice (stabilità e specifiche del transitorio)
d
yd
e
C(s)
u
P(s)
y
H(s)
Sistemi ad avanzamento temporale - Controllo tempo continuo
22
Metodi di sintesi del controllore
Metodi per tentativi
Risposta in frequenza (basati su relazione F(jω) -- W(jω)
es. Carte di Nichols )
Luogo delle radici (basati su relazione F(s)--W (s))
Metodi empirici (es. regolatori standard)
Metodi diretti
cancellazione ed allocazione poli
Sistemi ad avanzamento temporale - Controllo tempo continuo
Sintesi del controllore
C(s) =
K (1+α s)
sr (1+β s)
Numero poli nell’origine in base al tipo di sistema desiderato
Guadagno statico in base all’errore a regime
Rete correttrice in base a specifiche relative al transitorio (spesso
espresse tramite legami globali in termini di pulsazione di
attraversamento e margini di fase)
d
yd
e
C(s)
u
P(s)
y
H(s)
Sistemi ad avanzamento temporale - Controllo tempo continuo
23
Formule per reti correttrici
Rete anticipatrice
Rete ritardatrice
Sistemi ad avanzamento temporale - Controllo tempo continuo
24











