16. Sostituzione di variabile: attenzione a cattura

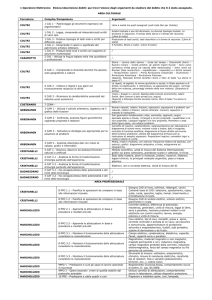
16. Sostituzione di variabile: attenzione a cattura variabili!
Definizione di sostituzione di un termine Dato un termine t di un linguaggio predicativo e una
formula pr(x) allora indichiamo con pr[x/t] la formula ottenuta sostuendo x con t in pr(x). Tale formula
è definita come segue:
Pk (t1 , . . . , tm )[x/t]
 ≡ Pk (t1 [x/t], . . . , tm [x/t])
∀yi pr[x/t] se yi 6= x e x compare in pr

(∀yi pr)[x/t] ≡
e yi NON compare libera in t


se yi ≡ x o x non compare in pr
∀yi pr

∃y
pr[x/t]
se
yi 6= x e x compare in pr
 i
(∃yi pr)[x/t] ≡
e yi NON compare libera in t


∃yi pr
se yi ≡ x o x non compare in pr
(pr1 & pr2 )[x/t] ≡ pr1 [x/t] & pr2 [x/t]
(pr1 ∨ pr2 )[x/t] ≡ pr1 [x/t] ∨ pr2 [x/t]
(pr1 → pr2 )[x/t] ≡ pr1 [x/t] → pr2 [x/t]
(¬pr1 )[x/t] ≡ ¬pr1 [x/t]
MORALE
Quando sostituisci una variabile y al posto di x in un predicato pr(x)
controlla che - SE compare ∀y o ∃y in pr(x) la sostituzione di x con y NON faccia cadere il nuovo y
sotto il POTERE di ∀y o ∃y
ovvero aumenti il numero di occorrenze di y in loro potere!
∃y y = y ` ∇
∀−S
∀x ∃y x = y ` ∇
∀y y = a ` y = z
∀−D
∀y y = a ` ∀x x = z
NOOOOO!!!!
SI!!!!
Stabilire quali delle seguenti applicazioni di ∀-S o ∃-D sono lecite
1. È lecita la seguente applicazione di ∀-S
∀y ∃x x < y + z ,
∃x x < x + z ` ∇
∀−S
∀y ∃x x < y + z ` ∇
??
2. È lecita la seguente applicazione di ∀-S
∀y ∃x x < y + z ,
∃x x < z + z ` ∇
∀−S
∀y ∃x x < y + z ` ∇
??
3. È lecita la seguente applicazione di ∀-D
1
Γ ` ∃x x < z + z
∀−D
Γ ` ∀y ∃x x < y + z
??
4. È lecita la seguente applicazione di ∀-D
Γ ` ∃x x < x + z
∀−D
Γ ` ∀y ∃x x < y + z
??
5. È lecita la seguente applicazione di ∀-D
∀y C(y) ` ∃x x < y + z
∀−D
∀y C(y) ` ∀w ∃x x < w + z
??
Esercizi su uguaglianza
1. Nell’estensione di LC con uguaglianza, ovvero in LC= , stabilire se sono validi o meno, o soddisfacibili o meno i seguenti sequenti:
(a) ` ¬∀x x = x
(b) `∀y ∀x x=y
(c) ` ∀y ∀x ∀z ( x = y & z = y → x = z )
(d) ` ∃x ∃y x = y
(e) ` ∀x ∃y ∃z ( x = y ∨ y = z )
(f) ∀w w = a ` ∀x ∀y x = y
2. Formalizzare l’ asserzione
Franco è venuto ad una sola riunione.
Franco non è venuto all’ultima riunione.
Franco è venuto alla riunione del 10 giugno.
L’ultima riunione non è quella del 10 giugno.
utilizzando:
V(x,y)= x è venuto alla riunione y
u=ultima riunione
d=riunione del 10 giugno
f=Franco
2
Paradosso Russell e curiosa verità
1. È vero che in questa aula
“C’è un tale che se lui ride allora tutti ridono.”
??
Formalizzare con
R(x)= “x ride”
2. È vero che in questa aula
“C’è un tale che se lui vota contro l’uso del tablet a lezione allora tutti votano contro l’uso del
tablet a lezione .”
??
Formalizzare con
V (x)= “x vota contro l’uso del tablet a lezione”
Stabilire se la formula ottenuta è valida o meno e soddisfacibile o meno in logica classica.
3. come si formalizza
“Esiste uno che rade tutti quelli che non radono se stessi.”
??
si consiglia di usare:
R(x,y)=“x rade y”
4. come si formalizza
“Esiste uno che rade soltanto quelli che non radono se stessi.”
??
Poi stabilirne la validità e soddisfacibilità o meno in logica classica.
5. come si formalizza
“Esiste uno che rade tutti quelli che non radono se stessi e soltanto loro.”
??
Poi stabilirne la validità e soddisfacibilità o meno in logica classica.
3