Alcune proprietà fenomenologiche dei semiconduttori

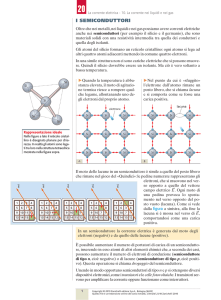
Alcune proprietà fenomenologiche dei semiconduttori
1. Sono caratterizzati da una banda di energia proibita (energy gap) che vale
approssimativamente 0,7 eV per il Ge, 1,12 eV per il Silicio, 1,43 per il GaAs per
citare i tre semiconduttori più importanti dal punto di vista applicativo e storico. Se la gap,
per un dato semiconduttore, è proibita, non possono esistere nel semiconduttore stesso
portatori di carica con energia i cui valori cadono all’interno di detta gap.
2. La conducibilità S dei semiconduttori cresce con la temperatura, cioè T
s . Nei
metalli si verifica che se T
s
3. Le proprietà elettroottiche dei semiconduttori sono ben circoscritte per quanto riguarda lo
stato cristallino; per lo stato amorfo e policristallino tali proprietà sono sufficientemente
conosciute.
4. Se si considera una barra di semiconduttori a cui venga applicata una d.d.p., la
distribuzione di detto potenziale risulta lineare e come conseguenza, nell’ipotesi di
assenza di regioni di carica spaziale, la densità di carica risulta nulla, cioè la densità delle
cariche mobili è bilanciata da quelle fisse. Infatti dalla formula
2
V
0
V
discende che, se V ha andamento lineare lungo la barra,
0.
5. Dato un semiconduttore sottoposto ad una d.d.p., la corrente I misurata può essere dovuta
o ad un flusso di cariche positive che procedono con velocità di trasporto up diretta nel
verso del campo elettrico, oppure da un flusso di cariche negative che procedono con
velocità un diretta in verso opposto. Le velocità sono da intendersi velocità medie; le
cariche negative (elettroni) viaggiano con energie tipiche della banda di conduzione; le
cariche positive (lacune) viaggiano con energie tipiche della banda di valenza. Quindi,
dato un campo E, le up ed un per quanto riguarda i versi sono quelle disegnate in figura 1,
essendo la forza F = q E.
E
up
+
un
-
Figura 1 – Direzione e verso delle velocità di elettroni e lacune rispetto al campo elettrico E
La densità di corrente J [A/m 2] può essere espressa in due modi:
J
u
J
E
o
m
3
dove m è la densità di carica [Q/cm ], u è la velocità [m/s],
[( cm) -1 ]ed il campo elettrico [V/cm].
1
è la conducibilità
Indicando con p la concentrazione di carica positiva [cm-3 ] e con n la concentrazione di
carica negativa [cm-3 ], nell’ipotesi di un solo portatore presente nel semiconduttore si ha:
q p
q n (per gli elettroni)
(per le lacune)
m
m
Come conseguenza le densità di corrente J si possono scrivere:
Jp
q p up
Jn
q n un
Jp
p
E
Jn
n
E
p
E
q
p
up
n
un
q
1
E
1
E
E
E
Inoltre:
up
up
E
n
dove p e n sono le mobilità delle lacune e degli elettroni, rispettivamente.
Le mobilità sono espresse da numeri positivi, cioè
up
un
p
n
E
Dalle relazioni precedenti si ha:
Jp
E
q p
p
p
E
Jn
E
n
E
Quindi per quanto attiene le conducibilità (quantità positive) si ha:
q p
q n
p
p
n
q
n
n
E
n
Nel caso in cui, in un dato semiconduttore gli elettroni coesistano con le lacune si può
dimostrare che la conducibilità totale è data dalla seguente espressione cumulativa:
q
p
n
tot
p
n
Diffusione
L’effetto diffusivo, in assenza di forze che lo contrastino, produce un flusso di particelle in
direzione ortogonale alla superficie di eguale concentrazione delle particelle stesse.
Tale flusso procede dalle alte alle basse concentrazioni e con intensità legata al livello del
gradiente.
Indicando con p e con n le densità di flusso rispettivamente di lacune e di elettroni si può
scrivere che:
p
Dp
grad(p)
n
Dn
grad(n)
dove:
2
Dp
Lp
Dn
p
L2n
n
sono i coefficienti di diffusione, Ln e Lp sono le lunghezze medie di diffusione per elettroni e
lacune e n e p sono i tempi medi tra urti per elettroni e lacune e ricordando che
Dp
Dn
cm 2
sec
2
Importanti relazioni (Relazioni di Einstein) legano i coefficienti di diffusione alle mobilità.
K T
K T
Dp
Dn
p
n
q
q
dove T è la temperatura assoluta e K è la costante di Boltzman (1,35 10-23 [J/h]).
Inoltre:
Valori tipici per T = 300°K del coefficiente di
diffusione per elettroni e lacune del Si e del Ge
Dp
Dn
p
n
VT
T
11.600
Dn =
Dp =
35 cm2/sec
13 cm2/sec
(Si)
(Si)
Dn =
Dp =
100 cm2/sec
50 cm2/sec
(Ge)
(Ge)
Moltiplicando i flussi n e p per la carica degli elettroni e delle lacune si ottengono le
densità di corrente Jn e Jp:
Jp
q D p grad p
Jn
q Dn grad n
p
Jp ,
n
p
n
Jn
p , Jp
n
Jn
x
Figura 2 – Flussi
x
e densità di corrente J per due funzioni di concentrazione
Poiché in generale gli effetti chimico e diffusivo coesistono in un semiconduttore, la legge più
semplice atta a governare il movimento delle cariche riguarda la combinazione dei due
termini, uno di drift, dipendente dal campo, l’altro di diffusione, dipendente dal gradiente di
concentrazione. Quindi le due espressioni della densità di corrente di lacune ed elettroni si
scrivono nel seguente modo:
Jp
q p
E q Dp grad p
p
Jn
q n
E q Dn grad n
n
con Jtot
Jp
Jn .
Le due equazioni precedenti che esprimono Jp e Jn sono dette Equazioni del trasporto.
3
Altre relazioni sono importanti e necessarie per descrivere il comportamento delle cariche in
un semiconduttore; ma di queste una può essere derivata considerando il bilancio di
conservazione dei portatori di carica. Tale relazione prende il nome di Equazione di
continuità.
Equazione di continuità
Si consideri un volume V, delimitato dalla superficie S, contenente lacune con densità p
Il numero totale di lacune nel volume dato può
essere espresso come segue:
a
P
p
dV
V
e la variazione di P nel tempo è data da:
dP
d
Ä lacune
p dV
dt
dt V
V
S
Tale variazione può essere dovuta ad un flusso uscente o entrante, di cariche più ad una
variazione, nel processo di generazione-ricombinazione.
Sia allora:
G = n° di coppie generate nell’unità di volume e nell’unità di tempo
R = n° di coppie che si ricombinano nell’unità di volume e nell’unità di tempo
a = versore normale ad S
allora si può scrivere:
d
p dV
dt V
dove
R
dV
a
p
dS
S
Jp q
p
V
G
V
d
p
dt
dV
R
G
1
q
dV
V
div J p
dV
S
che si può anche scrivere:
V
d p
dt
(R
1
q
G)
div J p
dV
0
se si suppone che tale relazione possa valere per ogni V, ed anche per dV, si ha:
d p
dt
(R
G)
Ora si ponga G
termico. Quindi R
R
G
Gth
G
U
1
q
div J p
0
G dove per G’ si considera ogni effetto diffusivo diverso dal
R
G th
G e considerando U
R
Gth si ha:
G
4
Con tali posizioni si può scrivere
p
1
U
div J p
t
q
n
1
U
div J n
t
q
G
G
Moltiplicando per q e –q e sommando si ottiene:
ñ
div J
0
t
Per quanto attiene il campo elettrico si ha:
E r, t
grad r, t
Inoltre si deve considerare il legame tra
e
compreso nell’Equazione di Poisson seguente:
2
t
q
dove
ND
NA
p
n .
Ricapitolazione
Formiamo il quadro completo delle equazioni in grado di determinare il comportamento dei
dispositivi, almeno fino a quando i campi elettrici consentono di restare in un sistema di
riferimento governato dalla linearità.
Trasporto:
Jp
Jn
Continuità:
p
t
n
t
q
p
p
E
q
Dp
grad p
q
n
n
E
q
Dn
grad n
1
q
1
q
U
U
div J p
G
div J n
G
Poisson:
2
0
r
Quasi stazionarietà:
E
grad
Densità di carica totale
q ND
NA
p
n
5