Esercizi per la prova scritta
Disequazioni + Geometria 1
1. La disequazione – ݔ > ݔha per soluzione:
–; ݔ > ݔ
Soluzione
ሿ−∞, 0ሾ
− ݔ− > ݔ0 ;
−2 > ݔ0 ;
2 < ݔ0 ;
0
−∞
<ݔ0
+∞
2. La disequazione ሺ ݔ− 1ሻଶ + 9ݔሺ ݔ− 1ሻ > ݔଶ − 4 ݔ+ 4 − ሺ1 + 3ݔሻሺ1 − 3ݔሻ ha per soluzione:
ሺ ݔ− 1ሻଶ + 9ݔሺ ݔ− 1ሻ > ݔଶ − 4 ݔ+ 4 − ሺ1 + 3ݔሻሺ1 − 3ݔሻ ;
Soluzione
ݔଶ + 1 − 2 ݔ+ 9 ݔଶ − 9 ݔ > ݔଶ − 4 ݔ+ 4 − ሺ1 − 9 ݔଶ ሻ ;
+1 − 2 ݔ− 9 > ݔ−4 ݔ+ 4 − 1 ;
−2 ݔ− 9 ݔ+ 4 > ݔ+4 − 1 − 1 ;
−7 > ݔ+2 ;
7 < ݔ−2 ;
2
<ݔ− .
7
−∞
−
2
൨−∞, −
7
2
7
+∞
ݔ− 2 ݔ− 1 3 ݔ+ 1
1
−
≥
− 2 ൬ ݔ+ ൰
4
2
3
6
Soluzione
3. Qual è la soluzione della disequazione:
ݔ− 2 ݔ− 1 3 ݔ+ 1
1
−
≥
− 2 ݔ− ;
4
2
3
3
ݔ−2
ݔ−1
3 ݔ+ 1
1
12 ∙
− 12 ∙
≥ 12 ∙
− 12 ∙ 2 ݔ− 12 ∙ ;
4
2
3
3
3ሺ ݔ− 2ሻ − 6ሺ ݔ− 1ሻ ≥ 4ሺ3 ݔ+ 1ሻ − 24 ݔ− 4 ;
3 ݔ− 6 − 6 ݔ+ 6 ≥ 12 ݔ+ 4 − 24 ݔ− 4 ;
3 ݔ− 6 ݔ− 12 ݔ+ 24 ≥ ݔ0 ;
9 ≥ ݔ0 ;
≥ݔ0 ;
ሾ0, +∞ሾ
−∞
0
+∞
4.
ݔ−2
≤0
ݔ+1
ݔ−2≥0
ݔ+1>0
ܰ
ܦ
−4 ݔ+ 2 ≤ ݔ3 + 2
൝
2 ݔ+ 27 > 3 ݔ+ 18
5. Risolvi il seguente sistema di disequazioni:
5
≥ݔ−
2
൞
−
ܦ
> ݔ−1
−4 ݔ− 2 ≤ −2 ݔ+ 3
൝2
ݔ+9 > ݔ+6
3
−
ܰ
≥ ݔ+2
<ݔ9
5
− ≤<ݔ9
2
−∞
−
−1
+
+
5
2
9
5
2
9
−
≤ ݔ−1 ∨ > ݔ0
ۓ
ۖ
−2 < < ݔ0 ∨ 0 < < ݔ2
۔
ۖ
> ݔە0
+
−
−2 ≤ ݔ5
൝
2 ݔ− 3 > ݔ18 − 27
−
+
2
+
൝
2 ≥ ݔ−5
− > ݔ−9
+∞
5
− , 9
2
6. Risolvi il seguente sistema di disequazioni :
ݔۓ+ 1
ۖ ଷ ≥0
ݔ
ݔ ۔ସ − 4 ݔଶ < 0
ۖ2 ݔଷ > 0
ە
Matematica
www.mimmocorrado.it
ሾ0 < < ݔ2ሿ
2
1. In una fabbrica di giocattoli, si producono pupazzi che vengono rivenduti a € 7,00 ciascuno. Sapendo che i costi
fissi mensili (affitto, luce, acqua, stipendi, ecc.) ammontano a € 2100,00 e che il costo del materiale per ogni
pupazzo è di €3,50, determina quanti pupazzi devono essere prodotti mensilmente affinché il bilancio non vada
in perdita. Se la fabbrica riuscisse a produrre soltanto 500 pupazzi al mese, quanto dovrebbe essere il prezzo di
rivendita di un pupazzo affinché il bilancio non vada in perdita.
(Risolvi il problema sia algebricamente sia graficamente)
Soluzione
݊ݔ = ݅ݖݖܽݑ ݅݁݀ ݎ݁݉ݑ
Ponendo:
ܴ݅ܿܽݐݏܥ ≥ ݒ
7 ≥ ݔ2100 + 3,5; ݔ
si ha:
14 ≥ ݔ4200 + 7; ݔ
14 ݔ− 7 ≥ ݔ4200 ;
7 ≥ ݔ4200
≥ ݔ600 .
Pertanto, affinché il bilancio non vada in perdita, la fabbrica deve produrre almeno 600 pupazzi al mese.
Punto di pareggio
Matematica
www.mimmocorrado.it
3
ܲݖ = ݖݖܽݑ ݊ݑ ݅݀ ݖݖ݁ݎ
Ponendo:
ܴ݅ܿܽݐݏܥ ≥ ݒ
500 ≥ ݖ2100 + 3,5 ∙ 500 ;
si ha:
500 ≥ ݖ2100 + 1750 ;
500 ≥ ݖ3850 ;
≥ ݖ7,7
Pertanto, se la fabbrica riuscisse a produrre soltanto 500 pupazzi al mese, affinché il bilancio non vada in
perdita, il prezzo di rivendita di un pupazzo dovrebbe essere almeno di €7,70 .
Punto di pareggio
Matematica
www.mimmocorrado.it
4
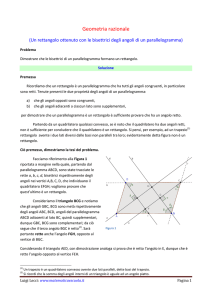
1. Dimostra che la somma degli angoli esterni di un quadrilatero è congruente a un angolo giro.
Dimostrazione
La diagonale del quadrilatero
quadrilatero in due triangoli.
divide
il
Essendo la somma degli angoli interni di un
triangolo congruente a un angolo piatto, si ha che
la somma degli angoli interni del quadrilatero è
congruente a 2 angoli piatti.
Inoltre, come si evince dal grafico, la somma di un
qualsiasi angolo esterno con l’angolo interno ad
esso adiacente è congruente a un angolo piatto.
Pertanto la somma di tutti gli angoli interni e di
tutti gli angoli esterni del quadrilatero è pari a 4
angoli piatti.
Si conclude perciò, che la somma degli angoli
esterni di un quadrilatero è congruente a 2 angoli
piatti, cioè a un angolo giro.
concavo. Dimostra che l’angolo convesso AD
C è
2. Considera un quadrilatero concavo ABCD avente l’angolo D
congruente alla somma degli angoli A , B , C del quadrilatero.
Dimostrazione
Tracciamo la retta BD.
Consideriamo il triangolo ABD.
Ricordando che la somma degli angoli interni di
un triangolo è 180°, si ha:
ܤ
ܣ + ܤܣ ≅ ܦ180° − ܦܣ
≅ ܧ180° − ܦܣ
ܤ
Ma ܦܣ
E ≅ A + AB
D
Pertanto: AD
ܥ
ܥ + ܤܦ ≅ ܥ180° − ܦܤ
Consideriamo il triangolo BDC.
≅ ܥ180° − ܦܤ
ܥ
Ma ܦܧ
ܥ ≅ ܥ + ܤܦܥ
Pertanto: ܦܧ
≅ ܥAD
E + ܦܧ
≅ ܥA + AB
D + ܥ + ܤܦ ≅ ܥA + B
+ ܥ .
ܦܣ
Si conclude quindi che l’angolo convesso:
Matematica
www.mimmocorrado.it
5
3. Dimostra che in un trapezio isoscele gli angoli adiacenti a ciascuna base sono congruenti.
Dimostrazione
I due triangoli ADH e BCK sono congruenti per il IV C.C.T.R.
Infatti:
AD ≅ BC per ipotesi
ܭܥ ≅ ܪܦperché altezze del trapezio
Pertanto gli angoli ܣመ e ܤ adiacenti alla base maggiore
sono congruenti.
e ܥመ adiacenti alla base minore sono
Anche gli angoli ܦ
congruenti, perché somma di angoli congruenti.
Infatti:
ܥܭ ≅ ܪመ ܤper la dimostrazione precedente.
ܦܣ
ܥܦ ≅ ܥመ ≅ ܭ90° perché le altezze sono perpendicolari alle basi.
ܦܪ
4. Dimostra che, in un trapezio isoscele in cui i lati obliqui sono congruenti alla base minore, le diagonali sono
bisettrici degli angoli adiacenti alla base maggiore.
Ipotesi
ܦܥܤܣè un trapezio isoscele
ܥܤ ≅ ܥܦ ≅ ܦܣ
Tesi
ܣܥመܣܤ ≅ ܦመܥ
ܤܣܤܥ ≅ ܦܦ
⇒
Dimostrazione
ܣܥመܥܣ ≅ ܦመ ܦperché ܦܥܣè un triangolo isoscele.
ܥܣመ ܣܥ ≅ ܦመ ܤperché angoli alterni interni
Per la proprietà transitiva si ha: ܣܥመܣܥ ≅ ܦመܤ
In modo analogo si dimostra l’altra parte della tesi.
5. Sia O il punto di intersezione delle diagonali di un parallelogramma ABCD. Traccia una retta r passante per O e
indica con P il suo punto di intersezione con il lato AB e con Q il suo punto di intersezione con il lato CD. Dimostra
che O è il punto medio dei PQ.
Ipotesi
ܦܥܤܣè un parallelogramma
O è il punto di incontro delle
diagonali
Tesi
⇒
OP≅ ܱܳ
Dimostrazione
I triangoli ܱ ܲܤܱ ≅ ܳܦper il II C.C.T. Infatti:
ܱܦܳ ≅ ܱܲ ܤperché opposti al vertice
ܱ ܤܱ ≅ ܦperché le diagonali si incontrano nel loro punto medio
ܳ ≅ ܲܤܱ perché alterni interni
ܱܦ
Pertanto si conclude che: OP≅ ܱܳ .
Matematica
www.mimmocorrado.it
6
6. In un parallelogramma ABCD, sia M il punto medio di AD ed N il punto medio di BC. Dimostra che:
a. AN E MC sono paralleli
Ipotesi
ܦܥܤܣè un
parallelogramma
ܦܯ ≅ ܯܣ
ܥܰ ≅ ܰܤ
Tesi
⇒
ܥܯ ∥ ܰܣ
Dimostrazione
Ricordando il teorema: “Se un quadrilatero ha due lati opposti congruenti e paralleli, allora è un
parallelogramma”, si ha che: ܯܥܰܣè un parallelogramma.
Infatti:
ଵ
ଵ
Essendo ABCD un parallelogramma, si ha che: ܥܤ ≅ ܦܣe conseguentemente: ≅ ܯܣଶ ≅ ܦܣଶ ; ܰܥ ≅ ܥܤ
mentre ܥܰ ∥ ܯܣperché segmenti appartenenti ai lati opposti ܥܤ ݁ ܦܣdel parallelogramma.
Essendo ܯܥܰܣun parallelogramma, si conclude che: ܥܯ ∥ ܰܣ.
Matematica
www.mimmocorrado.it
7