Geometria razionale

Geometria razionale
(Un rettangolo ottenuto con le bisettrici degli angoli di un parallelogramma)
Problema
Dimostrare che le bisettrici di un parallelogramma formano un rettangolo.
Soluzione
Premessa
Ricordiamo che un rettangolo è un parallelogramma che ha tutti gli angoli congruenti, in particolare
sono retti. Tenute presenti le due proprietà degli angoli di un parallelogramma:
a)
b)
che gli angoli opposti sono congruenti,
che gli angoli adiacenti a ciascun lato sono supplementari,
per dimostrare che un parallelogramma è un rettangolo è sufficiente provare che ha un angolo retto.
Partendo da un quadrilatero qualsiasi convesso, se è noto che il quadrilatero ha due angoli retti,
non è sufficiente per concludere che il quadrilatero è un rettangolo. Si pensi, per esempio, ad un trapezio(1)
rettangolo avente i due lati diversi dalle basi non paralleli tra loro; evidentemente detta figura non è un
rettangolo.
Ciò premesso, dimostriamo la tesi del problema.
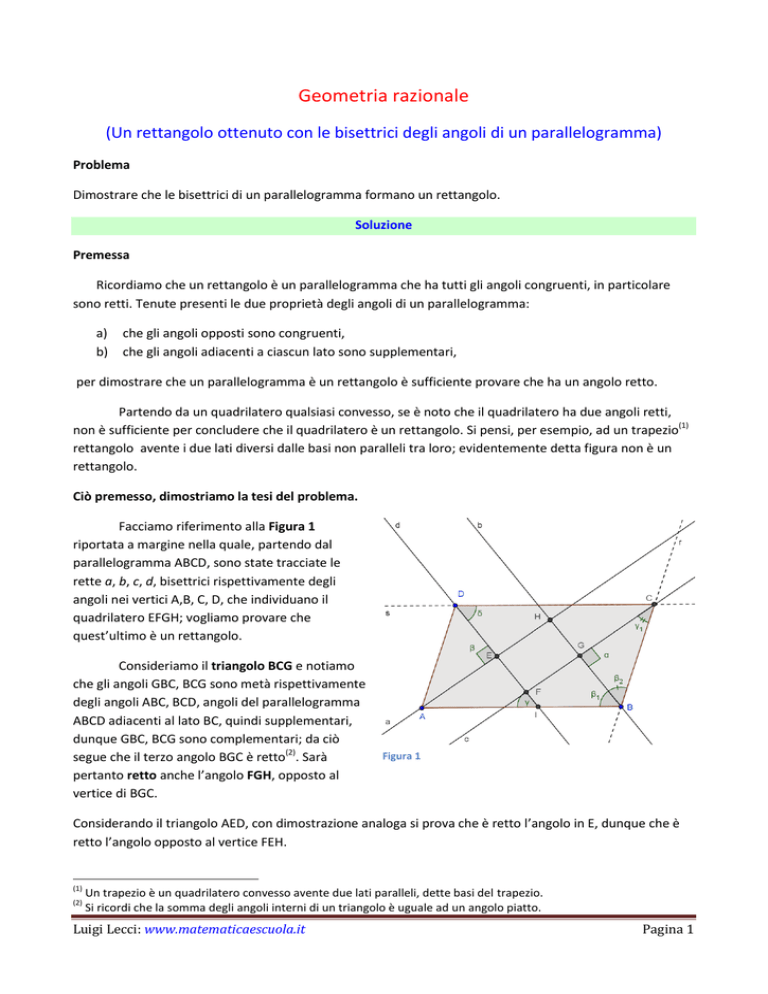
Facciamo riferimento alla Figura 1
riportata a margine nella quale, partendo dal
parallelogramma ABCD, sono state tracciate le
rette a, b, c, d, bisettrici rispettivamente degli
angoli nei vertici A,B, C, D, che individuano il
quadrilatero EFGH; vogliamo provare che
quest’ultimo è un rettangolo.
Consideriamo il triangolo BCG e notiamo
che gli angoli GBC, BCG sono metà rispettivamente
degli angoli ABC, BCD, angoli del parallelogramma
ABCD adiacenti al lato BC, quindi supplementari,
dunque GBC, BCG sono complementari; da ciò
segue che il terzo angolo BGC è retto(2). Sarà
pertanto retto anche l’angolo FGH, opposto al
vertice di BGC.
Figura 1
Considerando il triangolo AED, con dimostrazione analoga si prova che è retto l’angolo in E, dunque che è
retto l’angolo opposto al vertice FEH.
(1)
(2)
Un trapezio è un quadrilatero convesso avente due lati paralleli, dette basi del trapezio.
Si ricordi che la somma degli angoli interni di un triangolo è uguale ad un angolo piatto.
Luigi Lecci: www.matematicaescuola.it
Pagina 1
Abbiamo così acquisito che il quadrilatero EFGH ha due angoli retti. Ciò non è sufficiente ancora per
affermare che si tratta di un rettangolo.
Proviamo che i lati EF, GH sono tra loro paralleli.
I due segmenti giacciono rispettivamente sulle rette d (bisettrice di ADC), b (bisettrice di ABC).
Ricordato che gli angoli opposti in un parallelogramma sono congruenti si deduce che sono congruenti tra
loro gli angoli ABG, CDE. D’altra parte, la retta d interseca le rette dei lati paralleli AB, CD formando in
particolare la coppia di angoli AID, CDI alterni interni, quindi questi ultimi sono congruenti e da ciò segue,
per transitività, che AIDABG, dunque le rette b, d, sono tra loro congruenti perché tagliate dalla
trasversale AB formano la coppia di angoli corrispondenti AID, ABG congruenti.
Verso la conclusione
Avendo precisato che l’angolo FGH è retto, quindi che la retta bc, deduciamo che cd poiché d//b e
quindi anche l’angolo EFG è retto. A questo punto sappiamo che il quadrilatero EFGH ha tre angoli retti e
possiamo concludere che è un rettangolo. C.V.D.
Osservazione
Modificando la forma del parallelogramma ABCD si
deforma il quadrilatero convesso EFGH perché i
suoi vertici cambiano posizione. A margine, in
Figura 2, è illustrata un’altra situazione
geometrica. Il lettore può utilizzare questa seconda
figura per dimostrare la tesi enunciata nel
problema.
Figura 2
Luigi Lecci: www.matematicaescuola.it
Pagina 2