Il MOSFET

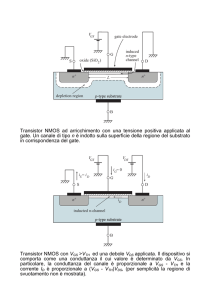
Il MOSFET
Si può ottenere un altro tipo di dispositivo a effetto di campo utilizzando
un elettrodo metallico (gate) separato mediante uno strato di ossido dal
canale di materiale semiconduttore. La struttura metallo-ossidosemiconduttore (MOS) consente di controllare le caratteristiche conduttive del canale mediante un campo elettrico, ottenuto applicando una
differenza di potenziale tra il gate e massa che si trasmette attraverso lo
strato di ossido. Il transistore così realizzato è chiamato MOSFET.
Esistono due tipi di MOSFET: ad arricchimento (E-MOSFET) e a
svuotamento (D-MOSFET), dipendentemente dalla modalità di
realizzazione del canale. Il D-MOSFET ha un comportamento molto
simile a quello del JFET: per una tensione di gate nulla e per una tensione
drain-source fissata, fluisce una corrente che poi decresce con l’aumentare
della tensione di gate (la polarità dipende dal fatto che il dispositivo sia di
tipo n o di tipo p). L’E-MOSFET non lascia passare alcuna corrente per
tensione di gate nulla e l’intensità della corrente drain-source aumenta al
crescere del modulo della tensione di gate al di sopra di un valore di soglia
(creazione dello strato di inversione, ossia del canale conduttivo fra source
e drain per induzione delle cariche).
Le caratteristiche di uscita IDS = f(VDS ) sono simili a quanto visto per il
JFET, infatti distingueremo ancora una regione omhica o lineare e una
regione di saturazione in cui la dipendenza della corrente dalla tensione
drain-source è poco accentuata. Un fenomeno caratteristico dei MOSFET è
la cosiddetta modulazione della lunghezza di canale che è simile a quanto
è noto nei BJT come effetto Early. Infatti, prolungando nel quadrante
adiacente tutte le caratteristiche d’uscita in zona di saturazione, queste si
incontrano in un punto a VDS = 1/λ , spesso anch’essa chiamata tensione di
Early. Valori tipici di λ variano tra 0.01 e 0.03 V-1.
In generale si evidenzia che per ottenere gli stessi valori di corrente e di
resistenza di canale che si ottengono in un transistore n-MOS, un
transistore p-MOS occupa un’area circa 3 volte maggiore. Quindi, a parità
di complessità, i circuiti integrati a n-MOS sono più piccoli di quelli a pMOS. Le minori dimensioni degli n-MOS, inoltre, rendono questi ultimi
più veloci poiché il contributo capacitivo è di entità inferiore e quindi nelle
applicazioni pratiche, si prilivegia l’uso di transistori MOSFET a canale n.
2.50e-4
V = 5V
GS
Drain-Source Current (A)
2.00e-4
1.50e-4
V = 4V
GS
1.00e-4
VGS= 3 V
5.00e-5
V = 2V
GS
0.00e+0
-5.00e-5
0
2
4
6
8
10
12
Drain-Source Voltage (V)
Output characteristics of an n-channel E-MOSFET that shows the effects of
channel length modulation adding a (1+VDS) dependence
Corrente IDS in zona di saturazione per un E-MOSFET a canale n:
(VDS >(VGS –VTN ) )
IDS = Kn /2(VGS –VTN )2
dove Kn è definito parametro di transconduttanza [A/V2] e VTN è la
tensione di soglia (>0 per un NMOS), dipendenti dalle caratteristiche
strutturali del dispositivo.
250
Drain-Source Current (uA)
En han cement-Mod e
200
Dep letion-Mod e
150
100
50
0
V = -2 V
V = +2 V
TN
TN
-50
-4
-2
0
2
4
Gate-Source Voltage (V)
Transfer characteristics for enhancement-mode
and depletion-mode NMOS transistors
6
Si noti che la corrente di saturazione di un JFET, già espressa come
IDS = IDSS (1 - VGS / VPO )2
può porsi in forma analoga a quella dell’E-MOSFET, e cioè:
IDS = Kn /2(VGS –VPO )2
con Kn = 2 IDSS /(VPO )2
IDSS = (VPO )2 Kn /2
ovvero
D
D
G
G
B
B
S
S
(a) NMOS enhancement-mode device
(b) PMOS enhancement-mode device
D
D
G
G
B
B
S
(c) NMOS depletion-mode device
S
(d) PMOS depletion-mode device
D
G
D
G
S
(e) Three-terminal NMOS transistor
S
(f) Three-terminal PMOS transistor
IEEE Standard MOS transistor circuit symbols
Polarizzazione di un E-MOSFET a canale n
I DS
70 k 
100 k 
RL
R2
D
VGG
G
10 V
S
30 k 
VDD
R1
10 V
V =1V
TN
Kn = 25 A/V 2
Constant gate voltage bias using a voltage divider
R
R
D
21 k 
EQ
100 k 
EQ
G
V
+
3V
I
+
L
VDS
S
-
I DS
VGS
G
-
Simplified MOSFET bias circuit
VDD
10 V
Equazioni alle maglie d’ingresso e di uscita:
VEQ = IG REQ + VGS
VDD = IDS RL + VDS
Essendo IG =0 risulta VEQ = VGS = 3 V
Per determinare la corrente di drain si può agire per via analitica,
ipotizzando il MOSFET in zona di saturazione e applicando quindi
l’espressione per il calcolo di IDS noti i valori di Kn e VTN , ovvero per via
grafica sul piano delle caratteristiche di uscita tracciando la retta di carico.
Attraverso la determinazione analitica si ottiene:
IDS = Kn /2(VGS –VTN )2 = 25/2*(3-1)2 = 50 A
e dalla seconda equazione si ricava VDS = VDD - IDS RL = 5 V
Il valore calcolato di VDS risulta maggiore di (VGS –VTN ) = 2 V quindi il
transistore si trova effettivamente in zona di saturazione come da ipotesi di
lavoro.
1.50e-4
1.25e-4
VGS= 4 V
Drain Current (A)
1.00e-4
7.50e-5
Q-Point
VGS= 3 V
5.00e-5
2.50e-5
VGS= 2 V
Lo ad Line
0.00e+0
-2.50e-5
0
2
4
6
8
10
Drain-Source Voltage (V)
Load line for the circuit under analysis
12
Il FET in regime dinamico
Analogamente a quanto visto per il BJT, il FET considerato come un
biporta può essere analizzato in regime dinamico partendo da un modello
generale a parametri y:
i1 = y11v1 + y12 v2
i2 = y21v1 + y22 v2
dove v1= vgs , i1 = ig, v2= vds , i2 = ids
e quindi:
ig = y11vgs + y12 vds
ids = y21vgs + y22 vds
Si ricorda che le variabili d’ingresso e di uscita sopra riportate
rappresentano la parte tempo-variante delle tensioni e delle correnti totali,
ossia piccole variazioni rispetto ai valori corrispondenti al punto di riposo.
Dal modello analitico si ricava che:
y11 = ig/vgs @ vds = 0
y12 = ig/vds @ vgs = 0
y21 = ids/vgs @ vds = 0
y22 = ids/vds @ vgs = 0
 Per le proprietà dei FET di avere assorbimento di corrente
trascurabile (JFET) o nullo (MOSFET) al terminale di gate, si
avrà y11 = 0
 Risulta inoltre anche nulla l’influenza dell’uscita sulla porta
d’ingresso, cioè y12 = 0
 y21 = gm è la transconduttanza
pari a ≈ √(2 Kn IDS ) per il MOSFET
e a 2 IDSS (VGS –VPO )/(VPO )2 per il JFET
 y22 = IDS /( VDS +1/ro con ro resistenza differenziale di uscita
L’espressione della transconduttanza evidenzia che nel BJT gm è
direttamente proporzionale ad IC mentre nel FET cresce con il fattore
√ IDS.
Inoltre, il fattore di amplificazione f già definito come f = gm ro , nei
BJT è praticamente indipendente dal punto di lavoro per VA» VCE poiché è
f = (VA+ VCE )/VT
Invece nei FET può essere espresso in maniera semplificata come:
f = 1/√ (2KN/ IDS )
e quindi risulta decrescere all’aumentare della corrente di polarizzazione.
A basse correnti, i valori di f , gm e ro sono abbastanza simili nei due tipi
di transistori, ma con l’aumento della corrente di drain nei FET gm non
aumenta altrettanto a quanto avviene del BJT con l’aumento della corrente
di collettore. Inoltre la ro diminuisce e quindi, a valori di IDS superiori a
10-5 A, si osserva una progressiva diminuzione di f .
Table 13.2 - BJT Small-Signal Parameters Versus Current
o = 100 VA = 75 V VCE = 10 V
IC
gm
r
ro
F
1 A
4 x 10-5 S
2.5 M
85 M
3400
10 A
4 x 10-4 S
250 k
8.5 M
3400
100 A
0.004 S
25 k
850 k
3400
1 mA
0.04 S
2.5 k
85 k
3400
10 mA
0.40 S
250 
8.5 k
3400
Table 13.3 - MOSFET Small-Signal Parameters Versus Current
Kn = 1 mA/V2  = .0133 V-1 VDS = 10 V
ID
gm
r
ro
F
1 A
4.76 x 10-5 S
?
85.2 M
4060
10 A
1.51 x 10-4 S
?
8.52 M
1280
100 A
4.76 x 10-4 S
?
852 k
406
1 mA
1.51 x 10-3 S
?
85.2 k
128
10 mA
4.76 x 10-3 S
?
8.52 k
40.0
Si noti che mentre nel BJT il regime di piccolo segnale è ammesso per
valori molto piccoli delle variazioni di Vbe (<5 mV) ed è indipendente
dalla corrente di polarizzazione, nei FET è molto più elevato e dipende
dalla corrente, potendo assumere valori anche superiori al volt. I FET
quindi presentano un range di linearità molto più ampio.
Modello a piccolo segnale per i FET
G
id
ig
+
+
v
gs
D
r
g v
m gs

-
v
ds
S
Small-signal model for the JFET, MOSFET
Amplificatore a JFET in configurazione a source comune.
+12 V
27 k 
R
D
C3
1k 
•
+
C1
•
v
R
RS
v
OUT
R
R
S
R
G
1 M
C2
2k
Common-source amplifier using a junction field-effect transistor.
For the JFET, IDSS = 1 mA, VP = -1 V,  = .02 V-1.
V
DD
= +12 V
27 k 
ID
IG
+
1M
-
3
100 k 
R4
IN
+
VDS
VGS
-
IS
2k
Circuit for determining the Q-point of the JFET
O
•
R
D
27 k 
+
1k 
vo
ROUT
RS
R
R
vs
R
G
3
100 k 
R4
IN
1 M
2k
Construction of the ac equivalent circuit
1k 
RD
R3
v
R
S
v
s
+
R
o
G
1 M
27 k 
Re-drawn version of the small-signal circuit
100 k 
-
999 
0.999 vs
+
+
ro
v
v
gs
-
g v
m gs
o
21.3 k 
-
Simplified ac equivalent circuit employing the JFET model
Applicando la trasformazione secondo Thevenin in ingresso si ha :
vTH = 0.999 vS , RTH = 999 
Valutiamo ora l’espressione dell’amplificazione di tensione in relazione a
vTH , cioè AVth = vo/ vTH .
Alla maglia di uscita si ha: vo = - gm vgs RL con RL = ro || RD || R3
A causa della resistenza d’ingresso infinita del JFET, la tensione vTH
coincide con la tensione vgs e quindi:
AVth = - gm RL
L’amplificazione complessiva AV = vo/ vs risulterà rispetto ad AVth
diminuita del rapporto di partizione RG / RG + RS , ma quando i valori
sono molto sbilanciati (come nel caso in esame, che spesso si verifica) si
ottiene AVth ≈ AV .
Determinazione della resistenza d’ingresso
R3
RD
RG
R IN
27 k 
1M
100 k 
(a)
R
G
+
v
R IN
g v
gs
1M
ro
m gs
21.3 k 
-
(b)
(a) Ac equivalent circuit for determining RIN
(b) Small-signal model for the circuit in (a)
Risulta evidente che RIN = RG e cioè che la resistenza d’ingresso
dell’amplificatore è legata unicamente alla resistenza di polarizzazione,
essendo infinita quella propria del FET.
Determinazione della resistenza di uscita
1k
1M
R
27 k 
R
D
AC equivalent circuit for determining ROUT
OUT
+
1k
1 M  vgs
R
g v
m gs
ro
Circuit with small signal model for the determination of ROUT
La resistenza di uscita è quindi data da: ROUT = ro || RD
D
27 k 
R OUT