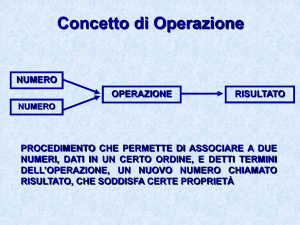
Operatori di confronto:
confrontano tra loro due numeri e come risultato danno come risposta vero o falso
operatore
si legge
esempio
risposta
=
uguale a
3=3
5=7
vero
falso
≠
diverso da
3≠3
5≠7
3>2
3>3
3>5
3<5
3<3
3<2
3≥2
3≥3
3≥5
3≤5
3≤3
3≤2
falso
vero
>
maggiore di
<
minore di
≥
maggiore o uguale a
≤
minore o uguale a
vero
falso
falso
vero
falso
falso
vero
vero
falso
vero
falso
falso
Esempi: 30 + 9 = 39 ; ݎ݁ݒ15 = 17 − 2 ; ݎ݁ݒ12 − 9 = 21 ݂݈ܽ; ݏ
25 > 39 ݂݈ܽ ; ݏ39 < 30 + 9 ݂݈ܽ ; ݏ42 ≥ 6 ∙ 7 ; ݎ݁ݒ40 ≤ 6 ∙ 7 ݎ݁ݒ
Parentesi
In matematica si usano le parentesi: ( ) per indicare che i calcoli che si trovano al loro
interno vanno eseguiti per primi.
Esistono tre tipi di perentesi:
tonde
(
)
quadre
[
]
graffe
{
}
prima si svolgono i calcoli racchiusi tra parentesi tonde, poi quelli racchiusi tra parentesi
quadre e quindi quelli racchiusi tra parentesi graffe. Ogni volta che si concludono i
calcoli all’interno di una coppia di parentesi si ottiene un singolo numero e le parentesi
possono essere cancellate. Con un esempio:
30 + ሾ2 + 7 + ሺ23 + 5ሻሿ + 9 = 30 + ሾ2 + 7 + 28ሿ + 9 = 30 + 37 + 9 = 76
Uso delle lettere in matematica
Spesso in matematica si usano le lettere. Questo non significa che l’italiano si mescola
con la matematica, assolutamente no! Si utilizzano le lettere perché sono simboli che
tutti noi conosciamo e non abbiamo difficoltà a riconoscere. In matematica hanno la
funzione di “contenitori” nei quali posso andare ad inserire dei numeri. Quali? Quelli che
voglio (sempre che non ci siano restrizioni… e in certi casi, come vedremo, sono
necessarie, cioè non proprio tutti i numeri potranno essere messi in questi contenitori).
Le lettere si usano quindi come segnaposto per dire “qui ci va un numero”, se una lettera
compare in più posti allora dovunque essa compare dovrò mettere lo stesso numero.
Facciamo un esempio: quando guardiamo il tachimetro dell’auto o dello scooter
leggiamo la velocità del mezzo. Essa è espressa in chilometri orari, ovvero il numero di
chilometri che posso percorrere se per un’ora mantengo la stessa velocità. Quindi la
velocità è il rapporto tra spazio percorso e tempo impiegato a percorrerlo cioè spazio
diviso tempo e si può esprimere anche in metri al secondo (quanti metri percorro in un
secondo). Se traduco in formula quanto detto scriverò: ݐ݈݅ܿ݁ݒà = ݅ݖܽݏ: ݉݁ݐ. Scritto
così è un po’ ingombrante allora si usano le lettere iniziali per rendere più compatta la
formula ݏ = ݒ: ݐ. Se ora voglio sapere a quale velocità mi sto muovendo, mi basta
misurare quanti metri percorro e quanti secondi ci metto a percorrerli, otterrò due
numeri (!) che dovrò andare a mettere nei “contenitori appositi” della formula e quindi
calcolare la velocità con una semplice divisione (usando la calcolatrice ;-).
Quindi in matematica quando usiamo le lettere in realtà stiamo usando dei simboli
“segnaposto” per dire: qui ci va un numero, appena decido (trovo, misuro,…) quale ce
lo metto. Poiché le lettere sono contenitori di numeri vedremo in seguito che anche su di
esse potrò applicare, con le dovute attenzioni, le operazioni aritmetiche e molto altro.
Addizione
L’addizione è una operazione che si svolge tra due numeri chiamati addendi e dà come
risultato un terzo numero chiamato somma
30 + 2 = 32
addizione
addendi
somma
Una sequenza di addizioni tra più numeri si svolge sempre da sinistra verso destra:
30 + 2 + 12 + 4 = 32 + 12 + 4 = 44 + 4 = 48
• Proprietà commutativa
30 + 2 = 2 + 30 = 32
Cambiando l’ordine degli addendi la somma non cambia, con una formula
ܽ+ܾ =ܾ+ܽ
• Proprietà associativa
30 + 2 + 12 = ሺ30 + 2ሻ + 12 = 30 + ሺ2 + 12ሻ = 44
La somma di tre (o più) addendi non cambia se al posto di coppie di essi si sostituisce la
loro somma. Con una formula
ܽ + ܾ + ܿ = ሺܽ + ܾሻ + ܿ = ܽ + ሺܾ + ܿሻ
Vediamo un esempio:
Eseguiamo da sinistra verso destra
Associamo i primi due addendi
Associamo gli ultimi due addendi
30 + 2 + 12
32 + 12
44
ሺ30 + 2ሻ + 12
32 + 12
44
30 + ሺ2 + 12ሻ
30 + 14
44
Abbiamo ottenuto lo stesso risultato!
Quando ci possono essere utili queste proprietà? Facciamo un esempio:
17 + 12 + 3 + 88 = 17 + 3 + 12 + 88 = ሺ17 + 3ሻ + ሺ12 + 88ሻ = 20 + 100 = 120
Ancora un trucco: noi sappiamo che
30 + 2 = 32 , vero!
L’operazione è reversibile? La risposta è sì, infatti
32 = 30 + 2 , vero!
(esistono infiniti modi di scrivere 32 e, più in generale, un qualsiasi numero)
Quando ci può essere utile questo trucco? Facciamo un esempio: calcoliamo la seguente
addizione senza usare la calcolatrice:
23 + 57 + 42 = ?
scriviamo 23 come 20 + 3 , 57 come 50 + 7 e 42 come 40 + 2 e otteniamo
20 + 3 + 50 + 7 + 40 + 2
applichiamo la proprietà commutativa (più volte) e otteniamo
20 + 50 + 40 + 3 + 7 + 2
e grazie alla proprietà associativa applicata più volte otteniamo
ሺ20 + 50ሻ + 40 + ሺ3 + 7ሻ + 2
70 + 40 + 10 + 2
ሺ70 + 40ሻ + ሺ10 + 2ሻ
110 + 12
122
Anche se non sembra abbiamo svolto in riga quello che si fa nelle adizioni in colonna!
Scrivere un numero come addizione tra altri due è sempre possibile, ad esempio:
numero
5
9
12
37
…scritto come addizione
4 + 1 ;3 + 2 ; 2 + 3 ;1 + 4
8 + 1 ;7 + 2 ; 6 + 3 ;5 + 4 ;4 + 5 ;3 + 6 ;2 + 7 ; 1 + 8
11 + 1 ; 10 + 2 ; 9 + 3 ; 8 + 4 ; 7 + 5 ; 6 + 6; …
30 + 7 ; 17 + 20 ; 29 + 8 ; 33 + 4 ; 23 + 14 ; 3 + 36; …
Possiamo quindi affermare che la somma di due o più addendi non cambia se ad uno o a
più di uno di essi se ne sostituiscono altri la cui somma è uguale all'addendo sostituito
Moltiplicazione
La moltiplicazione è un modo sintetico di indicare una addizione ripetuta. Infatti se
scriviamo:
5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 = 45
È chiaro che occupa parecchio spazio, allora per risparmiare in scrittura osservo che il 5
compare 9 volte nella addizione ripetuta, introduco allora una scrittura (operazione) più
compatta per esprimere ciò ovvero
5 ∙ 9 = 45
Numero che deve essere
addizionato a se stesso
Numero di volte in cui 5 compare nella
addizione ripetuta
Simbolo che esprime la
nuova operazione
La moltiplicazione quindi è una operazione che si svolge tra due numeri chiamati fattori
e dà come risultato un terzo numero chiamato prodotto
30 ∙ 2 = 60
moltiplicazione
fattori
prodotto
Una sequenza di moltiplicazioni tra più numeri si svolge sempre da sinistra verso destra:
30 ∙ 2 ∙ 12 ∙ 4 = 60 ∙ 12 ∙ 4 = 720 ∙ 4 = 2880
• Proprietà commutativa
30 ∙ 2 = 2 ∙ 30 = 60
Cambiando l’ordine dei fattori il prodotto non cambia, con una formula
ܽ∙ܾ =ܾ∙ܽ
• Proprietà associativa
30 ∙ 2 ∙ 12 = ሺ30 ∙ 2ሻ ∙ 12 = 30 ∙ ሺ2 ∙ 12ሻ = 720
Il prodotto di tre (o più) fattori non cambia se al posto di coppie di essi si sostituisce il
loro prodotto. Con una formula
ܽ ∙ ܾ ∙ ܿ = ሺܽ ∙ ܾሻ ∙ ܿ = ܽ ∙ ሺܾ ∙ ܿሻ
Vediamo un esempio:
Eseguiamo da sinistra verso destra
Associamo i primi due fattori
Associamo gli ultimi due fattori
30 ∙ 2 ∙ 12
60 ∙ 12
720
ሺ30 ∙ 2ሻ ∙ 12
60 ∙ 12
720
30 ∙ ሺ2 ∙ 12ሻ
30 ∙ 24
720
Abbiamo ottenuto lo stesso risultato!
Quando ci possono essere utili queste proprietà? Facciamo un esempio:
4 ∙ 3 ∙ 5 = 3 ∙ 4 ∙ 5 = 3 ∙ ሺ4 ∙ 5ሻ = 3 ∙ 20 = 60
Ancora un trucco: noi sappiamo che
30 ∙ 2 = 60 , vero!
L’operazione è reversibile? La risposta è sì, infatti
60 = 30 ∙ 2 , vero!
Quando ci può essere utile questo trucco? Facciamo un esempio: calcoliamo la seguente
moltiplicazione senza usare la calcolatrice:
45 ∙ 140 = ?
scriviamo 140 come 10 14 otteniamo
45 · 10 · 14
applichiamo la proprietà associativa e otteniamo
ሺ45 · 10ሻ · 14
450 · 14
scriviamo 14 come 2 7 e otteniamo
450 · 2 · 7
900 · 7
scriviamo 900 come 100 9 e otteniamo
100 · 9 · 7
applichiamo la proprietà associativa e otteniamo
100 · ሺ9 · 7ሻ
100 · 63
6300
Scrivere un numero come moltiplicazione tra altri due è sempre possibile (anche se il
numero è primo), ad esempio:
numero
5
21
45
72
…scritto come moltiplicazione
5 ∙ 1 ;1 ∙ 5
7 ∙ 3 ; 3 ∙ 7 ; 21 ∙ 1 ; 1 ∙ 21
5 ∙ 9 ; 9 ∙ 5 ; 15 ∙ 3 ; 3 ∙ 15 ; 45 ∙ 1 ; 1 ∙ 45
8 ∙ 9 ; 36 ∙ 2 ; 24 ∙ 3 ; 18 ∙ 4 ; 12 ∙ 6 ; 9 ∙ 8 ; 6 ∙ 12 ; …
Possiamo quindi affermare che il prodotto di due o più fattori non cambia se ad uno o a
più di uno di essi se ne sostituiscono altri il cui prodotto è uguale al fattore sostituito
• Proprietà distributiva della moltiplicazione rispetto all’addizione
È sicuramente la proprietà “più importante” dell’aritmetica e ci permette di distribuire la
moltiplicazione sugli addendi di una addizione, vediamo come:
5 ∙ ሺ7 + 4ሻ = 5 ∙ 7 + 5 ∙ 4
La proprietà è reversibile? La risposta è sì, infatti
5 ∙ 7 + 5 ∙ 4 = 5 ∙ ሺ7 + 4ሻ
E non solo
ሺ7 + 4ሻ ∙ 5 = 5 ∙ ሺ7 + 4ሻ = 5 ∙ 7 + 5 ∙ 4 = 7 ∙ 5 + 4 ∙ 5
applico la proprietà commutativa
Che equivale a scrivere
ሺ7 + 4ሻ ∙ 5 = 7 ∙ 5 + 4 ∙ 5
Quando ci può essere utile questa proprietà? Facciamo un esempio: calcoliamo la
seguente moltiplicazione senza usare la calcolatrice:
23 ∙ 14 = ሺ20 + 3ሻ ∙ ሺ10 + 4ሻ = ሺ20 + 3ሻ ∙ 10 + ሺ20 + 3ሻ ∙ 4 =
20 ∙ 10 + 3 ∙ 10 + 20 ∙ 4 + 3 ∙ 4 = 200 + 30 + 80 + 12 = 322
Anche se non sembra abbiamo svolto in riga quello che si fa nelle moltiplicazioni in colonna!
Infatti è grazie a questa proprietà che “funziona” l’algoritmo della moltiplicazione in colonna.
Con una formula
ܽ ∙ ሺܾ + ܿሻ = ܽ ∙ ܾ + ܽ ∙ ܿ
Che come abbiamo visto è reversibile, cioè
ܽ ∙ ܾ + ܽ ∙ ܿ = ܽ ∙ ሺܾ + ܿሻ
Inoltre, poiché vale la proprietà commutativa per la moltiplicazione, la proprietà
distributiva vale anche a destra, cioè
ሺܾ + ܿሻ ∙ ܽ = ܽ ∙ ሺܾ + ܿሻ = ܽ ∙ ܾ + ܽ ∙ ܿ = ܾ ∙ ܽ + ܿ ∙ ܽ
Con un altro esempio
ሺ2 + 5ሻ ∙ 3 = 3 ∙ ሺ2 + 5ሻ = 3 ∙ 2 + 3 ∙ 5 = 2 ∙ 3 + 5 ∙ 3
Come abbiamo detto la moltiplicazione equivale ad una addizione ripetuta nella quale
uno dei due fattori compare un numero di volte pari all’altro fattore, valendo la proprietà
commutativa possiamo scrivere:
12 compare 6 volte
12 ∙ 6 = 12 + 12 + 12 + 12 + 12 + 12 = 72
oppure
6 compare 12 volte
12 ∙ 6 = 6 + 6 + 6 + 6 + 6 + 6 + 6 + 6 + 6 + 6 + 6 + 6 = 72
Sottrazione
La sottrazione è una operazione che si svolge tra due numeri chiamati rispettivamente
minuendo e sottraendo e dà come risultato un terzo numero chiamato differenza
30 − 6 = 24
minuendo
sottrazione
sottraendo
differenza
Una sequenza di sottrazioni tra più numeri si svolge sempre da sinistra verso destra:
30 − 2 − 12 − 4 = 28 − 12 − 4 = 16 − 4 = 12
• Proprietà invariantiva
36 − 12 = ሺ36 + 7ሻ − ሺ12 + 7ሻ = 43 − 19
36 − 12 = ሺ36 − 4ሻ − ሺ12 − 4ሻ = 32 − 8
La differenza di una sottrazione non cambia se sottraggo o aggiungo sia al minuendo che
al sottraendo uno stesso numero purché minore o uguale al sottraendo, con una formula
ܽ − ܾ = ሺܽ ± ܿሻ − ሺܾ ± ܿሻ
ܿ≤ܾ
La moltiplicazione è distributiva anche rispetto alla sottrazione, vale quindi quanto visto
per proprietà distributiva rispetto all’addizione, cioè
ܽ ∙ ሺܾ − ܿሻ = ܽ ∙ ܾ − ܽ ∙ ܿ
Divisione esatta
La divisione esatta è una operazione che si svolge tra due numeri chiamati
rispettivamente dividendo e divisore che dà come risultato un terzo numero chiamato
quoziente. Con la divisione esatta si ricerca quel numero (quoziente) che moltiplicato per
il divisore da come prodotto il dividendo
30 ∶ 2 = 15
dividendo
divisione
quoziente
divisore
Una divisione intera può essere interpretata anche come una sottrazione ripetuta dove al
dividendo sottraggo il divisore il numero di volte necessario ad ottenere zero (tale
numero volte sarà pari al quoziente). Ad esempio:
30 ∶ 5 = 6 ovvero 30 − 5 − 5 − 5 − 5 − 5 − 5 = 0
6 volte (quoziente = 6)
Una sequenza di divisioni tra più numeri si svolge sempre da sinistra verso destra:
60 ∶ 2 ∶ 5 ∶ 3 = 30 ∶ 5 ∶ 3 = 6 ∶ 3 = 2
• Proprietà invariantiva
36 ∶ 12 = ሺ36 ∶ 3ሻ ∶ ሺ12 ∶ 3ሻ = 12 ∶ 4
Il quoziente di una divisione non cambia se moltiplico o divido sia il dividendo che il
divisore per uno stesso numero diverso da zero purché la divisione sia possibile
nell’insieme dei numeri Naturali, in formule
ܽ ∶ ܾ = ሺܽ ∙ ܿሻ ∶ ሺܾ ∙ ܿሻ
ܽ ∶ ܾ = ሺܽ ∶ ܿሻ ∶ ሺܾ ∶ ܿሻ
ܿ divide ܽ e ܾ
• Proprietà distributiva a destra
ሺ24 + 12ሻ ∶ 4 = ሺ24 ∶ 4ሻ + ሺ12 ∶ 4ሻ = 6 + 3
ሺ24 − 12ሻ ∶ 4 = ሺ24 ∶ 4ሻ − ሺ12 ∶ 4ሻ = 6 − 3
Con una formula
ሺܽ ± ܾሻ ∶ ܿ = ܽ ∶ ܿ ± ܾ ∶ ܿ
Che, come visto per la moltiplicazione, è reversibile, cioè
ܽ ∶ ܿ ± ܾ ∶ ܿ = ሺܽ ± ܾሻ ∶ ܿ
La divisone non è distributiva a sinistra, cioè
ܽ ∶ ሺܾ ± ܿሻ ∶ ܿ ≠ ܽ ∶ ܾ ± ܽ ∶ ܿ
• Divisione con la tavola Pitagorica
Se il dividendo è un numero a due cifre e il divisore un numero ad una cifra posso
consultare la tavola pitagorica in corrispondenza della tabellina del divisore, indice di
colonna, e cercare il dividendo.
o Se lo trovo leggo sulla stessa riga, a sinistra tra gli indici di riga, il quoziente.
Esempio: calcoliamo 72 ∶ 8
Cerco 72 nella tabellina dell’8
Indici di colonna
sulla stessa riga, a sinistra, leggo il quoziente
Indici di riga
In queste tavole mancano la tabellina dell’1 e del 10 perché dividere per essi è molto semplice
o Può però accadere che il dividendo non sia presente nella tabellina del
divisore come, ad esempio, nell’eseguire questa divisione 72 ∶ 3
Se osservo la tabellina del 3 non troverò 72, come fare?
Guardo dove si trova 72 nella tavola Pitagorica e noto che è presente
nella tabellina dell’8 e del 9 ( 9 ∙ 8 = 72 ), tra i fattori che lo compongono
cerco quello che compare nella tabellina del 3, cioè 9 ( 9 = 3 ∙ 3 ); allora
per la proprietà associativa della moltiplicazione
posso scrivere che
72 = 9 ∙ 8 = ሺ3 ∙ 3ሻ ∙ 8 = 3 ∙ ሺ3 ∙ 8ሻ = 3 ∙ 24
E quindi 72 ∶ 3 = 24
Facciamo un altro esempio: 56 ∶ 4 , anche in questo caso 56 non
compare nella tabellina del 4 ma in quella del 7 e dell’8 ( 7 ∙ 8 = 56 ), tra i
fattori che lo compongono cerco quello che compare nella tabellina del
4, cioè 8 ( 8 = 4 ∙ 2 ); allora posso scrivere che
56 = 7 ∙ 8 = 7 ∙ ሺ4 ∙ 2ሻ = 7 ∙ ሺ2 ∙ 4ሻ = ሺ7 ∙ 2ሻ ∙ 4 = 14 ∙ 4
E quindi 56 ∶ 4 = 14
o Se quanto detto non è applicabile dovrò utilizzare uno dei metodi che
seguono.
Divisione con resto
Nella divisione con dividendo un numero a due cifre e divisore un numero ad una
cifra, se non è possibile trovare un numero che moltiplicato per il divisore dia come
risultato il dividendo o il divisore è minore del prodotto del divisore per 10 posso
procedere in questo modo:
o si cerca il più grande multiplo1 del divisore minore del dividendo
o leggo sulla stessa riga, a sinistra tra gli indici di riga, il quoziente
o si sottrae al dividendo il numero trovato, la differenza darà il resto
Esempio: calcoliamo 40 ∶ 6
Nella tabellina del 6 trovo 36<40
sulla stessa riga, a sinistra, leggo il quoziente
Eseguo la sottrazione: 40 − 36 = 4
Quindi 40 ∶ 6 = 6 con resto 4
o Può però accadere che il multiplo cercato non sia presente nella tabellina
del divisore come, ad esempio, nell’eseguire questa divisione 65 ∶ 3
Se osservo la tabellina del 3 non troverò numeri maggiori di 30, come
fare?
Cerco nelle tabelline dei multipli di 3 ( 6 e 9 ) il più grande dei loro
multipli minori di 65, nel nostro caso 63 che trovo nella tabellina del 9,
tra i fattori che lo compongono cerco quello che compare nella tabellina
del 3 ( 9 = 3 ∙ 3 ) allora posso scrivere che
63 = 9 ∙ 7 = ሺ3 ∙ 3ሻ ∙ 7 = 3 ∙ ሺ3 ∙ 7ሻ = 3 ∙ 21
e 65 − 63 = 2
e quindi si ricava 63 ∶ 3 = 21 con resto 2
Algoritmo della divisione (caso generale)
1
I multipli di un numero sono tutti i numeri che si ottengono moltiplicando quel numero per tutti gli altri numeri
naturali (in generale per tutti gli altri interi); i sottomultipli di un numero sono tutti i numeri naturali (in generale
interi) che dividono quel numero senza resto.
Esiste un algoritmo2 (lo hai imparato alle elementari) che funziona sempre ed è
basato sulla applicazione, anche ripetuta più volte, dei due metodi precedenti,
vediamo come: calcoliamo 83 ∶ 6
Chiaramente il dividendo è maggiore di 10 volte il divisore, infatti 83 > 60
(se fosse uguale il risultato della divisione sarebbe ovvio, se fosse minore userei i metodi precedenti)
Disegniamo il seguente schema e ci disponiamo i numeri
dividendo
83
6
divisore
schema della divisione
spazio per i resti parziali e resto finale
spazio per il quoziente
Comincio con la cifra più a sinistra del divisore e controllo se è divisibile per il
divisore, in questo caso lo è ma con resto ( 8 ∶ 6 = 1 con resto 2 ). Scriverò quindi:
resto parziale
83 6
2
1
quoziente parziale
Il resto ottenuto in realtà non ha valore di 2 unità ma di 2 decine (20 unità) a cui
aggiungere le 3 unità avanzate, scriverò quindi:
83 6
23 1
Mi chiedo quindi se nuovo numero ricavato (23) sia divisibile per 6, lo è ma con resto
( 23 ∶ 6 = 3 con resto 5 ). Scriverò quindi:
resto finale
83 6
2 3 13
5
Poiché 5 non è divisibile per 6 (è un resto!) ho terminato,
e quindi si ricava che 83 ∶ 6 = 13 con resto 5
in altre parole 83 = 13 ∙ 6 + 5
facciamo un altro esempio: calcoliamo 389 ∶ 7
389
2
7
Sequenza di passi elementari, anche ripetuti più volte, che permette di risolve un problema
La cifra più a sinistra del divisore non è divisibile per il divisore, quindi considero le
prime due (37) e verifico se formano un numero divisibile per il divisore, lo è ma con
resto ( 38 ∶ 7 = 5 con resto 3 ):
389 7
3
5
resto parziale
quoziente parziale
Il resto ottenuto in realtà non ha valore di 3 unità ma di 3 decine (30 unità) a cui
aggiungere le 9 unità avanzate, scriverò quindi:
389 7
39 5
Mi chiedo quindi se nuovo numero ricavato (39) sia divisibile per 7, lo è ma con resto
( 39 ∶ 7 = 5 con resto 4 ), scriverò quindi:
389 7
39 55
4
quoziente parziale
Poiché 4 non è divisibile per 7 (è un resto!) ho terminato,
e quindi si ricava che 389 ∶ 7 = 55 con resto 4
in altre parole 389 = 55 ∙ 7 + 4
• Proprietà invariantiva
36 ∶ 12 = ሺ36 ∶ 4ሻ ∶ ሺ12 ∶ 4ሻ = 9 ∶ 3
8 ∶ 2 = ሺ8 ∙ 5ሻ ∶ ሺ2 ∙ 5ሻ = 40 ∶ 10
Il quoziente di una divisione non cambia se divido o moltiplico sia dividendo che
divisore per uno stesso numero (purché non sia zero e nel caso della divisione sia
divisore esatto di entrambe), in formule
ܽ ∶ ܾ = ሺܽ ∶ ܿሻ ∶ ሺܾ ∶ ܿሻ
ܿ ≠ 0; ܿ divisore esatto di ܽ e ܾ
ܽ ∶ ܾ = ሺܽ ∙ ܿሻ ∶ ሺܾ ∙ ܿሻ
ܿ≠0
Potenze
Le potenze sono un metodo sintetico per esprimere la moltiplicazione di un numero per se stesso più volte
Significato di potenza: l’esponente indica quante volte compare la base in una sequenza di moltiplicazioni
Perché a^0 fa 1? Perché se divido a^n per a^n ottengo 1 e poiché la proprietà delle potenze dice che
a^n:a^m=a^n-m si ha che a^n:a^n=a^n-n=a^0 ed è anche vero che a^n:a^n=1 quindi a^0=1
A 0^0 non si da significato perché se dessimo valore 1 significherebbe che 0^n:0^n=0^n-n=0^0=1 contro la
regola che non si può dividere per zero
Operazioni con i numeri interi
Z
3 + 4 = ሺ+3ሻ + ሺ+4ሻ = +7 = 7
3 − 4 = ሺ+3ሻ − ሺ+4ሻ leggo la sottrazione da destra a sinistra (faccio ሺ+4ሻ − ሺ+3ሻ), ottengo 1 e gli cambio
segno
−3 + 4 = ሺ−3ሻ + ሺ+4ሻ = ሺ+4ሻ + ሺ−3ሻ = 4 − 3 = 1
−3 − 4 = ሺ−3ሻ − ሺ+4ሻ = ሺ−3ሻ + ሺ−4ሻ = −7