MISURE MECCANICHE E TERMICHE
A.A. 2012-2013
Lezione n.22 (05.12.2012)
MISURE DI TEMPERATURA
STRUMENTI ELETTRICI
Possono essere di tipo attivo (termometri a termocoppia) o di tipo passivo (termometri a resistenza)
TERMOMETRI A TERMOCOPPIA
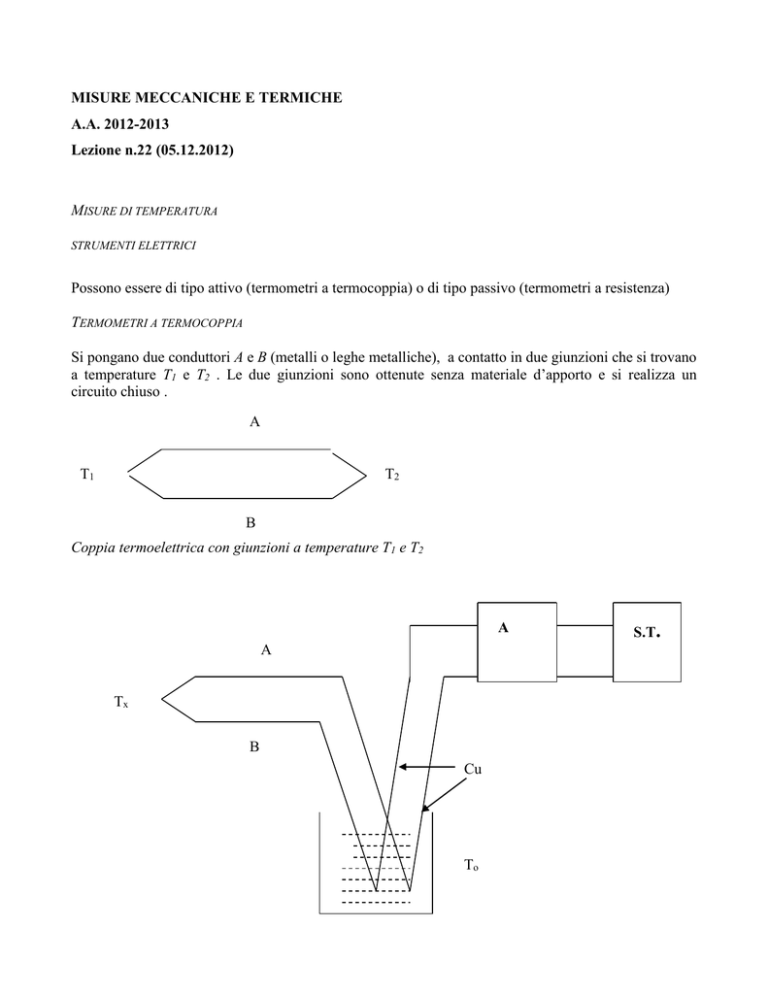
Si pongano due conduttori A e B (metalli o leghe metalliche), a contatto in due giunzioni che si trovano
a temperature T1 e T2 . Le due giunzioni sono ottenute senza materiale d’apporto e si realizza un
circuito chiuso .
A
T1
T2
B
Coppia termoelettrica con giunzioni a temperature T1 e T2
A
A
AA
Tx
B
Cu
To
S.T.
.
a)- se T1 e T2 sono uguali, si hanno alle giunzioni due barriere di potenziali (effetto Volta) uguali e
opposte, e nel circuito non circola corrente;
b)- se T1 e T2 sono diverse, le barriere di potenziale sono diverse (effetto Peltier), e nel circuito circola
corrente;
c)- in corrispondenza a gradienti di temperatura nei conduttori si hanno gradienti di potenziale (effetto
Thomson); questo terzo effetto è trascurabile rispetto ai primi due.
Termometro a termocoppia e catena di misura
Interrompendo il circuito si misura una f.e.m.(effetto termoelettrico); la f.e.m è funzione della natura
dei conduttori A e B e delle due temperature T1 e T2.
Per realizzare un sensore di temperatura, stabilita la coppia termoelettrica A B, si mantenga costante
una delle due temperature (T2 = To = cost.), e si faccia variare l’altra temperatura (T1 = Tx). La
giunzione a temperatura To viene detta giunto freddo, quella a temperatura Tx viene detta giunto caldo.
In queste condizioni la f.e. m. è funzione solo di Tx (temperatura variabile).
Nulla vieta di interrompere il circuito in corrispondenza a To e pertanto, supponendo di amplificare la
f.e.m. e di rilevare la tensione amplificata mediante un voltmetro (statico o dinamico, a seconda del
caso), si ha a che fare con una catena di misura come quella rappresentata in figura. Si osservi che, a
partire dal giunto freddo si adottano conduttori in materiale (per es., rame) diverso da A e B.
V
T
L’andamento della f.e.m. in funzione di Tx è parabolico: per Tx > To la f.e.m. è positiva, per Tx = To
la f.e.m. è nulla, per Tx < To . la f.e.m. è negativa; è possibile linearizzare la curva di graduazione in
intervalli di temperatura diversi.
La temperatura To si assume convenzionalmente pari a 0° C; ciò significa che il giunto freddo va
realizzato utilizzando il punto di fusione dell’acqua.
Le coppie termoelettriche standard, cioè quelle per le quali sono note, sotto forma di tabelle le V(T)
con To = 0°, sono in numero limitato, 7 fino a pochi anni fa, 8 oggi:
1)- Chromel (Ni –Cr) - Alumel (Ni-Al) : campo : -200°C – 1200 °C; sensibilità: circa 40 V/°C,
2)- Ferro – Costantana Cu-Ni) : campo : -40°C – 750 °C; sensibilità: circa 60 V/°C,
3)- Rame - Costantana, : campo : -200°C – 400 °C; sensibilità: circa 50 V/°C,
4)-Chromel - Costantana, : utilizzate a basse temperature; sensibilità: circa 70 V/°C
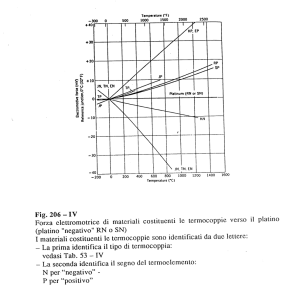
5) -Platino - Platino/Rodio con Rh al 10% : utilizzate per temperature fino a 1600 °C
6) -Platino - Platino/Rodio con Rh al 13% : utilizzate per temperature fino a 1600 °C
7) -Platino - Platino/Rodio con Rh al 30% : utilizzate per temperature fino a 1800 °C
8) – Nicrosil (Ni-Cr—Si) – Nisil (Ni –Si) : utilizzate fra 600°c e 1200 °c
La bassa sensibilità, dell’ordine delle decine di V/°C, ciò spiega perché nella catena di misura è
presente un amplificatore.
Nel caso non sia possibile realizzare il giunto freddo a 0° mediante ghiaccio fondente, si fa riferimento
a una To ≠ 0°C, si misura la V(Tx,To) cui si somma la V(To, 0°).
In alternativa, si può utilizzare un giunto di compensazione:
Questo può essere realizzato via hardware: con un termometro a resistenza si misura appunto la
temperatura T0 del giunto freddo; questa temperatura viene convertita nella tensione V(To, 0°) che
dipende dalla coppia termoelettrica; un circuito sommatore effettua l’operazione:
V(Tx, 0°) = V(Tx,To) + V(To, 0°).
In alternative si può operare via software inviando la V(To, 0°) a un PC che ha preventivamente
memorizzato la risposta della coppia termoelettrica ed effettua quindi le operazioni necessarie.
TERMOMETRI A RESISTENZA
I termometri a resistenza utilizzano come elemento sensibile un conduttore o un semiconduttore.
Nei primi, nei quali l’elemento sensibile è un conduttore, a una variazione di temperatura T
corrisponde una variazione di resistenza:
R = RoT,
ove Ro è la resistenza alla temperatura di riferimento To (0° C), e è il coefficiente di temperatura
della resistenza.
In linea di principio qualunque conduttore potrebbe essere utilizzato per realizzare un termometro a
resistenza. In pratica si escludono anzitutto le leghe perché basterebbe una piccola variazione di uno
degli elementi di lega per variare la risposta del termometro. Al metallo utilizzato si richiede un
coefficiente elevato per avere elevata sensibilità e quanto più possibile costante per avere una curva
di graduazione lineare; il metallo che meglio risponde a questa esigenza è il Platino (il Nichel ha un
coefficiente più elevato, ma il coefficiente di temperatura del Platino si mantiene pressoché costante
in un campo di temperature più ampio), e i termometri a resistenza utilizzati sono termometri a
resistenza di platino (TRP).
A 0° C la resistenza ha un valore standard pari a 100 ; nel campo 0 – 100 ° C il coefficiente può
ritenersi costante e pari a 0,00385 °C-1.
A seconda del campo di variazione della temperatura, e quindi di variazione della resistenza, la
variazione R si rileva mediante circuito a ponte (piccole variazioni di temperatura) o mediante circuito
voltamperometrico (variazioni di temperatura elevate).
Un TRP è costituito da un filamento di Platino avvolto su un supporto e opportunamente protetto. Il
filamento e il relativo supporto possono anche essere annegati in una matrice ceramica. La possibilità
di dover ricorrere a un circuito voltamperometrico impone un collegamento a 4 fili, due per
l’alimentazione in corrente, due per il rilievo della tensione.
La precisione dei TRP è molto elevata, tanto è vero che i TRP si assumono come termometri campione
per interpolare le temperature fra i punti fissi della ITS-90
Supporto
Filamento di platino
Guaina protettiva
Schema di TRP
Nel caso di misure a distanza, occorre , se si utilizza un ponte di Wheatstone, evitare errori dovuti alla
temperatura dei cavi di collegamento; per questa ragione si realizzano collegamenti a quattro fili, o, più
semplicemente, a tre fili; nel caso a quattro fili un cavo bipolare è collegato al TRP, l’altro ,sentendo la
stessa temperatura, trovandosi sul ramo contiguo del ponte, ne compensa gli effetti.
TRP
TRP con collegamento a quattro fili
TRP
TRP con collegamento a tre fili
Confrontando i TRP e le termocoppie, si può osservare che i TRP risultano più ingombranti e quindi
meno rapidi. Di contro, all’elevata precisione uniscono anche un’elevata sensibilità.
Nei termometri, nei quali l’elemento sensibile è un semiconduttore (termistori), si ha una diminuzione
della resistenza R all’aumentare della temperatura T; Se Ro è la resistenza alla temperatura di
riferimento To, risulta:
RT=Roe(1/T-1/To);
la sensibilità è elevata alle basse temperature; la precisione è modesta. Pertanto questi dispositivi
vengono usati come “indicatori”, più che come veri e propri termometri.
TERMOMETRI A RADIAZIONE
Tutti i corpi emettono radiazioni elettromagnetiche per il solo fatto di trovarsi a una temperatura
termodinamica superiore a zero. Si parla di radiazione termica, in quanto dovuta all’agitazione termica
di atomi e molecole, con riferimento particolare alla banda di lunghezze d’onda fra 0,3 e 1000 m; in
questa banda si trovano il visibile (0,38 – 0,76 m) e l’infrarosso (0,76 – 1000 m). Osservando un
corpo incandescente si osserva qualitativamente che la luce emessa varia di intensità e colore al variare
della temperatura.
Su queste osservazioni sono basate le leggi della radiazione termica.
Legge di Stefan-Boltzman (radiazione totale)
La potenza L emessa dal corpo nero per unità di superficie e di angolo solido in direzione normale alla
superficie emittente varia con la quarta potenza della temperatura termodinamica ed è data da:
L = T4/ (unità di misura nel SI: W m-2sr-1).
con = 5.6710-8 Wm-2K-4 .
Legge di Wien – Planck (radiazione specifica)
La potenza L emessa dal corpo nero per unità di superficie, di angolo solido e di intervallo di
lunghezza d’onda in direzione normale alla superficie emittente varia al variare della temperatura e
della lunghezza d’ondaed è data da:
c
1
L 15 c / T
(unità di misura nel SI: W m-3sr-1).
2
e
1
con c1 = 1,19110-16 Wm2 ; c2 = 1,4410-2 mK.
In figura sono riportate alcune L al variare della temperatura termodinamica T.
Temperature : 1600 K(rosso); 1800 K (blu); 2000 K (verde) , 2400 K (celeste).
Si può osservare che il massimo di L si sposta verso più basse all’aumentare della temperatura; vale
infatti la:
max T = 2898 mK.
Le relazioni relative alla radiazione totale e specifica valgono nel caso di potenza emessa in direzione
normale alla superficie emittente; nel caso, peraltro poco frequente nelle misure di temperatura, che ciò
non avvenga, vale la legge di Lambert (legge del coseno). Inoltre, le relazioni sono riferite al corpo
nero; per corpi reali occorre tener conto dell’emissività (totale , o spettrale , a seconda che ci si
riferisca alla radiazione totale o specifica). Valgono quindi le:
L re = L
L,re = L
Le emissività (totale e specifica) dipendono dalla temperatura.
A seconda che si faccia riferimento alla legge di Wien-Planck o a quella di Stefan-Boltzman si
realizzano particolari termometri o pirometri, che possono pertanto rilevare la potenza radiante
specifica o quella totale.
PIROMETRI MONOCROMATICI
Questi pirometri sono basati sul confronto fra l’intensità luminosa di una sorgente a temperatura
incognita e di quella di una sorgente a temperatura nota: se le due temperature sono identiche le
intensità luminose, ovvero le potenze specifiche emesse sono eguali.
Il confronto può essere affidato all’occhio dell’osservatore, come nel pirometro a filamento
scomparente .
Se la temperatura della lampada è superiore a quella della sorgente il filamento appare in rilievo e
viceversa; solo quando le due temperature sono eguali non si distingue il filamento dalla sorgente; per
la misurazione si varia la tensione di alimentazione della lampada finché tale condizione non si
verifica; il voltmetro è preventivamente tarato in unità di temperatura. Si utilizza un filtro rosso per
poter operare a temperature più basse, anche se non si scende generalmente sotto gli 800 °C.
Più modernamente, il confronto è affidato a un rivelatore costituito da una cella fotoelettrica (pirometro
fotoelettrico); il principio è lo stesso del pirometro precedente: la radiazione della sorgente e quella
della lampada vengono inviate alternativamente alla cella tramite un disco rotante provvisto di finestre
e un servosistema regola l’alimentazione della lampada finché le intensità luminose non coincidono; la
precisione è maggiore che nel caso precedente, e con celle fotoelettriche sensibili alle radiazioni
infrarosse non è necessario operare nel campo del visibile e si può quindi operare a temperature più
basse.
PIROMETRI A RADIAZIONE TOTALE
Quando si vogliano rilevare temperature relativamente basse, anche temperature dell’ordine della
temperatura ambiente, è conveniente far riferimento non a una (o due) lunghezze d’onda , ma a tutta la
banda di lunghezze d’onda in cui si hanno valori apprezzabili della radiazione.
Il principio di funzionamento di un pirometro a radiazione totale è quello di convogliare su un sensore
di radiazione, tramite un sistema di lenti o specchi, la potenza radiante proveniente da una sorgente di
radiazione.
In figura è mostrato un pirometro a radiazione totale in cui la radiazione proveniente dalla sorgente
entra dalla “finestra” A, è riflessa dallo specchio sferico B sul fuoco del diaframma J al centro del quale
si trova un’apertura C; la radiazione che passa attraverso C è riflessa dallo specchio sferico D sul
sensore di radiazione E; l’immagine della sorgente viene osservata dalla lente H posta dietro B.
Si faccia ora riferimento alla figura seguente in cui è rappresentata la sorgente emittente, e sia L la
potenza unitaria che in condizioni ideali perviene allo strumento; il pirometro è schematizzato con una
lente di diametro D e un sensore di radiazione di dimensione d; si faccia l’ipotesi che il sensore si trovi
nel fuoco della lente quando la sorgente si trova all’infinito (f : distanza lente-sensore); in tal caso la
potenza termica che può giungere al sensore è data da:
P = L ∙ D2/4∙ d 2/f 2
sorgente
L
D
P
d
f
In realtà, a causa dell’attraversamento del mezzo (atmosfera) che si trova tra sorgente e pirometro , la
radiazione subisce un’attenuazione; occorre pertanto tener conto della trasmissibilità A dell’atmosfera
che dipende fortemente dal contenuto di vapor d’acqua. Altro elemento di cui occorre tener conto è
quello costituito dalla potenza (unitaria) emessa dallo sfondo.
In definitiva:
P = (L sorg – L sfondo) ∙ A ∙ D2/4 ∙ d 2/f 2.
Il valore di P deve essere naturalmente superiore al valore dato dal rumore.
Si è fatto fin qui riferimento alla potenza che può giungere al sensore di radiazione; la temperatura del
sensore deve essere quanto più bassa possibile per limitare il rumore. Ma la temperatura del sensore
deve essere limitata per un’altra ragione: la sorgente si trova a una temperatura Tsorg , mentre il sensore
si trova a una temperatura Tsens; lo scambio termico è regolato dalla differenza delle quarte potenze
della temperatura,; in altre parole, con riferimento alla potenza unitaria e a corpi neri, lo scambio
termico è regolato dalla ∙(T4sorg – T4 sens).
Nel caso si debbano misurare temperature dell’ordine della temperatura ambiente, occorre effettuare il
raffreddamento del sensore: allo scopo si può via via operare utilizzando l’effetto Peltier inverso, cicli
Stirling inversi, azoto liquido.
Sulla base delle relazioni scritte, conoscendo i valori dei diversi parametri in gioco, rilevando la
temperatura del sensore si potrebbe risalire alla temperatura della sorgente.
In realtà, viste le applicazioni industriali, si preferisce effettuare una taratura per confronto piuttosto
che ricorrere alle leggi della radiazione.
E’ fondamentale ricordare che la L sorg cui si fa riferimento deve tener conto delle caratteristiche della
sorgente stessa; in altre parole dev’essere conosciuta l’emissività della sorgente (e l’eventuale
dipendenza dalla temperatura) .
Nella tabella di seguito riportata sono alcuni valori di emissività.
I primi sensori di radiazione utilizzati sono state le termopile: le termopile sono costituite da più
termocoppie in serie con giunti caldi su superfici annerite per meglio assorbire le radiazioni incidenti.
Alle termopile hanno fatto seguito le celle fotoelettriche: pur operando queste ultime in bande limitate
di lunghezza d’onda (in particolare della radiazione infrarossa), la sensibilità è nettamente superiore a
quella delle termopile; si parla in questo caso di pirometri a banda piuttosto che di pirometri a
radiazione totale.
Va osservato che mentre quanto riportato per il raffreddamento del sensore dev’essere sempre
applicato alle termopile, nel caso di sensori utilizzanti celle fotoelettriche, la sensibilità delle stesse alle
radiazioni (in particolare infrarosse) può rendere superfluo il raffreddamento dei sensori stessi; il
raffreddamento viene pertanto adottato quando si debba ridurre il rumore di fondo. Nei dispositivi in
commercio, non particolarmente pregiati, la precisione è dell’ordine del °C.
TERMOGRAFIA E TERMOCAMERE
I principi studiati possono essere utilizzati per il rilevamento di mappe di temperatura superficiali
(termografia); allo scopo si può, per esempio, dotare un pirometro a banda di un sistema di scansione a
prismi rotanti posto tra l’ottica del pirometro e il sensore; le prime termocamere sono state realizzate in
questo modo. Alle termocamere a scansione meccanica, si sono affiancate le termocamere a scansione
elettronica; in queste ultime al singolo sensore di radiazione si sostituisce un array di sensori, ciascuno
dei quali è focalizzato su una porzione della superficie da esaminare; mediante la scansione elettronica
si possono rilevare mappe di temperatura a frequenze di centinaia di Hz, (anche del migliaio di Hz),
mentre mediante la scansione meccanica non si supera qualche Hz (al massimo la decina di Hz).
Tra le applicazioni della termografia si ricordano il controllo delle perdite di isolamento negli edifici,
l’individuazione di punti caldi in circuiti elettrici o elettronici, la localizzazione di malfunzionamenti
in meccanismi e apparecchiature meccaniche, la diagnosi precoce di tumori che danno luogo ad
anomalie di temperatura sulla pelle.
In figura , per esempio, è mostrato un esempio di due connessioni elettriche una delle quali si trova a
temperatura più alta dell’altra.
Analogamente, in questa figura è mostrato un supporto in cui uno dei cuscinetti si trova a temperatura
più alta dell’altro.
In entrambi i casi occorre indagare sulle ragioni di tali differenze.