19/11/2011
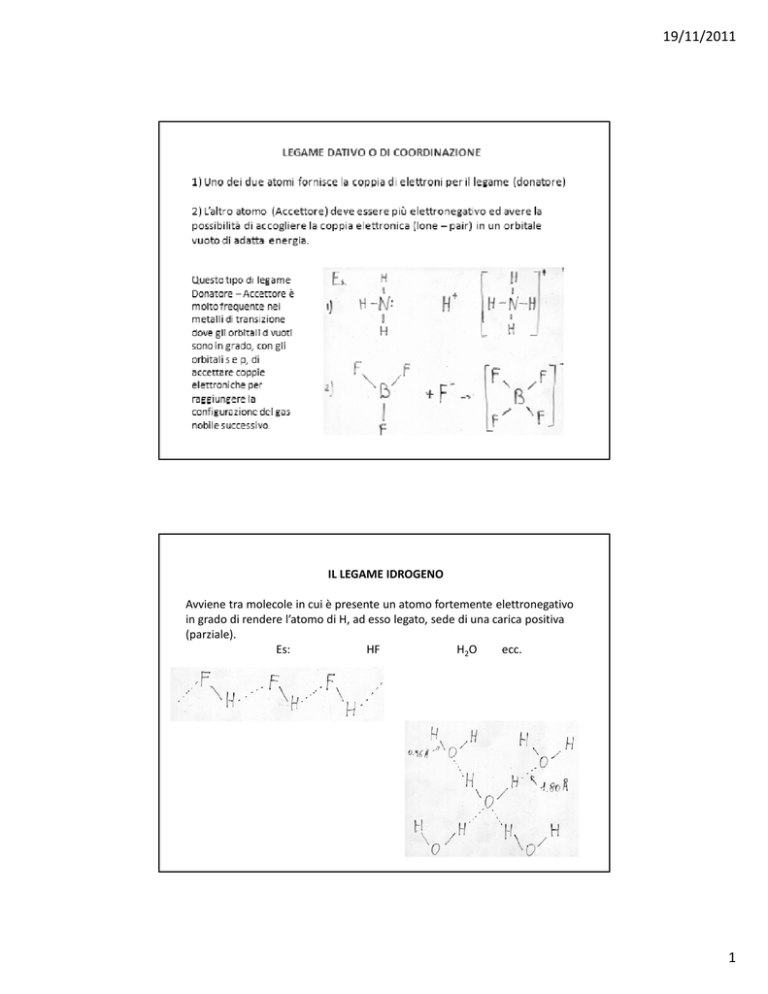
IL LEGAME IDROGENO
Avviene tra molecole in cui è presente un atomo fortemente elettronegativo
in grado di rendere l’atomo di H, ad esso legato, sede di una carica positiva
(parziale).
Es:
HF
H2O
ecc.
1
19/11/2011
La presenza del legame idrogeno intermolecolare comporta una diminuzione
della volatilità e quindi un aumento della temperatura di fusione e di
ebollizione.
Es:
Differenze tra H2O e H2S
H2O
bolle a 100° C
fonde a 0° C
H2S
bolle a –61.8° C
fonde a –85.5° C
L’ordine di grandezza dell’energia associata a questo tipo di legame è di circa
10÷30 kJ ⋅mol-1
FORZE DI VAN DER WAALS
Sono interazioni di natura elettrostatica del tipo:
ione – dipolo
ione – dipolo indotto
dipolo – dipolo
dipolo – dipolo indotto
Es:
K+
in presenza di H2O
Sono legami deboli la cui energia è dell’ordine della decina di kJ ⋅mol-1
2
19/11/2011
TEORIE MODERNE SUL LEGAME COVALENTE
TEORIA DEL LEGAME DI VALENZA
Il legame covalente si forma per sovrapposizione di due orbitali atomici.
1)
2)
3)
4)
3
19/11/2011
ORBITALI IBRIDI
Derivano dal mescolamento di orbitali atomici e sono capaci di formare
legami più forti.
Es:
CH4
ha angoli :
Nessuno degli orbitali atomici del C è orientato rispetto agli altri secondo
questo angolo.
Gli orbitali s p e d di un atomo spesso si mescolano per dare origine a nuovi
orbitali atomici detti orbitali ibridi, nel formare un legame.
Hanno forme e proprietà direzionali nuove.
IBRIDO sp
Ibridizzando un orbitale s ed uno p di uno stesso atomo otteniamo due orbitali
ibridi sp.
I due orbitali sp hanno lo stesso centro e sono orientati:
4
19/11/2011
Es.
BeH2
gassoso:
con H non si può formare un legame
Questi due formano orbitali ibridi sp
Non ibridizzati
IBRIDI sp2
Un orbitale s si combina con due orbitali p: si formano tre orbitali ibridi sp2
Es:
BCl3
Si ibridizzano per formare i tre orbitali ibridi sp2
equivalenti e con la stessa energia
5
19/11/2011
IBRIDI sp3
Derivano dalla combinazione tra un orbitale s e tre orbitali p.
Elettroni spaiati
Si combinano per formare quattro orbitali
ibridi sp3 equivalenti. Sono orientati nello
spazio verso i vertici di un tetraedro.
6
19/11/2011
Es:
C2H6
– Etano –
Un orbitale ibrido per ogni C viene utilizzato per il legame C – C . Tutti gli altri
orbitali sp3 vengono impiegati in legami C – H .
La libera rotazione intorno al legame C – C non influenza il grado di
sovrapposizione dei due orbitali sp3 impegnati nel legame.
Es:
Come spiegare con gli orbitali ibridi il composto SF6?
S
Spaiando tutti gli elettroni:
S
Ibridizzazione sp3d2
S
sp3d2
3d non ibridizzati
Ora si possono formare i sei legami S – F
SF6
7
19/11/2011
FINE
Es:
H2O
angolo 104.5°
Es:
NH3
angolo 107°
O
ibridizzazione e
formazione del legame.
O in H2O
N
ibridizzazione sp3 e formazione legame
N in NH3
H2O
NH3
8
19/11/2011
Le sovrapposizioni di orbitali viste sino ad ora producono legami in cui la densità
elettronica è concentrata tra i nuclei dei due atomi che si legano.
Questo tipo di legame, ottenuto dalla sovrapposizione di orbitali s, p o ibridi
nelle varie combinazioni, è chiamato legame σ (sigma).
a)
b)
c)
Legami σ da orbitali s (a), p (b) e ibridi (c).
Gli orbitali p possono sovrapporsi in altro modo:
Dando luogo a due regioni separate di densità elettronica.
Il legame che si ottiene è chiamato legame π (p – greco).
Es:
C2H4
C
(etilene)
(elettroni spaiati)
Formazione di 3 orbitali ibridi sp2
C
sp2 usati per
formare
legami σ.
2p non
ibridizzato
9
19/11/2011
Si ha sovrapposizione s – sp2 per formare quattro legami σ C – H e sp2 – sp2
per formare un legame σ C – C
Quindi
Etilene:
La rotazione intorno al legame C – C è impedita.
Es:
Etino
C2H2
C
10
19/11/2011
In modo analogo possono essere descritti i modi di legarsi di altre molecole
con tripli legami:
Es:
C
C
C
H
N2
C
C
C
H
1.54 Å
1.34 Å
1.20 Å
0.75 Å
348 kJ/mol
615 kJ/mol
812 kJ/mol
435 kJ/mol
Occorrono 435 kJ per rompere una mol di legami H – H in atomi neutri di H
FINE
11
19/11/2011
TEORIA DEGLI ORBITALI MOLECOLARI
Il metodo consiste nel calcolare le funzioni d’onda molecolari associate a
nuclei considerati in posizione stabile di equilibrio.
Dalla sovrapposizione di orbitali atomici si ottengono gli orbitali molecolari
come combinazione lineare degli orbitali atomici.
La combinazione può essere addittiva o sottrattiva da cui derivano
rispettivamente un orbitale di legame e uno di antilegame.
Il numero totale di orbitali molecolari è uguale al numero totale di orbitali
atomici che hanno contribuito a generarli.
Dalla combinazione lineare di due orbitali s e un orbitale p si
ottengono un orbitale σ di legame ed un orbitale σ∗ di
antilegame a più alta energia.
La molecola non può esistere
12
19/11/2011
Quando si combinano orbitali p possono aversi due casi:
1) Se i lobi sono rivolti l’uno verso l’altro e cioè lungo l’asse internucleare si
formano due orbitali molecolari di tipo σ e σ∗.
2) Se i lobi sono a 90° rispetto all’asse internucleare e si sovrappongono
sopra e sotto tale asse si formano due orbitali molecolari π di legame e
π∗ di antilegame.
Per le molecole biatomiche del secondo periodo:
Le configurazioni elettroniche sono ottenute utilizzando le stesse regole
usate per il riempimento degli orbitali atomici negli atomi.
N° elettroni leganti – N° elettroni antileganti
Ordine di legame =
2
Se è uguale a 0 la molecola non può esistere (es. He2).
13
19/11/2011
ORBITALI MOLECOLARI DELOCALIZZATI
Quando tre o più atomi formano una sequenza continua di sovrapposizione,
gli elettroni condivisi possono essere distribuiti fra più di due atomi.
Secondo la teoria del legame di valenza il benzene può essere descritto in
termini di strutture di risonanza:
I doppi legami indicano la presenza di un legame π tra due atomi di C.
14
19/11/2011
LEGAME METALLICO
1) Gli elementi metallici hanno basse Ei ed Ea. Ciò fa si che abbiano poca
tendenza a formare molecole metalliche omeopolari.
2) Le loro strutture cristalline sono compatte:
ogni atomo è legato ad altri 8 con un reticolo cubico a corpo centrato.
ogni atomo è legato con altri 12 atomi con un reticolo cubico a facce
centrate (o esagonale compatto).
Nessuno dei legami visti fino ad ora è in grado di spiegare queste strutture e le
proprietà dei metalli.
Legame metallico
< è Ei e più è favorita la formazione di tale legame.
La formazione del cristallo è spontanea per cui si ha anche in questo caso una
energia reticolare.
Conducibilità elettrica.
La banda e’
occupata per metà
Se applico ∆V gli elettroni sono liberi di muoversi nella direzione del campo
elettrico applicato.
Conduttore – Semiconduttore – Isolante.
Conducibilità Termica, Lucentezza, Proprietà meccaniche
Spiegabili mediante il modello proposto per il legame metallico.
15
19/11/2011
FINE
NUMERO DI OSSIDAZIONE
Quando un atomo è legato ad un altro atomo essi modificano la loro struttura
elettronica esterna.
Nel caso del legame ionico tale modifica è più evidente rispetto al caso del legame
covalente.
Es:
NaCl
BaCl2
Na+ Cl-
Ba2+
Cl-
In questi casi si dice che il Sodio ha valenza +1, il Cloro –1, ed il Bario +2.
Nel caso di legame parzialmente ionico il valore del numero di ossidazione è assunto
uguale alla valenza che avrebbe l’atomo considerato nel caso che il composto di cui fa
parte fosse ionico, attribuendo la coppia di legame all’elemento più elettronegativo.
δ+
Es:
HCl
δ-
H – Cl
In questo caso si attribuisce la coppia di legame al Cl- che assume numero di ossidazione
–1. H ha numero di ossidazione +1.
16
19/11/2011
Nel caso di molecole formate da atomi uguali questi hanno numero di
ossidazione zero.
Es:
H2
Cl2
O2
ecc.
Un elemento può avere diversi numeri di ossidazione in molecole diverse o
nella stessa molecola.
Il numero di ossidazione indica il numero di elettroni che è necessario dare
(se positivo) o togliere (se negativo) ad un atomo in un composto per portarlo
al numero di ossidazione zero.
Esistono delle regole semplici che permettono di attribuire il numero di
ossidazione agli atomi in un composto senza conoscere il valore dell’
elettronegatività per ognuno di essi:
1) Gli atomi nelle sostanze elementari hanno numero di ossidazione uguale a
zero. (Es: Na, He, O2, Cl2, P4).
2)
L’ossigeno nei composti ha numero di ossidazione = -2.
Fanno eccezione i perossidi (Es: H2O2) in cui ha numero di ossidazione = -1
ed i superossidi, caratterizzati dallo ione O2- dove l’ossigeno ha numero di
ossidazione = -1/2.
3)
L’idrogeno ha numero di ossidazione = +1.
Fanno eccezione gli idruri metallici (Es: NaH, CaH2) dove ha numero di
ossidazione = -1.
4) Il Fluoro ha sempre numero di ossidazione = -1.
5) I metalli alcalini (Li, Na, K, Rb, Cs, Fr) hanno numero di ossidazione = +1.
6) Gli ioni dei metalli alcalino terrosi (Be, Mg, Ca, Sr, Ba, Ra) hanno numero di
ossidazione = +2.
7) Il numero di ossidazione di altri elementi presenti nella molecola viene
calcolato in modo che la somma algebrica dei numeri di ossidazione di tutti
gli atomi del composto sia uguale a zero o , se si tratta di uno ione, sia uguale
alla carica dello ione stesso.
17
19/11/2011
Es:
Numero di ossidazione dello S in H2SO4?
n.o. di H x 2 + n.o. di S + n.o. di O x 4 = 0
+1x2 + n.o. di S + ( -2x4) = 0 da cui: n.o. di S = +6
OSSIDAZIONE – RIDUZIONE
Molte reazioni chimiche comportano il trasferimento di densità elettronica
da un atomo ad un altro.
Es:
1)
2 Na
+
Cl2
→
2 NaCl
2)
2 H2
+
O2
→
2 H2O
In 1) (formazione di ioni) si è avuto sicuramente un trasferimento di
densità elettronica da Na a Cl.
In 2) è meno evidente, ma la polarità della molecola (O2 è più
elettronegativo di H) evidenzia che comunque c’è stato un trasferimento di
densità elettronica verso l’ossigeno.
Tali reazioni sono chiamate reazioni di ossido – riduzione o reazioni redox:
la specie che perde elettroni si ossida.
la specie che acquista elettroni si riduce.
Non può esistere una reazione di sola ossidazione o di sola riduzione.
La specie A che cede elettroni alla specie B è l’agente riducente. La
specie B è l’agente ossidante.
il numero di elettroni persi dal riducente è uguale al numero di elettroni
acquistati dall’ossidante.
in particolari reazioni, dette di dismutazione o disproporzione o di
ossidoriduzione interna, la stessa specie chimica in parte si riduce ed in
parte si ossida dando luogo a specie differenti.
18
19/11/2011
Sostanze ossidanti e riducenti cosa sono?
Scala delle varie specie:
spiccate proprietà
riducenti
spiccate proprietà
ossidanti
Cioè, scendendo lungo la scala aumenta il potere ossidante.
Es:
a HI + b Cl2 + c H2O
→
d HCl + f HIO3
a, b, c, d, f da determinare basandosi sulle variazioni dei numeri di
ossidazione.
Vediamo il procedimento:
1. si individua la specie ossidante e la specie riducente.
2. si calcola in numero di elettroni acquistati, n1, da una formula dell’ossidante, ed il
numero di elettroni ceduto, n2, da un formula del riducente.
Nell’esempio
Cl2 + 2 e- → 2 Cl-
n1 ossidante
→ I5+ + 6 e-
n2 riducente
I-
3. n2 viene preso come coefficiente della specie ossidante ed n1 della specie
riducente.
Nell’esempio per ogni I- che si ossida, si riducono 6 atomi di Cl cioè 3 Cl2
(a = 1 ; b = 3).
4. stabiliti i coefficienti dell’ossidante e del riducente, seguono i coefficienti del
prodotto di riduzione dell’ossidante e del prodotto di ossidazione del riducente.
Nell’esempio
(d = 6 ; f = 1)
5. si bilanciano le masse: tutti gli atomi che compaiono a sinistra debbono ritrovarsi a
destra. (in genere basta bilanciare H e O).
Nell’esempio
(c = 3)
19
19/11/2011
USO DELLE SEMIREAZIONI
Fe3+
Es. 1)
+
Sn2+
→
ossidazione
Sn2+ → Sn4+
riduzione
Fe3+ → Fe2+
Fe2+ + Sn4+
reazione in cui sono
riportati solo gli ioni interessati
(FeCl3 + SnCl2)
Si bilanciano prima le masse (sono già bilanciate) e poi le cariche:
Sn2+ → Sn4+ + 2 eFe3+ + e- →
Fe2+
Il numero di elettroni persi è sempre uguale al numero di elettroni acquistati.
Sn2+ →
Sn4+ + 2 e-
2.( Fe3+ + e- →
Sn2+ →
Fe2+ )
cioè:
Sn4+ + 2 e-
2 Fe3+ + 2 e- → 2 Fe2+
Sommando le semireazioni abbiamo la reazione bilanciata:
2 Fe3+ + Sn2+ + 2 e- → Sn4+ + 2 Fe2+ + 2 e-
E’ importante sapere se la reazione avviene in ambiente acido o basico.
Es:
Cr2O72- + Fe2+ → Cr3+ + Fe3+
in ambiente acido
Fasi da percorrere per il bilanciamento:
1.
dividere l’equazione in semireazioni
2.
bilanciare gli atomi diversi da H e O
3.
bilanciare O aggiungendo H2O
4.
bilanciare H aggiungendo H+
5.
bilanciare la carica aggiungendo e-
6.
eguagliare e- acquistati e ceduti. Sommare le semireazioni.
7.
Cancellare ciò che risulta uguale in entrambe le parti.
20
19/11/2011
1)
Cr2O72- →
Cr3+
→
Fe3+
Fe2+
2)
Cr2O72- →
Fe2+
3)
Fe3+
Cr2O72- → 2 Cr3+ + 7 H2O
Fe2+
4)
→
2 Cr3+
→
Fe3+
14 H+ + Cr2O72- → 2 Cr3+ + 7 H2O
→
Fe2+
5)
14 H+ + Cr2O72-
Fe3+
→ 2 Cr3+ + 7 H2O
(14+) + (2-) =12+
2 (3+) = 6+
6 e- + 14 H+ + Cr2O72- → 2 Cr3+ + 7 H2O
Fe2+
5)
→ Fe3+ + e-
14 H+ + Cr2O72(14+) + (2-) =12+
→ 2 Cr3+ + 7 H2O
2 (3+) = 6+
6 e- + 14 H+ + Cr2O72- → 2 Cr3+ + 7 H2O
Fe2+
6)
6 e- + 14 H+ + Cr2O72- → 2 Cr3+ + 7 H2O
6 ( Fe2+
somma:
→ Fe3+ + e-
→ Fe3+ + e- )
6 e- + 14 H+ + Cr2O72- + 6 Fe2+ → 2 Cr3+ + 7 H2O + 6 Fe3+ + 6 e-
7) 14 H+ + Cr2O72- + 6 Fe2+ → 2 Cr3+ + 7 H2O + 6 Fe3+
Reazione bilanciata
21
19/11/2011
In ambiente basico, una volta arrivati al punto 7. si procede oltre:
8.
aggiungere de entrambe le parti un numero di OH- corrispondente a
quello degli H+
9.
trasformare OH- e H+ in H2O
10. eliminare H2O per quanto è possibile
Es:
SO32- + MnO4- → SO42- + MnO2
in ambiente
basico
FINE
22
19/11/2011
TERMODINAMICA CHIMICA
La termodinamica è lo studio delle variazioni energetiche e del trasferimento
di energia da una sostanza ad un’altra.
Consente quindi di prevedere se una reazione, in certe condizioni
sperimentali, può avvenire o meno.
Non dà però nessuna indicazione sul meccanismo o sulla velocità con cui
avviene.
Sistema termodinamico: è costituito almeno da una porzione percettibile di
materia. Solitamente è costituito da un insieme macroscopico, omogeneo o
eterogeneo, di corpi.
Un sistema può essere:
isolato, quando non può scambiare con l’esterno né materia né energia;
chiuso, quando può scambiare solo energia;
aperto, quando può scambiare energia e materia.
Lo stato di un sistema è descritto quando si conoscono i valori del numero
minimo di parametri che definiscono univocamente il sistema (variabili di
stato).
La variazione di una o più variabili di stato, causata dal passaggio del sistema
da uno stato (a) ad uno stato (b), non dipende dal cammino percorso durante
la trasformazione, ma solo dallo stato iniziale (a) e da quello finale (b).
Le variabili di stato possono essere:
Estensive: se dipendono dalle dimensioni del sistema (es: volume, n° di
moli). Sono additive.
Intensive: cioè indipendenti dalle dimensioni del sistema (es: temperatura,
pressione). Non sono additive.
Per lo studio di un sistema termodinamico è importante che la variabili di
stato siano riferite al sistema in equilibrio.
23
19/11/2011
I° PRINCIPIO DELLA TERMODINAMICA
L’energia può essere convertita da una forma in un’altra, ma non può essere
né creata né distrutta.
Ogni sistema è caratterizzato da un valore U della propria energia interna.
U rappresenta la somma di tutte le energie del sistema legate al suo stato e
non può essere determinato.
Ciò che interessa sono le differenze tra i valori di U del sistema presi prima e
dopo una trasformazione.
Perché U possa variare il sistema non deve essere isolato.
U può essere scambiata con un mezzo meccanico (mediante lavoro) o con
scambio di calore se esiste una differenza di temperatura tra sistema e
ambiente.
1) Calore scambiato dal sistema con l’esterno. E’ considerata positiva la
quantità di calore acquistata dal sistema; negativa quella perduta.
2) Lavoro scambiato dal sistema con l’esterno. E’ considerato negativo il
lavoro che il sistema compie sull’esterno e positivo quello compiuto
dall’esterno sul sistema.
Se un sistema non isolato passa da uno stato (a), con energia Ua, ad uno
stato (b), con energia Ub, ha scambiato energia.
∆U = Ub – Ua
Indicando con Q e L il calore ed il lavoro scambiati, in base a 1) e 2)
possiamo scrivere:
∆U = Q + L
cioè la variazione di energia è pari alla somma tra calore e lavoro scambiati
con l’esterno.
U è una funzione di stato (non dipende dal percorso per andare da (a) a (b)).
24
19/11/2011
Q ed L singolarmente dipendono dal cammino percorso. E’ solo la loro
somma (Q + L) che resta costante.
Durante l’espansione il gas non assorbe né cede calore; T si mantiene
costante, quindi Q = 0. Inoltre non c’è variazione di volume con l’esterno
quindi L = 0 per cui ∆U = 0.
Ne consegue che:
L’energia interna di un gas ideale non dipende né dal volume occupato né
dalla pressione, ma solo dalla temperatura.
P esterna
Il lavoro compiuto in questa
trasformazione è:
L = - P ∆V
Newton
V2
V1
m2
dove: ∆V = V2 – V1
.m
3
N.m
dim. Lavoro
Il primo principio espresso da :
∆U = Q + L
può essere applicato a reazione che avvengono:
a pressione costante:
∆U = Qp – P ∆V
(I)
a volume costante:
∆U = Qv
la (I) può essere scritta:
U2 – U1 = Qp – P (V2 – V1)
(U2 + PV2) – (U1 + PV1) = Qp
(II)
La quantità U + PV è una funzione di stato dato che U, P e V sono funzioni o
variabili di stato.
H = U + PV
= entalpia
Pertanto la (II) può essere scritta:
∆H = Qp
∆H è la quantità di calore scambiato con l’esterno a
P costante.
25
19/11/2011
Abbiamo visto che
quindi:
H = U + PV
∆H = ∆U + V∆P + P∆V
A volume costante ∆V = 0 e ricordando che ∆U = Qv
∆H = Qv + V∆P
dall’equazione di stato dei gas:
a T e V costanti si può scrivere:
PV = n RT
∆P = ∆n RT/V
∆H = Qv + ∆n RT
che consente di calcolare ∆H noti Qv (determinabile con un calorimetro) e ∆n.
I valori di ∆H determinati a P costante e a V costante per una stessa reazione
hanno valori molto simili e coincidono per reazioni che no comportano
variazioni di volume.
Il valore di ∆H di una reazione che avviene a P o a V costanti è indipendente dal
cammino secondo cui la reazione avviene, e dipende solo dallo stato iniziale
(reagenti) e dallo stato finale (prodotti).
- Legge di Hess. -
FINE
26
19/11/2011
Entalpia molare di formazione:
è il ∆H di una reazione che parte dagli elementi e porta alla formazione di una
mole di composto:
si indica con ∆Hf
il valore di H dipende dalla T e dalla P.
Quindi, in condizioni standard ( 1 atmosfera, 25°C):
∆Hf°
se entalpia di formazione di composti dagli elementi
∆H°
se entalpia di reazione
Si definisce stato standard di una specie chimica quello della specie allo stato
puro, alla pressione di una atmosfera ed alla temperatura di 25° C.
- Definire di ∆Hf° I valori di ∆Hf° degli elementi sono = 0. Essi devono trovarsi nello stato
molecolare e di aggregazione in cui sono stabili a 25° C ed alla P = 1 atm.
Per convenzione: ∆Hf° dello ione H+ in soluzione acquosa è = 0 ed a esso
vengono riferiti i valori delle altre specie ioniche.
Quando si sommano equazioni termochimiche per dare nuove equazioni, i
valori dei loro ∆H si sommano anche essi per dare il valore del ∆H della nuova
equazione.
Es:
C(s) + O2(g) → CO2(g)
∆H° = -94.05 kcal = -393.5 kJ
C(s) + ½ O2(g) → CO(g)
∆H° = -26.42 kcal = -110.5 kJ
CO(g) + ½ O2(g) → CO2(g)
∆H° = -67.63 kcal = -283.0 kJ
Oppure:
-94.05 = (-26.42) + (-67.63)
Permette di calcolare i ∆H° di una reazione noti gli altri valori.
Il ∆H di una reazione può essere ottenuto dalla sottrazione della somma dei
calori standard di formazione dei reagenti dalla somma dei calori standard di
formazione dei prodotti, ciascuno moltiplicato per il rispettivo coefficiente
stechiometrico. E’ il modo di applicare la legge di Hess.
27
19/11/2011
Il valore di ∆H° per una reazione è indipendente dal cammino percorso, ma
dipende solo dallo stato iniziale e finale del sistema.
Si può misurare ∆H° come se la reazione avvenisse in uno stadio, oppure seguire
strade diverse e fare la somma dei vari ∆H°.
Es:
SO3(g) → SO2(g) + ½ O2(g)
Dalle tabelle ∆Hf° per SO3 = -94.45 kcal/mol
Si può immaginare che:
∆H° = ∆H°decompos. reag. + ∆H°formaz. Prod.
Ma:
∆H°decompos. reag. = - ∆H°formaz. reag.
per cui:
∆H° = - ∆H°formaz. reag. + ∆H°formaz. prod.
Cioè:
∆H° = ∆H°formaz. prod. - ∆H°formaz. reag.
Cioè:
∆H °( reazione ) = ∑ i ∆H f °( prodotti ) − ∑ i ∆H f °( reagenti )
( Legge di Hess)
Es:
C(s) + 2H2(g) → CH4(g)
∆H°f (CH4)?
1)
CH4(g) + 2O2(g) → CO2(g) + 2H2O(l)
∆H° = -890.36 kJ
2)
C(s) + O2(g) → CO2(g)
∆H° = ∆H°f(CO2) = -393.5 kJ
3)
H2(g) + ½ O2(g) → H2O(l)
∆H° = ∆H°f (H2O) = -285.85 kJ
non determinabile
∆H°f (CH4) = 2) + 2. 3) – 1)
∆H°f (CH4) = -393.5 + (2⋅(-285.85)) - (-890.36) = -74.84 kJ
28
19/11/2011
∆H° per la reazione:
Es:
4 NH3(g) + 5 O2(g) → 4 NO(g) + 6 H2O(g)
∆H°reaz. = (4 ∆H°f (NO)(g) + 6 ∆H°f (H2O)(g) ) – (0 + 4 ∆H°f (NH3)(g) )=
∆H°reaz. = -904.8 kJ
reazione esotermica.
ENERGIA DI LEGAME E SUA MISURA
L’energia di legame ha grande influenza sulle proprietà chimiche delle sostanze.
L’energia di legame è la quantità di energia necessaria per rompere il legame
chimico per formare frammenti elettricamente neutri.
Indica, per esempio, se nella molecola ci sono singoli, doppi o tripli legami.
(l’E. di legame aumenta col numero di legami).
Es:
C – C
1.54 Å
348 kJ/mol
C
C
1.34 Å
615 kJ/mol
C
C
1.20 Å
812 kJ/mol
Durante le reazioni chimiche alcuni legami si rompono mentre altri si formano.
Il primo stadio (la rottura) è uno dei fattori che controllano la reattività.
Es:
N2
ha un triplo legame N
N molto forte. Legami forti
possiedono elevata energia di legame. E’ difficile rompere il legame azotoazoto per cui N2 è una molecola poco reattiva.
29
19/11/2011
Dallo spettro di emissione di molecole semplici (H2, O2, Cl2 ecc.) si ottengono
informazioni sui livelli energetici della molecola da cui vengono calcolate le
energie di legame.
Per molecole più complesse si usano dati termochimici.
Energia di atomizzazione (∆Hatom) = energia necessaria per rompere tutti i
legami chimici presenti in una mole di molecole gassose.
Es:
CH4(g) → C(g) + 4 H(g)
CH4
Dividendo il ∆Hatom per 4 si otterrà l’energia media del legame C – H nel
metano.
Per il calcolo può essere usato il ∆Hf° infatti:
C(g) + 4 H(g)
2↑
1↑
C(s) + 2 H2(g)
3
→ CH4(g)
∆Hf°
dato che H è una funzione di stato le variazioni sono indipendenti dal
cammino percorso.
Le variazioni di entalpia dei processi 1 e 2 sono chiamate calori standard di
formazione degli atomi gassosi.
Questi valori sono stati calcolati e tabulati.
Il processo 3 è l’opposto dell’atomizzazione e la sua variazione entalpica
corrisponderà a - ∆Hatom.
2 H2(g) → 4 H(g)
C(s)
→ C(g)
4 H(g) + C(g) → CH4(g)
∆H1° = 4 ∆Hf° (H(g))
∆H2° = ∆Hf° (C(g))
∆H3° = - ∆Hatom
a) 2 H2(g) + C(s) → CH4(g)
∆H° = ∆Hf° (CH4(g))
a) = reazione di formazione del CH4 dai suoi elementi nello stato standard,
quindi sommando i loro ∆H° si otterrà ∆Hf° per CH4 :
∆H1° + ∆H2° + ∆H3° = ∆Hf° (CH4(g)) cioè:
∆Hf° (H(g)) = 218.0 kJ/mol
∆Hf° (C(g)) = 715.0 kJ/mol
4 ∆Hf° (H(g)) + ∆Hf° (C(g)) + (-∆Hatom) = ∆Hf° (CH4(g)) ∆Hf°(CH4(g)) = -74.8 kJ/mol
per cui:
∆Hatom = 1662 kJ/mol
dividendo per 4 si ottiene:
1662 /4 = 416 kJ/mol = energia media del legame C – H nel CH4.
30
19/11/2011
FINE
31










