Attraversamento di un albero (binario)

Attraversamento di un albero (binario)
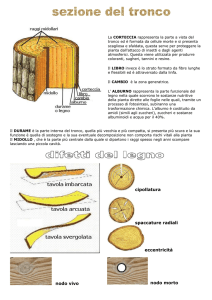
1) Preordine
Algorithm binaryPreorder( T, v) //caso di albero binario
Visita il nodo v;
Se v è un nodo interno allora
binaryPreorder( T, T.leftChild(v)); //Attraversamento ricorsivo sottoalbero sinistro
Se v è un nodo interno allora
binaryPreorder( T, T.rightChild(v)); //Attraversamento ricorsivo sottoalbero destro
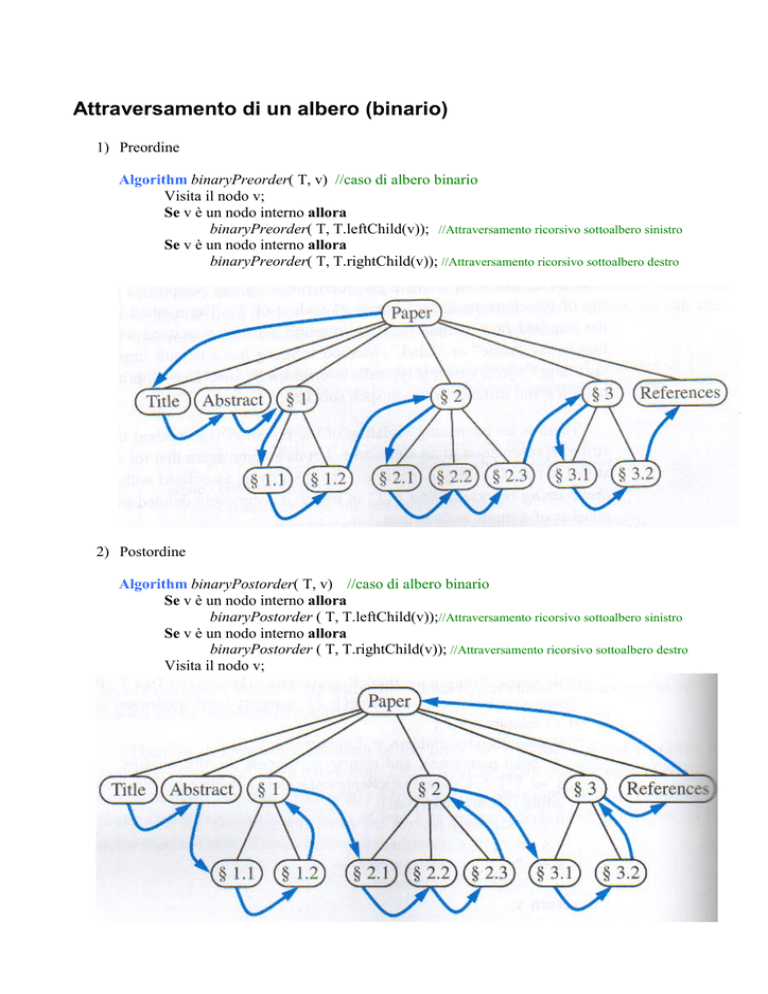
2) Postordine
Algorithm binaryPostorder( T, v) //caso di albero binario
Se v è un nodo interno allora
binaryPostorder ( T, T.leftChild(v));//Attraversamento ricorsivo sottoalbero sinistro
Se v è un nodo interno allora
binaryPostorder ( T, T.rightChild(v)); //Attraversamento ricorsivo sottoalbero destro
Visita il nodo v;
3) Inordine
Algorithm binaryInorder( T, v) //caso di albero binario
Se v è un nodo interno allora
binaryInorder ( T, T.leftChild(v)); //Attraversamento ricorsivo sottoalbero sinistro
Visita il nodo v;
Se v è un nodo interno allora
binaryInorder ( T, T.rightChild(v)); //Attraversamento ricorsivo sottoalbero destro
I tre tipi di attraversamento sono definibili tramite delle procedure che sono molto simili. A questo
punto è possibile scrivere una procedura comune che unisce le tre procedure appena scritte…
Î EULER TOUR (attraversamento di Eulero)
Algorithm eulerTour( T, v) //caso di albero binario
Visita il nodo v; //visita dalla sinistra
Se v è un nodo interno allora
//Attraversamento ricorsivo sottoalbero sinistro
eulerTour ( T, T.leftChild(v));
Visita il nodo v; //visita dal basso
Se v è un nodo interno allora
eulerTour ( T, T.rightChild(v)); //Attraversamento ricorsivo sottoalbero destro
Visita il nodo v; //visita dalla sinistra
Ogni nodo dell’albero viene visitato tre volte.
A seconda del tipo di visita che viene svolta su un nodo è possibile ottenere degli algoritmi
specialistici, che compiono determinate azioni come il calcolo di una espressione numerica su di un
albero binario come quello riportato in figura. Oppure è possibile creare, attraverso l’algoritmo di
attraversamento Inordine una procedura che calcoli le coordinate di ogni nodo per una
rappresentazione grafica di un albero.
Esempio:
Algorithm disegnaAlbero( T, v, livello) //caso di albero binario
Se v è un nodo interno allora
disegnaAlbero ( T, T.leftChild(v), livello+1);//chiamata ricorsiva sottoalbero sinistro
Disegna_nodo(v, num_nodo++, livello) // Visita il nodo v; //visita
Se v è un nodo interno allora
disegnaAlbero(T,T.rightChild(v), livello+1); //chiamata ricorsiva sottoalbero destro
int num_nodo = 0;
disegnaAlbero( T, T.root(), 0) //caso di albero binario
L’esempio mostra come siano necessarie altre variabili per permettere l’elaborazione della
procedura. Tuttavia la procedura mostrata ricalca perfettamente l’algoritmo di attraversamento di un
albero Inordine.
Viene da pensare che sia possibile utilizzare l’algoritmo di attraversamento di Eulero per formulare
una procedura generale. Quindi tutte le procedure che sfruttano qualche metodo sistematico di
attraversamento di una labero binario potrebbero essere ‘inscatolate’ in un algoritmo generale da
affinare in modo diverso a seconda degli scopi. Æ template method pattern
Template method pattern
Il template method pattern descrive un meccanismo generico di elaborazione che può essere
facilmente adattato per una particolare applicazione.
Naturalmente per poter ‘descrivere’ un metodo generale adattabile a seconda dei casi è necessario
dotarsi di un contenitore per la memorizzazione di alcune variabili durante la ‘visita’ all’albero.
Tale contenitore è un array di tre elementi di tipo Object. Metodi aggiuntivi particolari (initResult,
returnResult) serviranno alla creazione, inizializzazione e gestione di tale contenitore.
La procedura generale avrà tre metodi visitLeft, visitBelow e visitRight che corrispondono
rispettivamente ai metodi di ispezione dei nodi nelle procedure di attraversamento Preordine,
Inordine e Postordine.
In più il metodo visitExternal corrisponde al metodo di visita di un nodo nel caso di nodo esterno.
Questa è una delle differenze principali dell’algoritmo di attraversamento di Eulero, dato che in
questo caso le azioni da compiere nel caso il nodo sia esterno o meno sono diverse.
L’algoritmo può essere così descritto:
Algorithm templateEulerTour( T, v)
r[0] = initResult();
Se v è un nodo esterno allora
//visita nodo esterno
r[0] = visitExternal ( T, T.leftChild(v));
altrimenti
visitLeft(T, v, r);
//visita nodo interno sinistro
r[1] = templateEulerTour(T, T.leftChild(v)); //chiamata ricorsiva
visitBelow(T, v, r) ; //visita nodo interno dal basso
r[2] = templateEulerTour(T, T.rightChild(v)); //chiamata ricorsiva
visitRight(T, v, r) ; //visita nodo interno destro
ritorna returnResult(r) ;
Nella pagina seguente è riportato il codice generale dell’algoritmo.
Bisogno notare come gli oggetti memorizzati nell’array r[] di tre elementi siano generati dalla classe
‘TraversalResult’ che contiene i campi finalResult, leftResult e rightResult.
La classe è di tipo astratto perché contiene molti metodi privi di implementazione.
Infine va posta attenzione al metodo execute che è quello che contiene la chiamata al metodo
ricorsivo
eulerTour(T, T.root())
/**
* Template for algorithms traversing a binary tree using an Euler
* tour. The subclasses of this class will redefine some of the
* methods of this class to create a specific traversal.
*/
public abstract class EulerTour {
protected InspectableBinaryTree tree;
public Object execute(BinaryTree T) {
tree = T;
return null; // nothing interesting to return
}
protected Object eulerTour(Position p) {
TraversalResult r = initResult();
if (tree.isExternal(p)) {
visitExternal(p, r);
} else {
visitLeft(p, r);
r.leftResult = eulerTour(tree.leftChild(p)); // recursive traversal
visitBelow(p, r);
r.rightResult = eulerTour(tree.rightChild(p)); // recursive
traversal
visitRight(p, r);
}
return result(r);
}
// methods that can be redefined by the subclasses
protected void visitExternal(Position p, TraversalResult r)
{}
protected void visitLeft(Position p, TraversalResult r)
{}
protected void visitBelow(Position p, TraversalResult r)
{}
protected void visitRight(Position p, TraversalResult r)
{}
protected TraversalResult initResult()
{
return new TraversalResult();
}
protected Object result(TraversalResult r)
{
return r.finalResult;
}
}
La classe può essere ridefinita per esempio per calcolare delle espressioni, come nel frammento di
codice 6.24:
/**
* This traversal specializes EulerTour to compute the
* value of an arithmetic expression stored in the tree. It assumes
* that the elements stored at the external nodes are Integer objects
* and that the elements stored at the internal nodes are of type
* OperatorInfo, supporting method operation(Integer x, Integer y), which
* returns the result of applying an arithmetic operation to x and y.
*/
public class EvaluateExpressionTour extends EulerTour {
public Object execute(BinaryTree T) {
super.execute(T); // calls method of superclass
System.out.print("The value is: ");
System.out.println(eulerTour(tree.root())); //chiamata eulerTour
return null; // nothing interesting to return
}
protected void visitExternal(Position p, TraversalResult r) {
r.finalResult = (Integer) p.element();
}
protected void visitRight(Position p, TraversalResult r) {
OperatorInfo op = (OperatorInfo) p.element();
r.finalResult = op.operation((Integer) r.leftResult,
(Integer) r.rightResult);
}
}