Appunti di
meccanizzazione
forestale
Prof. Andrea Colantoni
MECCANICA E
MECCANIZZAZIONE
MECCANICA
ASPETTI
ingegneristico
qualitativo
ambientale
FINALITA’ - studio delle macchine
in funzione:
della destinazione
della composizione
del principio di funzionamento
del modo di operare in campo
delle prestazioni
MECCANIZZAZIONE
PROBLEMATICHE
scelta delle macchine
utilizzazione delle macchine
OBIETTIVI - ottimizzazione
dell’impiego in funzione:
dell’ambiente
della capacità di lavoro
della tempestività
della manodopera disponibile
dell’impegno finanziario
della convenienza economica
ALFABETO GRECO E SIMBOLOGIA
Αα
Alfa
Ββ
Beta
Angoli piani
Ηη
Eta
Νν
Ni
Θθ
Teta
Ξξ
Ιι
Iota
Κκ
Cappa
Rendimento
Ττ
Tau
Csi
Υυ
Ipsilon
Οο
Omicron
Φφ
Fi
Ππ
Pi
Χχ
Chi
Ψψ
Psi
Ωω
Omega
Viscos. cinematica
Sforzo tangenziale
Angoli piani
Γγ
Gamma
∆δ
Delta
Peso volumico
Incremento finito
Increm. infinitesim.
Epsilon
Εε
Ζζ
Zeta
Angolo di rotazione
Angolo piano
Λλ
Lambda
Μ µ
Mi
Ρρ
Ro
Σσ
Sigma
Massa volumica
Viscos. dinamica
Micro
Sommatoria
Sforzo normale
Ohm
Velocità angolare
SISTEMA INTERNAZIONALE
GRANDEZZE FONDAMENTALI
•
Angolo piano
rad
•
Angolo solido
sr
•
Lunghezza
m
•
Tempo
s
•
Massa
kg
•
Temperatura
°C
•
Corrente elettrica
A
•
Intensità luminosa
cd
•
Quantità di sostanza mol
MULTIPLI
da 101
deca
h 102
etto
k 103
chilo
M 106
mega
G 109
giga
T 1012 Tera
P 1015 Peta
E 1018 Exa
SOTTOMULTIPLI
d
10-1 deci
c
10-2 centi
m
10-3 milli
µ
10-6 micro
n
10-9 nano
p
10-12 pico
f
10-15 femto
a
10-18 atto
Nelle grandezze derivate non deve essere usato l’aggettivo “specifico” ma termini analitici esplicativi:
no “massa specifica” o “densità“; sì “massa volumica”; no “calore specifico”; sì “capacità termica
massica”.
Consentito: t (tonnellata al posto di Mg); ha (ettaro al posto di 10.000 m2); L (litro al posto di dm3);
°(grado sessagesimale: 180°= π rad); h (ora); min (minuto).
Non consentito nelle unità di misura derivate il grado centigrado (°C) ma il grado assoluto (K)
(TA = TC + 273,15). m3°C , per esempio, può generare confusione.
RICHIAMI DI MECCANICA APPLICATA
ALLE MACCHINE
FISICA: lo studio dei fenomeni fisici, quelli che non sono attinenti alla vita
(biologia) e che non alterano permanentemente la costituzione dei corpi
(chimica).
MECCANICA: quella parte della fisica che studia il moto dei corpi (cinematica
e dinamica) e il loro equilibrio (statica).
GRANDEZZA FISICA: qualsiasi entità misurabile e caratterizzata da un valore
numerico e da un’appropriata unità di misura.
MISURA: sottintende un metodo e uno strumento adatto e, soprattutto, la
riproducibilità della stessa nello spazio e nel tempo.
- diametro interno di un cilindro o “alesaggio” d
- superficie del cerchio di base S = π d2 /4
- volume del cilindro V = S x h
Es.: d=100 mm; h=110 mm.
S=7854 mm2; V=864 cm3
GRANDEZZE FISICHE SCALARI: sono caratterizzate solo da un valore
numerico e dalla rispettiva unità di misura (lunghezza, superficie, volume,
massa, temperatura, viscosità, lavoro, potenza...)
Alcune grandezze fisiche sono caratterizzate solo da un valore numerico:
NUMERI PURI o GRANDEZZE ADIMENSIONALI (angolo piano o solido,
coefficiente di resistenza aerodinamica - Cx -, coefficienti di attrito e di
rotolamento...)
GRANDEZZE FISICHE VETTORIALI: sono caratterizzate da un valore
numerico (“modulo”), da una unità di misura, da una direzione e da un verso
(velocità, accelerazione, forza, momento di una forza, coppia...)
Es.: FORZA PESO
P=mg
g=9,806650... m/s2 (a 45°lat. e a l.m.m.)
direzione N-S
verso da Sud a Nord
Vettori applicati: per i corpi deformabili non si può prescindere dal punto di
applicazione della forza. In questo caso le forze vanno considerate come
vettori applicati ad un punto. Nel caso di corpi rigidi (o assimilabili) questo non
è necessario.
CINEMATICA
Studio del moto indipendentemente dalle cause che lo
determinano.
VELOCITA’ (tangenziale): in via semplificata è lo spazio percorso nell’unità
di tempo.
Grandezza vettoriale: direzione tangente alla traiettoria e verso quello di
avanzamento.
1 m/s = 3,6 km/h
Unità di misura di base: m/s
(o ms-1)
ACCELERAZIONE: variazione della velocità nell’unità di tempo.
Grandezza vettoriale: si decompone in due componenti:
- accelerazione tangenziale: come la velocità;
- accelerazione normale (o radiale o centripeta): ortogonale alla precedente
e “verso” verso il centro di curvatura della traiettoria
(in un moto rettilineo si ha solo l’accelerazione tangenziale)
Unità di misura di base: m/s2 (o ms-2)
Moto circolare uniforme:
v (tangenziale) sempre costante in modulo, ma
variabile in direzione e verso
accelerazione solo normale (centripeta)
Si definisce velocità angolare (ω) l’angolo descritto nell’unità di tempo
Unità di misura = rad/s
Direzione: ortogonale al piano di rotazione
Verso: quello da cui si vede avvenire il moto in senso antiorario
Accelerazione centripeta:
ac = ω2 r = v2/r
v=ωr
Es.: Orologio
v = velocità tangenziale
r = raggio
velocità angolare lancetta dei minuti:
ωm = 2π/h = 6,28 rad/h
velocità angolare lancetta delle ore:
ωh = 2π/12h = 0,52 rad/h
- direzione ortogonale al piano dell’orologio;
- verso: quello che va dal quadrante verso l’interno.
Es.: Albero motore che ruoti a 2000 giri/min: ω = 2π x 2000 /60 = 209 rad/s
DINAMICA
Studio delle cause che determinano il moto dei corpi
Primo, seconda e terza legge di Newton
FORZA = massa x accelerazione
F=m.a
Grandezza vettoriale: direzione e verso quelli dell’accelerazione risultante
Unità di misura: newton (N)
(forza che, applicata ad un chilogrammo massa, ne determina l’accelerazione di 1 m/s2)
Relazione tra massa e forza peso:
Fp = mg
(g = accelerazione di gravità)
g è variabile, quindi Fp variabile con g
Se si considera l’accelerazione di gravità “normale” (g = 9,81 m/s2) il peso di un
chilogrammo di massa è:
Fp = 1 kg x 9,81 m/s2 = 9,81 N
Nel sistema “pratico” di unità di misura (abolito dal Sistema Internazionale) l’unità
fondamentale è il chilogrammo peso o forza (kgp o kgf): il peso del chilogrammo massa
sottoposto all’accelerazione di gravità “normale”: 1 kgp = 9,81 N
ma si può anche affermare che un chilogrammo massa “pesa”, in condizioni “normali”,
1 kgp.
MASSA VOLUMICA (ρ): massa dell’unità di volume della sostanza considerata.
Grandezza scalare
Unità di misura: kg/m3
Per l’acqua: ρ = 1.000 kg/m3 = 1 kg/dm3 = 1 kg/L (anche se ρ varia con la temperatura)
PESO VOLUMICO (γ): peso dell’unità di volume della sostanza considerata.
γ=ρg
(g = accelerazione di gravità)
Grandezza scalare
Unità di misura: N/m3
Per l’acqua: γ = 1.000 kgp/m3 x 9,81 m/s2 = 9.810 N/m3
PRESSIONE (p): forza esercitata sull’unità di superficie.
p = f/S
Grandezza scalare
Unità di misura: N/m2 = Pa (pascal)
1 kgp/cm2 = 9,81 N x 104 m-2 = 98.100 Pa = 98 kPa
1 atm = 1,033 kgp/cm2 = 101.000 Pa = 101 kPa (N.B.: atm non S.I.)
1 bar = 100 kPa (per definizione)
Pressione in un liquido: p = ρgh
(h = battente per il punto considerato)
- uguale in ogni direzione (distribuzione idrostatica); normale alla superficie considerata;
sempre di compressione.
COMPOSIZIONE E SCOMPOSIZIONE DI
VETTORI
MACCHINA
Qualsiasi dispositivo fisico in grado di ampliare le capacità
umane (orologio; macchina da scrivere; computer;
televisore; frigorifero; automobile; trattore).
{
- come finalità utile
Eu - come calore utile (generatori di calore...)
- come energia meccanica utile
Ei = Energia (o fonte energetica) in ingresso
Eu = Finalità o Energia utile
Ed = Energia degradata (calore a bassa
temperatura)
In senso termodinamico o solo meccanico: un qualsiasi
dispositivo fisico in grado di convertire una fonte
energetica in ENERGIA MECCANICA o solo di trasmettere
dell’ENERGIA MECCANICA.
MACCHINE
MACCHINA SEMPLICE: dispositivo costituito da un solo organo (leva,
carrucola - paranco -, cuneo, piano inclinato). Le macchine semplici riducono
la forza motrice necessaria a compiere un certo lavoro utile (ma il lavoro
rimane sempre uguale).
MACCHINA COMPOSTA: dispositivo costituito da un insieme di organi
mutualmente vincolati.
MACCHINA (COMPOSTA) MOTRICE O MOTORE: quella che fornisce lavoro
motore (forza motrice) o prevalentemente lavoro motore (trattore agricolo).
MACCHINA (COMPOSTA) OPERATRICE: quella che trasforma lavoro
motore in lavoro utile ed è dotata di specifici organi operatori:
FISSE: pompe, ventilatori ...
- trainate
MOBILI: aratri, scavapatate, seminatrici ... - semiportate
- portate
SEMOVENTI: mietitrebbie, falciatrinciacaricatrici (FTC) ...
{
1)
MACCHINA (D.Lgs. 17/2010)
insieme equipaggiato o destinato ad essere equipaggiato di un sistema di azionamento
diverso dalla forza umana o animale diretta, composto di parti o di componenti, di cui almeno
uno mobile, collegati tra loro solidamente per un'applicazione ben determinata;
2)
insieme di cui al numero 1), al quale mancano solamente elementi di collegamento al sito di
impiego o di allacciamento alle fonti di energia e di movimento;
3)
insieme di cui ai numeri 1) e 2), pronto per essere installato e che può funzionare solo dopo
essere stato montato su un mezzo di trasporto o installato in un edificio o in una costruzione;
4)
insiemi di macchine, di cui ai numeri 1), 2) e 3), o di quasi-macchine, di cui alla lettera g - )
«quasi-macchine»: insiemi che costituiscono quasi una macchina, ma che, da soli, non sono
in grado di garantire un'applicazione ben determinata; un sistema di azionamento è una
quasi macchina; le quasi-macchine sono unicamente destinate ad essere incorporate o
assemblate ad altre macchine o ad altre quasi-macchine o apparecchi per costituire una
macchina disciplinata dalla presente decreto;), che per raggiungere uno stesso risultato sono
disposti e comandati in modo da avere un funzionamento solidale;
5)
insieme di parti o di componenti, di cui almeno uno mobile, collegati tra loro solidalmente e
destinati al sollevamento di pesi e la cui unica fonte di energia è la forza umana diretta
MACCHINA SEMPLICE: PIANO INCLINATO
{
Sollevare un peso mg ad una altezza h: peso troppo elevato: come diminuire la
forza richiesta?
Attr. di rotolamento
Piano inclinato + attrito di rotolamento (ruota)
Fm > fv mg cosα + mg senα =
= mg (cosα fv + senα)
Es.: per α = 20°:
Fm = (0,0188 + 0,342) mg =
= 0,36 mg < mg
Lm > (fv mg cosα + mg senα) (h/senα) = fv mg cosα/senα h + mgh =
= mgh (1 + fv/tgα)
Es.: per α = 20°: Lm = 1,055 mgh > mgh
MACCHINA SEMPLICE: PARANCO
O TAGLIA
RESISTENZE PASSIVE
RESISTENZA DI RIGIDEZZA DEGLI ORGANI FLESSIBILI
(cinghie, catene, funi, nastri…) a causa della loro non perfetta elasticità (flessibilità)
RESISTENZA DI ATTRITO RADENTE
nel caso di corpi che strisciano lungo una superficie di contatto e dovuta alla
scabrezza e alle forze di adesione lungo la superficie di contatto
RESISTENZA DI ROTOLAMENTO (o ATTRITO VOLVENTE)
nel caso di un corpo che rotola su una superficie e dovuta alle deformazioni non
elastiche dei corpi in contatto e alle asperità (urti) presenti
RESISTENZA o ATTRITO DEL MEZZO
nel caso dei corpi che si muovono immersi in un fluido (“resistenza aerodinamica”
nel caso dell’aria)
RESISTENZA DI ATTRITO INTERNO DI UN FLUIDO IN MOVIMENTO
resistenza allo scorrimento di un fluido dovuta alla viscosità (lubrificazione)
RESISTENZA DI RIGIDEZZA DEGLI ORGANI FLESSIBILI
Non perfetta elasticità di catene, cinghie, funi, quando sono
avvolte intorno a pulegge (carrucole, tamburi) o ruote dentate.
Per funi, cinghie:
cr = c1(d2/D)
c1 = coefficiente sperimentale (dimensionale)
d = diametro o spessore del flessibile
D = diametro puleggia = 2 r
cr tende a 0 per d2 << D
Per catene:
Organi perfettamente elastici:
Q(r+b) = P1(r+b)
Q = P1
Organi anelastici:
P2 = [(r+b)/(r-b1)]Q = cr Q
P2 > Q
cr coefficiente (adimensionale) > 1
Prescrizione di legge per funi metalliche:
cr = c2(d/D)
d = diametro elemento costituente la maglia
c2 = coeff. adimensionale sperimentale pari a 0,2 per
catene lubrificate e a 0,3 per catene asciutte
D > 25 d
e
D > 300 φ fili costituenti la fune
RESISTENZA DI ATTRITO RADENTE
CAUSE: scabrezza delle superfici e forze di adesione.
Se il corpo si muove su una superficie a velocità
costante (nessuna accelerazione e nessuna forza
di inerzia –ma) occorre applicare una forza T:
esiste allora una forza di attrito al contatto pari ad
A. Per l’equilibrio rispetto alla direzione x:
T+A=0
T–A=0
Sperimentalmente risulta: A = fa Fn
scalarmente, proiettando su x:
T=A
con Fn = forza che agisce normalmente alla direzione di moto tra le due superfici
in contatto;
fd = coefficiente di attrito “dinamico” (o “cinematico” o “radente”) (adimensionale)
• fd dipende fortemente dallo stato e natura delle superfici in contatto
• fd è indipendente, entro certi limiti, dalla pressione di contatto (p = Fn/S) e
dalla velocità
RESISTENZA DI ATTRITO RADENTE: coefficiente di primo distacco
Se il corpo è inizialmente fermo, occorre applicare una forza T’>T per metterlo in moto
T’ = fs Fn
fs > fd
F senϕ = fs F cosϕ
fs = senϕ / cosϕ = tgϕ
ESPERIENZA DI GALILEI:
piano inclinato –> il corpo rimane fermo finché non si raggiunge una certa
inclinazione (ϕ) del piano inclinato.
fs è il coefficiente di “attrito statico” o di “primo distacco”.
CUSCINETTO DI STRISCIAMENTO: 1 = cuscinetto o boccola o mozzo (fisso)
2 = perno (mobile)
r = raggio del perno
ρ = r senϕ = raggio di attrito
Mp = momento di attrito
Rt
Mp = Rt r = tgϕ Ri r = senϕ r (Ri / cosϕ) = R ρ
La reazione R che agisce sul perno è
sempre tangente al cerchio di attrito.
COEFFICIENTI DI ATTRITO STATICO E DINAMICO
Materiali a contatto
Stato delle superfici
fs
fd
0,30
0,15 ÷ 0,20
-
0,03
Secco
0,8 ÷ 0,9
0,75
Bagnato
0,5 ÷ 0,7
0,45 ÷ 0,60
Secca
0,68
0,65
Bagnata
0,55
0,40 ÷ 0,50
Pneumatico su neve
Pressata
0,20
0,15
Pneumatico su ghiaccio
-
0,10
0,07
Secche
Metallo su metallo
Pneumatico su asfalto
Pneumatico su terra battuta
Levigate e lubrificate
RESISTENZA DI ROTOLAMENTO
CAUSE: deformazioni al contatto e asperità presenti.
Per mantenere in rotolamento una ruota di raggio r a
velocità costante v e caricata da una forza G
centrata, si deve applicare una forza F nella
direzione e nel verso di avanzamento.
Per l’equilibrio dinamico (in assenza di accelerazioni)
la risultante R applicata alla ruota deve passare per il
centro della ruota (stesso punto di applicazione di G
e F) e devono valere le relazioni: G = Rn ; F = Ro
e, per l’equilibrio dei momenti rispetto a O (centro
della ruota):
Rn u = Ro r -> Ro = F = (u / r)Rn = fv G
con fv coefficiente di attrito di rotolamento = u / r
Ro si può interpretare come una resistenza di rotolamento (che si oppone al moto)
Per l’attrito di rotolamento la reazione del terreno sulla ruota è spostata in avanti di u e
passa per il centro della ruota (deformazioni mutue ruota e terreno con pressioni non
simmetriche al contatto).
Quanto grande u? -> per fv = 0,02 -> u = 2% del raggio della ruota
RESISTENZA DI ROTOLAMENTO
L’attrito di rotolamento dipende anche dalla
deformabilità del terreno (es.: sabbia…)
… dagli urti che avvengono, lungo il percorso, con le
asperità presenti.
aumenta al diminuire di p):
fv = c0 + c1 v2
In questo caso le perdite per urto sono proporzionali
al quadrato della velocità.
Per rotolamento di pneumatici su strade asfaltate (fv
c0 = 0,01 ÷ 0,02
c1 = (6 ÷ 8) 10-6 s2/m2
v in m/s
COEFFICIENTI DI RESISTENZA AL ROTOLAMENTO (fv)
Tipo di pneumatico
Asfalto Calcestruzzo
Suolo duro
medio
Sabbia
Autoveicolo
0,015
0,08
0,30
Autocarro
0,012
0,06
0,25
Trattore agricolo
0,02
0,04
0,20
Trattore a cingoli
-
0,04 ÷ 0,07
0,08 ÷ 0,13
Questi coefficienti sono
assimilabili a quelli globali di
“resistenza
all’avanzamento” (o di
“autodislocamento”)
dell’intero veicolo.
Prodotto vettoriale dei vettori A e B: vettore prodotto C di modulo C = A B senθ,
direzione ortogonale al piano A-B; verso della terna levogira: A come x, B come y,
C come z
z
x
y
Il moto di rototraslazione di una
ruota è somma di due moti
componenti:
- moto di traslazione con velocità di
avanzamento va uguale a vc per
tutti i punti della ruota (vc = velocità
del centro della ruota)
- moto di rotazione intorno al centro
della ruota con velocità angolare
ω=va/r (r = raggio della ruota)
Risulta una velocità nulla al punto di contatto (O): centro di istantanea rotazione.
Risulta ancora una velocità 2va in sommità della ruota.
PROBLEMI LEGATI AL MOTO DI ROTOTRASLAZIONE
Ruota deformabile:
pneumatico
Slittamento delle ruote
motrici
PNEUMATICO
(Dunlop, 1888: veterinario inglese)
camera d’aria (assente nei
tubeless)
copertura (o copertone)
– carcassa (o pacco tele)
(diagonale o radiale)
– battistrada
FUNZIONI:
sopportare il peso del
veicolo
assorbire gli urti per
l’asperità del percorso
fornire aderenza in trazione
e frenata
fornire stabilità direzionale al
veicolo e adeguato controllo
in sterzatura
PNEUMATICI: NOMENCLATURA
COPERTURE
E = larghezza o ingombro trasversale massimo
del pneumatico o corda
R = raggio senza carico
R1 = raggio sotto carico
h = altezza di sezione
h/E = rapporto nominale d’aspetto in %
(100: standard; 80: larghi; 70: extralarghi; 65: min.
trattori; 35: Ferrari F40, Lamborghini Diablo)
Φ = diametro di calettamento
CERCHI
F = larghezza interna
H = altezza dell’agganciatura
Φ = diametro di calettamento
R1 < r0 < R
r0: raggio di rotolamento: dipende
dalla pressione e dal carico normale
agente (quello sui cataloghi a pressione
e carico nominale)
c.d.r.: circonf. di rotolamento (dinamica)
PNEUMATICI: DIAGONALI E RADIALI
A: tradizionale o diagonale
B: radiale
VANTAGGI DEL RADIALE:
1. Ottima aderenza: il pneumatico ruota (avanza) come un cingolo, quindi migliore trattamento del
terreno, migliore aderenza e minore slittamento
2. Migliore ripartizione della pressione interna che determina una minore compattazione del terreno
3. Riduzione dei tempi di lavoro, produttività in aumento
4. Economia di carburante in ragione della ridotta resistenza all’avanzamento
5. Aumento del rendimento chilometrico (durata anche doppia)
6. Comfort di marcia e maggiore salvaguardia degli organi meccanici per l’elevata flessibilità della
carcassa
7. Minore potenza dissipata nel rotolamento (fino a -40% rispetto al diagonale)
PNEUMATICI: MARCATURA
16.9/65 R 38 BIB’X
M
18
140 A 8
137
B
RADIAL
16.9
Larghezza di sezione espressa in pollici (o mm)
65
Rapporto nominale d’aspetto (h/E in %) (se manca si sottintende 80)
R
Struttura radiale (se manca: diagonale)
38
diametro di calettamento in pollici (o mm)
BIB’X
Identificazione del pneumatico (proprio di Michelin: X marchio dep.)
M
18
Tipo di scultura
140
Indice della capacità di carico: 2500 kg
A8
Simbolo categoria di velocità: 40 km/h
137
Indice della capacità di carico (2300 kg) per velocità di 50 km/h (B)
RADIAL Indicazione in chiaro della struttura
PNEUMATICI
PRESSIONE SUL TERRENO = PRESSIONE DI GONFIAGGIO
(Vero se il pneumatico fosse costituito da sola camera d’aria: organo completamente flessibile)
TIPI DI BATTISTRADA: - per ruote motrici (a centro chiuso; a centro aperto)
- per ruote direttrici
SLITTAMENTO
È difficile realizzare un moto di pura rototraslazione. Una ruota trainata avanza
rotolando e strisciando (lo strisciamento non è desiderato).
Una ruota motrice che scarica a terra una forza motrice, in generale avanza
rotolando e slittando (si ha puro slittamento quando la ruota motrice ruota sul posto
senza avanzare).
Lo slittamento si risolve in una diminuzione della velocità teorica (vt) di
avanzamento.
Se la ruota è dotata di una velocità angolare ω la velocità teorica di avanzamento
è:
vt = ω r
(r = raggio della ruota)
Se la velocità effettiva di avanzamento è v, si definisce slittamento:
vt - v
v
=
1
s=
vt
vt
In percento:
v
s% = (1 -
vt
) ∗ 100
Risulta complicato misurare lo slittamento mediante le velocità v e vt.
Le norme di omologazione dei trattori prescrivono la misura, su una base di
lunghezza L (> 100 m), del numero di giri delle ruote motrici sotto carico (n) e a
vuoto (n0) e lo slittamento è dato da:
n - n0
s =
n
n0 Rendimento di
ηs = 1 - s =
n slittamento
Sotto carico: con traino del carro freno che realizza varie forze di traino.
A vuoto: senza traino.
Le prove per i trattori a ruote avvengono su pista
di calcestruzzo o asfalto (tarmacadam) e lo
slittamento a vuoto si può ritenere trascurabile.
Per i trattori a cingoli tutto analogo: tutto riferito
alla ruota motrice del cingolo
(pista di prova un terreno inerbito piano, secco,
orizzontale, falciato o brucato, o su terreno di
buona aderenza).
Nei trattori 4RM non meccanicamente bloccate o bloccabili insieme, gli slittamenti
delle singole ruote possono essere diversi: le norme OCSE prescrivono le singole
misure e la segnalazione se i valori differiscono di oltre il 5%.
Nel caso di trattori 4RM è conveniente avere gli stessi slittamenti per l’assale
anteriore e posteriore: altrimenti si avrebbero sollecitazioni nelle trasmissioni e
strisciamenti (un assale frena rispetto all’altro).
In trattori 4RM con ruote “isodiametriche” è allora importante che la velocità
angolare delle ruote anteriori sia uguale a quella delle ruote posteriori (velocità di
avanzamento delle anteriori uguale a quella delle posteriori).
È però essenziale che il raggio di rotolamento delle ruote sia uguale, condizione
non facile da soddisfare:
- non prevedibilità di trasferimento dei carichi in lavoro;
- pressioni di gonfiaggio diverse;
- diversa usura del battistrada.
Nel caso di trattori 4RM con diametro delle ruote anteriori diverso da quello delle
posteriori è difficile dare indicazioni. Le case costruttrici “anticipano” (più veloci) le
anteriori per fare in modo che queste non siano di freno alle posteriori.
PNEUMATICI
Le pressioni di gonfiaggio di un pneumatico agricolo variano tra 50 e 300 kPa (0,5
÷ 3 kgp/cm2). Se il pneumatico fosse un organo completamente flessibile la
pressione di scarico a terra sarebbe pari alla pressione di gonfiaggio: all’aumentare
del carico verticale agente aumenterebbe l’area di impronta, ma non la pressione di
scarico al suolo.
Questo non è vero a causa della rigidità del copertone, ed è tanto meno vero
quanto sono più elevate le pressioni di gonfiaggio (oltre 2,5 ÷ 3 kgp/cm2 il
pneumatico si comporta come un organo rigido).
Si ha, quindi, la convenienza ad avere pressioni di gonfiaggio basse per i
pneumatici agricoli, in modo da avere basse pressioni al suolo perciò un contenuto
costipamento del terreno.
Pressione esercitata sul terreno da uomo fermo calzato: circa 0,2 kgp/cm2 = 20
kPa.
Se l’uomo cammina: 0,2 ÷ 1,5 kgp/cm2 = 20 ÷ 150 kPa.
Una donna con tacchi a spillo determinerebbe delle pressioni sul terreno
estremamente più elevate.
LAVORO: L = F s = F s cosθ (prodotto scalare della forza (F) e del vettore
spostamento considerato (s)). In termini semplici: il prodotto di una forza per lo
spostamento del suo punto di applicazione misurato nella direzione e verso
della forza.
Grandezza scalare
Unità di misura di base: Nm = J
(joule)
POTENZA: P = L / t = (F s cosθ) / t = F v
(v = velocità misurata nella
direzione e verso della forza)
Unità di misura di base: J/s = W
(watt)
Vecchie unità di misura: CV = 75 kgpm/s = 736 W
+ 1,4%
HP = 550 lbpft/s = 746 W
Unità di misura consentita per il lavoro, a partire dal watt:
kWh = 3.600 x 103 J = 3,6 MJ
POTENZA MEDIA GIORNALIERA DI ALCUNI MOTORI ANIMATI E NO
(Carena, 1947)
F media di
trazione
(kgp)
V media
(m/s)
P media
(W)
-
-
70-75
1
CAVALLO
100
0,90
883
12
BUE
120
0,65
765
10
MULO
65
0,90
574
8
ASINO
40
0,70
274
4
-
-
574.000
(574 kW)
7.757
UOMO
Caterpillar
D 11 N
Valori
indice
(uomo vapore)
MOTI DI ROTAZIONE
MOMENTO DI UNA FORZA rispetto a un punto (o polo) O:
M = OP x F
F
Grandezza vettoriale
Modulo = OP F senθ =
=bF
(b = braccio della forza)
O
θ
P
b=OP senθ
Direzione: ortogonale al piano OP-F
Verso: quello da cui si vede avvenire la rotazione intorno ad O in senso antiorario
COPPIA: due forze uguali, con verso
contrario e direzioni parallele
Il modulo non varia al variare del polo
considerato (b = costante)
Il momento di una forza misura l’effetto della stessa rispetto ad un asse di rotazione.
PRINCIPIO DELLA LEVA:
Fm = Fr a / b
La forza motrice Fm sarà tanto minore quanto maggiore è il braccio b.
LAVORO IN UN MOTO ROTATORIO:
L=Mα
Prodotto scalare tra vettore momento e vettore spostamento angolare
L=+Mα
Se lo spostamento angolare è misurato nel piano ortogonale ad M
POTENZA IN UN MOTO ROTATORIO:
P = L / t = (M α) / t = M ω
(ω = velocità angolare misurata nella stessa direzione e
verso del momento)
Per un albero motore che ruota a 2.500 giri/minuto erogando una coppia (momento) di 300
Nm:
P = 300 x (2.500 x 2π) / 60 = 78.540 W = 78,54 kW
In un moto rotatorio l’inerzia di un corpo è misurata dal MOMENTO D’INERZIA (I)
rispetto all’asse di rotazione.
M = Ia ω
(Ia = momento d’inerzia rispetto all’asse;
ω = accelerazione angolare)
2
2
Ia = ∑i mri i = m∫ r dm
Assi principali (o “liberi” o “spontanei”) di rotazione: baricentrici e quelli rispetto ai quali si
annulla la risultante e il momento risultante delle forze centrifughe (es.: equilibratura delle
ruote).
ENERGIA MECCANICA: la capacità di un sistema a compiere lavoro.
Ep = m g h
energia potenziale
Ec = 0,5 m v2
energia cinetica di traslazione
Ec = 0,5 I ω2
energia cinetica di rotazione
ASSI PRINCIPALI (o liberi o spontanei) DI ROTAZIONE
Baricentrici e quelli rispetto ai quali si annulla la risultante ed il momento risultante
delle forze centrifughe (m ω2 r)
EQUILIBRATURA DINAMICA DELLE RUOTE
(m = massa non bilanciata)
La ruota tende ad oscillare intorno ad O [(A) e (B)].
Se si bilancia con un’altra massa m, ma non sullo stesso piano, si genera una coppia che
tende ugualmente a far oscillare la ruota [(C) e (D)].
STATICA
z
y
Studio dell’equilibrio dei corpi
x
Nello spazio:
Σ Fe = 0
no traslazioni o accelerazioni
Σ Me = 0
no rotazioni (neanche intorno ad un asse
passante per il corpo)
L’indice “e” sta per “esterne” (solo forze esterne).
Nel piano xy le condizioni precedenti equivalgono alle tre condizioni scalari:
Σ Fx = 0
no traslazioni o accelerazioni lungo x
no traslazioni o accelerazioni lungo y
Σ Fy = 0
ΣM=0
(rispetto ad un qualsiasi punto del piano) no rotazioni rispetto a un
qualsiasi asse perpendicolare al piano xy (parallelo a z) o
accelerazione angolare rispetto a z (ωz)
CASI PARTICOLARI DI SISTEMI PIANI DI FORZE:
- due forze sono equilibrate se costituiscono una coppia di braccio nullo
- tre forze sono equilibrate se concorrono tutte in uno stesso punto e la risultante di due qualsiasi
costituisce una coppia di braccio nullo con la terza
- quattro forze sono equilibrate se la risultante di due qualsiasi costituisce una coppia di braccio nullo
con la risultante delle altre due
RESISTENZE PASSIVE
Sono tutte quelle forze che si oppongono al moto determinando una perdita di
energia meccanica in calore.
Sembrano avere connotati solo negativi ma sono essenziali affinché il moto stesso
possa avvenire e avvenire in sicurezza:
• messa in marcia di un veicolo (perché c’è sufficiente “aderenza” tra ruota e
terreno;
• arresto di un veicolo perché c’è “attrito” ai freni e “aderenza” tra ruota e
terreno).
Lo stesso fuoco nel paleolitico e neolitico era gestito per “attrito”.
La stessa vela ha reso possibile la navigazione per la “resistenza aerodinamica” al
vento.
RUOTA MOTRICE TRAINANTE
1
2
=0
{ ΣF
-T - R + F = 0
=0
{ ΣF
-F + R = 0
x
t
y
n
3
Da 1
Da 2
Da 3
t
{
Ft = T + Rt
Fn = Rn
Mm = Ft r = (T + Rt) r = Tr + Rt r
Fm = Mm / r = Ft = T + Rt
n
ΣM = 0
R passa per O
Ft r – Mm = 0
…e, dividendo tutto per r…:
Fm = forza motrice disponibile alla periferia della ruota e di verso contrario a Ft
Fm è la forza che la ruota esercita sul terreno;
Ft è la forza di reazione che il terreno esercita sulla ruota ed è quella che agisce nella
direzione e verso dell’avanzamento: l’effettiva forza motrice per la ruota.
ADERENZA
Sotto quali condizioni il terreno può applicare alla ruota la forza Ft (= -Fm)?
Ft ≤ fs Fn = ca Fa
ca = coefficiente di aderenza (assimilabile in prima approssimazione a fs)
Fa = peso aderente: quella parte del peso del veicolo che si scarica sulle ruote motrici
Ft = fs Fn = ca Fa -> Forza limite di aderenza
ca
ADERENZA
Ft = ca Fa
Valido anche
per l’intero veicolo
Fa
{
- stato e natura delle superfici in contatto
(pneumatico radiale, cingolo)
{
- peso aderente (zavorratura; doppia traz.: 2 RM -> 4 RM):
- slittamento (cresce, entro certi limiti, al crescere di s)
- pressione gonfiaggio (cresce al decrescere di p)
l’aumento di Fa con le zavorre aumenta, però, la perdita per
autodislocamento
È l’aderenza (Ft) che limita il “tiro” di un trattore, non la sua potenza.
Una teoria elementare dell’aderenza deve spiegare la
dipendenza di ca dallo slittamento (s)
ADERENZA
Pneumatico su mezzo rigido (es.: asfalto…)
v
r0 = raggio di rotolamento sotto l’azione
del carico verticale nominale e della
pressione di gonfiaggio nominale
m
r 0’ < r 0
r0’ = raggio di rotolamento quando è
applicato un momento motore
r0’ è tanto minore quanto maggiore Mm
e quindi T
Fase elastica
s = (vt – v) / vt = (ω r0 – ω r0’) / ω r0 = 1 – (r0’ / r0)
Fase con slittamenti effettivi ruota-strada
ADERENZA
Pneumatico su mezzo deformabile (es.: terreno agrario…)
Occorre considerare e introdurre le caratteristiche di
resistenza del terreno.
(Analogia: τ come ca; spostamento come “slittamento”)
“Scatola di Casagrande” per la determinazione dei
parametri di resistenza del terreno.
Applico una forza T per rompere a taglio il provino. La
forza T a rottura è funzione di Fn e per vari valori di T e
Fn posso ricavare una retta di resistenza: τr = c + σ tgϕ
Un terreno è, in generale, un materiale
coesivo (c = coesione) e attritivo (ϕ =
attrito interno).
Argille in condizioni non drenate: solo
coesive (cu)
ADERENZA
La forza limite di aderenza è data da:
Ft = ca Fa = S tr = S (c + σ tgϕ)
ca Fa = c S + σ S tgϕ = c S + Fn tgϕ
ca = c / p + tgϕ *
Fa = Fn
p = Fa / S (pressione al suolo)
S = superficie di appoggio delle ruote motrici
(o dei cingoli)
In un terreno coesivo e attritivo ca dipende essenzialmente da tgϕ (tgϕ >> c/p)
In un’argilla in condizioni non drenate (ϕ ≅ 0) ca dipende da c/p: basse pressioni al
suolo sono essenziali.
* Il valore di ca che proviene dalla
formula è approssimato per eccesso:
quando il terreno “si rompe” sotto la
ruota (o il cingolo) non “tutto” ha
raggiunto le condizioni limite di rottura.
CARATTERISTICHE c E ϕ PER VARI TERRENI
Terreno
c [kPa]
cr [kPa]
ϕ
ϕr
Sabbia asciutta
1,07
-
28°
-
Sabbia limosa
1,72
1,38
29° 38°
Argilla drenata
68,95
20,69
34°
Neve
1,03
0,62
20° 23°
35÷400
-
Argille limose non drenate (cu)
-
6°
-
RESISTENZA AERODINAMICA
Ra = ρ Cx Af v2 / 2
Ra = resistenza aerodinamica
ρ = massa volumica dell’aria (≅ 1,2 kg/m2)
Af = area frontale del veicolo (area proiettata su una superficie ortogonale al moto)
v = velocità
Cx = coefficiente di resistenza aerodinamica
(adimensionale)
In un trattore a v = 11,11 m/s (40 km/h), con Af = 4 m2 e
Cx = 1,1, con ρ = 1,2 kg/m3 si ha:
Ra = 1,2 x 1,1 x 4 x 11,112 / 2 = 326 N
Potenza dissipata = P = 11,11 x 326 = 3.622 W ≅ 3,6 kW
Se il trattore ha una potenza di 50 kW, la potenza dissipata
è pari al 7%.
Tipo di veicolo
Autovettura
Cx
0,3 ÷ 0,6
“
decapottabile
0,4 ÷ 0,65
“
da corsa
0,25 ÷ 0,3
Autobus
0,6 ÷ 0,7
Autocarro
0,8 ÷ 1,0
Trattore - Roulotte
0,8 ÷ 1,3
Motocicletta e motociclista
1,8
ESEMPIO DI CALCOLO DI PERDITE DI AUTODISLOCAMENTO
PER UN TRATTORE
Trattore a ruote da 50 kW e massa 3.000 kg
1) Se si muove su asfalto con fv = 0,02 a velocità di 11,11 m/s (40 km/h):
Resistenza all’avanzamento: Ra = fv m g
Ra = 0,02 x 3.000 x 9,81 ≅ 589 N
Potenza dissipata: P = Ra v
P = 589 x 11,11 = 6.544 W ≅ 6,5 kW
in percento della sua potenza: (6,5 / 50) x 100 = 13%
2) Se si muove su sabbia con fv = 0,20 a velocità di 2,78 m/s (10 km/h):
Ra = 0,2 x 3.000 x 9,81 = 5.886 N
P = 5.866 x 2,78 = 16.363 W ≅ 16,4 kW
in percento della sua potenza: (16,4 / 50) x 100 = 33%
ESEMPIO DI CALCOLO DELLA FORZA LIMITE DI ADERENZA E DI
TRAZIONE (TIRO)
Trattore a ruote 4 RM da 50 kW e massa 3.000 kg
1)Se si muove su asfalto con ca = 0,80
Forza limite di aderenza: Ft = ca Fa = ca Fn = 0,8 x 3.000 x 9,81 = 23.544 N≅23,5 kN
peso totale trattore (4 RM)
Calcolare il tiro massimo T con un coeff. di autodislocamento (fv o ka) di 0,02:
T = Ft – fv Fn = 23.544 – 0,02 x 3.000 x 9,81 = 23.544 – 589 = 22.955 N ≅ 23 kN
Coefficiente di trazione:
CT = T / Fn = 22.955 / (3.000 x 9,81) = 78%
Se il trattore ha una velocità di 5 km/h (1,39 m/s) quanto vale la potenza sviluppata
(utile) al gancio?
Pu = T v = 23 kN x 1,39 m/s ≅ 32 kW
Quanto vale il rendimento al gancio? ηg = Pu / Pmax = 32 / 50 = 64%
STERZATURA CINEMATICA DI UN
VEICOLO A RUOTE DIRETTRICI ANTERIORI
(α al massimo = 50°)
p = passo (distanza tra
gli assi del veicolo)
c = carreggiata
Affinché le ruote in curva ruotino senza strisciare
devono avere uno stesso centro di rotazione.
Deve risultare:
Po sul prolungamento dell’assale delle ruote (fisse
sull’assale);
Angoli di sterzo α e β delle ruote direttrici diversi
Raggio minimo di sterzata (PoC) del veicolo pari a:
PoC = r = p / senβ
(β = 35°-> r = 1,7 p)
r tanto minore quanto minore p e maggiore α
(α ≈ 50°) (per α ≈ 50°-> β ≈ 30°÷ 40°)
STERZATURA CINEMATICA DI UN
VEICOLO A RUOTE DIRETTRICI ANTERIORI
a = distanza tra i perni a
snodo ~ carreggiata o
scartamento delle ruote
anteriori
cotα = PoE / ED
cotβ = PoF / FC
FC = ED = p
cotβ – cotα = (PoF – PoE) / p = a / p
condizione di sterzatura cinematica esatta
affinché tutte le ruote abbiano uno stesso
centro di volta.
Difficile da realizzare; ci si accontenta di
soluzioni approssimate:
quadrilatero di sterzo a bracci (A’C e B’D)
paralleli (buona fino ad angoli di sterzo di
circa 10°) (Lankesperger 1817; Ackermann)
quadrilatero di sterzo trapezio con bracci
concorrenti sull’asse posteriore o poco
davanti (buona fino a circa 20°)
(Janteaud 1878)
STERZATURA DEI VEICOLI A RUOTE
a) veicolo
a volta semplice
b) veicolo a 4 ruote direttrici
con sterzatura in croce
(volta corretta)
c) veicolo a 4 ruote direttrici
con sterzatura in fase (a
granchio)
d) veicolo a sterzatura
articolata (telaio non rigido
ma con snodo centrale)
(volta corretta)
Nel caso a) le ruote interne (e le esterne) percorrono traiettorie in curva diverse (volta semplice). Nei casi b)
e d) le ruote interne (e le esterne) percorrono la stessa traiettoria (volta corretta).
Trattori (non articolati): ruote sterzanti anteriori. Mietitrebbiatrici: ruote sterzanti posteriori.
Nel caso a) con ruote anteriori sterzanti la
manovrabilità del veicolo è migliore in
retromarcia (raggi di volta ruote posteriori minori
rispetto anteriori).
STERZATURA DEI VEICOLI A RUOTE:
IL DIFFERENZIALE
VEICOLI A VOLTA SEMPLICE
In curva le ruote motrici posteriori (e nei
trattori 4RM anche le anteriori)
percorrono traiettorie diverse: devono
avere velocità di avanzamento diverse
esigenza del differenziale (posteriore
e, nei 4RM anche anteriore)
In curva comunque l’assale posteriore
percorre una traiettoria diversa da
quello anteriore: ad alta
velocità si ha (nei 4RM)
la necessità anche di un
differenziale centrale (A)
4RM ≡ 4WD
4 ruote motrici ≡ 4 wheels driven
FUNZIONAMENTO IN TRANSITORIO E
A REGIME DI UNA MACCHINA
Il funzionamento di una macchina presenta:
1.
Una fase di avviamento: parte dell’energia in ingresso serve per fornire
energia cinetica agli organi; le forze motrici devono inizialmente accelerare
gli organi meccanici “vincendo” le forze di inerzia (-ma); Ei>Eu+Ed
∆Ec=Ei-Eu-Ed
2.
Una fase a regime: tutti gli organi hanno acquisito un’energia cinetica
(media) costante; le prestazioni della macchina rimangono costanti; le forze
motrici equilibrano le sole forze resistenti (resistenze utili + resistenze
passive); Ei=Eu+Ed
3.
Una fase di arresto: viene dissipata in calore tutta l’energia cinetica della
macchina che si pone in stato di quiete; Ei<Eu+Ed ∆Ec=Eu+Ed-Ei
Fasi 1 e 3: transitori o funzionamento in transitorio
Fase 2: a regime o funzionamento a regime
A noi interessano, quasi sempre, solo le fasi a regime.
Regime assoluto o periodico: quando forze, velocità… variano nel tempo ma
assumono gli stessi valori dopo intervalli di tempo costanti (periodo)
Ei = energ. o lavoro in ingresso
Eu = energ. o lavoro utile
Ed = energ. o lavoro passivo
Ec = energ. cinetica
DEFINIZIONE DI RENDIMENTO A REGIME
Ei o Pi: energia o potenza assorbita in ingresso
Eu o Pu: energia o potenza utile in uscita
Ed o Pd: energia o potenza dissipata (degradata)
in calore a bassa temperatura
Per il primo principio della termodinamica
(l’energia non si crea né si distrugge):
Ei = Eu + Ed o Pi = Pu + Pd
Rendimento η = Eu/Ei = (Ei-Ed)/Ei = 1-(Ed/Ei) o η = 1-(Pd/Pi)
1) una macchina che trasmette solo energia meccanica (per esempio: un cambio) ha
un rendimento teorico ideale (limite) di 1 (100%): basta annullare (lubrificazione
ideale) tutte le resistenze passive (Ed o Pd = 0)
2) una macchina termica (un motore che trasforma energia termica o calore in lavoro
meccanico utile) ha un rendimento teorico ideale minore di 1 e al limite pari a quello
del ciclo di Carnot associato alle temperature estreme del ciclo:
η= 1-(T2/T1); T2<T1 e η<1
(condizione matematica, ma non fisica, per η=1: T2=0 K e/o T1 = ∞ K )
RENDIMENTI DI MACCHINE COLLEGATE
IN SERIE
η = η1 × η2 =
Eu
Eu'
Eu'
×
=
Ei
Ei' (= Eu)
Ei
(Prodotto dei singoli rendimenti)
IN PARALLELO
Ei = Ei' + Ei''
Eu = Eu' + Eu''
Eu'
Eu''
η1 =
; η2 =
Ei'
Ei''
Eu
η Ei' + η2 Ei''
η =
= 1
Ei
Ei' + Ei''
(Media pesata dei singoli rendimenti,
con pesi le singole energie in ingresso)
RENDIMENTI PER UN TRATTORE IN “TRAZIONE”
Rendimento di trasmissione
ηtr = (Pm – Wt)/Pm
Rendimento di autodislocamento
ηd = (Pm – Wt – Wd)/(Pm – Wt)
Rendimento di slittamento
ηs = (Pm – Wt – Wd – Ws)/(Pm – Wt - Wd)
= 1 – s = (n – (n – n0))/n
s = (n – n0)/n
n = giri ruote motr. a carico
n0 = giri ruote motr. a vuoto
Rendimento globale al gancio
ηg = Pu / Pm = ηtr ηd ηs = 40 ÷ 70%
CLASSIFICAZIONE DEI TRATTORI
TRATTORE
Gommato
Telaio rigido
Ruote sterzanti
Ruote sterz. anteriori
Cingolato
Telaio articolato
Sterzatura per slittamento
(come i cingolati)
4 ruote sterzanti
Sterzatura per strisciamento
Con freni e frizioni di sterzo
(soluzione classica)
Differenziale controllato
A ruotismi epicicloidali
Ruote sterz. posteriori
Spesso le parole “slittamento” e “strisciamento” sono impiegate nei testi con lo stesso significato
(“skid” in inglese)
Ripartizione statica delle masse nei diversi tipi di trattori
2RM
DT
4RM
50% ant.
50% post.
CINGOLATO
Forza peso ripartita
tra:
RT=ruota
tendicingolo
RM=ruota
motrice
rac=rulli
appoggio
cingolo
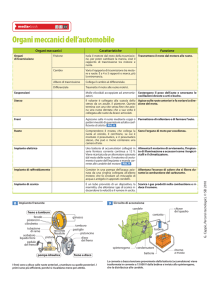
TRATTORE: PARTI COSTITUENTI
7
6
1.
2.
3.
4.
5.
6.
1
2
5
4
3
7.
Supporto assale
anteriore
Motore
Scatola frizione e
cambio di velocità
Scatola della
trasmissione finale
Flangia attacco scatole
riduttori laterali
Scatola della presa di
potenza
Sollevatore idraulico
MOTORI: CLASSIFICAZIONE
Termici
Esotermici
(o a combust. esterna)
Endotermici
(o a combust. interna)
Volumetrici*
Alternativi a vapore
(locomotiva...)
Alternativi a aria
(Stirling)
Continui
Turbina a vapore
Volumetrici*
Alternativi
Accensione comandata
A carburatore
A iniezione
Continui
Rotativi
(Wankel)
Accensione spontanea
A gas
*se la “camera” o “spazio” del motore varia di volume
durante il ciclo
Diesel
Semi-Diesel
(Testa calda)
Turbina a gas
Reattore
SVILUPPO STORICO
Età greco-romana: mulino ad acqua, carrucola, paranco (o taglia), argano, leva, vite di Archimede,
pompa a stantuffo, turbina a reaz. di Erone, ruota dentata e ingranaggi.
Età medioevale: mulino ad acqua (perfezionato), motori eolici, albero a gomiti
1629: Turbina ad azione (Branca)
1690: Macchina a vapore di Papin
1712: Macchina a vapore di Newcomen
1782: Macchina a vapore a doppio effetto di Watt (Watt: ruot. epicicloidale e regol. centrif.)
1800: Pila di Volta
1862: Ciclo a 4 tempi di Beau de Rochas
1905-’09: Buchi: turbocompressore
1867: Motore Otto
1914-’18: Sovralimentazione meccanica
(aereo con mot. asp. a 5500 m -> Pot. X 0,5)
1883: Turbina a vapore ad azione di De Laval
1919: Prima trattrice Fiat
1884: Turbina a vapore a reazione di Parson
1923: Fiat: macchina da gran prix a
1885: Motore elettrico a c.a. di G. Ferraris
sovralimentazione meccanica
1889: Pneumatico Dunlop
1928: Cambio sincronizzato (Cadillac)
1892: Trattrice Froelich (John Deere)
1938: Trasmissione automatica (giunto
1893: Ciclo Diesel (motore costruito nel 1897)
idraulico) (Crysler Fluid Drive)
1896: Auto Ford
1948: Convertitore di coppia/Giunto
1899: Auto Fiat
idraulico (Buick, GM)
1905: Fottinger: amplificatore di coppia (idraulico)
1959: Power Shift totale (trasmissione
automatica) (trattrice Ford 681 Select-OSpeed)
Miglioramento continuo dei materiali,
combustibili, lubrificanti
CARATTERISTICHE IDEALI DI UN MOTORE PER
AUTOVEICOLI INDUSTRIALI O PER TRAZIONE AGRICOLA
Economiche:
Basso costo di produzione, manutenzione, riparazione e di funzionamento
(anche basso costo combustibile)
Servizi di assistenza tecnica rapidi ed efficienti
Tecniche:
Elevato rendimento (bassi consumi specifici - g/kWh - a tutti i regimi e
carichi)
Elevata riserva di coppia (Cmax-CPmax)/CPmax
Elevata potenza per unità di cilindrata (kW/L cil.)
Elevata potenza per unità di massa (peso) (kW/t)
Minimo ingombro
Lunga durata o vita utile (>10.000 h)
Affidabilità (pochi “fuori servizio”) e facilità di riparazione
Semplicità, facilità e comfort di conduzione (guida)
Ridotte emissioni nocive (motore ecologico ?!?)
MOTORE
Motore Diesel
a 3 cilindri a valvole
in testa
(valvole “laterali”: architettura del motore più
vecchia. Attualmente motori con valvole “in
testa” comandate da aste e bilancieri)
MOTORE: IL CILINDRO
Le “canne” o “camicie cilindri” sono
sistemate nel “gruppo cilindri” ricavato
nel “basamento motore” (in ghisa).
Canne “in umido”: in contatto con
l’acqua di raffreddamento.
Canne “a secco”: non in contatto con
l’acqua di raffreddamento.
A: nessuna camicia;
B: canna entro il
“Testa cilindri” o “testata” in ghisa:
cilindro;
ospita gli iniettori, le valvole di
C: la canna è il
aspirazione e scarico e i relativi
cilindro.
bilancieri. Vi sono collegati i collettori di
aspirazione aria e di scarico gas.
Guarnizione di tenuta tra testata e
basamento.
Sistemazione della canna con pressa
MOTORE: IL PISTONE
(NO nei motori Diesel)
}
Nel “cielo” del pistone è ricavata la
“camera di combustione”
MOTORE: ALBERO MOTORE
Volano: corona dentata per motore elettrico di avviamento.
Ingranaggio per comando: distribuzione, pompa olio,
equilibratore a masse controrotanti.
Puleggia per: pompa acqua, ventilatore, generatore elettr.
In acciaio
stampato
È sostenuto dai “supporti di banco”.
I perni dell’albero motore sono induriti
superficialmente e levigati. Ruotano su
cuscinetti di strisciamento (“bronzine”)
“a guscio sottile” (2 mm) costituiti da un
guscio di acciaio ricoperto di una lega
antifrizione dello spessore di qualche
decimo di mm.
MOTORE: DISTRIBUZIONE E VALVOLE
Bilancieri
VALVOLE
Albero di
distribuzione
(a “camme”)
SEDI DELLE VALVOLE
CINGHIA DI DISTRIBUZIONE
TESTATA
MOTORE: DISTRIBUZIONE E VALVOLE
MOTORE: ALIMENTAZIONE E INIEZIONE
INIEZIONE DIRETTA
INIETTORE
1.Meno
dispersioni (maggior rendimento)
2.Più elevate pressioni di iniezione
(150÷250 kgf/cm2 15÷25 MPa)
3.Migliore partenza a freddo
4.Più difficoltà di miscelazione
aria/gasolio
5.La polverizzazione del getto di gasolio
deve essere più spinta (vedi punto 2)
6.φ cilindri opportuno per garantire la
polverizzazione (φ> 90 mm)
INIEZIONE INDIRETTA
A: pompa di alimentazione combustib.
1.Pressioni di iniezione più basse
B: filtro combustibile
(80÷120 kgf/cm2 8÷12 MPa): la camera
C: filtro combustibile di carta
aggiuntiva facilita la turbolenza e la
D: segnalatore intasamento filtro aria
miscelazione gasolio/aria
E: iniettori
2.Necessità di “candelette” per
F: filtro aria a secco
avviamento a freddo
P: pompa di iniezione
S: serbatoio combusibile
1 kgf/cm2 = 100 kPa
1. Recupero trafilamento
2. Disco di registrazione
3. Molla di pressione
4. Luce di ingresso
5. Filtro a barretta
6. Camera a pressione
7. Corpo iniettore
8. Polverizzatore ad ago e
foro/i
MOTORE: RAFFREDDAMENTO
Raffreddamento ad aria (ventilatore + alette di
raffreddamento aumento superficie scambio termico).
Raffreddamento ad acqua: circuito idraulico, pompa (P),
radiatore (R), vaso di espansione (S), termostato (T),
ventilatore (V), liquido non gelivo.
v
MOTORE: LUBRIFICAZIONE
Biella
Filtro
Albero a camme
Assi porta-bilancieri
comando valvole
Sezione di filtro olio
Valvola di by-pass
Albero motore
Coppa dell’olio
Pompa a ingranaggi
Uscita olio
Mezzo filtrante
Ingresso olio
TERMOLOGIA E TERMODINAMICA
• TEMPERATURA:
Grandezza scalare intensiva
Misura lo stato termico di un corpo
Unità di misura di base: K
(kelvin) (la frazione 1 / 273,16 della temperatura
termodinamica del “punto triplo” dell’acqua -Conf. Gen. Pesi e Misure 1967-).
Punto triplo preferito rispetto al (vecchio) punto di fusione, perché più riproducibile.
Temperatura centigrada: TC = TK - 273,16
Il grado centigrado può essere definito come la centesima parte tra il punto di fusione del
ghiaccio a pressione atmosferica e la temperatura di ebollizione dell’acqua alla stessa
pressione.
Punto triplo:
TK = 273,16 K TC = 0,01°C
Punto di fusione (1 bar):
TK = 273,15 K TC = 0,00 °C
• CALORE: una forma di ENERGIA (Energia Termica)
Grandezza scalare
Unità di misura di base: J
(joule)
Vecchia unità di misura: kcal
(1 kcal = quantità di calore necessaria per innalzare di 1 °C
- da 14,5 a 15,5 - 1 kg di acqua) 1 kcal = 4.186,8 J = 4,2 kJ (spesso Jt -t = termici-, così
kWht -termici- e kWe -elettrici-)
• CAPACITA’ TERMICA DI UN CORPO o CALORE SCAMBIATO:
Q = Cs x m x (T2 - T1)
(m = massa del corpo in kg)
T2 <=> T1
(Cs = capacità termica massica in J/kgxK)
Per l’acqua Cs = 4,2 kJ/kgxK (0 - 100 °C); acciaio Cs = 0,50 kJ/kgxK; legno Cs 2,42,7 kJ/kgxK; aria (20 °C, 1 bar) Cs = 1,01 kJ/kgxK
• TRASMISSIONE DEL CALORE
Q = U x S x (T2 - T1)
(t = tempo in secondi)
(U = coeff. di trasmissione termica termica di
un corpo con superficie di scambio S)
U = f (λ/l, hc, hr)
λ = conduttività termica di un corpo con spessore (lunghezza) l (W/mxK)
hc = coeff. di scambio convettivo (W/m2xK) (convezione naturale o forzata)
hr = coeff. (linearizzato) di scambio radiativo (W/m2xK)
acqua
acciaio (+Ni)
legno
aria (0 - 100 °C)
(W/m2xK )
0,63
29 - 105
0,10 - 0,27
0,0235 - 0,0306
Per un motore a combustione
interna circa 1/3 del calore
generato dal combustibile è
trasformato in lavoro utile, circa 1/3
è perso con i gas di scarico e un
altro 1/3 deve essere smaltito dal
sistema di raffreddamento (per ogni
kW di potenza meccanica deve
essere smaltito 1 kWt)
TERMODINAMICA
• 1°PRINCIPIO: L’energia (interna) non si crea ne si distrugge, può solo essere
convertita da una forma in un’altra.
Q = ∆U + L
(U = energia interna -variabile di stato-)
Se si riscalda un sistema termodinamico parte del calore serve per aumentare l’energia
interna del corpo (∆U), cioè per aumentare la sua temperatura, parte per compiere un
lavoro.
∆U = Q - L
Q positivo se assorbito dal sistema
L positivo se fatto verso l’esterno
L = p x ∆V = (F/S) x S x ∆l
L’energia può essere definita come la capacità di un sistema di scambiare lavoro
o calore.
TERMODINAMICA
• 2°PRINCIPIO: L’energia meccanica può essere trasformata totalmente in calore, il
calore non può essere trasformato totalmente in energia meccanica.
Ciclo di Carnot e macchina ideale
η =
L
Q − Q2
T -T
T
= 1
= 1 2 = 1- 2
Q1
Q1
T1
T1
T = temperatura assoluta
T2<T1
Massimo rendimento per un motore
termico con temperatura di combustione
di 2.200 °C e T2 = 15 °C (t. ambiente):
ηmax = 1-
15 + 273
= 1- 0,12 = 0,88 → 88%
2200 + 273
η reale per motori diesel: 30 - 40 %
COMBUSTIBILI
• Come fonti energetiche si hanno a disposizione essenzialmente dei
COMBUSTIBILI: penalizzati nella conversione in Energia Meccanica (lavoro utile)
• POTERE CALORIFICO DI UN COMBUSTIBILE:
Potere calorifico inferiore (Pci): nella tecnica è quello più usato; calore svolto in
un processo di combustione completa a pressione costante (atmosferica) dall’unità
di massa di combustibile quando i fumi (gas) di combustione sono raffreddati fino a
100 °C (H2O formato come fase vapore):
CH4 + 2O2
CO2 + 2(H2O)v Pci metano: 48 MJ/kg (8.250 kcal/m3 ; ρ=0,717 kg/m3)
p=100 kPa T=100°C
Pci petrolio greggio: 10.000 kcal/kg = 42 MJ/kg; Pci benzina: 10.500 kcal/kg = 44 MJ/kg;
Pci gasolio: 10.200 kcal/kg = 43 MJ/kg
Potere calorifico superiore (Pcs): quando i gas di combustione sono raffreddati
con fase H2O come liquido:
CO2 + 2(H2O)l Pcs metano: 55 MJ/kg (9.370 kcal/m3)
CH4 + 2O2
p=100 kPa Tr=100°C o (più diffusa) 15°C (temp. di riferimento secondo norma)
Pcs=Pci + mH2O x Ql + mg x csg(100-Tr) + mH2O x csH2O l (100-Tr)
cal.latente
cal.sens. (trascur.)
cal. sensibile
Ql: calore latente di evaporazione dell’acqua a 100 kPa = 539 kcal/kg = 2,26 MJ/kg
csg: calore specifico dei fumi di
combustione (1,01 kJ/kgxK) pari a
quello dell’aria in prima approx.
COMBUSTIBILI
Distillazione frazionata del greggio:
30°C - 200°C: benzine; 180°C - 360°C: gasolio
IDROCARBURI
{
paraffine (o normal-paraffine): catena lineare (CnH2n+2)
isoparaffine: catena lineare ramificata (CnH2n+2)
olefine: catena lineare con doppio legame fra C (CnH2n)
nafteni: catena chiusa (CnH2n)
aromatici: anelli a 6 atomi di C con tre doppi legami (CnH2n-6)
N.O. (numero di ottano): misura il potere antidetonante (maggiore per aromatici)
benzine con Pb NO > 97; benzine senza Pb NO > 95
N.C. (numero di cetano): misura l’accendibilità (maggiore per paraffine)
diesel NC > 48 (empiricamente: NO = 120 - 2NC)
Punto di scorrimento: misura la capacità di scorrere a bassa temperatura (maggiore
per aromatici) (P.d.S. = P.d. solidific. + 3°C)
Indice di viscosità: misura la variazione della viscosità con la temperatura (maggiore
per paraffine)
MOTORE: GRANDEZZE CARATTERISTICHE
PMS = Punto Morto Superiore
PMI = Punto Morto Inferiore
C = Corsa (distanza tra PMS e PMI =
= 2 x raggio manovella)
D = Alesaggio (diametro interno cilindro)
V2 = Camera di compressione
V1/V2 = Rapporto di compressione
V1 – V2 = Cilindrata unitaria
(volume spazzato nella corsa dello
stantuffo)
MOTORE: CICLO DI FUNZIONAMENTO A 4 TEMPI
1
2
1. Aspirazione
2. Compressione/Iniezione
4
3
3. Combustione/Espansione (fase
attiva)
4. Scarico
N.B.: nel motore Diesel la combustione
avviene spontaneamente per
surriscaldamento della miscela aria-gasolio compressa nella camera di
combustione (PV=nRT); nel motore a
benzina l’accensione avviene con l’ausilio
di una scintilla provocata dalla candela.
MOTORE: CICLO DI FUNZIONAMENTO A 4 TEMPI
1
4
2
3
Motosega
Motore a 2 tempi:
1 camera di combustione
2 pistone
3 condotto di scarico
4 condotto di aspirazione
5 carter
6 albero a gomiti
7 canale di alimentazione
8 candela
Aspirazione - compressione
accensione - combustione
espansione
Scarico - completamento
aspirazione
MOTORE: CICLO OTTO E CICLO DIESEL
Otto
ηε=1-(1/rck-1)
rc=6÷10
Diesel ηε=1-(1/rck-1)[(τk-1)/(k(τ-1))]
ηε=Lteor/Q
(rendimento
termodinamico ideale)
rc=14÷22
rc=V1/V2
(rapporto di
compressione)
Lteor>Lind>Leff
τ = V3/V2 = T3/T2 (rapporto di combustione a pressione costante)
k = Cp/Cv ≈ 1,4 (aria)
Lteor = lavoro teorico; Lind = lavoro indicato; Leff = lavoro effettivo (perdite per attrito del pistone nel motore)
ηe = Lteor/Q = rendim. termodinamico ideale; ηi = Lind/Lteor = rendimento indicato; ηm = Leff/Lind = rendim. meccanico
(organico)
ητοτ= Leff/Q = ηe ηi ηm = 1/(cs Pci)
MOTORE: CICLO OTTO E CICLO DIESEL
rc
Grazie a maggiori rapporti di compressione il ciclo Diesel consente rendimenti
termodinamici ideali maggiori rispetto al ciclo Otto. Il ciclo Sabathè è quello
adottato dai motori “Diesel veloci” (quelli che oggi sono impropriamente
chiamati “motori Diesel”).
TURBOCOMPRESSORE
Turbina messa in movimento ad altissima
velocità (superiore a 100.000 giri/min) dai gas di
scarico del motore
+
Compressore centrifugo.
Turbina: fornisce l’energia necessaria al
funzionamento.
Compressore: spinge l’aria prelevata
dall’esterno verso i cilindri.
• Alberino di collegamento tra turbina e
compressore: lavora in bagno d’olio,
senza elementi meccanici volventi
(non sopporterebbero tali regimi di
rotazione senza surriscaldamenti).
• A pari potenza, un motore turbo pesa
dal 20 al 30% in meno di uno
normale.
• Il turbocompressore è particolarmente
indicato per i diesel: scaricano molto
gas anche ai carichi parziali; non
devono abbassare il rapporto di
compressione (non soffrono di
detonazione); hanno i gas di scarico
piuttosto freddi (300÷500°C contro
500÷1000°C dei benzina).
TURBOCOMPRESSORE
TURBOCOMPRESSORE
a: Chiocciola compressore, b: Supporto, c: Corpo centrale,
d: Protezione termica, e: Chioccola turbina, f: Turbina, g: Uscita
gas scarico, h: Wastegate, i: Ingresso gas scarico, j: Scarico olio,
k: Sede boccola, l: Sede boccola, m: Guida in grafite, n:
Compressore, o: Attuatore wastegate, p: Ingresso aria, q: Tubo
attuatore, r: Diffusore, s: Chiocciola compressore, t: Ingresso olio,
u: Uscita compressore.
MOTORE: CURVE CARATTERISTICHE
f
A: Curva di coppia (curva
B: Curva di potenza (curva
(M)
kW
(P)
(cs)
rpm = round per minute (giri al minuto)
(ω)
derivata: P = Mω = M(2πn/60) )
C: Curva del consumo
specifico (curva rilevata)
“Mappa dei
consumi” o
“Piano
quotato dei
consumi”:
curve di
isoconsumo
specifico
% della coppia di potenza massima
g/kWh
rilevata al banco prova con freno
dinamometrico)
della potenza max
% del regime di potenza massima
MOTORE: CURVE CARATTERISTICHE
MOTORE: RISERVA DI COPPIA e STANDARD DI PROVA
(Pmax)
Parte stabile della curva della coppia
(quella con ramo decrescente con ω)
Curva della potenza
(Cmax)
Riserva di coppia =
= (Cmax – CPmax) / CPmax
(≈ 20%)
(CPmax)
Indice di elasticità =
=(Cmax/CPmax)x(NPmax/NCmax )
(≈ 1,5)
(NCmax)
(NPmax)
Standard di prova:
Fendt
Serie
Favorit
(CV)
SAE (Society of Automotive Engineers)
DIN (Deutsche Industrie Normen)
SAE
141
164
186
209
DIN
125
145
165
185
CV SAE/
CV DIN
1,13
1,13
1,13
1,13
MOTORE: FORMULE RELATIVE ALLA POTENZA
M = coppia erogata (Nm)
ω = velocità angolare (rad/s)
n = n.giri albero motore (giri/min)
P = M·ω = M·(2πn/60)
L = pe·V
P = L·(n/(60·c)) = pe·V·(n/(60·c))
L = ηt·Q
P = ηt·Q·(n/(60·c))
L = lavoro efficace (J)
P = potenza efficace (W)
V = cilindrata (m3)
pe = pressione media efficace (Pa)
c = costante (2 nei motori 4 tempi -> una fase utile
ogni 2 giri albero motore; 1 nei motori 2 tempi)
ηt = rendimento totale = ηe ηi ηm
Q = quantità di calore impiegata in un ciclo
(massa di combustibile bruciata per il suo potere
calorifico in J)
Da si può esplicitare Q in funzione della cilindrata. Si ottiene:
P = ηt ηv s V Pci’ (n/(60 c))
ηv = rendimento volumetrico ( meff/mteor = (ρeff V)/(ρteor/V) ) (ρ = massa volumica funzione di p e T)
s = rapporto di sovralimentazione in massa ( mteor/m0 = (ρteor V)/(ρ0 V) )
Pci’ = tonalità termica della miscela (J/m3) (= ρ0 Pci) (Pci = potere calorifico della miscela (J/kg))
meff = massa effettiva di miscela che riempie i cilindri; mteor = massa teorica di miscela che dovrebbe riempire i cilindri
alle condizioni di mandata e aspirazione; m0 = massa “normale” di miscela a condizioni “normali” (15°C e 100 kPa)
(che dovrebbe riempire i cilindri)